基于节水条件的邯郸市工业需水预测

夏 锋，索梅芹，王一杰，王丽丽

(河北工程大学 水利水电学院，河北 邯郸 056038)

2018年邯郸市人均用水量为1.98×102m3，按国际公认标准，属极度缺水地区，而邯郸市工业发展起步较早、速度较快，平均每年工业需水量在2.30×108m3以上，耗水量较大，使得邯郸市本就矛盾的水资源供需关系更加突出。工业需水量预测对于地区的未来发展与规划极其重要，但有关邯郸市工业需水预测方面的研究很少。因此，为保障行业用水需求与地区的可持续发展，邯郸市的工业需水量亟需科学有效地预测。

工业需水量预测需考虑工业产值、产业结构、工业重复水利用率、节水程度、工业政策以及工业的发展程度等多方面因素，工业需水量依据其中内部因素而千变万化，因此，将所有的影响因素建立相关关系以预测需水量非常困难。1982年，邓聚龙[1]创立了灰色系统理论，为解决数据少、贫信息不确定性问题提供了新思路，其中GM(1,1)模型成为应用最广泛的灰色模型。2012年，甘月云等[2]运用灰色GM(1,1)模型预测围场县城镇生活需水量，证明该模型预测结果较为理想；2013年，孙晓红等[3]针对常规GM(1,1)模型的不足，建立等维灰色GM(1,1)模型以提高模型精度，并将其应用于2A12铝板材疲劳寿命的预测，结果表明等维灰色GM(1,1)模型比常规GM(1,1)模型预测结果更加接近实际，对于中长期的预测也更为精准，模型精度也更高；2014年，郭兰兰等[4]将残差修正GM(1,1)模型应用于水质预测中，证明在较为离散的序列下，残差修正GM(1,1)模型的预测精度明显高于传统GM(1,1)模型；2019年，刘雁灵等[5]利用新陈代谢GM(1,1)模型对中国病毒性肝炎发病率进行预测，结果表明，新陈代谢GM(1,1)模型较GM(1,1)模型预测精度较高。总而言之，GM(1,1)模型在处理数据少、贫信息不确定性问题上有较好表现，但在处理较离散序列、预测远端数据时略显乏力，而残差修正GM(1,1)模型与等维递补理论则可以很好地弥补这些不足。由于邯郸市各区域历年工业需水量数据序列较为离散，直接采用GM(1,1)模型相对误差较大且精度低，结果不理想，故本文以GM(1,1)模型为基础，引入残差修正GM(1,1)模型以及等维递补理论，对邯郸市工业需水量进行预测，以弥补邯郸市地区工业需水预测研究不足的现状。

此外，河北省水利厅办公室于2020年9月14日印发的《关于下达“十四五”期间节水主要指标的通知》规定了邯郸市2025年万元工业增加值用水量指标[6]，本文将基于此文件，计算邯郸市2025年工业节水潜力，并对工业需水量预测值校正，进一步提升预测值的准确性。

1 研究方法

本文基于2009—2019年邯郸市工业用水量，运用MATLAB(R2018a)软件构建GM(1,1)模型、残差修正GM(1,1)模型与等维递补残差修正GM(1,1)模型，确定模型维数并比较模型精度，对邯郸市2025年的工业需水量进行预测。

1.1 GM(1,1)灰色模型及其残差修正

灰色模型通过累加生成变换进行序列数据建模，把原始数据序列不明显的变化趋势通过累加变换后呈现明显的趋势，并用灰色差分方程和灰色微分方程对变换后的数据进行建模，最后用累减生成的序列进行数据模拟和预测[7]。

GM(1,1)灰色模型原理如下。

设用水量原始数据序列为：

X(0)= (x(0)(1),x(0)(2),…,x(0)(m))

(1)

其中x(0)(n)对应的是按时间顺序排序的第n年实际用水量，下同。

将x各项进行累加得到序列：

X(1)=(x(1)(1),x(1)(2),…,x(1)(m))

(2)

其中：

(3)

求出累加序列X(1)的平均值T，序列T又称X(1)的均值生成序列或系统的背景值。

T(1)=(t(1)(2),t(1)(3),…,t(1)(m))

(4)

其中：

(5)

则称式(6)为一阶单变量灰色预测模型，又称GM(1,1)模型。

x(0)(k) +at(0)(k) =u

(6)

其中，参数a是主变量参数，u为GM(1,1)模型的灰作用系数或者背景值。a、u的值可通过最小二乘法确定。

根据求出的a、u值，可以得到灰色模型的预测方程为：

(7)

通过式(3)可以求出一次累加生成序列的模拟值,将各项累减得到原始数据的模拟值。

对模拟值进行检验，若通过检验，则可以运用式(8)对用水量进行预测。

(8)

模型检验是模型投入使用前的最后一步。对于灰色模型而言，通常采用的是后验差检验。后验差检验的两个主要指标为方差比C和小误差概率P。方差比C值越小，预测效果越好；小误差概率P值越高，则预测精度越高。进行后验差的步骤如下[8]。

步骤一首先求出原始数据的残差：

残差q(k)的计算公式为：

(9)

步骤二计算原始数据序列和残差的均值：

(10)

(11)

步骤三计算原始数据序列和残差的方差：

(12)

(13)

步骤四计算方差比C和小误差概率P：

(14)

(15)

步骤五对照模型精度评价(表1)[4]，对计算出的C、P值进行判断。

对邯郸市各区域历年工业用水量建立GM(1,1)模型，进行后验差检验，仅广平县和临漳县评价结果为“好”，对于其他区域则采用残差修正模型对GM(1,1)模型进行修正。残差修正GM(1,1)模型的原理为：由于实测数据序列存在一定的规律，可通过灰色模型发现这种规律并得到预测值，那么预测值与实际值之间必然有一些误差属于系统真实序列，同样可以通过GM(1,1)模型进行预测[9]。当数据不确定性较强或数据波动较大时，可以利用q(k)建立残差序列建立GM(1,1)模型，利用残差模拟值调整原始数据，从而使预测结果变得更为合理精确。残差修正最关键的是确定k≥n时残差预测值的符号。一般采用马尔可夫过程推求残差正、负号状态转移概率，通过建立状态转移矩阵来计算第k年出现正负号的概率，从而确定残差预测值的符号[10]。对经过残差修正后的预测结果进行检验，计算C、P值。

1.2 等维递补残差修正GM(1,1)模型

在传统的残差修正GM(1,1)模型中，由于数据的不同，得到的预测值也不尽相同，预测值的上界与下界中的区域为预测值的灰色区间，并且随着预测序列的延长，灰色区间也会随之变大[8]。为减少灰色预测值范围，最有效的方法就是剔除最原始数据，同时加入残差修正GM(1,1)模型预测出来的一个最新数据[11]。

采用等维递补预测的建模方式就是在过去n年数据序列中选取连续的t年数据建立残差修正GM(1,1)模型，预测出t+1年数据，然后去掉初始序列中的第一个数据，加入t+1年数据，重复建立残差修正GM(1,1)模型，依次类推。

1.3 节水修正值

本文基于河北省下发的相关文件中所规定的万元工业增加值用水量，对比应用等维递补残差修正GM(1,1)模型预测所得规划年万元工业增加值用水量，计算规划年修正值，并用以修正预测值。

节水修正值计算公式如下[12]：

(16)

式中R——节水修正值；I——使用上述模型计算所得出的各县区规划年工业需水量,104m3；Y1——使用此模型得到的规划年万元工业增加值用水量，m3/万元；Y2——上述文件中规定的规划年万元工业增加值用水量，m3/万元。

2 基于节水条件的邯郸市工业需水量预测

工业需水量变化情况受多种因素影响，其中节水程度占一定比重。确定邯郸市不同地区应用的模型维数并比较残差修正GM(1,1)模型与等维递补残差修正GM(1,1)模型精度，基于邯郸市各区域2009—2019年工业用水量[13]与邯郸市2009—2018年工业增加值[14]，预测2025年邯郸市各区域工业用水量与邯郸市万元工业增加值用水量，根据式(16)计算邯郸市2025年工业节水修正值。结合预测值与节水修正值，得2025年邯郸市工业需水量最终预测值。

2.1 维数确定

对修正后的各县区的数据序列进行方差比C和小误差概率P检验，均通过检验。其中，大名县、邱县、肥乡区、磁县及馆陶县验证结果为“勉强”；临漳县和武安市验证结果为“好”；其他区域均为“合格”。因此，可以运用等维递补残差修正GM(1,1)模型建模预测。但是，GM(1,1)模型最少只需要4个数据就可进行预测，并非是数据越多，预测就越准确[15]。为提高其精度及预测的准确定，选取不同维数的数据建模，比较其基础模型精度及相对误差，从中选取拟合效果最佳的模型维数进行预测，表2—4为邯郸市东、中、西部3个典型县区的维数确定情况。

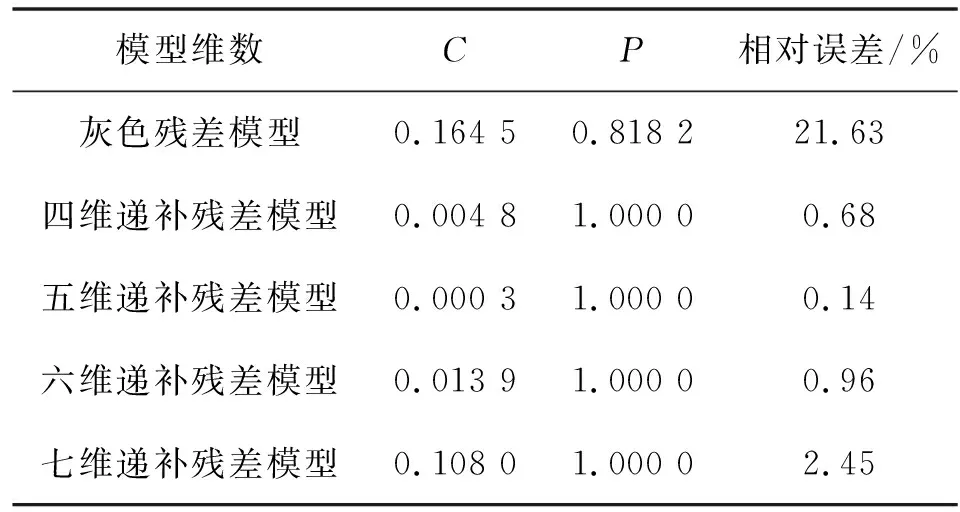
表2 馆陶县不同维数下残差修正GM(1,1)模型精度检验

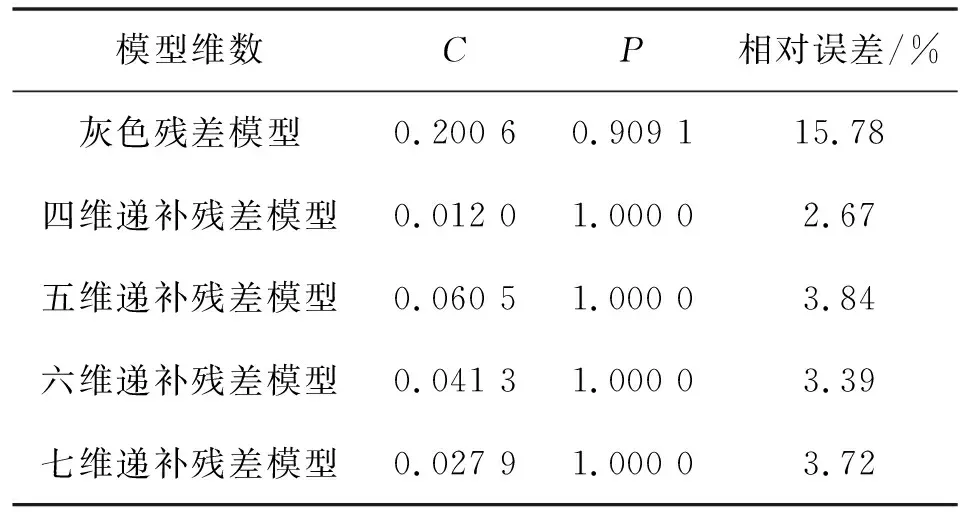
表3 永年区不同维数下残差修正GM(1,1)模型精度检验

表4 涉县不同维数下残差修正GM(1,1)模型精度检验

由表1、2、3，可知馆陶县在运用五维递补残差修正GM(1,1)模型的情况下精度最好，相对误差最小，而永年区和涉县则在使用四维递补残差修正GM(1,1)模型计算的情况下精度最好。因此，对于不同县区，应使用不同维数的等维递补残差修正GM(1,1)模型进行计算。

2.2 精度验证

对邯郸市各县(区)2009—2017年工业用水量序列分别建立上述3种模型，预测2018—2019年工业需水量，计算节水修正值，将节水修正值用以修正结果，进而计算得出2018—2019年预测结果与真实值序列之间的相对误差，结果见图1。

图1 相对误差比较情况

相对误差平均值(J)计算公式如下：

(17)

(18)

其中，大名县、邱县、肥乡区、磁县及馆陶县均未通过后验差检验值，C值均大于0.8，表示GM(1,1)模型不适用于这5个地区。

2017年，邯郸市大力倡导相关企业进行技术改造，提升企业装备水平，淘汰落后产能，不断优化经济结构。2018年，新增入驻企业30多家，展开众多项目推动工业发展。由于一系列政策的实施，邯郸市在2018—2019年工业发展迅速，行业用水量变化较大，其中，大名县、邱县、肥乡区、磁县与馆陶县变化情况尤为强烈。因此，2018—2019年3种模型预测结果与实际值偏差较大，在此情况下，提升预测精度，将平均相对误差降低至20.0%以下，使得区域在优化产业结构同时，依旧能够得到较为精准的需水量数据，为区域的未来发展提供理论支撑。

从图1可知，GM(1,1)模型的平均相对误差为54.0%；残差修正GM(1,1)模型的平均相对误差为32.6%；等维递补残差修正GM(1,1)模型中80%模拟值的相对误差较残差修正GM(1,1)模型而言要小，总体序列相对误差仅为20.1%。纵然邯郸市近年来工业需水量情况变化剧烈，等维递补残差修正GM(1,1)模型在大多数县(区)依旧取得了良好的预测效果。在此基础上计算节水修正值并用以修正模型预测值，使得预测值相对真实值误差进一步减少了4.0%，全市各县(区)平均相对误差仅为16.1%。显然，运用等维递补残差修正GM(1,1)模型结合节水修正值得出的预测结果更为合理。

2.3 基于节水条件的工业需水量预测

基于邯郸市历年万元工业增加值用水量情况，运用等维递补残差修正GM(1,1)模型对邯郸市2025年万元工业增加值用水量进行预测，对比河北省水利厅颁发的《关于下达“十四五”期间节水主要指标的通知》中对邯郸市2025年万元工业增加值用水量的规定，计算相应差值。而后将其与用上述模型计算所得的工业需水量预测值结合，得出邯郸市2025年各区域工业需水量的最终预测值。

邯郸市基于节水条件的工业需水量预测值见表5。

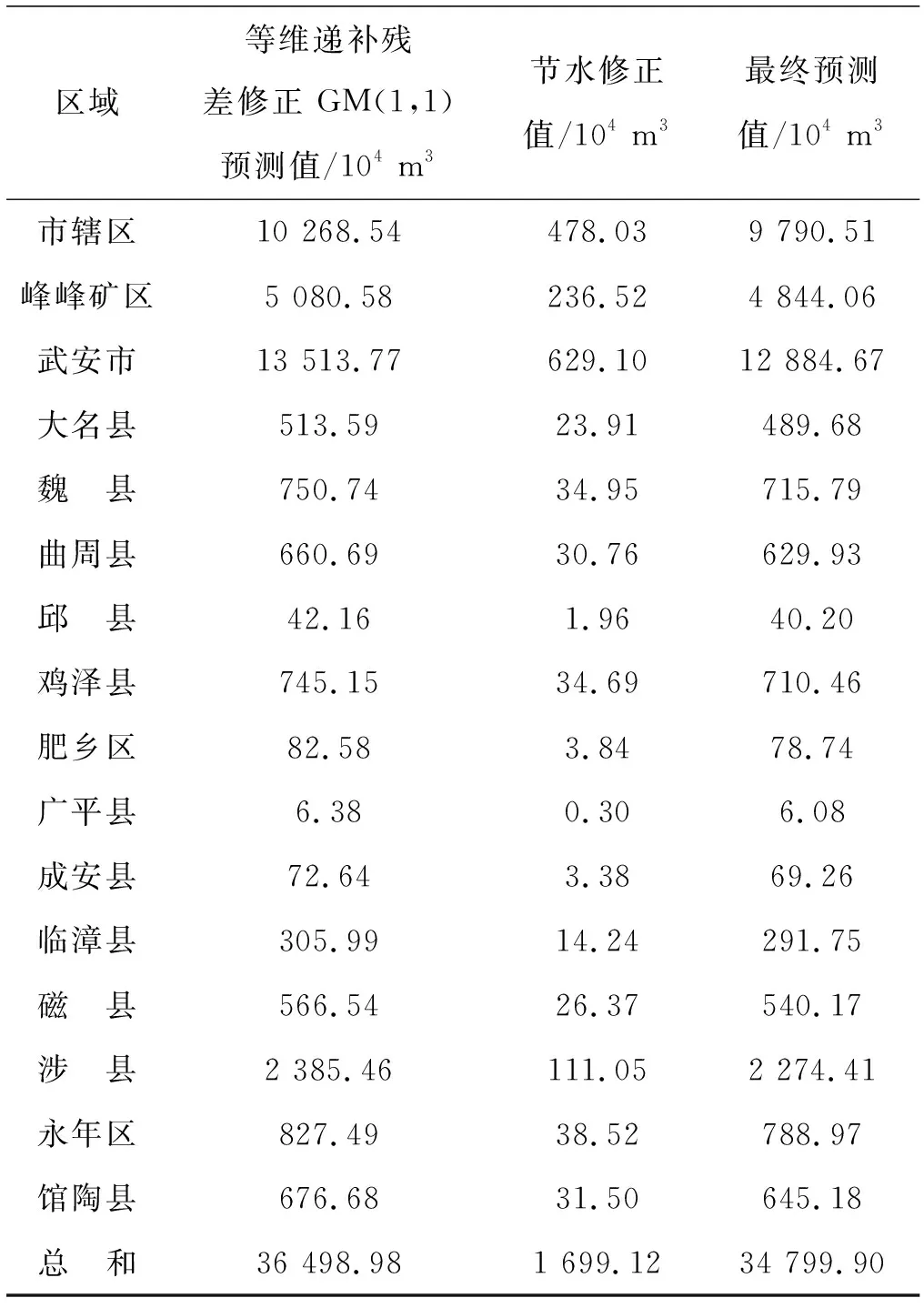
表5 2025年邯郸市工业需水量

由表5知，基于等维递补残差修正GM(1,1)模型预测得到2025年邯郸市工业需水量为36 498.98×104m3，根据式(16)得到2025年邯郸市工业节水潜力为1 699.12×104m3，结合模型预测值与工业节水修正值，得邯郸市2025年工业需水量为34 799.90×104m3。从结果可知，未来几年内，随着经济的持续发展与工业转型期的平稳度过，邯郸市需水量会呈增加趋势，且发展速度较近几年而言会更加迅速。

3 结论

a)由于邯郸市工业用水量影响因素较多，序列较为离散，直接采用GM(1,1)模型预测不能取得较好的结果。残差修正GM(1,1)模型在一定程度上能修正误差，但对远端数据的预测能力依旧较弱。等维递补残差修正GM(1,1)模型通过动态预测的过程，弥补了残差修正GM(1,1)模型的缺点。由上文所述可知，等维递补残差修正GM(1,1)模型较GM(1,1)模型与残差修正GM(1,1)模型而言，相对误差分别减少了33.9%、12.5%，更适用于邯郸市工业需水量预测，预测精度更高，预测结果更为精准。

b)本文在运用等维递补残差修正GM(1,1)模型计算邯郸市规划年工业需水量的基础上，还考虑了此灰色系统中万元工业增加值用水量的变化趋势，结合河北省规定的规划年邯郸市万元工业增加值用水量，计算邯郸市节水修正值。在已有计算结果上进行节水修正，使得预测结果更为准确。

c)本文基于等维递补残差修正GM(1,1)模型预测得到2025年邯郸市工业需水量为36 498.98×104m3；此外，计算邯郸市2025年工业节水修正值为1 699.12×104m3。结合两部分计算结果，得邯郸市2025年工业需水量为34 799.90×104m3。此结果表明，随着经济发展与工业转型发展，邯郸市工业需水量依旧会呈持续增长的状态。