航天器集群控制与规划算法仿真验证平台设计*
2021-11-24夏红伟马广程李旭东孙浩然马长波
高 雅,夏红伟,马广程,李旭东,孙浩然,马长波
(1.哈尔滨工业大学 航天学院· 哈尔滨·150001;2.上海航天控制技术研究所·上海·201109)
0 引 言
随着空间技术的发展,一些复杂的应用场景,比如太空中太阳能电池板等大型设备的组装,已经不能依靠单个航天器来完成,多航天器协同逐渐成为了解决这类空间任务的一种有效途径[1]。航天器集群作为一种新兴的多航天器协同模式,已经成为了分布式空间系统的重要研究方向。近些年来,针对智能集群的理论研究取得了巨大的进展,如人工势场法[2]、模糊思想[3]、仿生行为分析[4]等。然而,为验证集群智能算法的可行性与正确性,仅进行数学仿真是不够的,还需要通过全物理仿真试验来复现系统所处的真实环境,模拟真实的噪声、扰动等不确定因素。
气浮模拟器系统是一种航天器集群地面仿真试验平台,该平台可以为航天器集群控制算法的可行性与正确性提供一种有效的模拟、评测环境和手段。以色列工学院的分布式空间系统实验室设计了一个用于测试卫星集群飞行技术的试验平台,在通过3D打印生产的气浮机器人上配置了惯性单元、执行机构和控制器等设备,实现了集群行为的全物理仿真;由美国加利福尼亚理工学院喷气推进实验室开发的编队控制模拟器,包括了两套五自由度的模拟系统,模拟器上装有星敏感器、光纤陀螺、反作用轮、冷气体推进器以及嵌入式计算机,用于论证航天器集群的制导、控制算法、参数估计等[5]。在国内,以哈尔滨工业大学、中国科学院大学、北京控制工程研究所等为代表的机构,在气浮模拟器的研制方面取得了不俗的成果。但与国外相比,气浮模拟器技术在航天器集群的全物理仿真系统方面的应用较少。
在这种背景下,从理论和工程实践两方面考虑,本文设计了一种基于气浮技术的航天器集群控制与规划算法仿真验证平台,该平台可以在地面上实现集群导航、规划与控制算法的全物理分析与验证。最后,给出了一种基于滑模控制的集群路径规划算法,并通过仿真,验证了算法的有效性。
1 仿真验证系统的总体方案设计
1.1 位姿识别方案设计
航天器集群系统在外太空工作时,大多采用图像识别或惯性测量的位姿识别方式,并通过无线数据传输使每个成员均可获得其余成员的位姿信息。在航天器集群控制技术的仿真验证系统中,参考真实航天器集群在轨工作时的位姿识别方式,为了便于进行地面试验,可以考虑以下三种位姿识别方案:
(1)基于惯性组合的位姿识别装置
惯性组合具有实时性好、抗干扰能力强、不受气象条件限制等优点,因此常可被用于姿态测量和导航等应用领域。在仿真试验系统内的每个成员上安装包含陀螺和加速度计在内的惯性组合,测量成员在x、y方向的平动状态和绕竖直轴的转动状态,并利用卡尔曼滤波算法对测量数据进行处理,以获得成员的高精度位姿信息。
(2)基于双目视觉的相对位姿识别装置
采用图像测量的方式进行位姿识别,可以避免由传统惯组带来的漂移误差,确保长时间工作时的导航精度保持不变。双目相机安装在集群内的每一个成员上,基于计算机视觉,通过顶部正中央的靶标实时识别并获得相邻成员的位姿信息,同时与其他成员进行通信,其效果如图1所示。

图1 基于双目视觉的位姿测量装置的识别效果图Fig.1 Recognition effect diagram of pose measurement device based on binocular vision
(3)基于单目视觉的全局位姿识别装置
惯组和双目视觉相机的测量范围有限。在集群导航定位过程中,每个成员需要实时地与其他成员交换位姿信息,这导致网络负载较大。安装在集群正上方的单目相机采用了全局测量方案,以每个成员顶部的靶标为参照物,可实现对集群内所有机器人的位姿测量。
本文提出的航天器集群控制技术仿真验证系统的第一代产品选用了第三种位姿识别方案,通过支撑架将单目相机固定在了实验平台的正上方;安装在机器人顶部正中央的靶标图像经二值化处理后的结果如图2所示,相机通过靶标中的三个标志点的相对位置信息来区分和识别集群内的每个成员。其中,最外层的黑色圆形标志点质心记作Z,内含的3个白色圆形标志点质心组成了三角形ABC。三角形的最长边为AB,与之相对的顶点为C,次长边为AC,与之相对的顶点为B,最短边为BC,与之相对的顶点为A。首先,以整张测试图片为目标区域,以黑色为前景色,白色为背景色,提取轮廓,并求解质心和轮廓半径,可求得Z点的坐标与对应标志点的外接矩形。随后,以标志点Z的外接矩形为目标区域,以白色为前景色,黑色为背景色,提取轮廓,并求解质心,可以得到3个白色标志点的质心坐标。其中,A、B两点的坐标可用于进一步对待测目标的位姿进行计算,C点可用于待测目标之间的区分。相机识别靶标,并通过AB的长度以及C到AB中点的距离完成多个目标的区分。

图2 二值化后的靶标图像Fig.2 Target image after binarization
整个测姿定位过程主要可分为四个环节,相机标定、图像采集、特征提取,以及目标检测并输出结果。图像采集开始之前,需要进行相机标定,建立相机的针孔成像模型,以便于后续的位姿坐标变换;相机标定完成后,通过图像采集得到被测靶标的图像,根据工作距离、成像范围等要求,设置合适的曝光时间、调节光圈及焦距,采集出成像效果最佳的靶标图像;然后,在指定区域生成模板图像,定位出模板图像的中心(参考点),并圈定所拍摄图像的搜索区域,进行靶标图像的特征提取,得到标志点的位置坐标;最后,进行目标检测并输出结果。根据由特征提取得到的标志点坐标,将通过相机标定得到的数据进行坐标变换,并通过运算得到真实坐标系下的位姿信息。根据既定的判定条件,判定本次测姿定位数据是否可靠,位姿信息将按照设计的通信协议、通过UDP发送到每个成员的控制器上。
1.2 仿真验证系统的组成
仿真实验系统由平台支撑分系统、台上气浮机器人、位姿识别分系统和台下监控分系统构成,系统组成如图3所示。由光滑大理石平台构成的平台支撑分系统为集群内的气浮机器人提供了工作模拟环境;气浮机器人底部的气足产生高压气膜,使其悬浮在大理石平台上,可模拟航天器在外太空中的微阻尼动力学环境;位姿识别系统采用全局图像测量的位姿检测方式,并通过UDP将集群内所有成员的位姿信息传输给每个气浮机器人的控制器;演示系统配有台下监控分系统。通过友好的人机交互界面,使用户在台下能够实时监控集群的运动状态。
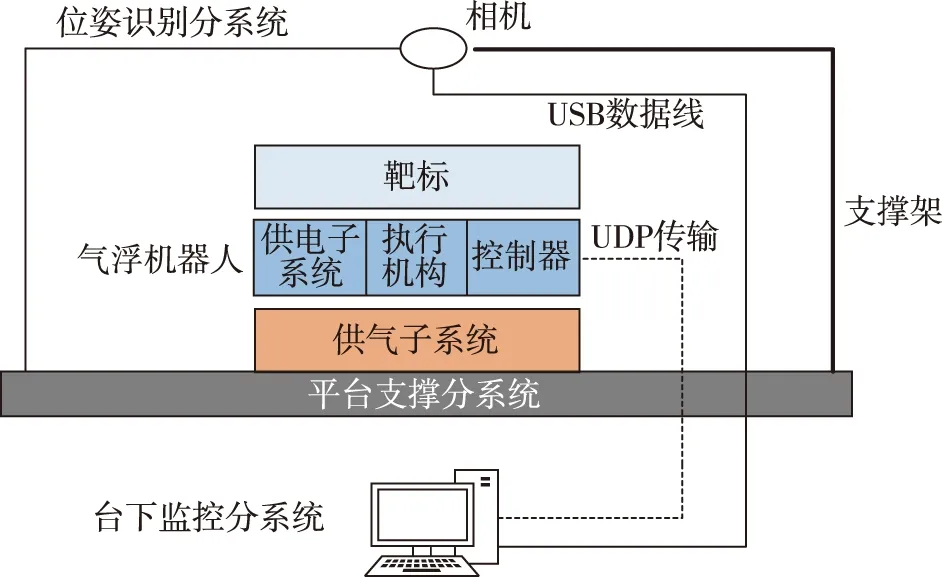
图3 仿真试验系统组成示意图Fig.3 Schematic diagram of the demonstration system
气浮机器人是整个演示系统的核心,其包括供电子系统、供气子系统、控制器、执行机构等设备,采用了层次式结构,将机器人上的相关设备进行了分层放置,使得布局更加合理、清晰。在系统工作的过程中,大理石平台正上方的单目相机通过安装于集群内每个机器人表面的靶标来区分不同的成员,并将每个成员的位姿数据通过USB数据线传输给台下由配套工控机组成的监控分系统。监控分系统通过人机交互界面实时显示每台机器人的位姿数据。用户在界面上输入集群内每个成员的期望位姿信息,每个机器人上的控制器通过UDP接收集群内所有成员的位姿信息,再根据设计的路径规划算法求解出控制量。应用力矩分配算法,控制器将控制量分配到每个执行机构上。最后,通过串口将每个执行机构的控制量输出给驱动板。驱动板将控制信号转换为PWM信号,以驱动执行机构,控制过程如图4所示。演示系统通过4个微型风扇驱动气浮机器人到达指定的位置和姿态,以实现航天器集群编队的全物理仿真。风扇的安装示意图如图5所示。

图4 控制过程示意图Fig.4 Schematic diagram of control process
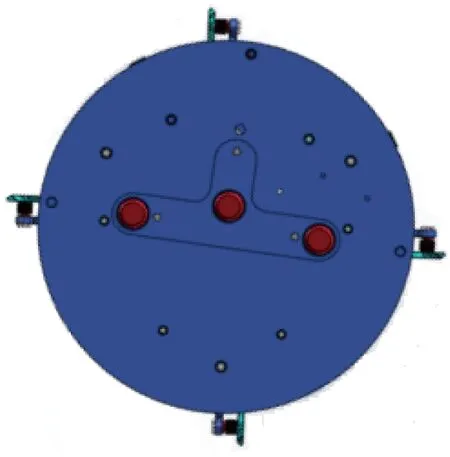
图5 风扇安装位置示意图Fig.5 Schematic diagram of the fan installation position
2 基于行为的集群运动场模型
演示系统内的集群成员都是平等且独立的。同时,通过上文论述的全局图像识别技术,每个成员都可以准确地获得其余成员的位姿信息。本文参考Izzo和Pettazzi在文献[6]中提出的一种基于行为的集群运动场建模方法,即设计集群内成员的多种行为函数,通过设置相应的权重系数,将集群的运动场定义为不同行为的贡献之和。这种方法从集群期望的编队配置出发,通过计算实现了最终配置时每个成员的期望速度。
假设集群内有n个成员,每个成员的平衡位置为ξi,当前位置和速度分别为xi和vi,i=1,…,n。集群内每个成员受到的作用力可以分解为目标位置对成员的吸引力和障碍物(集群内其余成员和大理石平台边界)对成员的排斥力[7]。因此,由作用力产生的行为包括向目标位置运动的聚集行为和躲避障碍物的排斥行为。下面,给出两种行为的具体定义函数。
(1)聚集行为
聚集行为表示目标位置对成员的吸引效果,聚集行为将使得集群内的每个成员向着目标位置移动,可定义行为函数如下
(1)
(2)回避行为
回避行为表示障碍物对成员的排斥效果,如图6所示。当成员在远离平台边界的区域(区域Ⅱ)内运动时,仅考虑成员与其他成员之间避免碰撞

图6 回避行为的作用区域示意图Fig.6 Schematic diagram of the area of action of avoidance behavior
(2)
其中,整数bi表示排斥效果的强度,ka,i表示成员间排斥力的影响范围。
当成员在靠近平台边界的区域(区域Ⅰ)内时,需要将边界视为障碍物
(3)
式中,d0表示平台边界对成员的排斥效果的作用范围,即区域Ⅰ的宽度,dj表示成员到边界的距离。回避行为的效果强度与成员到障碍物的距离负相关,且具有局部效应。
集群内每个机器人的期望速度是以上两种行为的加权和
(4)

vi(x=ξ,λ)=0
(5)
其中,x=[xi…xn]T,ξ=[ξ1…ξn]T。当给定范围参数ka,i、kd,i、d0和一些强度参数时,可以求出剩余参数。
3 滑模变结构控制算法设计与仿真验证
路径规划一直都是智能集群控制领域研究的重点问题[8]。通过给定一系列初始条件和约束条件,在有效躲避障碍物和避免集群内成员相互碰撞的前提下,可自主地、实时地为每个成员规划其到达目标位置的满意路径[9-10]。综合目前该领域中的研究成果[11-12],本文根据上一节推导的行为函数模型设计了一种基于滑模控制思想的路径规划算法。算法结构简单、鲁棒性高[13],能够快速有效地规划出每个成员的运动路径,同时针对传统滑模控制中存在的震颤问题,用一个连续函数代替了滑模控制中的开关函数,最后的仿真结果证明了路径规划算法的可行性。
3.1 基于滑模控制的路径规划算法设计
由于集群内每个成员平等独立且具有结构相同的控制器,下面可省略下标i。航天器集群在大理石平台上运动时,可仅考虑执行机构产生的驱动力和外界扰动力。因此,给出以下形式的集群运动模型
(6)
其中,v是成员运动速度,aN是未建模的扰动加速度,u是控制量。
滑模面及运动示意图如图7所示,每个成员的运动可以分为两个阶段:阶段A使成员的运动状态从初始速度v0逐渐收敛至滑模轨迹,并始终保持在滑模轨迹上;阶段B使成员的运动状态沿着设计的滑模轨迹s=0达到平衡的目标位置,即实现设计的期望速度vd。

图7 滑模面及运动示意图Fig.7 Schematic diagram of sliding surface and movement
首先,需要给出滑模轨迹在控制系统中的实际物理意义。为了使集群实现设计的平衡状态,本文给出了以下形式的滑模面函数
s=vd-v
(7)
其中,vd是给定的三种行为,即式(3)的定义。s=0能够保证成员的速度最终达到设计的期望速度vd。当系统状态到达滑模轨迹s后,为了使其始终保持在s轨迹上,需要满足以下关系
(8)
将式(6)代入式(8),则有
(9)
由此,可以得到滑模控制律中的等效控制部分
(10)
ueq使系统的运动状态与滑模轨迹相交后不再离开滑模轨迹,并逐渐收敛到稳定的目标位置;为了驱动系统的运动状态轨迹与滑模轨迹相交,需要在s<0或s>0的情况下引入切换控制uvss,迫使系统状态向滑模轨迹趋近,并提高系统的鲁棒性。因此,完整的控制律为
u=ueq+uvss
(11)
下面,通过李雅普诺夫稳定性分析的方法来确定uvss。在实际集群系统中,由于每个成员的初始运动状态可能位于状态空间中的任意位置,要求滑模轨迹对于整个状态空间而言具有全局吸引力,即滑模轨迹需要满足李雅普诺夫形式的全局到达条件
(12-1)
(12-2)
将式(6)和式(11)代入式(12-2)中,则有,(vd-v)(uvss-aN)>0,即有
s(uvss-aN)>0
(13)
滑模控制理论并没有对系统状态的趋近运动轨迹做出限制,只需保证状态最终能够收敛到滑模面即可。因此,任何满足该条件的uvss均可驱动系统状态向滑模轨迹运动。本文采用趋近律对uvss的切换控制进行设计。查阅文献[14-15],可选择以下形式的趋近律
uvss=u0sign(s)
(14)
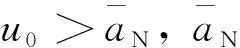
在实际仿真时发现,符号函数sign(s)的不连续性会导致成员在平衡位置附近产生不必要的震颤现象,如图8所示。为了在实现控制目标的前提下消除控制器的不连续性,本文采用平滑且连续的双曲正切函数tanh(γs)来近似符号函数sign(s)。其中,γ表示函数在s=0处的斜率。近似后的控制器大大消除了系统震颤,减少了系统磨损,延长了使用寿命,如图9所示。

图8 滑模控制的震颤现象Fig.8 Chattering phenomenon of sliding mode control
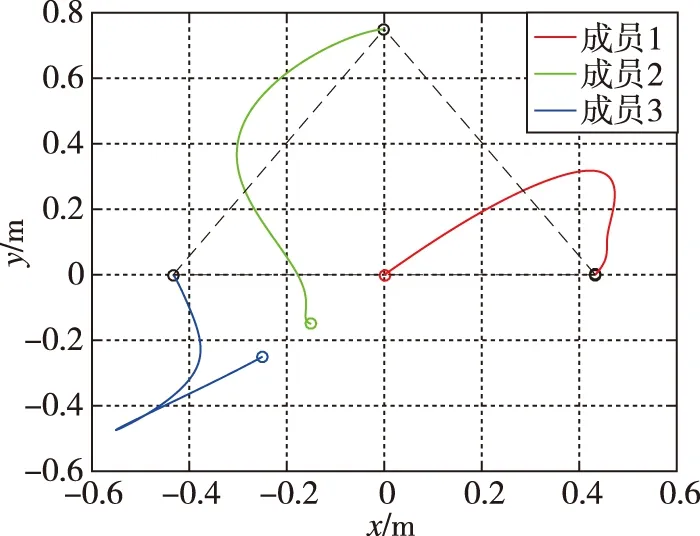
图9 改进滑模控制的仿真结果Fig.9 Simulation results of improved sliding mode control
综上,本文采用的滑模控制律如下
(15)
3.2 仿真实例及结果分析
本文分别针对包含两个成员、三个成员和四个成员的集群编队设计了期望达到的目标队形,根据上文提出的运动场行为函数和路径规划算法,设置u0=10,γ=5,并进行了仿真。仿真结果如图10、图11、图12所示。图10中的两个成员最终到达两个竖直距离为1m的目标位置;图11中

图10 两个成员的集群编队仿真结果Fig.10 Simulation results of cluster formation of two members
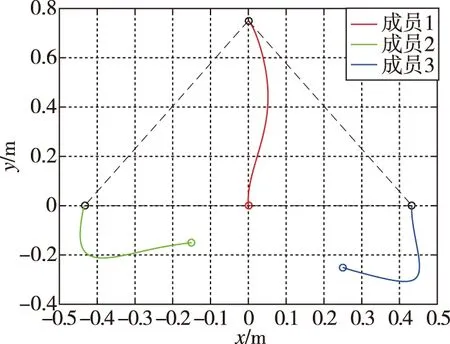
图11 三个成员的集群编队仿真结果Fig.11 Simulation results of cluster formation of three members

图12 四个成员的集群编队仿真结果Fig.12 Simulation results of cluster formation of three members
4 结 论
本文提出了一种基于气浮技术的航天器集群控制与规划算法仿真验证平台的总体设计方案。基于单目位姿识别系统,该仿真验证平台可以实现对所有成员的位姿的全局测量。通过为集群定义“聚集”和“回避”两种行为,建立了基于行为函数的集群运动场模型,设计了一种基于滑模控制算法的路径规划算法,并针对算法中存在的抖振现象做出了改进,最后通过仿真验证了本文方法的有效性。
