基于最优控制的高超螺旋俯冲轨迹设计*

乔毅涛, 耿飞龙，张 新，李 爽

(南京航空航天大学 航天学院·南京·211106)

0 引 言

作为航空与航天领域结合的代表，近年来，高超声速技术在超燃冲压发动机技术[1]取得突破的基础上，也取得了极大的发展。以其为典型应用的高超声速导弹更是以纵深穿透能力、精确打击能力、快速机动能力被各军事强国奉为“颠覆性的存在”。无疑，在高超声速技术领域，美国和俄罗斯走在了世界的前列[2]，而我国则紧随其后。但是，军事技术发展的内在基本矛盾，是进攻与防御的矛盾。一种进攻性武器的出现，必然或迟早会导致相应防御措施的产生，高超声速攻防技术的发展也不例外。为了应对由高超声速导弹带来的威胁与挑战，俄罗斯在反导技术领域也取得了极大的突破[3]。本文正是在高超攻防时代到来的背景下、研究高超声速飞行器在俯冲阶段所面临的防空反导的威胁时，提出了利用末端螺旋机动的形式突破敌方防御，完成打击任务。

郦苏丹等[4]在国内首先提出了弹头再入末端螺旋机动的概念，其文章分析了再入螺旋机动产生的原理，即将弹头设计为非对称结构，从而产生升力和侧向滚动力矩，以驱动弹头在飞行中产生螺旋机动。顾文锦等[5-7]系统性地将过载技术引入到了反舰导弹的机动变轨控制，具体实现方式是将反舰导弹的三维运动分解为纵向和侧向两个平面，让过载信号或视线角速度跟踪期望的正余弦信号。经过转化，反舰导弹可在三维空间运动并产生变轨轨迹。与顾文锦类似，韩国的RYOO等[8-9]也研究了反舰导弹对抗目标舰艇的作战场景。为定义滚转机动，文献[9]选择滚转轴作为导弹到目标的视线矢量，人为定义了滚转频率，弹体螺旋机动的加速度指令由速度矢量和螺旋角速度矢量叉乘得到。考虑到高度的限制，在开始螺旋机动时，滚转曲率半径最大，并随反舰导弹接近目标而单调减小，故选择适当的螺旋方向，可保证反舰导弹大于规定的高度，避免反舰导弹掉海。

在早期的研究中，导弹末端螺旋变轨机动飞行空域小，飞行马赫数不大，但其变轨控制技术对于研究高超武器的末端螺旋突防而言具有一定的借鉴和参考意义。宋贵宝等[10]针对反舰导弹面临的突防能力有限的问题，以视线角速率作为滑模面进行了改进。具体方法为，让视线角速率跟踪带有权重系数的正余弦函数，在高空时使权重保持常值，在低空时使权重系数变为0，这样可使得导弹在高空螺旋机动，在低空正常飞行。林鹏等[11]利用弹头内部的质量块移动，改变了弹头质心位置，实现了飞行器质心相对于气动力作用点的位置偏移，得到了质量块移动频率与弹道螺旋半径之间的关系。同样是变质心控制，王林林等[12]通过控制质量块的偏移，将速度和弹目连线的夹角控制在了固定值，并使得速度矢量可绕弹目视线旋转，实现了螺旋机动。何瑞智等[13]人为设置了惯性系下的纵向和侧向正弦轨迹形式，通过二阶导得到了过载指令，并将高度函数与最优指令进行了结合，通过仿真得到了三维螺旋俯冲轨迹，并且改变了正弦角速度倍数形式，可获得不同的轨迹形式。何磊等[14-16]引入了虚拟滑动目标，以对数螺旋运动模型为基础，利用曲线渐伸线原理设计了虚拟目标的滑动轨迹，采用了包含实变附加项的比例导引律追踪虚拟目标，引导高超滑翔器进行螺旋俯冲变轨。文献[16]基于凸优化理论，对飞行器动力学进行了重构，将非凸问题凸化后，进而离散，最后经迭代求解得到了最优螺旋轨迹的解。窦丛浩[17]采用与文献[10]类似的方法，基于一阶视线角相对方程，以纵向和侧向视线角为滑模面，设计了滑模制导律，并与螺旋信号进行了匹配，准确得到了螺旋轨迹。孔寒雪等[18]研究了稳定旋转导弹的锥形变轨运动，并揭示了锥形变轨运动的稳定性与弹旋速度的关系。LIANG等[19]考虑了导弹自动驾驶仪的动态特性，采用滑模变结构思路，让视线角速率跟踪给定的正弦信号，通过理论证明了制导律可收敛至滑模面，且跟踪误差趋于零。

从国外研究来看，除上述的RYOO等外，站在主动方角度设计变轨突防以提高高超飞行器生存概率的公开发表的文章并不多，并且大部分是站在了防御方的角度、想方设法研究性能更佳的制导律以对机动目标(“S”型、摆动型、螺旋型)进行拦截，重点在于对末端机动突防效果的定性研究上。PUAL等[20-21]采用简化的单时间常数制导系统方框图，通过伴随法，将阶跃机动、蛇形机动和螺旋机动分别对由比例制导的拦截弹产生的脱靶量进行了分析。分析结果表明，螺旋机动可增大脱靶量，更好地实现突防。DWIVEDI等[22]采用扩展卡尔曼滤波对螺旋目标信息进行了估计，结合预测制导，在测量的相对信息含有噪声或系统受限时，可以准确地用动能杀伤拦截机动目标。此外，FUMIAKI[23]和AKDAG[24]站在战斗机角度设计了螺旋机动和翻转机动两种方式，以对抗拦截导弹，仿真显示战斗机采用该机动模式可显著提高生存概率。

上述研究中的导弹飞行速度小、飞行空域低或站在防御方的角度研究问题等都不适合用于高超飞行器末端的主动突防研究。因此，本文以高超声速飞行器末端俯冲为研究场景，设计了一种变轨突防方案。通过将最优制导与螺旋机动相结合，控制飞行器在高空时进行主动螺旋变轨，以摆脱敌方拦截；在低空时进行精确制导，并以期望落角俯冲打击地面或海上高价值目标，在提高突防能力的同时也保证了命中精度。与相关参考文献相比，本文的创新主要体现在以下两个方面：

(1)与原文献中的比例螺旋相比，针对某些特定的打击任务(如实现天顶攻击，或要求从某种特定角度打击目标时)，文中将视线倾角λD作为系统的状态变量，并引入了终端落角约束，可实现上述攻击要求；

(2)针对变轨机动与精确制导两者相互依赖、互为矛盾的关系，本文通过设计正弦高度函数，实现了机动突防与精确制导的最佳匹配。与基于比例导引的螺旋相比，在相同的防空威胁下，本文设计的轨迹可成功完成突防任务，实现对目标的打击。

1 动力学模型阐述

1.1 坐标系定义

描述飞行器和目标在空中的位置关系，需建立弹道坐标系、视线坐标系、再入惯性坐标系。弹道坐标系为MXMYMZM，原点M取在飞行器的瞬时质心上，MXM轴与导弹速度矢量VM重合，MYM位于包含飞行器速度矢量VM的铅垂面并垂直于MXM，MZM轴垂直于其他两轴并构成右手坐标系；视线坐标系为MXLYLZL，原点M取在飞行器的瞬时质心上。MXL与飞行器和目标视线的连线重合，指向目标为正。MYL垂直于MXL指向上为正，MZL与两轴构成右手坐标系；再入惯性系为OXIYIZI，与地球固联。OXI指向正东，OYI指向天，OZI垂直于两坐标轴并构成右手坐标系。各个坐标系的转换关系如下

(1)

(2)

式中，it、jt、kt(其中t=M、L、I)分别表示三个坐标系坐标轴上的单位向量；λD、λT分别为视线倾角、视线偏角；θM、φM分别为飞行器相对于视线轴的相对倾角、相对偏角。坐标系的定义如图1所示。

图1 坐标系描述Fig.1 Description coordinate system

1.2 追逃运动矢量方程

根据图1的三维空中的飞行器与目标的几何关系，由矢量法则得到高超飞行器与目标的追逃方程[9]

AM=AxMiM+AyMjM+AzMkM=AxMiM+
ΩL×VM+ΩM×VM

(3)

式中，r为弹目位移矢量；AM为导弹在弹道坐标系内的矢量加速度；AxM、AyM、AzM分别为飞行器在弹道坐标系下各轴上的加速度分量；ΩL为飞行器与目标的视线角速度矢量；ΩM为飞行器相对于视线的角速度矢量。将式(3)转化为标量方程并进行坐标转换，可以得到飞行器相对倾角、相对偏角、速度的一阶动力学方程，以及飞行器与固定目标之间的相对运动方程

(4)

(5)

(6)

(7)

(8)

(9)

将飞行器在三维空中的运动分解为两个互相垂直的纵向和侧向平面。一般情况下，可认为飞行器与目标之间在纵向和侧向平面内的两个视线角速率趋于0，即认为满足制导精度，飞行器可以击中目标。在这里，将得到的式(8)和式(9)分别对时间进行求导，并将式(4)和式(5)代入整理，可得

(10)

2 基于最优控制的制导律设计

高超声速飞行器末段高马赫，在大空域俯冲飞行，受到的不确定扰动较多，会使得飞行器偏离目标。末段发动机已经关机，飞行器全部依靠空气动力完成飞行控制。为了使高超飞行器准确击中目标并具备更大的速度(动能)进行突防，选择终端脱靶量最小、能量消耗最小为性能指标，并进行最优控制设计。

2.1 相对运动方程的反馈线性化

式(10)具有强耦合项和非线性特点，不利于制导律设计，所以需引入反馈线性化[25]，令

(11)

式中，x1、x2为系统状态变量；u1、u2为系统控制输入；h1(x)、h2(x)为系统控制输出；λDF为纵向平面期望的落角约束；k>0，为常数。因此，可以将式(10)改写为非线性状态方程

(12)

式中

定义系统新的状态变量和控制变量为[25]

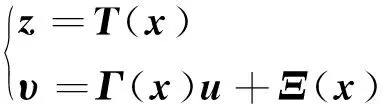
(13)

式中，z为新的状态变量；υ为新的控制输入；Γ(x)为转换矩阵。具体算式为

(14)

(15)

(16)

(17)

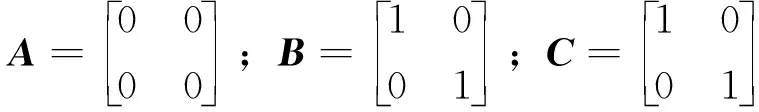
2.2 最优制导律设计

(18)

线性化后的系统最优控制输入为，υ=-R-1BTPz。其中，P可以通过逆的Riccati方程而得到：

(19)

(20)

令

tgo=tf-t

(21)

式中，tgo为任意时刻飞行器到达目标所需要的时间。逆时间积分式(20)，可得到

(22)

代入到P-1并且求逆，可得到

(23)

将得到的P代入υ，可得到线性化系统的最优控制输入为

υ=[-x1/tgo-x2/tgo]T

(24)

剩余时间的估计式为

(25)

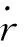
(26)

式(26)即为原非线性系统的最优控制输入。将文献[9]中的比例制导加速度信号作对比，可得

u=[AyMAzM]T

(27)

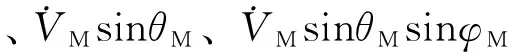
3 飞行器螺旋俯冲轨迹设计

3.1 螺旋信号设计

为使俯冲轨迹可以螺旋，可参考一般螺旋运动规律：物体在二维平面内进行圆周运动时，在物体上施加垂直二维平面的速度指令，则物体可在三维空间形成螺旋轨迹。同样，高超声速飞行器的螺旋可由一个螺旋主轴与螺旋频率来定义[9]

As=ωs×VM

(28)

式中，As为螺旋指令加速度矢量；ωs为螺旋角速度矢量，它可由弹头螺旋角速度与瞬时视线轴进行定义

ωs=ωsiL

(29)

式中，ωs是人为设定的螺旋角速度。螺旋指令的计算公式为

As=ωsiL×VM

=ωs(cosθMcosφMiM-sinθMcosφMjM+

sinφMkM)×VM

=ωsVMsinφMjM+ωsVMsinθMcosφMkM

(30)

螺旋信号的大小为

(31)

记cosθMcosφM=cosε[17]，则式(3)可变为

|As|=ωsVMsinε=ωsV1

(32)

式中，V1为飞行器速度VM在垂直于弹目视线方向上的分量；ε∈[0，π/2]。螺旋俯冲的原理图如图2所示。

图2 弹头产生螺旋的机动原理图Fig.2 Schematic diagram of spiral maneuver

飞行器在俯冲下降的过程中，其螺旋加速度|As|和飞行器速度分量V1始终在弹道坐标系平面MYMZM内产生平面的圆周运动，而飞行器则沿着视线的速度分量V2方向在进行平面圆周运动的同时沿着弹目视线方向前进，最后在三维空间合成螺旋运动轨迹。

3.2 最优制导与螺旋机动匹配设计

最优制导是指在满足最终期望状态与最小能量消耗的前提下，将飞行器准确地导引到目标位置。螺旋机动是在飞行器面临防空系统威胁的前提下做出的轨迹规避动作，用以突破敌方的防御，但其一定会降低制导精度。最优制导是目的，螺旋机动是前提，两者互相矛盾，但又彼此依赖，故两者如何实现匹配十分重要。设计的期望弹道坐标系的加速度为

(33)

τ(h)=sin[πh/2h*]

(34)

式中，Am为飞行器期望的加速度指令；h*为制导指令切换高度，gM为重力加速度在弹道坐标系下的投影；τ(h)为高度函数。为了防止期望的制导指令在高度切换时发生突变，可选用τ(h)使得两者可以平滑过渡。即总体思想为：先串行，后并行。

4 仿真验证

4.1 三维空中俯冲打击仿真

飞行器飞行过程中大气密度、总法向过载、动压、攻角、阻力系数的计算可参考文献[17]。飞行器初始下压点的坐标为[30000 30000 30000]m；目标位置为[0 0 0]m；初始相对倾角、相对偏角分别为θM0=6°，φM0=6°；初始速度为VM0=2400(m/s)；重力补偿为gI=[0, -g, 0]T；飞行器质量为600kg；参考气动面积为0.5m2；螺旋角速度为0.45rad/s；最优指令切换高度为12000m；纵向期望终端角为60°；比例制导系数N为3；k=1；弹道系过载范围限制为[-30g，30g]。其中，g=9.80665(m·s-2)，为重力加速度。

图3为三维空中两种螺旋轨迹的对比。由图3可以看到，两者都俯冲打击到地面固定目标点，但浅蓝色轨迹的螺旋半径要比红色轨迹的螺旋半径更大，这说明飞行器在空中螺旋飞行时的机动半径更大，飞行时间也相对更长。浅蓝色轨迹距地面一定高度进行了抬高，并以固定落角进入目标点。

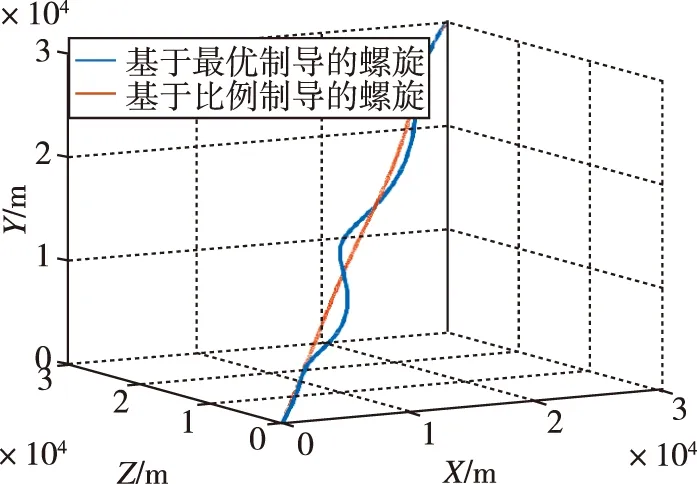
图3 飞行器三维空间飞行轨迹图Fig.3 3D flight trajectory diagram of vehicles

图4和图5分别为高超飞行器俯冲飞行时相对倾角θM、相对偏角φM随时间的变化示意图。

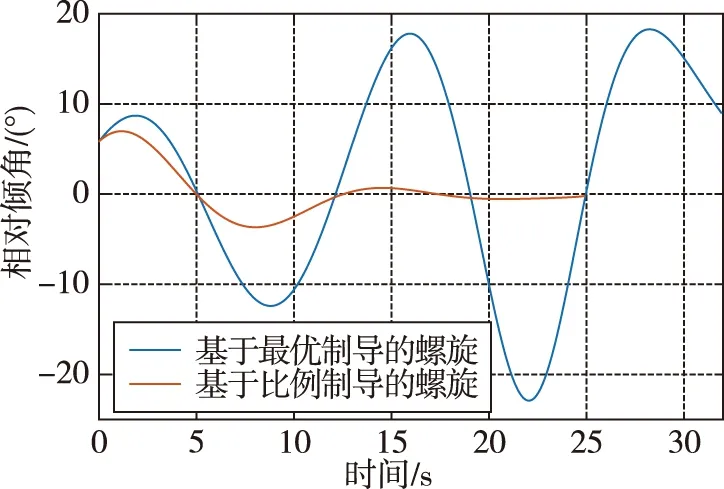
图4 飞行器相对倾角示意图Fig.4 The relative inclination of vehicle

图5 飞行器相对偏角示意图Fig.5 The relative deflection of vehicle

图6和图7分别为两种轨迹的过载变化过程。在弹道坐标系中，飞行器的纵向过载和侧向过载均为震荡形式，且都满足过载限制要求。由于最优制导的螺旋轨迹半径比后者半径要大，所以浅蓝色轨迹需要大的过载进行支撑，这也从图3中得到了验证。

图6 飞行器纵向过载示意图Fig.6 Longitudinal overload of vehicle

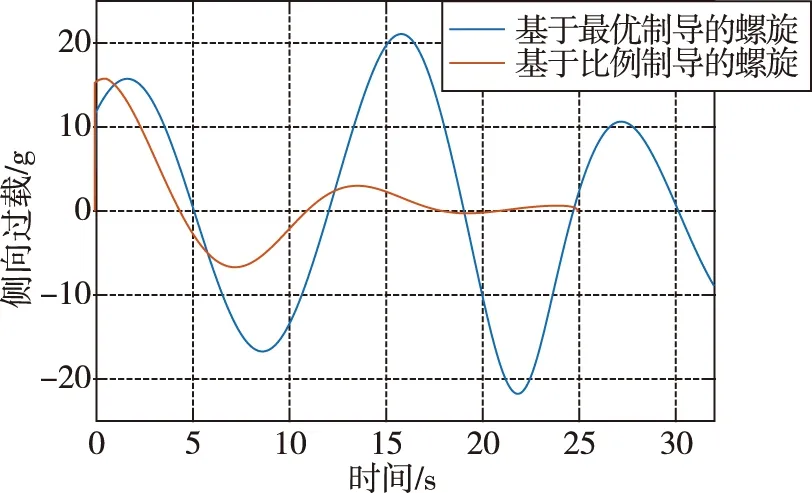
图7 飞行器侧向过载示意图Fig.7 Lateral overload of vehicle

4.2 突防评定

为了对两种轨迹的突防效果进行验证，参考文献[27]，拦截弹采用滑模制导律并分别对两种俯冲轨迹进行拦截。设在高超飞行器开始俯冲时，地面同时发射拦截弹进行空中拦截。拦截弹系数可参考文献[27]，速度始终为Ma=3，初始地面坐标点为[15000 20 15000]m。

4.2.1 基于比例制导的螺旋突防分析

由图8可知，基于比例制导的螺旋俯冲攻击在还没有打击到固定目标时(距离目标点2088.6m)，就已经被拦截弹所拦截，没有完成突防任务。由图9可知，拦截弹的侧向过载只在初始阶段产生了大的波动，随后逐渐平稳，并且始终位于要求的范围内。

图8 相对弹目距离变化示意图Fig.8 Schematic diagram of relative distance change

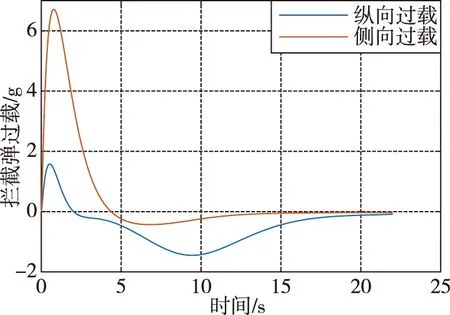
图9 拦截弹过载变化示意图Fig.9 Schematic diagram of interceptor missile overload

4.2.2 基于最优制导的螺旋突防分析

从图10来看，当飞行器打击到地面固定目标点时，拦截弹与飞行器的相对距离为12564.2m，这说明高超武器已完成任务，突防取得成功。在图11中，拦截弹的过载在28s前始终处于波动状态，这说明在高超武器大空域螺旋飞行时，拦截弹为了能够拦截高超武器，不得不也进行大范围的轨迹变化，但最终拦截失败。

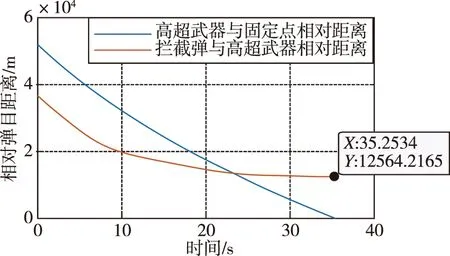
图10 相对弹目距离变化示意图Fig.10 Schematic diagram of relative distance change

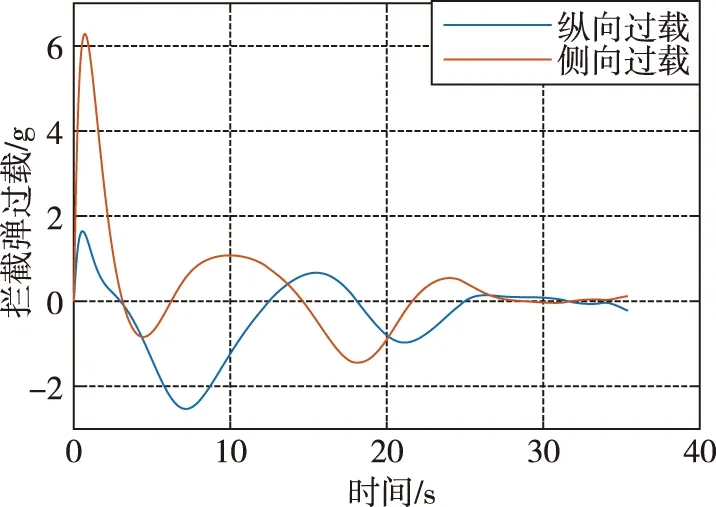
图11 拦截弹过载变化示意图Fig.11 Schematic diagram of interceptor missile overload

5 结 论

针对现实当中高超声速导弹末端打击敌方高价值目标为背景，本文重点研究了一种高超声速飞行器在俯冲段的突防办法。在面临愈加先进的敌方防御系统的背景下，本文将最优制导与螺旋机动进行了匹配结合。飞行器高空再入时，先进行大空域螺旋变轨，从而迫使敌方拦截弹因有限的机动能力而导致拦截失败；在进入低空后，飞行器逐渐转化为最优制导，并以期望冲击角打击地面目标，这样的方式同时兼顾了机动突防和精确制导两方面的优势。仿真实验表明，本文提出的方法可以增加高超飞行器的生存机会，而且可以成功完成突防任务，具有一定的实战应用前景。