预应力UHPC局部增强混凝土梁抗弯性能研究

2021-11-23曾勃曾国良

中外公路 2021年5期

曾勃，曾国良

(1.中国葛洲坝集团勘测设计有限公司，湖北武汉 430000；2.湖南联智科技股份有限公司)

超高性能混凝土(Ultra-High Performance Concrete，简称UHPC)是由水泥、硅灰、粉煤灰、高效减水剂、钢纤维以及石英细砂等组成的一种超高性能水泥基材料，具有强度高、韧性大、耐久性能优异等特点，可有望解决普通混凝土(Normal Concrete，简称NC)梁所面临的结构自重过大、跨越能力受限和耐久性不足等问题，在工程结构中具有广阔的应用前景。目前，国内外学者对全UHPC梁抗弯性能开展了大量的试验研究，结果表明：采用UHPC替代普通混凝土后能有效提高梁的抗弯承载能力，但受UHPC高昂造价的限制，其适用性并不强。为此，从提高性价比出发，不少学者开始对UHPC与普通混凝土组合梁的抗弯性能开展研究。徐世烺开展了超高韧性水泥基复合材料增强普通混凝土复合梁弯曲性能试验研究，给出了复合梁承载力理论计算公式；鞠彦忠探讨了UHPC-NC组合梁弯曲承载力的主要影响因素，指出界面粗糙度对承载力影响最大，UHPC厚度次之，UHPC水胶比影响最小；过民龙对UHPC-NC组合T梁静载抗弯性能开展了研究，分析了UHPC受拉区高度、NC强度等级、受拉纵筋率对组合梁抗弯承载力的影响；邓宗才从加固的角度出发，指出混杂纤维增强UHPC加固普通混凝土梁后其抗弯承载力显著提高。但上述研究中UHPC与普通混凝土组合梁受拉纵筋主要针对普通钢筋或高强钢筋，很少涉及预应力钢筋。考虑到UHPC-NC组合梁采用预应力钢筋后不仅能进一步提升其抗弯承载能力，增大结构的跨越能力，而且能降低UHPC的用量，取得良好的性价比。因此，对后张法预应力UHPC局部增强混凝土结构受弯性能开展研究具有非常重要的现实意义。

该文对后张法预应力UHPC局部增强混凝土梁开展抗弯承载力试验研究和理论分析。通过3根不同UHPC厚度预应力混凝土组合梁抗弯承载力试验，对试验梁的破坏特征、裂缝发展、承载特性及荷载-挠度曲线进行探讨，并基于试验结果对预应力UHPC局部增强混凝土梁承载力开展理论分析。

1 试验概况

1.1 试件设计

设计了3根预应力UHPC局部增强混凝土梁，梁长3.2 m，截面尺寸为300 mm×400 mm，其中UHPC层位于试验梁的底部受拉区，相应厚度t分别为0、50和100 mm。梁底纵筋采用直径16 mm的HRB400钢筋；梁顶架立筋采用直径10 mm的HRB400钢筋；箍筋采用直径为8 mm的HPB235钢筋，按构造布置；预应力筋为2根φj15.24的低松弛钢绞线，张拉控制应力为1 395 MPa，采用BM-3锚具进行锚固。试验梁截面配筋如图1所示，试件参数如表1所示，UHPC配合比如表2所示。

图1 试验梁配筋(单位:mm)

表1 试验梁参数 mm

表2 UHPC配合比

试验梁浇筑时，除试件U-0-PC一次成型外，其余两试件首先浇筑普通混凝土，然后在初凝前对界面进行压痕处理并喷洒TD-F2型液体界面剂，再浇筑UHPC层。试验梁浇筑完成1 d后脱模，并放置在室温下自然养护50 d后张拉预应力方可进行试验。试验梁制作时，预留同条件养护的立方体试块和棱柱体试块对UHPC以及普通混凝土基本力学性能进行测试。

1.2 材料性能

试验梁普通混凝土采用C40混凝土，相应的水泥∶水∶砂子∶石子质量配合比为415.4∶195∶605.82∶1 183.78。局部增强的UHPC配合比见表2，其中，水泥为42.5R普通硅酸盐水泥；粉煤灰等级为Ⅰ级，勃氏比表面为400～450 m2/kg；硅灰平均粒径为0.1～0.2 μm，勃氏比表面为20 000～25 000 m2/kg；石英砂粒径为40～80目；钢纤维长为12 mm，直径为0.2 mm，抗拉强度不低于2 800 MPa；聚丙烯纤维长6 mm，直径为0.02 mm，抗拉强度不低于600 MPa；减水剂为萘系高效减水剂，减水率大于30%；减缩剂为SBT-SRAI类型。在常温养护50 d后实测C40混凝土和UHPC标准试块的力学性能如表3所示，其中ft为劈裂抗拉强度，fc为棱柱体抗压强度，fcu为立方体抗压强度，Ec为弹性模量。普通钢筋与预应力筋的实测力学性能见表4。

表3 混凝土力学性能

表4 钢筋实测力学性能

1.3 加载方案及测试内容

试验梁采用三分点分级加载，其中纯弯段长1 000 mm，如图2所示。试件加载前，需进行预压；试件正式加载后，每级加载均持荷5 min，待荷载与跨中挠度均稳定后再采集数据。具体步骤如下：

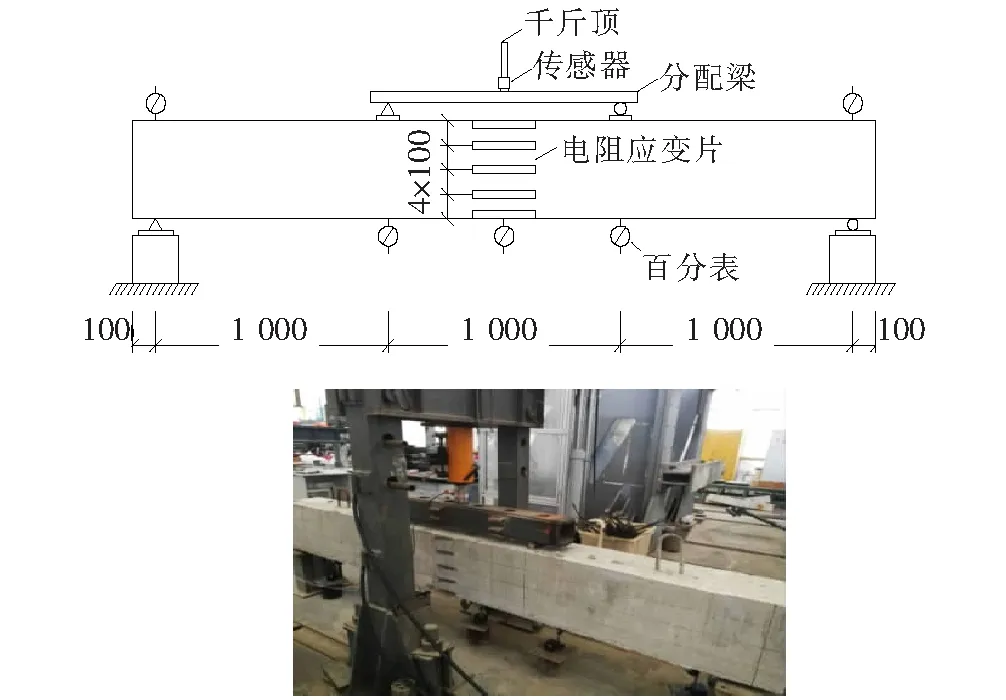
图2 试验梁加载示意图(单位:mm)

(1)首先对试件进行预压，预压荷载为15 kN，持荷5 min，调试仪器并卸载，待试件卸载变形稳定后，对力传感器及电阻应变片读数调零，并对纯弯段百分表初读。

(2)对试件开始加载，试件开裂前以每级10 kN加载至近开裂荷载，然后以5 kN为一级加载至试件开裂。

(3)试件开裂后，以15 kN为一级加载，持荷5min，当荷载稳定后，详细记录裂缝的长度、宽度与新裂缝的生成情况。

(4)当纵筋屈服后，按跨中挠度变形对试件进行加载，挠度控制变形值每级5 mm；当上缘混凝土压碎时认为其达到破坏，随后开始卸载。

试验测量内容包括：竖向荷载、跨中挠度、跨中沿截面高度混凝土应变、纵筋和钢绞线应变、裂缝分布及宽度。其中，竖向荷载通过量程1 000 kN的千斤顶施加；跨中纯弯段挠度采用百分表测量，百分表在纯弯段纵向布置3组，间距500 mm；试验梁裂缝使用放大镜和KON-FK裂缝宽度检测仪进行详细观察和测量。为观察预应力UHPC局部增强混凝土梁截面是否符合平截面假定，在梁跨中侧面沿梁高方向粘贴5片电阻应变片，间距100 mm；纯弯段纵筋、钢绞线表面布置应变片，并测量其应变，相应的应变采用静态应变测试仪采集。

2 试验结果与分析

2.1 破坏过程及破坏形态

3个试件均表现出适筋梁破坏特征，最终裂缝开展情况如图3所示。

图3 试验梁破坏时裂缝分布

试件破坏过程如下：

试件U-0-PC在荷载为45.9 kN时，纯弯段梁底出现第一条微观裂缝；继续加载，在弯剪段开始出现斜裂缝，裂缝宽度和数量随荷载的增大而增加，当荷载达到109.5 kN时，梁底纵筋开始屈服，此时纯弯段新裂缝基本不出现，原有裂缝宽度扩展并向上延伸，并在纯弯段中心靠左位置形成一条主裂缝；当荷载达到130.1 kN时，上缘混凝土被压碎，试验梁产生破坏，此时主裂缝宽度接近2 mm。试件破坏时纯弯段裂缝数量较少，宽度明显大于其他两试件，如图3(a)所示。

试件U-50-PC在加载到51.9 kN时，在跨中纯弯段开始出现竖向裂缝；当加载至123.7 kN时，试件底缘纵筋开始屈服；继续加载至148.4 kN时，上缘混凝土压碎形成贯通的横向裂缝导致试件破坏。与试件U-0-PC相比，由于梁底UHPC的控裂作用，裂缝扩展速率明显放缓，梁最终破坏时，主裂缝宽度变小，约为1.3 mm，表明UHPC局部增强对裂缝发展起到较好的抑制作用，使原本宽而少的裂缝转变为细而密的微细裂缝，如图3(b)所示。

试件U-100-PC裂缝开展和荷载变化与试件U-50-PC相似，由于UHPC局部增强层厚度的增加，相应的开裂荷载、屈服荷载和极限荷载分别增大到73.1、149.8和175.4 kN，虽然开裂荷载增长幅度不大，但屈服荷载和极限荷载增加明显，表明增大UHPC层厚度能显著提高梁的承载特性。与试件U-50-PC相比，试件U-100-PC破坏时最大主裂缝宽度进一步减少至1 mm左右，且在纯弯段裂缝分布更密，在弯剪段裂缝有向支点扩展的趋势，部分裂缝甚至出现在UHPC与普通混凝土界面位置，但并未扩展至梁底，如图3(c)所示。

2.2 荷载-挠度关系

图4为试验梁实测的跨中荷载-挠度曲线。从图4可以看出：① 3组试件分别经历了弹性工作阶段、带裂缝工作阶段和屈服、破坏阶段；② 加载初期，3根试验梁为弹性阶段，荷载-挠度曲线为线性关系，但初始刚度随UHPC层厚度的增加而增大；③ 截面弯矩达到初裂弯矩后，试件逐渐进入弹塑性受力阶段，曲线斜率开始变缓，由于UHPC中钢纤维的阻裂作用，局部增强后试件的初始开裂应变大于普通混凝土试件；考虑到钢纤维的桥联作用抑制裂缝的扩展，UHPC局部增强梁的弯曲裂缝以多裂缝模式扩展(普通混凝土裂缝少，宽度大)，即当UHPC基体达到开裂应变后又出现新裂缝，进而在UHPC增强层形成许多细而小的裂缝；④ 纵筋屈服后，试件进入屈服破坏阶段，此时受拉区普通混凝土退出工作，导致截面抗弯刚度下降，荷载-挠度曲线出现了转折；试件在到达极限荷载后，梁顶受压边缘被压碎、预应力筋发生屈服，荷载-挠度曲线出现下降，试验梁迅速丧失承载力。考虑到UHPC中钢纤维的阻裂作用，试验梁极限弯矩随UHPC层厚度的增大而显著增加，当UHPC层分别由0 mm增加到50 mm和100 mm时，极限弯矩分别提高约1.14倍和1.35倍。

图4 试验梁跨中荷载—挠度曲线

2.3 跨中截面应变变化

3根试验梁的跨中截面应变分布如图5所示。

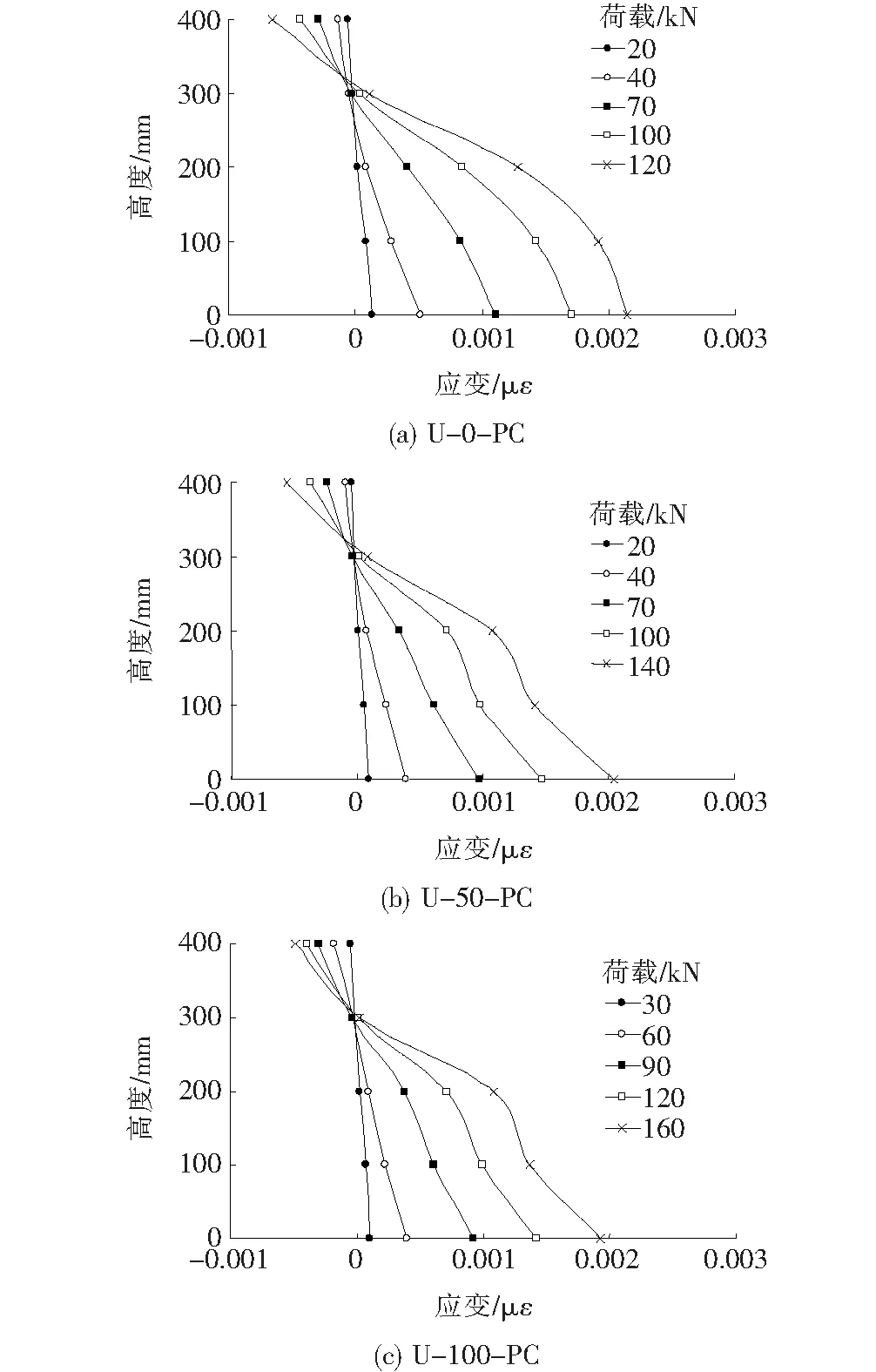
图5 试验梁跨中截面应变

从图5可以看出：3根试验梁跨中截面弯曲正应变沿梁高方向的分布基本符合平截面假定，在开裂前，中和轴基本保持不变，开裂后，截面受拉区应变越来越大，中性轴高度逐步上升，截面受压区高度随之变小，受压区混凝土应变逐渐增大，两根UHPC局部增强预应力混凝土梁的最终破坏形态与预应力混凝土梁相同，表明组合梁截面协同工作性能较好。

3 开裂弯矩和极限弯矩计算

3.1 基本假定

(1)截面符合平截面假定，应变沿梁高线性分布。

(2)主梁开裂后，受拉区普通混凝土失效，UHPC继续工作直至试件破坏。

(3)试件破坏以受压普通混凝土被压碎为准则，此时预应力筋和非预应力筋均已进入屈服。

(4)混凝土与预应力筋、非预应力筋之间无滑移。

3.2 材料本构关系

3.2.1 普通混凝土本构关系

普通混凝土本构关系采用GB 50010—2010《混凝土结构设计规范》推荐的简化模型，其中受压应力-应变关系为：

(1)

式中：σc和εc分别为混凝土压应力和压应变；fc为混凝土轴心抗压强度；ε0为混凝土峰值压应变，按0.002取值；εcu为混凝土极限压应变，按0.003 3取值。

3.2.2UHPC受拉本构关系

UHPC受拉应力-应变曲线采用简化模型，其表达式为：

(2)

式中：σt和εt分别为UHPC拉应力和拉应变；Eu为UHPC抗拉弹性模量，取44 700 MPa；ftr,u为UHPC的抗拉强度，取6 MPa；εtr,u为UHPC的开裂拉应变；εtu,u为UHPC的极限拉应变，取0.007。

3.3 开裂弯矩

根据JTG D62—2012《公路钢筋混凝土及预应力混凝土桥涵设计规范》规定，预应力受弯构件开裂弯矩可用以下公式计算：

Mcr=(σpc+γftk)W0

(3)

(4)

式中：σpc为扣除全部预应力损失后预应力筋在梁底边缘产生的混凝土预压应力；γ为受拉区混凝土塑性影响系数；ftk为混凝土抗拉强度标准值；W0为换算截面抗裂边缘的弹性抵抗矩；S0为全截面换算截面重心轴以上(或以下)部分面积对重心轴的面积矩。

UHPC由于钢纤维的桥联作用，对抑制裂缝的生成与发展具有显著的作用，其抗拉强度远高于普通混凝土，并能有效提高受拉区混凝土塑性变形高度。为此，引入增强系数α考虑UHPC中钢纤维的阻裂作用，综合式(3)，建立预应力UHPC局部增强混凝土梁开裂弯矩表达式为：

(5)

(6)

式中：λ为钢纤维抗裂影响系数，根据文献[6]取λ为0.2；ρ为钢纤维体积率；l和d分别为钢纤维长度和直径；t和h分别为UHPC厚度和主梁截面高度；ftr,u为UHPC抗拉强度。

3.4 极限弯矩

预应力UHPC局部增强混凝土梁到达承载极限状态时，受压区普通混凝土达到极限压应变，梁开始发生破坏，此时主梁受拉区预应力筋和非预应力筋均已达到屈服，相应的截面应力应变分布如图6所示。其中xc为受压区高度；εp和εs分别为受压区顶缘普通混凝土达到极限压应变εcu时受拉区预应力筋和非预应力筋对应的应变；β为受压区等效矩形应力图高度系数，按0.8取值；fpy和fsy分别为预应力筋和非预应力筋的屈服强度，按表4取值；受拉区UHPC按基本假设以等效矩形考虑，高度为t，应力取UHPC抗拉强度ftr,u。