2K-V型减速器柔体动力学模型验证分析

麻东升，谭 鹏

(1.天津工业职业学院机械工程系，天津 300400；2.天津职业技术师范大学机械工程学院，天津 300222；3.天津市高速切削与精密加工重点实验室，天津 300222；4.潍坊职业学院机电工程系，山东 261000)

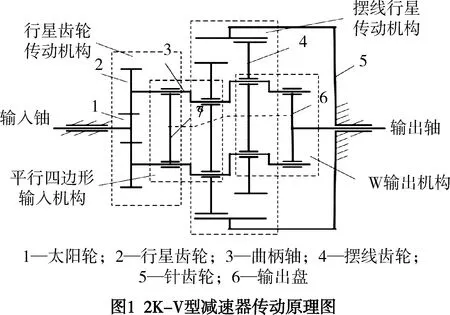
2K-V型传动是一种双曲柄式少齿差行星齿轮传动[1]。这种传动利用平行四杆机构与齿轮机构的组合，变成双曲柄式行星传动机构，其传动原理图如图1所示。由于内啮合的摆线齿轮4、针轮5的齿数相差为1，所以可归类为少齿差类行星传动[2]。其广泛应用于航空航天、汽车制造等传动装置方面[3]。

随着计算机技术的发展，越来越多的产品进行分析与计算，降低产品的生产周期与成本，其中虚拟样机技术已成为关键点，为虚拟建模环节提供了可视化操作，但是虚拟建模中的一些核心问题需要我们亟待解决[4]。

本文以ADAMS软件为平台，对2K-V40型减速器进行动力学仿真研究，创建了动力学刚柔耦合模型，通过对模型转速进行分析后，验证了模型的正确性。此外，利用ADAMS/Flex模块和ADAMS/AutoFlex模块对第二级针齿与摆线轮进行动强度和应力分布分析[5]。

1 针齿柔性体系统模型

利用ANSYS软件建立针齿柔性体模型，在定义了“拉伸路径”、“单元尺寸和“外部节点”之后生成的针齿柔性体模型如图2所示。

通过在ADAMS/Flex模块中选前20阶模态，定义了两个外部节点，故在ADAMS/Flex模块中可看到如表1所示的32阶固有频率数据。

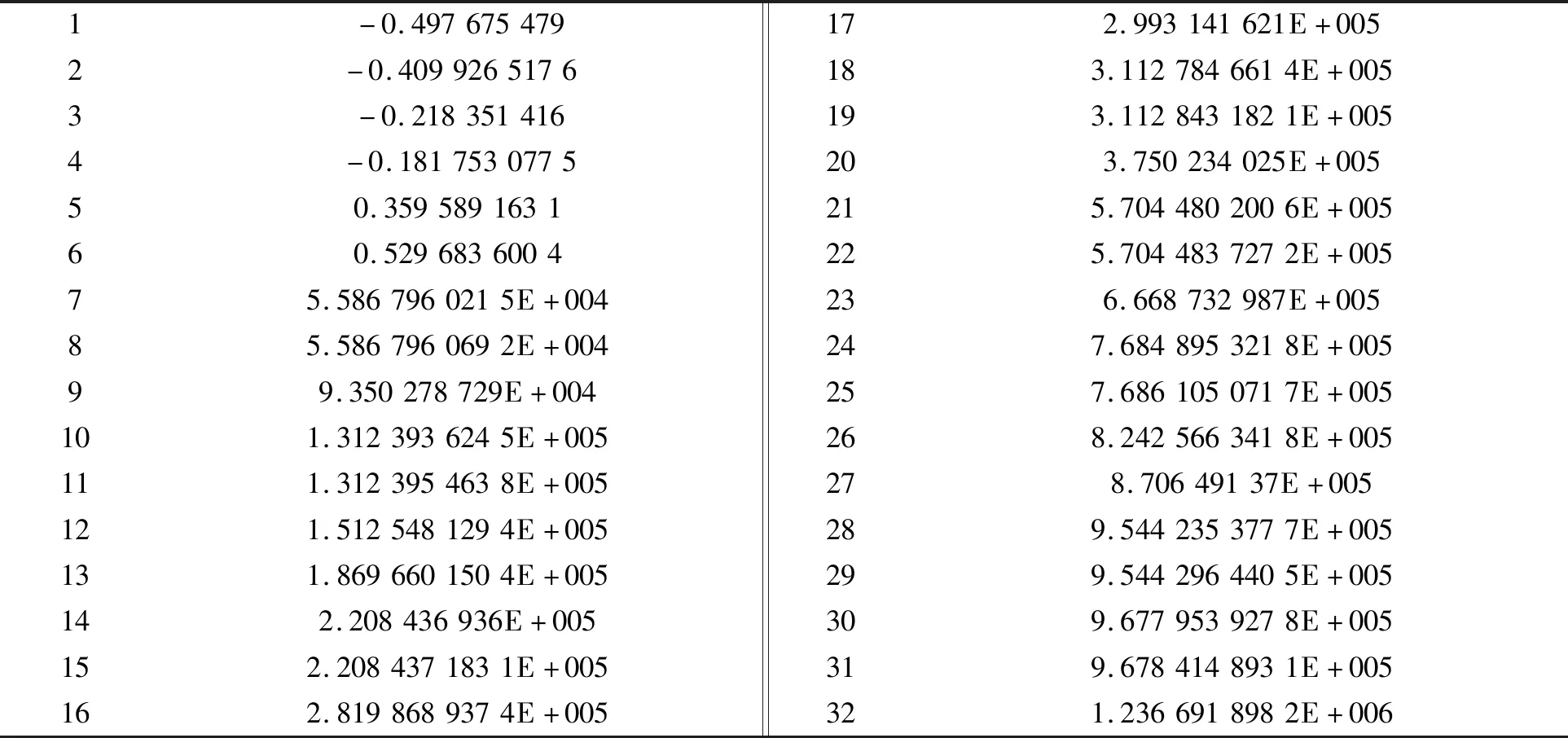
表1 针齿模型正交化固有频率

对于针轮，每一个齿的承载状况是相同的[6]，因此只需建立单个针齿的柔性体模型。在仿模型中由于质量为零，而零件的自由度不为零。在求解过程中会导致出现奇异矩阵[7]，所以不能将所选刚性针齿的密度设置为零。由于针齿刚性体的质量几乎为无限小，不会影响系统的动力学特性，生成的针齿柔性体系统模型如图3所示。

对该模型进行转速验证：其仿真结果如图4、5、6所示。多刚体动力学仿真的设置如下[8]：

(1)关闭“执行图形显示”可以加快仿真速度；

(2)由于系统自由度增多，仅针齿柔性体就有50个自由度，所以不使用阶跃函数定义驱动。

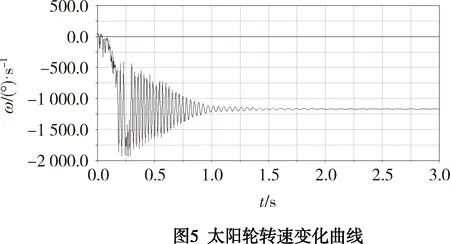
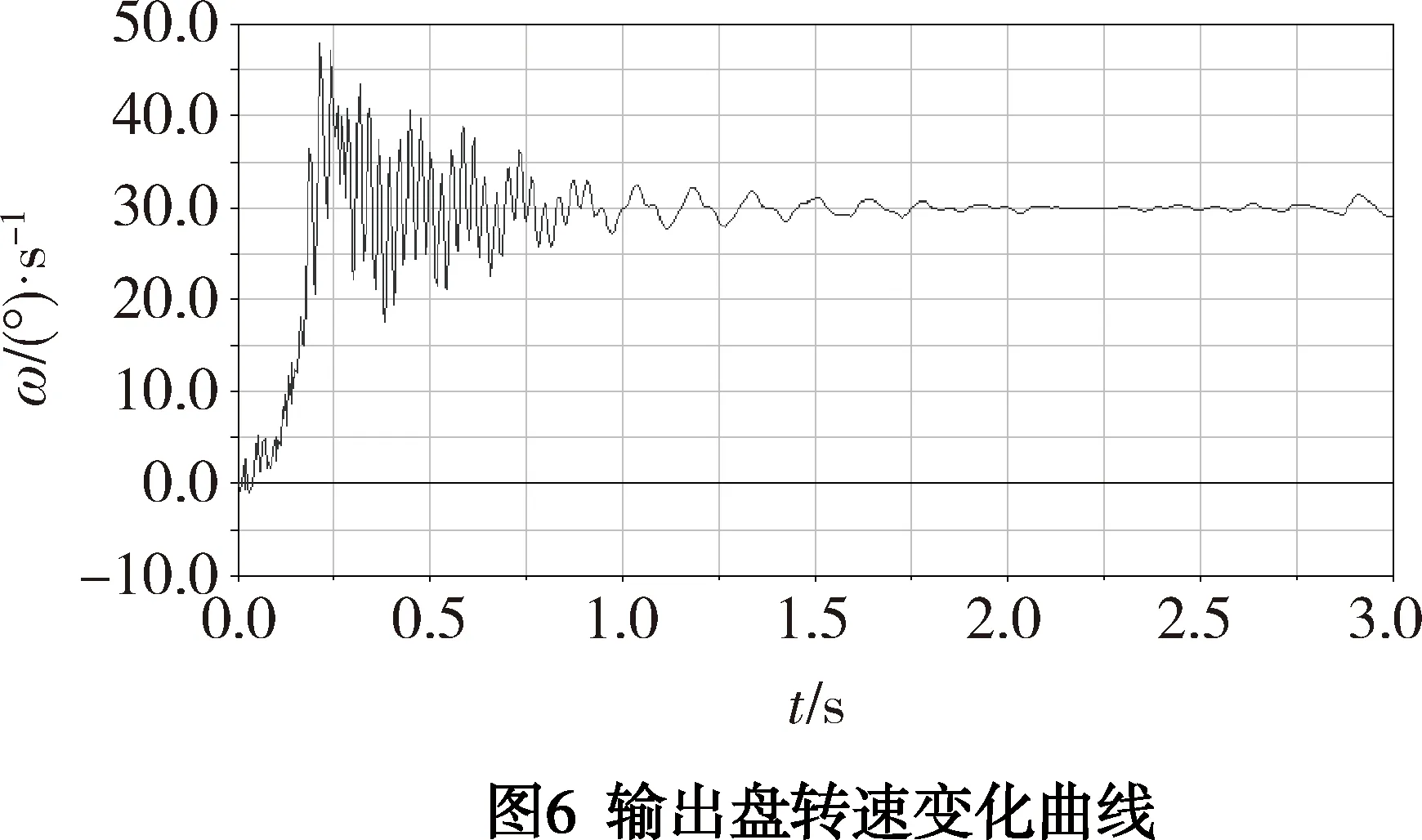
根据图4、图5和图6中曲线，可以作如下分析:

(1)从转速方向上分析

由于图4和图6转速数值为正，则表示输入轴和输出盘转速方向为逆时针；图5转速数值取负，表示太阳轮转速方向为顺时针。

(2)从转速大小上分析

当输入轴转速恒定时，太阳轮、输出盘转速从0到1 s波动较大，1 s之后它们的转速平稳运行；由于齿轮传动过程中存在不可避免的振动和冲击，太阳轮和输出盘转速会出现微小的速度波动。各零件转速的数据值如表2所示。

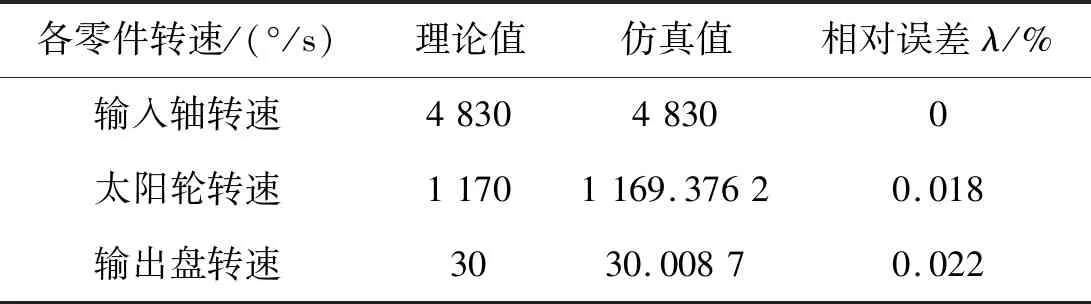
表2 各零件转速数据值

由表3数据可以得知：柔性体系统模型的各级转速的相对误差λ有增大，因此为保证2K-V型减速机较高的精度，针齿应采用硬度较高的材料。

2 针齿的动强度分析

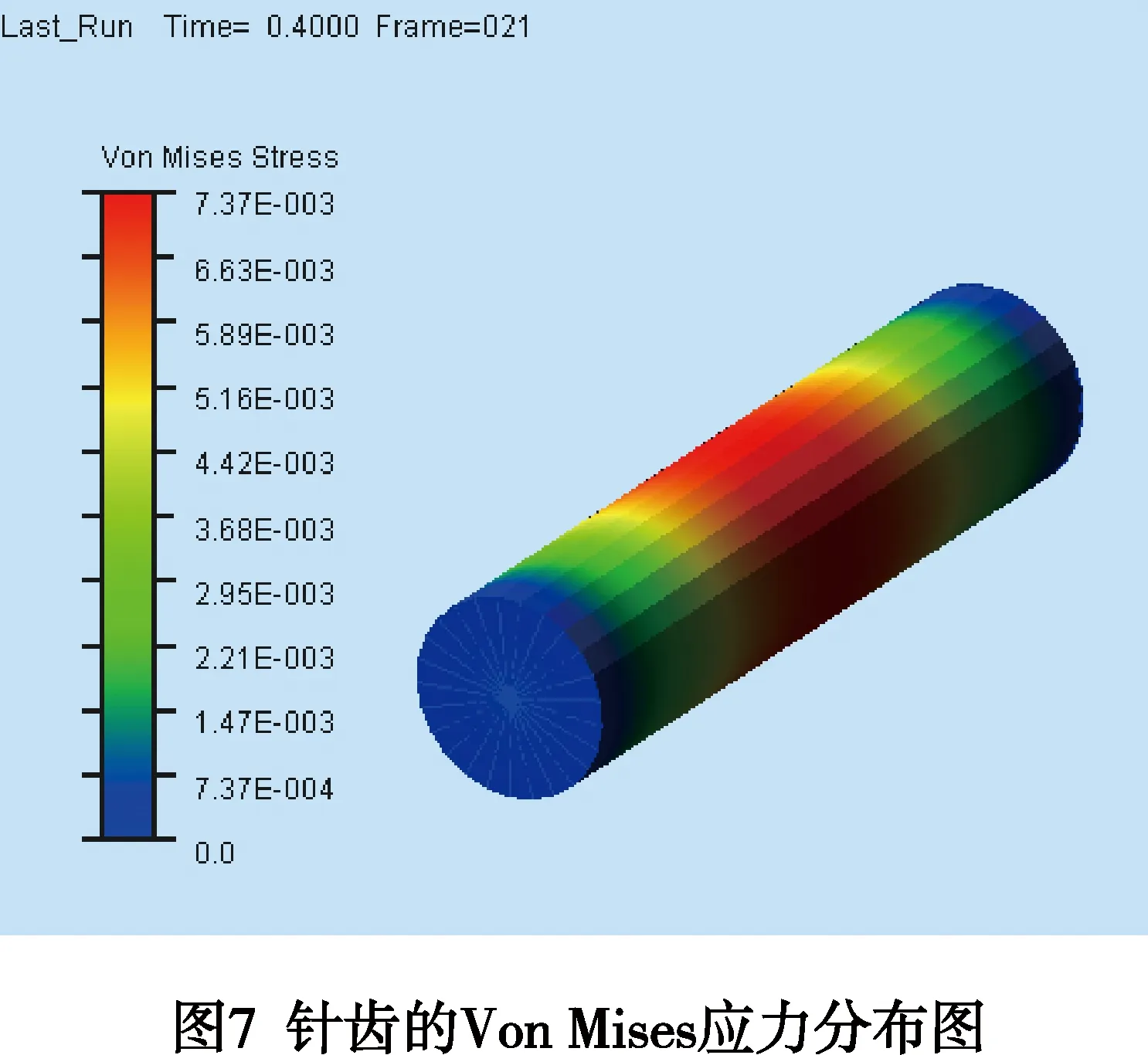
利用ADAMS软件得到针齿的Von Mises应力变化的情况，如图7所示。由图7可以得知针齿的Von Mises应力分布情况：针齿的中部应力最大，根据左侧的应力彩色标尺，应力最大值可达到7.37E-003 N/mm2；应力值由针齿中部向两端逐渐减小，并且呈对称分布。在ADAMS/PostProcessor的界面上出现 “热点”标签，通过该标签可以定位和观察热点信息，如图7所示。其中，节点429、430和432处出现的Von Mises应力最大，并且这些节点都集中在针齿的中部，即针齿质心位置处，如图8所示。

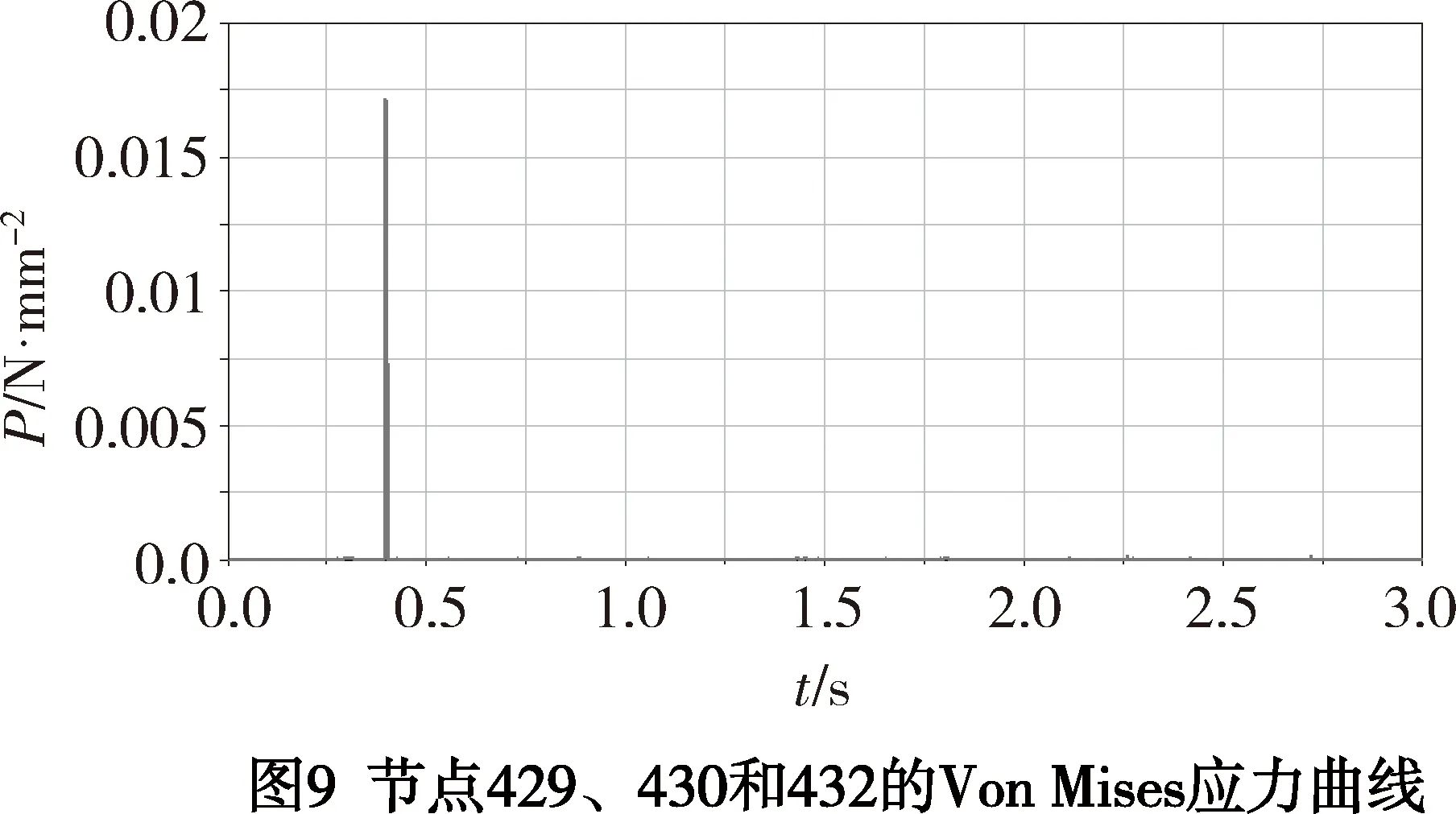
针齿节点的Von Mises应力的变化曲线如图9所示。

根据图9的数据可知：节点429、430和432的Von Mises应力随时间的变化情况相同，均是在转速平稳之前的0.399 1 s出现应力的第一个峰值0.017 22 N/mm2，在0.4 s出现应力的第二个峰值7.37E-003 N/mm2，其中0.4 s时针齿的Von Mises应力分布情况如图7所示。在0.5 s之后，Von Mises应力很小，均值为4.300 9E-006 N/mm2，最大值也只有1.765E-004 N/mm2。

3 针摆柔性体系统模型

通过ADAMS/Flex模块生成摆线轮的模态文件，由于在ANSYS中提取了前20阶模态，定义了两个外部节点，故在ADAMS/Flex模块中可看到如表3所示的32阶固有频率数据。

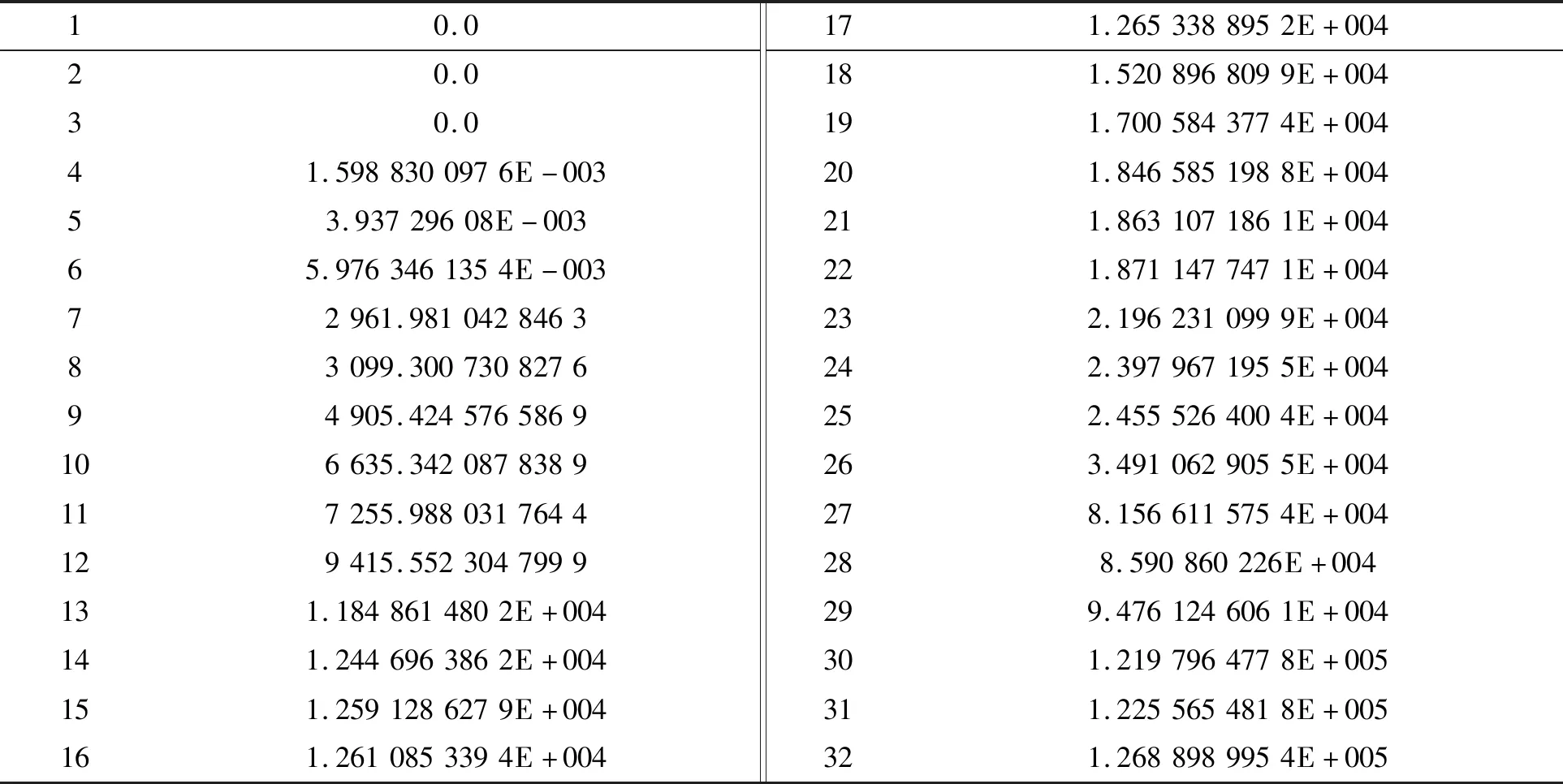
表3 摆线轮模型正交化固有频率

建立刚柔耦合模型，如图10所示。运用固定约束在外部节点处将摆线轮柔性体分别与两个虚构件连接起来，生成的针摆柔性体模型如图11所示。

对针摆柔性体模型进行动力学分析，结果如图12、13、14所示。

利用ADAMS/Postprocessor的后理功能按2 s到4 s转速平稳阶段各零件转速的平均值选取，如表4所示。

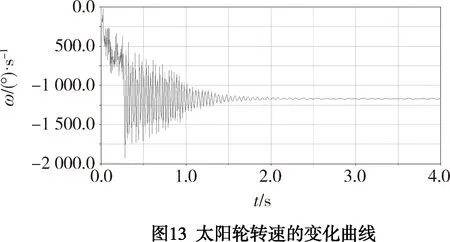
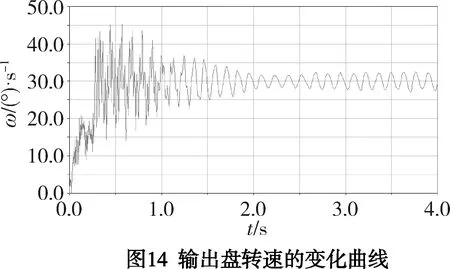
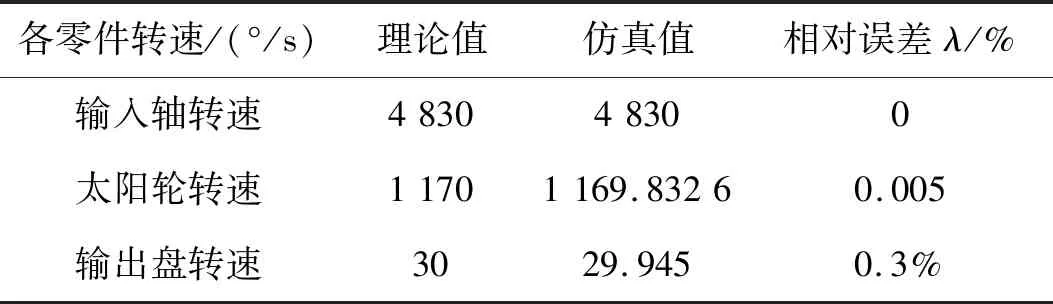
表4 各零件转速数据值

综上所述，针摆柔性体模型的输出盘转速的相对误差λ比多刚体系统模型大一个数量级，所以摆线轮的硬度对2K-V型减速器的传动精度影响较大。

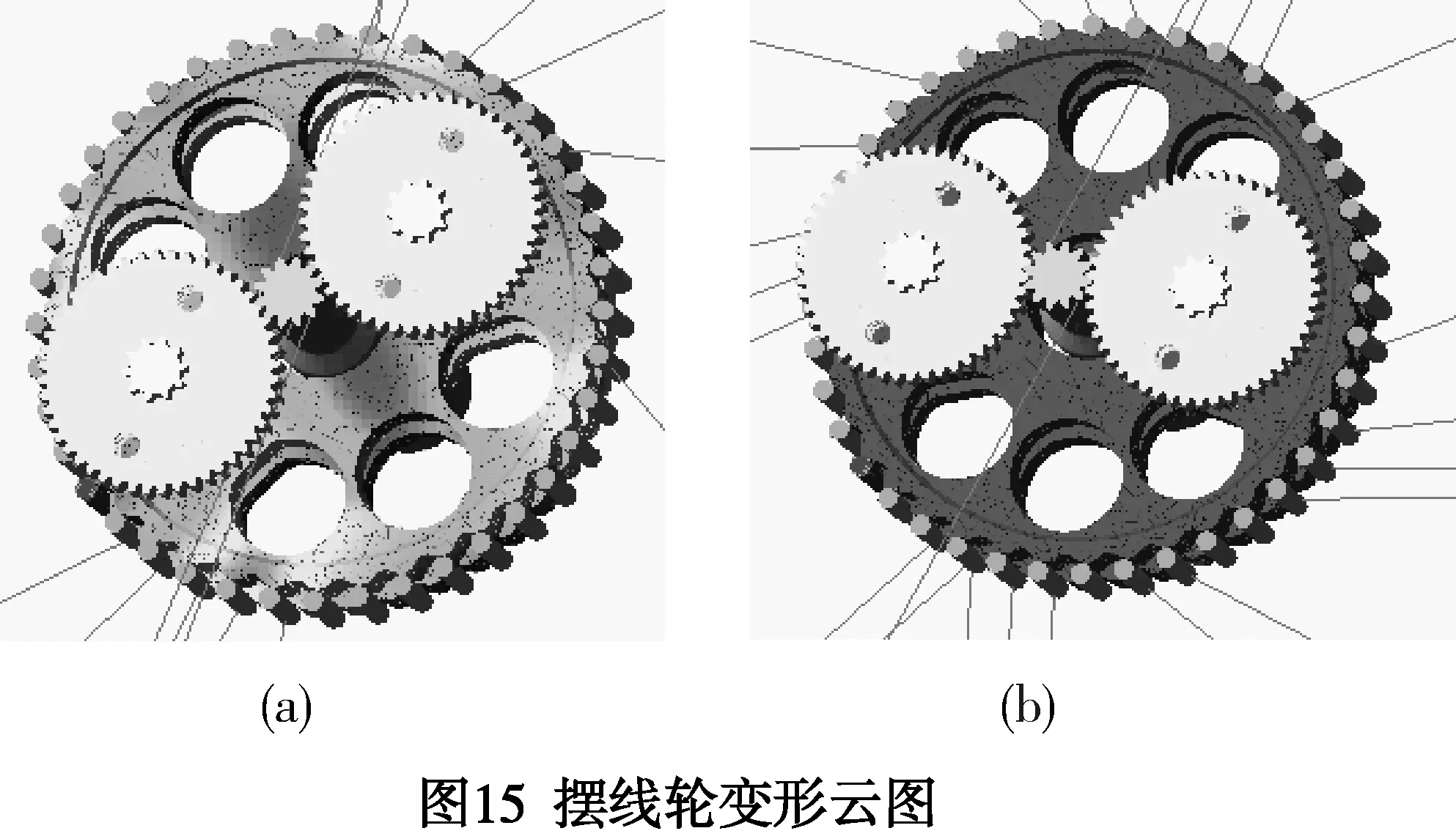
观察针摆柔性体系统模型的仿真动画，可知摆线轮的变形情况，某时刻摆线轮变形云图如图15所示。在转速平稳之前(即2 s之前)，摆线轮的变形较显著，尤其是齿圈部位变形较大，如图15(a)所示；在2 s之后，摆线轮处于转速平稳阶段，变形也不再那末剧烈，如图15(b)所示。因此，在摆线轮制造过程中，应注意采取必要的工艺措施提高摆线轮齿圈硬度，从而提高传动精度和传动效率。

4 摆线轮的动强度分析

与针齿动强度的分析方法相同，综合运用ADAMS/Durability模块和ADAMS/PostProcessor模块，摆线轮的Von Mises应力云图如图16所示。由图16可以得知某时刻摆线轮的Von Mises应力分布情况：两个扇形孔与其之间的圆孔交界处应力值最大，根据左侧的应力彩色标尺，应力最大值可达到1.68E-002 N/mm2，远远大于针齿的应力最大值。另外，在整个仿真动画显示过程中，除了开始时刻(转速平稳前)应力分布不均匀外，摆线轮的应力分布变化不明显，如图17所示。其中，摆线轮Von Mises应力最大值出现在节点520处，应力值最大的节点出现在5 428处。

节点的Von Mises应力的变化曲线如图18、19所示。

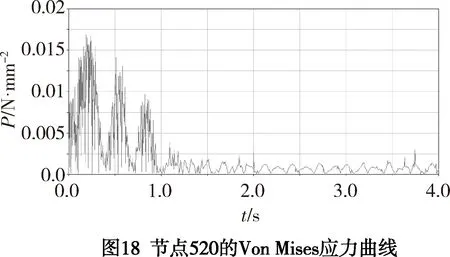
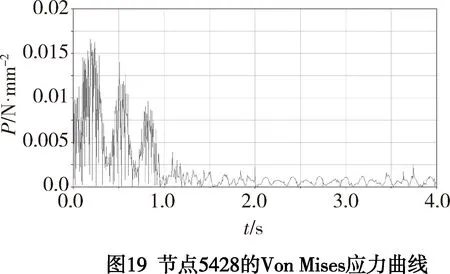
根据图18和图19的数据可知：节点520和5428的Von Mises应力值在转速平稳之前(即2 s之前)波动很大，并且节点520的应力最大值为1.68E-002 N/mm2，节点5 428的应力最大值为1.65E-002 N/mm2；在2 s之后，Von Mises应力呈周期性正弦规律变化，均值分别为6.789 4E-004 N/mm2和5.929 2E-004 N/mm2。

摆线轮的Von Mises Strain应变云图如图20所示。与Von Mises应力随时间变化的情况相同：除了开始时刻(转速平稳之前)应变分布不均匀外，摆线轮的应变分布没有明显的相对变化，应变值很小。应变主要集中在两扇形孔与其之间的圆孔交界处和曲柄轴承孔附近。

普通轴承钢如果热轧不退火的话，其强度指标通常不做考量，一般为950～1 100 MPa，远远大于上述Von Mises应力仿真结果；热处理后能达到HRC60的硬度，强度也超过1 800 MPa。因此，可以只对摆线轮的齿圈部位进行热处理，从而达到降低加工成本的目的。

5 结论

(1)利用ADAMS/Flex模块创建针摆刚柔耦合系统模型，并验证模型的正确性，得到摆线轮系统变形的情况；综合运用ADAMS/Durability 模块和ADAMS/PostProcessor模块对摆线轮的动强度进行分析，得到摆线轮的Von Mises应力和Von Mises Strain应变分布数据；

(2)根据针齿和摆线轮的应力分析结果，摆线轮的应力最大值远远大于针齿的应力最大值，因此应注意提高摆线轮的强度，避免摆线轮的强度薄弱位置(即两扇形孔与其之间的圆孔交界处)超过许用应力，为摆线轮的优化设计提供了理论依据；

(3)根据针摆模型仿真结果的相对误差λ，采取必要的加工工艺措施提高摆线轮齿圈硬度，是通过提高第二级行星传动的精度来提高2K-V型减速机传动精度和传动效率的有效途径。