最大相关峭度解卷积的改进及在往复压缩机气阀故障诊断中的应用
2021-11-23王金东李云峰赵海洋李彦阳
王金东,李云峰,赵海洋,李彦阳
(东北石油大学机械科学与工程学院,黑龙江 大庆 163318)
气阀作为往复压缩机重要的功能性组件,长期处在交变冲击载荷作用下,其内部构件极易发生故障【1】。阀盖测点采集的振动信号呈高度非线性、非平稳性的特点,且往往表现为较强烈的噪声突变和振幅畸变,基于传统的振动信号分析故障诊断方法很难准确地提取故障特征【2】。
最小熵解卷积(Minimum Entropy Deconvolution,缩写为MED)由Wiggins等提出。MED方法通过设计一个逆滤波器使信号的峭度达到最大化,从而消除信号中的噪声。H.Endo等首次将其用于齿轮的故障诊断。MED方法的优点是能解卷积出单个脉冲特征【3】,但故障的冲击成分具有周期性,为弥补MED方法的不足,McDonald等人【4】利用故障的周期性,通过迭代选择最佳滤波系数,使滤波信号的相关峭度达到最大化,这种新的方法称为最大相关峭度解卷积(MCKD)。MCKD方法的精确性在很大程度上取决于初始对故障周期的准确估计,而且当遇到波动周期时,其效果就会受到严重影响【5】。张晓涛等【6】提出一种改进MCKD的降噪方法。该方法采用双向循环重构的滤波准则,具有较好的降噪效果,但也需要预估准确的故障周期。针对MCKD方法的局限性,本文对其进行了改进。新方法将自相关函数和双向重构准则的相关峭度【7】相组合,应用于往复压缩机故障诊断,可实现故障特征的准确提取。
熵值分析能检测复杂信号稳定性,是非线性时间序列分析的一种新方法,在机械设备故障诊断领域得到了广泛的应用【8】。模糊熵(Fuzzy Entropy,缩写为FE)作为样本熵的改进,是单一尺度上度量时间序列复杂性的一种新方法【9】,它定义的阈值划分更为合理,具有较好的量化效果。机械系统具有复杂性,振动信号中与故障有关的信息常包含在多个尺度上,致使模糊熵、样本熵无法准确度量时间序列复杂度。Costa等人提出了多尺度熵(Multiscale Entropy,缩写为MSE),为细致描述非线性时间序列复杂度提供了一种新途径。但MSE在度量相似性时会发生突变,而且对时间序列的长度依赖性较大。为此郑近德【10】借鉴多尺度熵思想提出了多尺度模糊熵(Multiscale Fuzzy Entropy,缩写为MFE),该方法用各个不同时间尺度刻画故障信息复杂程度,但是利用MFE计算粗粒化序列会导致熵值不够全面、准确【11】。经过比较,精细复合多尺度模糊熵(RCMFE)相比于其他多尺度熵具有更高的熵值估计准确性,以及较低的未定义熵概率。因而本文将RCMFE引入到往复压缩机气阀故障振动信号的多尺度复杂性分析中,进而提出一种全新故障特征分析方法。
鉴于往复压缩机的气阀受强烈气体波动干扰的工况特性,本文针对气阀振动信号进行分析,提出一种基于改进MCKD与RCMFE相结合的往复压缩机气阀故障诊断方法。该方法对所采集信号进行解卷积,从而突出信号中冲击成分,能有效提取气阀故障特征分量,具有更快的计算时间和更高的故障识别率,提高了故障诊断的精确度。
1 改进的最大相关峭度解卷积算法
1.1 最大相关峭度解卷积
最大相关峭度解卷积算法的本质是通过最大化相关峭度来获得最佳滤波器,将冲击信号y从原始信号x中恢复出来,达到抑制噪声、突出故障冲击分量的目的,即
(1)
其中
式中:x——输入信号;
f——滤波器系数,f=[f1,f2,f3…fL]T;
L——滤波器长度;
n——表数据长度。
MCKD算法相关峭度的定义为:
(2)
式中:T——冲击信号的周期;
N——数据长度点数;
yn——包含故障分量的信号;
M——位移数。
为了求取最优滤波器系数f,使CKM(T)取最大值,令
(3)
滤波器可表示为矩阵形式,如式(4)所示。
(4)
其中
r=[0,T,2T,…,mT]
将得到的最终迭代滤波器系数代入式(1),即可得到冲击信号y。
1.2 改进最大相关峭度解卷积
使用MCKD进行信号处理时,需利用先验知识确定周期参数T。人为经验因素的制约使得MCKD算法在实际应用中有一定的局限性,特别是参数选取不当时,会造成误诊现象。在改进MCKD方法中,原始信号x采用Hilbert变换得到包络信号x(t),通过自相关函数的定义,包络信号x(t)通过自相关函数最大值位置找到信号的冲击周期。自相关函数可定义为:
(5)
式中:t——时间;
τ0——平移系数。
通常在式(5)中τ0=0时,rxx(0)取得全局最大值,显然τ0=0不能用作信号的周期。当式(5)取得最大值时,将平移系数τ0记为τmax,则信号的冲击周期为T=τmax,在迭代过程中,通过不断更新周期,逐渐逼近真正的故障周期。
改进的MCKD方法的目标函数双向重构准则的相关峭度如式(6)所示。
(6)
式中:ynyLT——一次向左循环重构;
ynyRT——一次向右循环重构。
求解滤波器系数等价于求解最大极值问题,即
(7)
根据式(6)和式(7)进行求导运算,首先对分子进行求导,并将dyn/dfk=xn-k+1代入式(7),化简后可得:
yn(yLTxn+LT-k+1+yRTxn-RT-k+1)]
(8)
按照同样方法对分母进行求导,可得
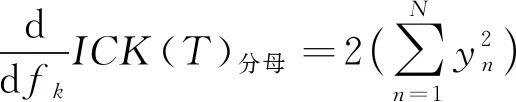
(9)
根据分子、分母求导结果可得最终导数表达式为
+yn(yLTxn+LT-k+1+yRTxn-RT-k+1)]
(10)
令式(10)等于0,并转化为矩阵形式,可得
‖y‖-4(X0(α0L+α0R)+XLTαLT+XRTαRT)
-2‖y‖-6(‖βLT‖2+‖βRT‖2)X0y=0
(11)
其中
βLT=[y1y1+LT,y2y2+LT,…,yNyN+LT]T,
βRT=[y1y1-RT,y2y2-RT,…,yNyN-RT]T,
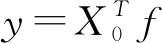
(X0(α0L+α0R)+XLTαLT+XRTαRT)
(12)
改进MCKD算法的步骤如下:
1) 输入原始信号x,采用自相关函数计算包络信号x(t),确定信号周期T;
2) 初始化滤波器系数f=[0,0,…,1,-1,…,0,0]T;
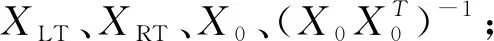
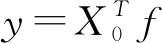
5) 通过自相关函数计算包络的输出信号y及更新周期T、滤波器系数f;
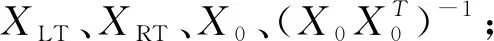
7) 重复4)~6)直到ICK(T)最大时,迭代停止,此时的计算结果即为滤波器系数f及输出信号y。
2 精细复合多尺度模糊熵
2.1 多尺度模糊熵
多尺度模糊熵计算步骤如下:
1) 以嵌入维数m、相似容限r和粗粒化长度为N的原始序列{x1,x2,x3,…,xN},建立新的粗粒向量,即
(13)
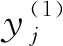
2) 计算每一个粗粒序列的模糊熵,即多尺度模糊熵,如式(14)所示。
MFE(x,m,n,r,τ,N)=FE(yτ,m,n,r,Nτ)
(14)
多尺度模糊熵可以表征不同时间尺度下故障信号的特征,可以有效地解决使用单一模糊熵值衡量时间序列时存在的特征单一问题【12】。但是该算法容易丢失数据,致使计算得到的熵不够准确。
2.2 复合多尺度模糊熵
复合多尺度模糊熵计算步骤如下:
1) 对于时间序列{x(i),i=1,2,…,N},采用式(15)进行粗粒化处理,即
(15)

(16)
CMFE能够整体表征出同一尺度下全部粗粒化序列的模糊熵信息,因此计算结果相比于MSE会更加符合规律。但是,在短序列的计算过程中熵值的未定义概率增大,致使熵值不够准确。
2.3 精细复合多尺度模糊熵
RCMFE改变了CMFE中先求出熵值后再计算平均值的模式,而是先求出尺度因子τ下所有粗粒序列后再求和,然后求得总和的模糊熵。定义RCMFE为:
(17)
2.4 参数设置
首先为RCMFE设置4个参数,即嵌入维数m、模糊函数的梯度n、相似容限r及尺度因子τ。
随着嵌入维数m增大,重构系统的动态过程趋于细致,从而可以获取更多的信息。但同时,随m值的增大,在计算时所需要的数据长度会快速增加,选择过大的m值可能会导致无法提供足够数据的情况。因此,在数据长度有限的情况下,本文取m=2。
在模糊函数中,相似容限边界的梯度值取决于模糊函数的梯度n。而n在向量间的相似性计算中起着权重的作用,随着n的增加,梯度值增加。但是过大的n值会导致细节信息丢失,当n趋于无穷大时,边缘的细节信息会全部丢失。因此,为了保留更多的细节信息,本文取n=2。
若相似容限r过小,则计算结果对噪声较敏感;而r过大,则会致使信息损失,且信息的损失量随着r的增大而增大。经验表明,r的取值范围通常为0.1~0.25SD(SD为标准差)。本文中r=0.15SD。
尺度因子τ决定时间序列粗粒化分割的数量,为便于精细复合多尺度模糊熵值的计算,本文取τ=20。
3 往复压缩机故障特征提取实验
3.1 故障实验研究
本文的实验数据来源于某天然气公司2D12-70型往复压缩机, 在实验过程中, 模拟了阀有缺口、 阀片断裂和阀少弹簧3种常见气阀故障。该压缩机电动机转速为496 r/min, 采样频率为50 kHz。分别用加速度传感器采集进气阀4 g位置的3种故障状态和正常状态的振动信号,测点设置在阀盖上,如图1(a)~图1(b)所示。
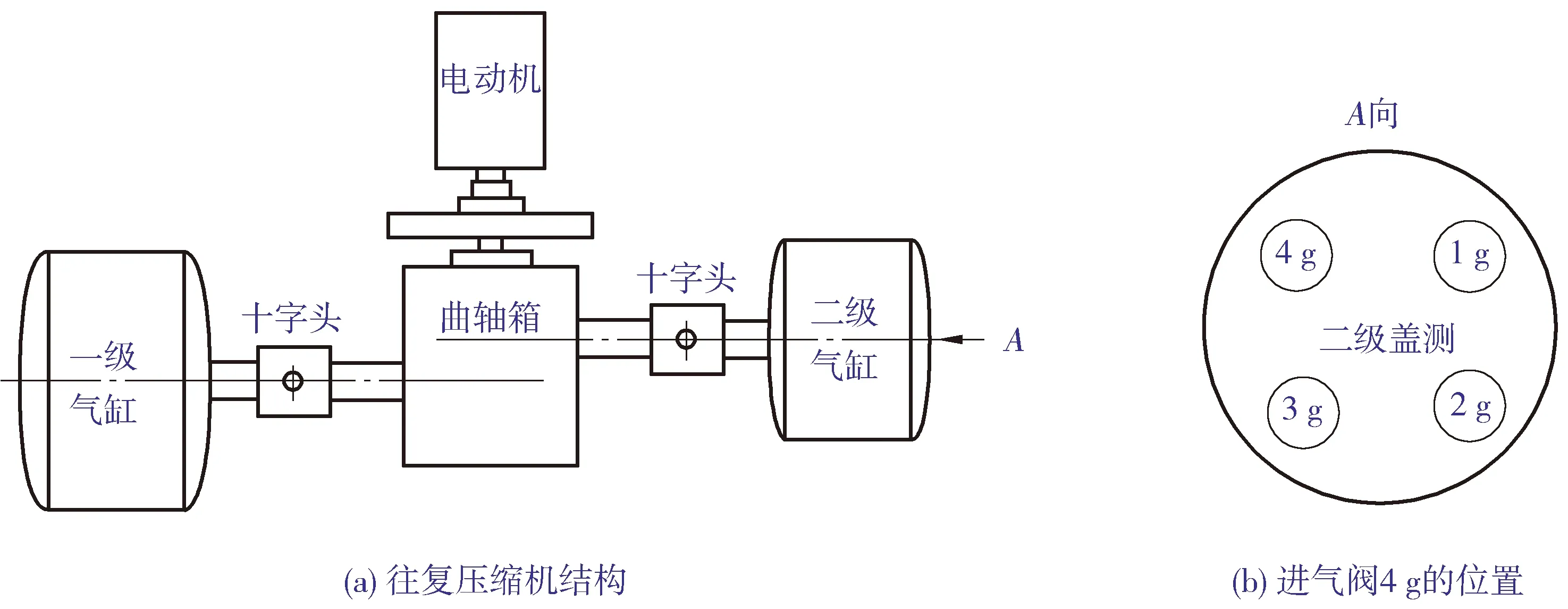
图1 往复压缩机结构及测点位置
其正常状态气阀的时域波形如图2所示,阀有缺口故障时气阀的时域波形如图3所示。由图2 和图3可知,其振动信号的时域波形中存在着大量的背景噪声和其他干扰冲击成分。
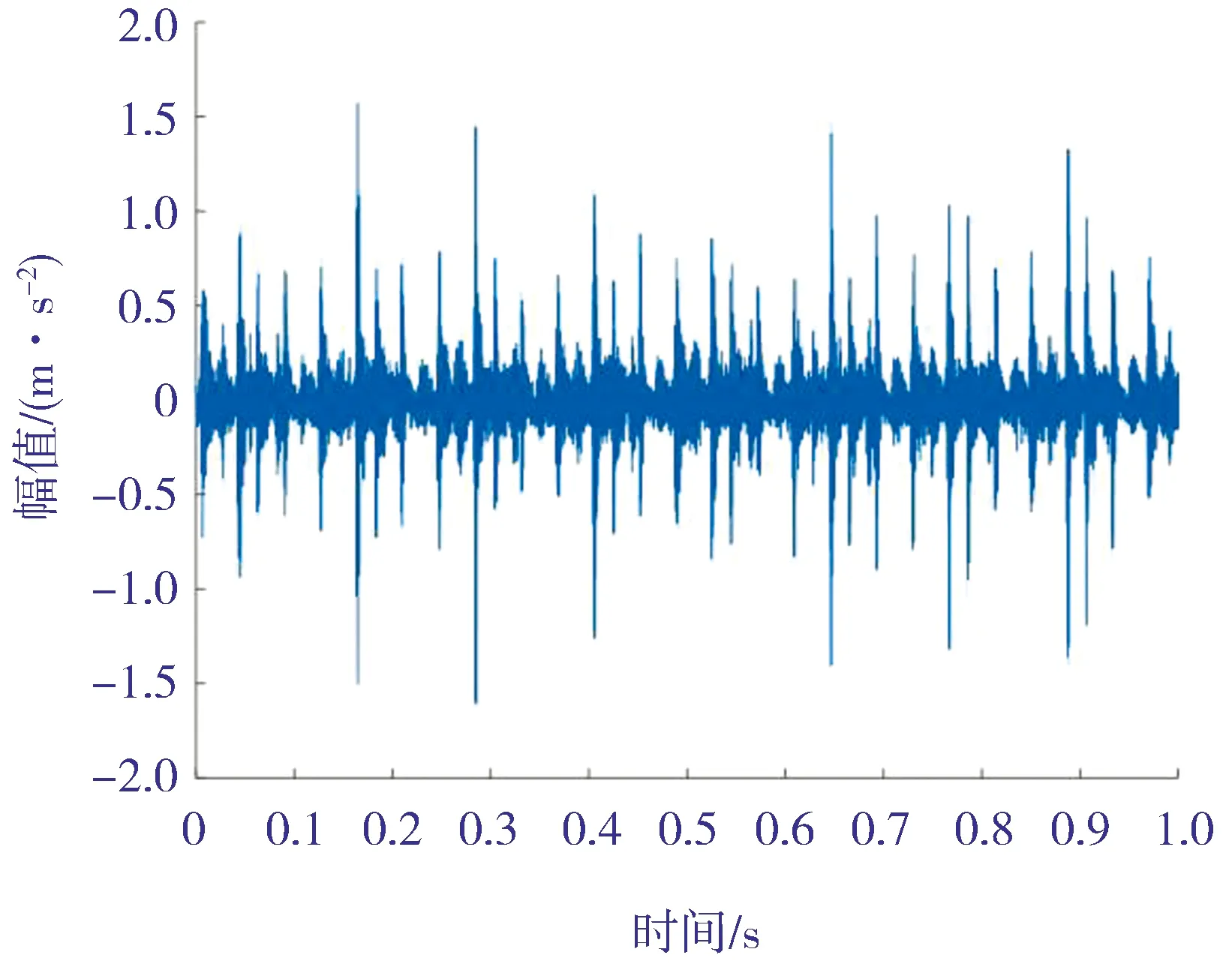
图2 正常状态气阀的时域波形
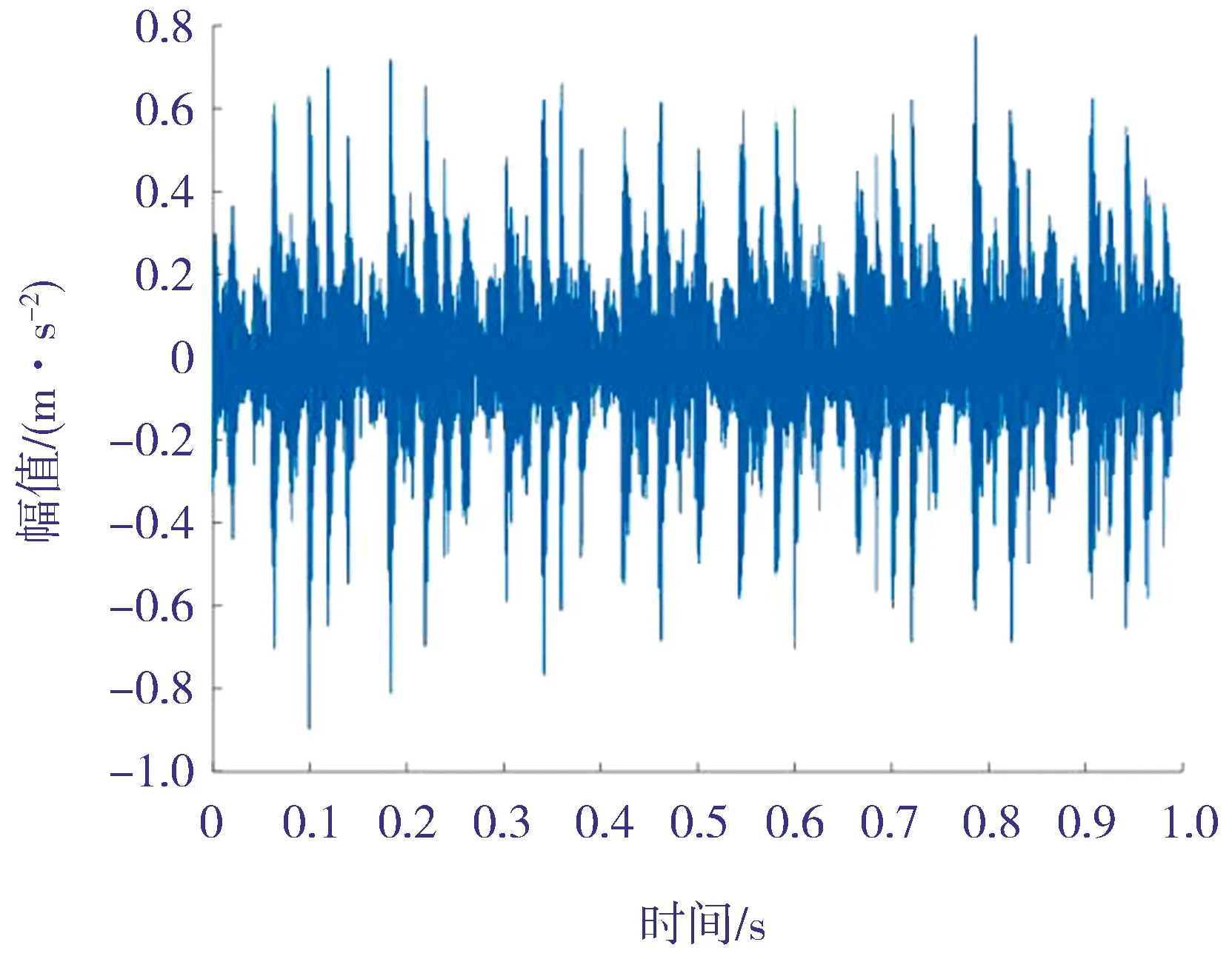
图3 阀有缺口故障时气阀的时域波形
3.2 改进最大相关峭度解卷积及特征提取
以阀有缺口故障为例,选择时长为1 s的数据(N=50 000),设置滤波器长度L=30,对该故障信号进行改进最大相关峭度解卷积处理,结果如图4所示。
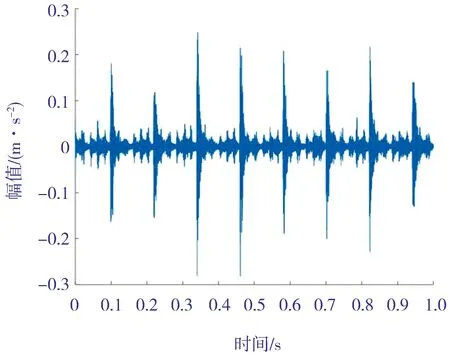
图4 经改进MCKD处理后阀有缺口故障信号时域
阀有缺口故障振动原始信号及经改进MCKD处理后的信号的包络谱如图5(a)~图5(b)所示。观察可知: 在原始信号包络谱中, 故障特征完全淹没于噪声及各种干扰成分之中;而经过改进的MCKD处理后,其包络谱在8.3 Hz处出现清晰的最大幅值点。这正是由于二级气缸内活塞在膨胀过程中,阀片缺口故障使得气阀出现泄漏,从而导致气阀延迟打开而引起的故障冲击现象,说明改进MCKD能有效地滤除噪声、突显故障冲击特征。
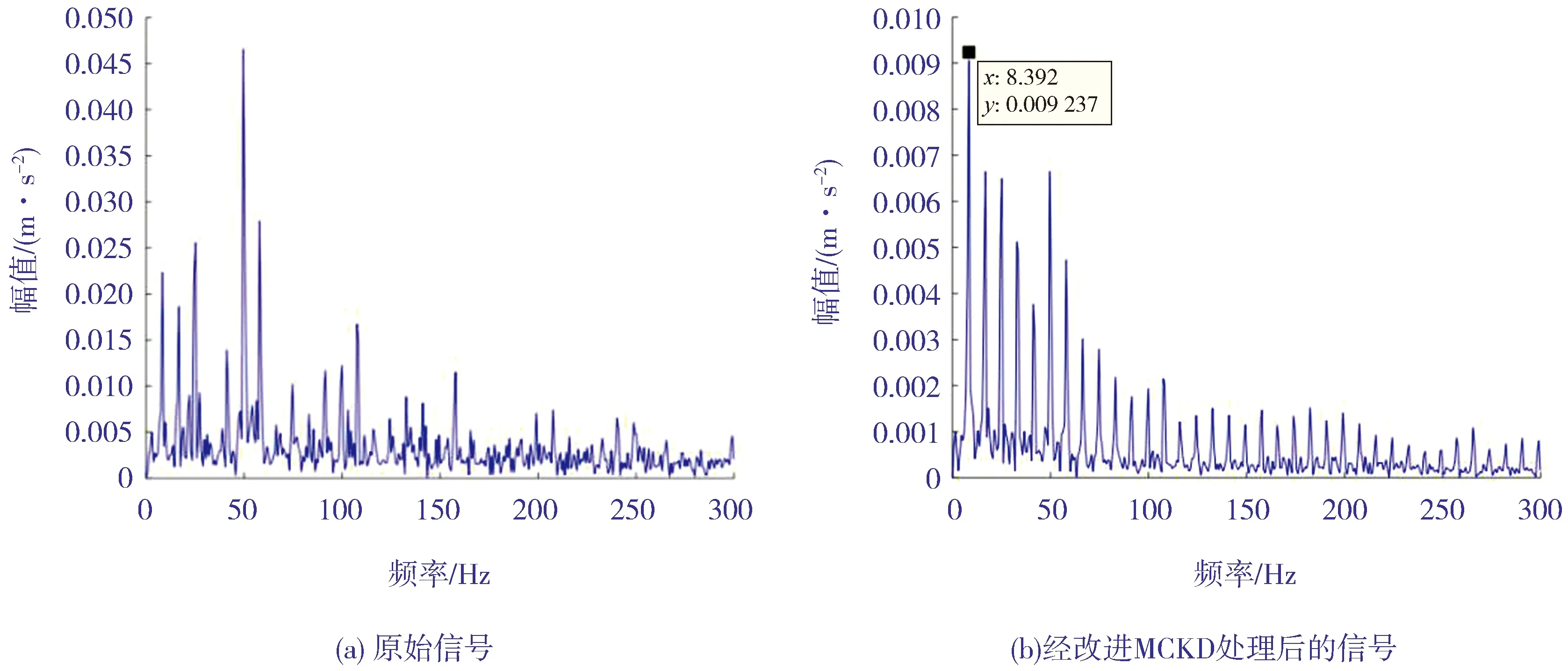
图5 阀有缺口故障信号的包络谱
设置嵌入维数m=2、模糊函数的梯度n=2、相似容限r=0.15SD、尺度因子τ=20。选择上述3种故障及正常工况振动信号进行改进解卷积(MCKD)处理,然后分别对每种工况解卷积后的信号进行精细复合多尺度模糊熵值(RCMFE)计算,得到如图6所示的气阀4种状态的RCMFE曲线。由图6可以看出,4种气阀状态下的 RCMFE 具有较好的可分性。因此,选取气阀4种工况信号的RCMFE值作为往复压缩机气阀故障诊断的特征向量。
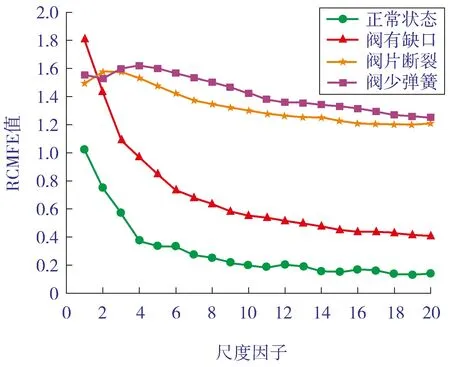
图6 经改进MCKD处理后不同工况振动信号的多尺度模糊熵值
3.3 故障识别结果对比分析
为验证本文方法对往复压缩机气阀故障诊断识别的有效性与优越性,采用改进最大相关峭度解卷积与精细复合多尺度模糊熵相结合的方法,分别提取正常工况及3种气阀故障工况振动信号特征向量,然后使用支持向量机(SVM)进行训练和特征识别。
提取正常工况及3种气阀故障工况振动信号的特征向量数据各120组,将每种状态的80组作为训练样本,剩下的40组作为测试样本,利用SVM进行故障识别。采用不同方法的识别准确率如表1所示。对各个工况数据进行对比分析,发现本文采用的改进方法优于原始方法。
4 结论
研究了基于改进MCKD与RCMFE相结合的气阀故障诊断方法,并成功地将其应用于往复压缩机气阀不同工况的特征提取。通过模拟气阀故障实验,并对实测数据进行分析,结果显示,该方法可有效提取气阀故障特征。
1) 将自相关函数和双向重构准则的相关峭度应用于MCKD的改进,能够更准确地估计故障周期,突出故障冲击特征,从而准确地提取故障状态的瞬态冲击响应。
2) 经RCMFE多尺度模糊熵度量信号的复杂程度,构造状态特征向量,能够准确地提取气阀的故障特征信息。
3) 将改进MCKD与RCMFE算法相结合并成功地应用于往复压缩机气阀故障诊断中,故障识别准确率结果表明:该方法作为往复压缩机气阀故障诊断的一种新方法,具有较高的故障识别率。
