热交换器胀管工艺的优化及探讨

李爱国，林雅岚，祁少昆,党亚茹

(陕西化建工程有限责任公司，陕西 咸阳 712100)

管壳式热交换器管板和换热管的连接接头形式及质量优劣是影响设备运行寿命的重要因素。在强度焊+贴胀连接结构中，贴胀的目的是通过胀接来填充换热管和管孔之间的间隙，以减小换热管在设备运行过程中因振动而对焊接接头造成影响，同时也兼备一定的密封及抗间隙腐蚀的作用。

胀接一般通过测量及计算胀管率来进行控制，必要时也要求制造前进行胀管工艺评定。笔者认为还存在以下问题需要探讨：

1) 实际采购的材料在力学性能方面和材料标准中给出的性能指标差异较大，用材料标准中屈服强度下限值计算得到的胀接压力是否能够达到预定的胀管效果？

2) 胀管工艺评定需要在设备制造前进行，要提前购买材料，且评定需要做许多检测项目，耗时比较长，所以对单台设备制造也不太适合。

3) GB/T 151—2014中对强度胀接仅提到换热管材料的硬度应低于管板的硬度，对于贴胀工艺方面鲜有指导条款【1】。且工程中经常出现不同材料搭配，不一定能够满足这个硬度匹配条件，例如，同种材料牌号的换热管和管板搭配因为钢管和锻件的力学性能差异就可能出现相反的匹配，甚至会出现换热管硬度及强度比管板高许多的情况，如双相钢或镍基合金换热管和低合金钢管板的匹配。

理论上讲，对高硬度材料的换热管进行退火或者二次固溶处理从而达到降低硬度并满足胀接要求的原理是可行的，是一般的解决方式。但实际上，硬度和强度的关系不是非常确定，且小直径换热管及管孔内壁硬度的测量难度和误差非常大，只采用硬度值来判定换热管、管板材料强度的匹配不是理想的解决办法。

1 分析步骤及方式

为解决上述问题，从理论上进一步探讨胀接的基本原理，借助应力分析软件模拟胀管过程，对拟定的胀接工艺进行验证，确定出合适的胀管压力，从而提高胀管一次成功率，简化工作程序，保证胀接质量。

本文将按照以下步骤展开分析：

1) 利用应力分析软件ANSYS对胀接过程进行仿真建模；

2) 按照材料理论屈服强度及材料实际屈服强度分别确定胀接压力进行模拟仿真计算，然后进行比较；

3) 建立分析模型时，分别按管桥等效圆筒的单管胀接模式及多管胀接的实际模型模式两种情况进行分析，然后对结果进行比较；

4) 对于偶尔会出现的管孔偏差超标引起间隙过大的情况也进行了模拟分析；

5) 按照胀接仿真模型参数进行实际胀管试验，并对试验结果与计算机模拟结果进行比较。

2 建模及分析过程

2.1 单管胀接(等效圆筒理论)的仿真模型

管板和换热管的胀接过程属于几何非线性及材料非线性的结合，属于弹塑性理论范畴，涉及材料加工硬化以及从非接触到接触阶段的过渡，从加载、保压到最后卸载，计算过程比较复杂，如果对整个管板建模进行分析，又会涉及管孔之间的干涉，常常导致结果很难收敛，且计算耗时很长，非常困难。经查阅资料，对管桥部分进行简化。依据等效圆筒理论，先对单管和等效成圆筒的单个管桥建立模型，采用V.MESSIS屈服准则，简化运算；然后再建立管板一个局部的模型，包含至少9根管子，基本能够代表实际管板情况；最后对运算结果进行对比，总结出工程上简单易操作的模拟分析模式。

2.1.1 等效圆筒外径计算

运用Kohlpaintner 的计算公式【2】进行计算，其等效原则是换热管外壁的位移相同，比较贴合工程实际，计算也较简单。

-2.433 88η2+1946 83η+0.980 34

(1)

式中：Ds——等效圆筒外径，mm；

p——换热管中心距,mm；

η——管桥系数,0.11≤η≤0.63。

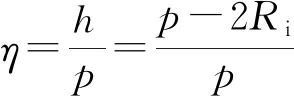
(2)

式中：h——沿两孔中心线的管桥宽度，mm;

Ri——管孔内半径,mm。

根据式(1)和式(2)计算得知：对于φ19×2 的换热管，Ds=34.86 mm；对于φ25×2.5 的换热管，Ds=43.46 mm。

2.1.2 双相钢S22253 材料非线性(应变强化段)数据的获取

由于ANSYS的材料库中无S22253 双相钢钢管材料的非线性阶段数据，因此对钢管取样进行了拉伸试验，经过曲线回归和线性化处理得到屈服阶段线性化曲线，结果如图1所示。然后在ANSYS软件里自行建立了S22253 钢管材料的非线性阶段的数据，为进一步分析奠定基础。

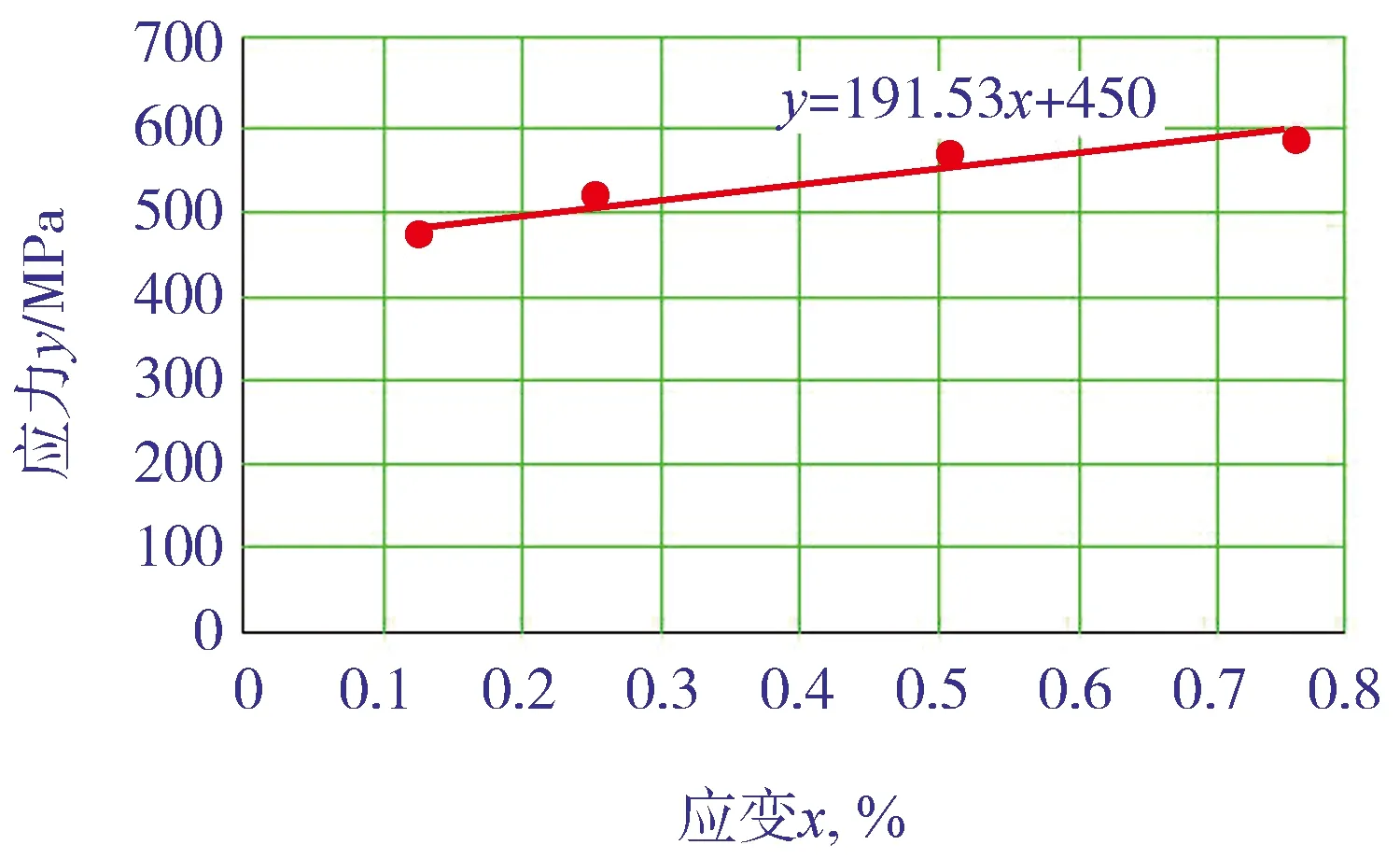
图1 S22253钢管屈服阶段线性化曲线

2.1.3 胀接压力确定

为了达到胀接的效果，一般初定的胀接压力需大于消除换热管和管孔之间间隙所需的压力，并小于管板弹性极限对应的压力，无论如何，最大极限压力应不得使管桥部分(等效圆筒)发生全部屈服。

经查阅资料，目前计算胀管压力的公式有王海峰、颜惠庚等基于弹塑性理论并采用假想等效圆筒的几何模型推导出的公式，但二者差异比较大【2】。王海峰的推导公式考虑了变形时的幂应变强化特性，比较科学，但是非常复杂，不适合工程实际应用【3】。

本文采用大洋胀管机厂提供的公式计算初设胀管压力(该公式其实是在颜惠庚的公式中加入了考虑周围其他换热管影响的内压放大系数)。胀管压力初定结果见表1。

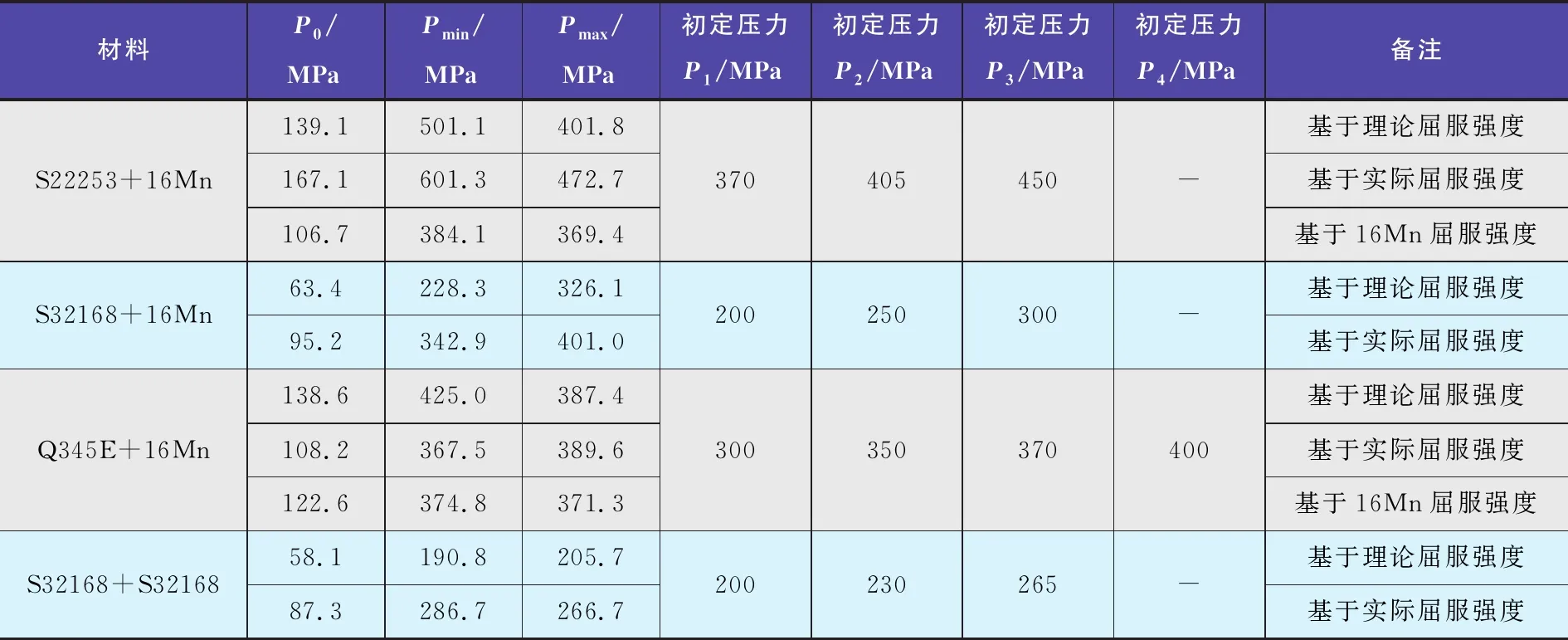
表1 胀管压力初定

先按胀管机厂给出的公式进行计算，再按材料标准强度下限及材料实际力学性能两种材料模型进行仿真和试验。

2.1.4 单管胀接计算机模拟仿真过程(等效圆筒理论)

胀接属于静力学中非线性弹塑性分析，本文采用ANSYS Workbench 16.0中 Static structural模块进行了3D建模。对于1根换热管和套在外面的1个等效圆筒的组合，因加载区域需要，将换热管分为3部分并建立组件；为了简化运算，沿XZ及YZ平面进行了对称设置，模型便简化为1/4 ；为了方便查看计算结果，分别建立了沿换热管和圆筒壁厚方向的2个路径，并建立了换热管外壁的假想构造面(查看结合面残余剪应力及正应力)，同时建立了以换热管内孔为基准的柱坐标系，网格划分时沿换热管壁厚分为3层，等效圆筒沿壁厚分为5层，其余均为系统自动划分的六面体单元，可以满足后续分析的需要。换热管和管孔的间隙按照GB/T 151—2014中Ⅰ级管束要求，换热管外壁和管孔间设定为摩擦接触，摩擦系数取0.15，粗糙度取Ra6.3。

换热管内孔相应区域加载初定的胀管压力，将管板一端面(垂直于换热管)设置成固定约束，相应的换热管同一端也设定为固定约束，管板另一端面及换热管另一端设置成轴向位移等于零，1/4 剖切面设置成对称约束。

求解过程分为3步，每步又分为20个子步，加载阶段2 s，保压阶段4 s，卸载阶段2 s，并关闭软弹簧及系统自定的分步。

按照工程常用的几种管板与换热管的材料搭配[包括双相钢+低合金钢、奥氏体不锈钢+低合金钢、低合金钢+低合金钢(同牌号)、奥氏体不锈钢+奥氏体不锈钢(同牌号)]分别进行仿真分析并进行了比较，材料性能见表2。

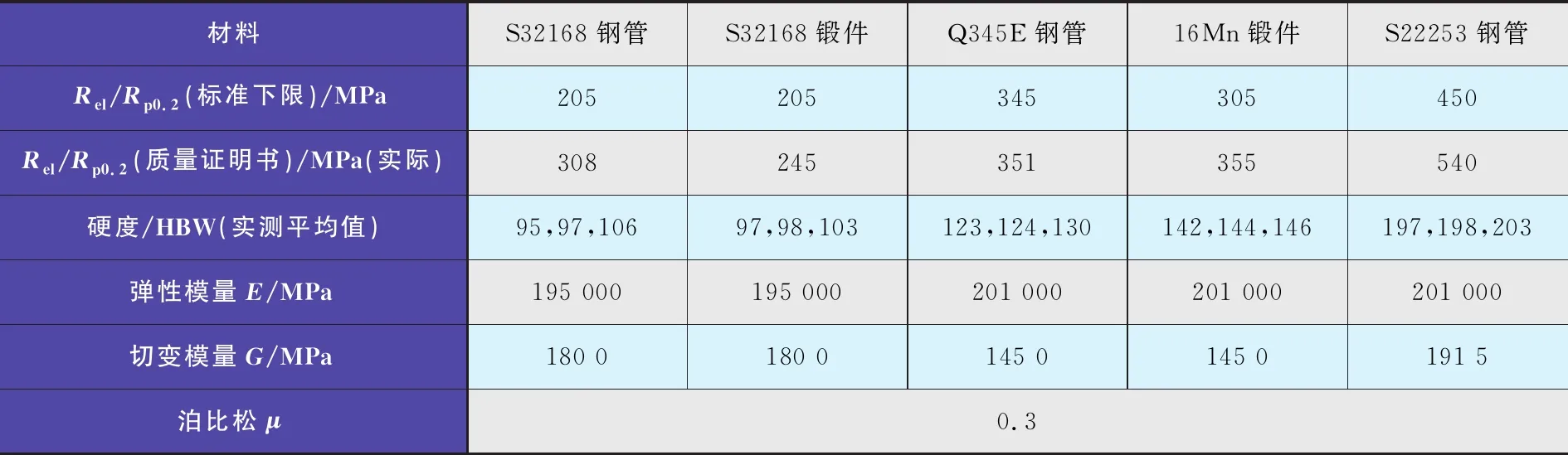
表2 材料性能列表

2.1.5 单管胀接计算机模拟仿真结果

摘录ANSYS建模及加载分析的两个算例结果(见图2和图3)。由图2很容易看出， 在合适的胀管压力下(第一算例)卸载后， 管桥的等效圆筒最大径向应变发生陡降，而换热管的最大径向应变几乎与加载期间相同，结合面的最小正应力(法向)陡升，接触面同时产生了较大的残余剪应力。这一现象证明，管桥等效圆筒径向变形大部分属于弹性，卸载后残余变形很小，而换热管的径向变形几乎完全属于塑性，残余变形很大，结合面残余正应力增大并产生了很大的残余剪应力。

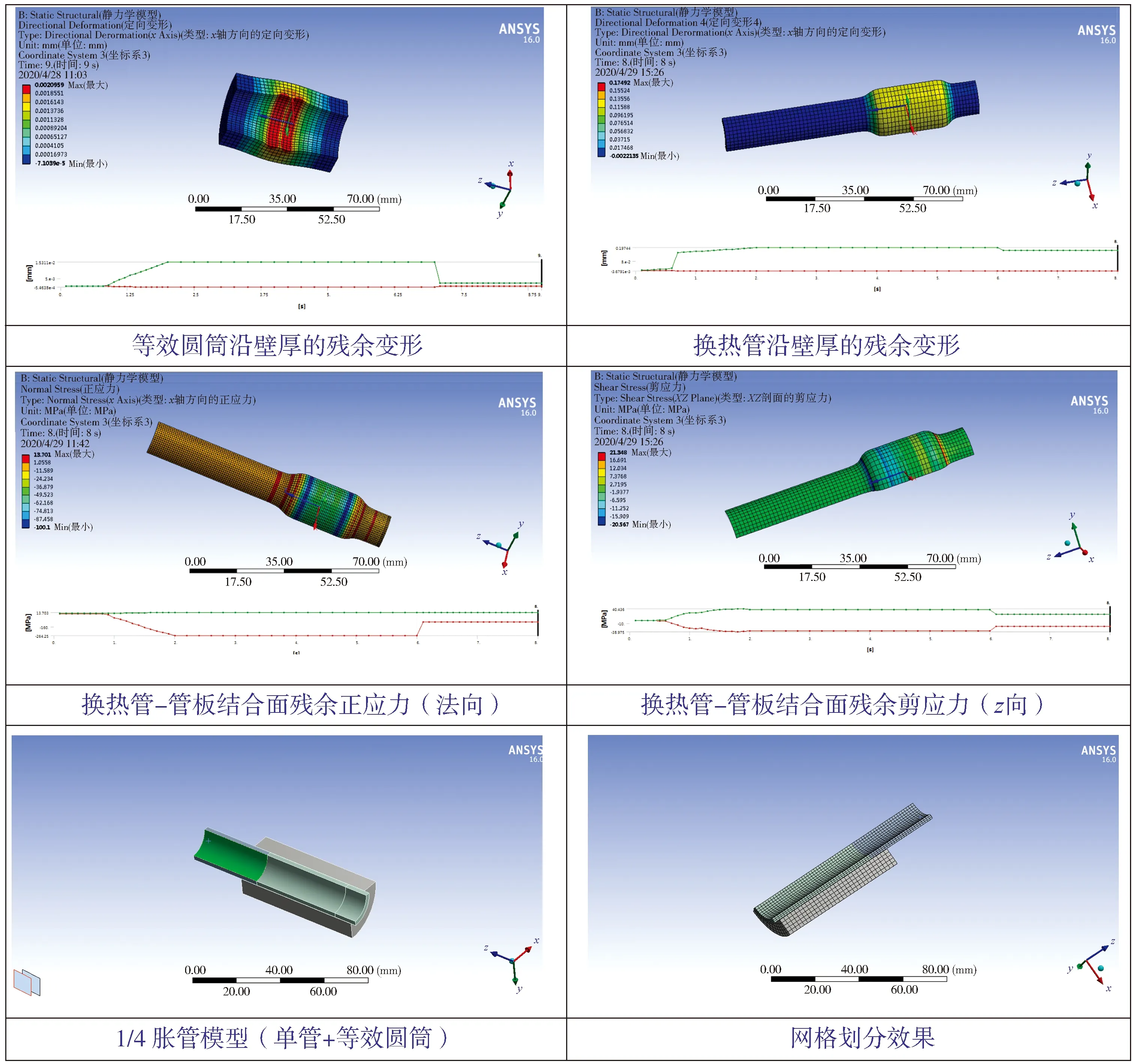
图2 ANSYS模拟仿真分析(较合适胀管压力下的胀管效果)

从图3(第二算例)可以看出，在较大胀管压力下，对比管桥等效圆筒的径向残余变形，二者几乎全部为塑性变形，没有回弹，结合面不能产生足够的正应力及剪应力。

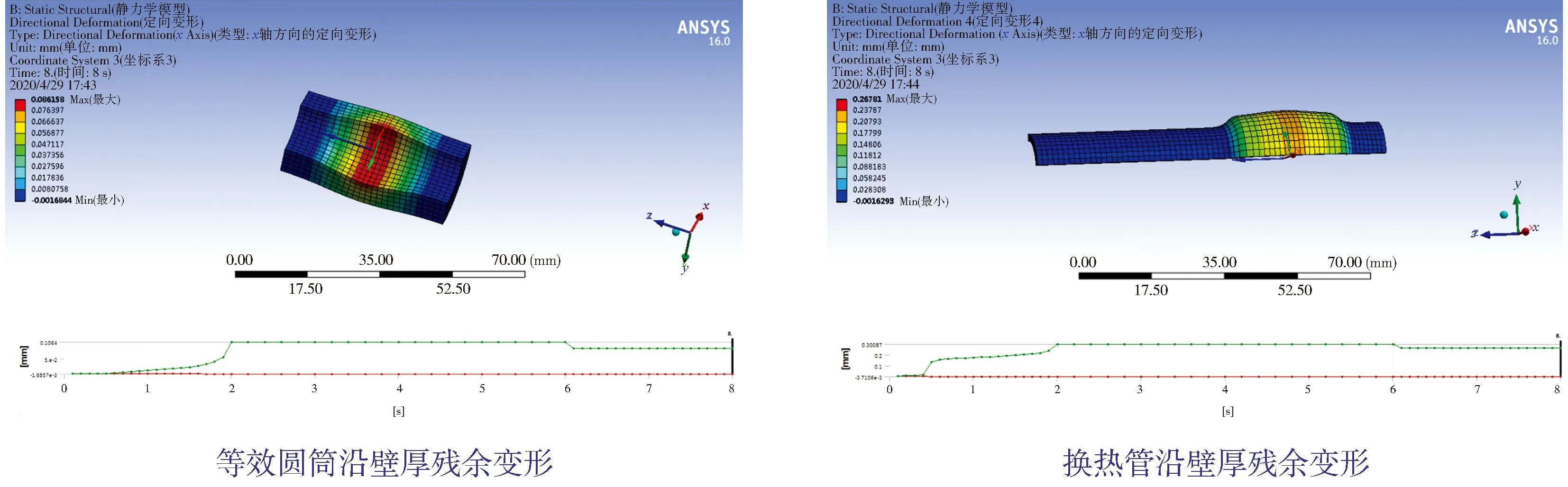
图3 ANSYS 模拟仿真分析(较大胀管压力下的胀管径向残余变形)

2.1.6 表3～表6分析结果小结

表3～表6分别列出了4种不同换热管材料(管材)与管板材料(板材)搭配模型的ANSYS分析结果，小结如下：

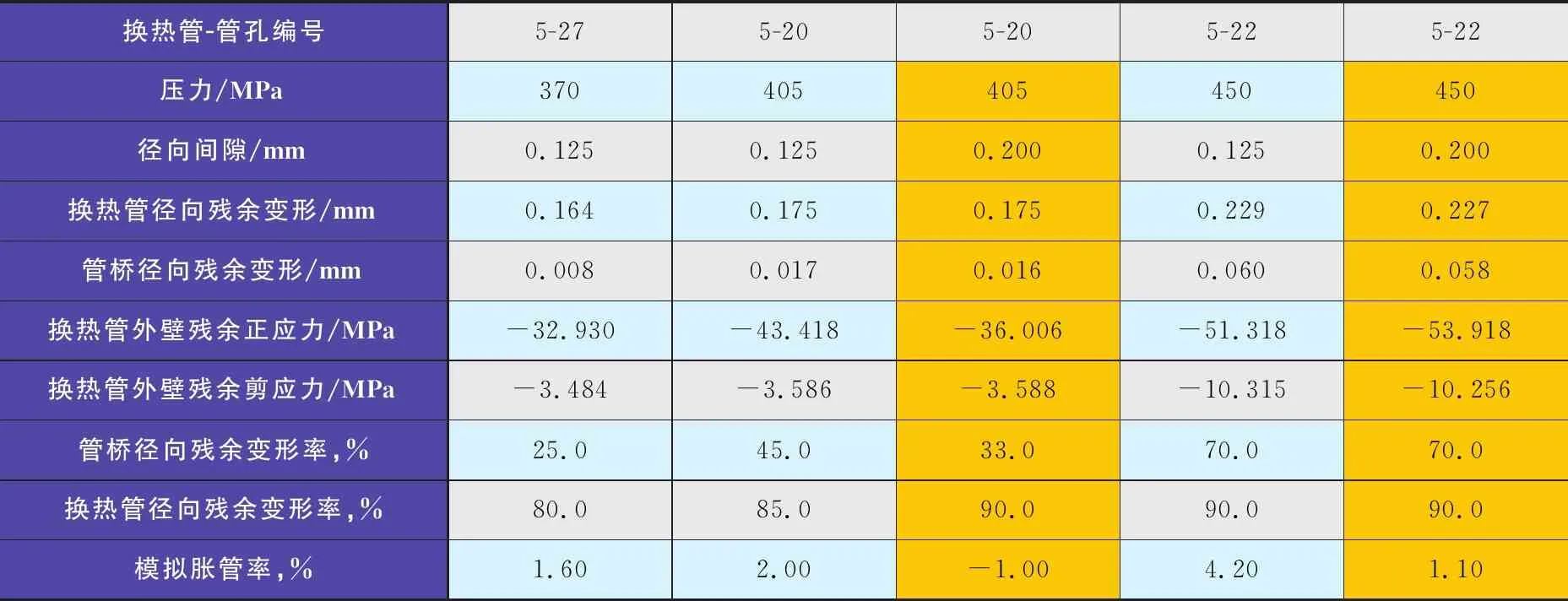
表3 ANSYS 分析结果(模型一：管材S22253+板材16Mn)

表4 ANSYS 分析结果(模型二：管材S32168+板材16Mn)

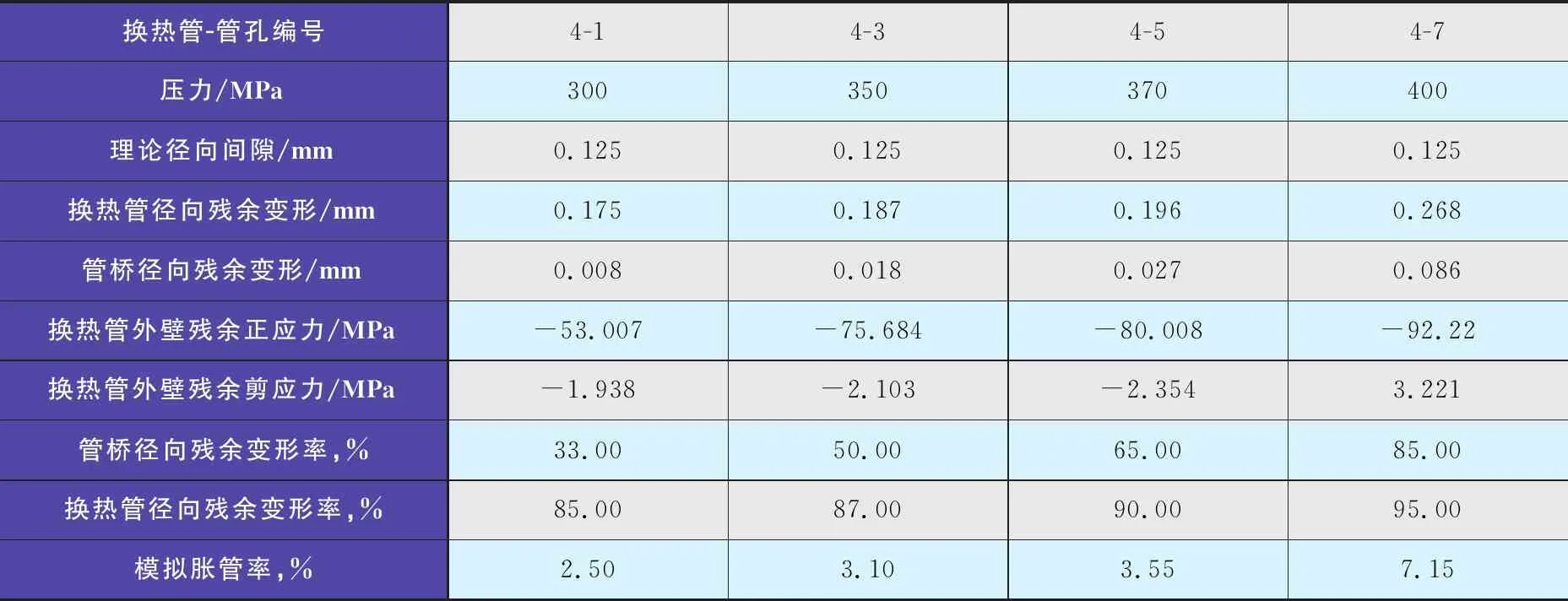
表5 ANSYS分析结果(模型三：管材Q345E+板材16Mn)

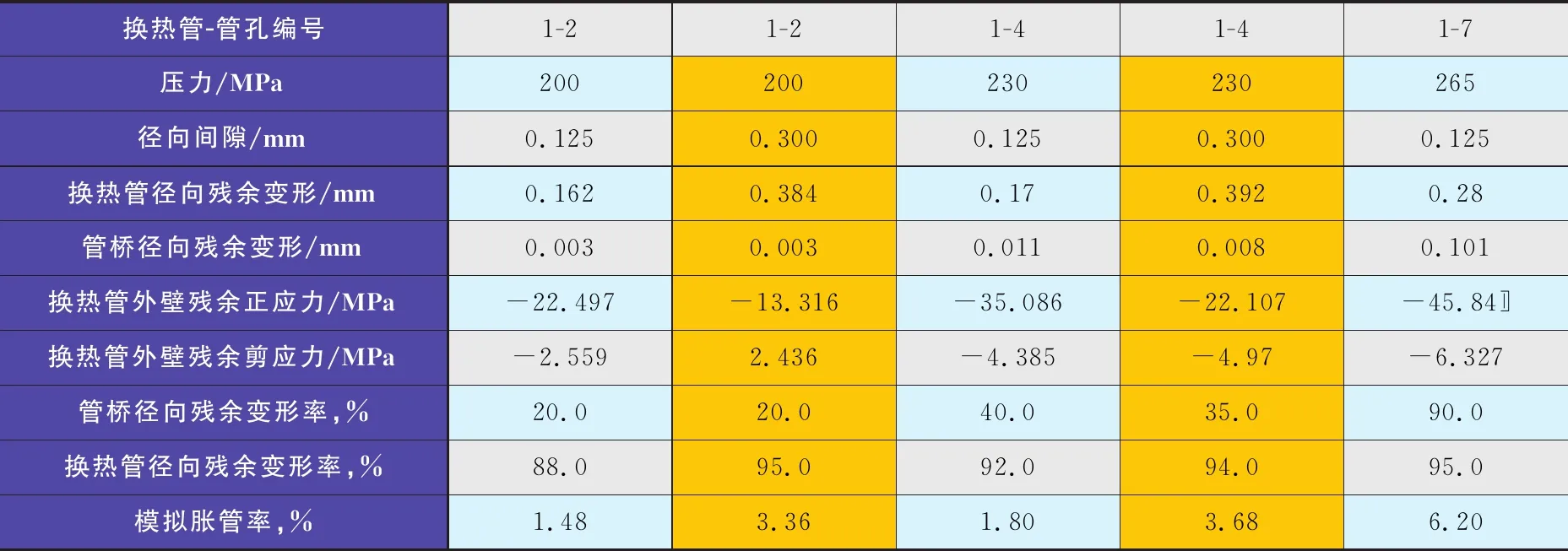
表6 ANSYS 分析结果(模型四：管材S32168+板材S32168)

1) 在初定的各组胀接压力下，换热管径向残余变形都大于管孔和换热管的径向间隙，除了换热管减薄外，径向残余位移已经填满了间隙。

2) 随着胀接压力的增加，换热管径向残余塑性变形在增大；等效圆筒的径向残余塑性变形也在增大，且在某一临界压力下发生陡增，此时管桥陷入大面积的塑性变形。

3) 模拟仿真的胀管率(壁厚减薄率)范围在 1.2%～7.0%，可以满足贴胀的要求。

4) 在合适的胀接压力下，换热管几乎全部发生了塑性变形，而管桥的等效圆筒只发生了少量的塑性变形，其结合面产生了残余法向压应力及轴向剪应力，不但填满了间隙，而且为抗拒一定的拉脱力奠定了基础。同时也能看到，当胀管压力增加到一定程度时，虽然胀管率和径向残余变形都非常大，也能填补间隙，但是因管桥发生了大面积的塑性变形，结合面的抗剪切能力并没有提高。同时因胀管率增大是由于换热管壁厚减薄量增大引起的，这势必会牺牲换热管的承载能力，故而增加胀管压力并不是理想的措施。

5) 由以上2个故意放大间隙(黄色区域)的模型的模拟分析结果来看，有如下结论:

a) 对于S22253+16Mn模型，在同样胀接压力(405 MPa)下，换热管径向残余变形变化不大，已经小于管孔和换热管之间的间隙，没有达到胀接效果；而在较大胀接压力(450 MPa)下，换热管径向残余变形可以填补空隙，能够满足胀接的要求。

2. 换热管规格φ25 mm×2.5 mm,管板厚度50 mm，胀接长度25 mm。

2. 换热管规格φ25 mm×2.5 mm，管板厚度70 mm，胀接长度50 mm。

b) 对于S32168+S32168 模型，当管孔偏大时，在初定的200 MPa 及230 MPa胀管压力下胀接，都能达到预期的胀管效果，与理论间隙的情况没有不同，而且胀管率提高一倍左右。

c) 这种大间隙问题出现在管板钻孔时,偶尔会发生个别管孔直径尺寸超差或者仅管板背面部分孔径超差的情况。此时，对于高屈服强度材料换热管，用提高胀接压力来补偿大间隙是可行的；而对于低屈服强度材料(比如奥氏体不锈钢)来说,无需提高胀接压力也能达到胀接目的,但这是以牺牲换热管壁厚为代价的，必要时还需校核换热管的应力情况，所以加工管孔时严格保证图纸要求的公差是非常重要的。

2.2 多孔模型模拟仿真及与单管加等效圆筒变形情况比较

以上对单管加等效圆筒胀接时的受力及变形情况进行了分析，对于多孔(至少1个管孔周围的其他相邻布管都存在)的情况，每1个单孔的变形和受力势必会互相影响。根据有关资料的介绍，只研究某一单孔及其周围相邻其他孔这一局部模型即可，其偏差和实际情况相差不是很大，可以用于工程上的计算。况且换热管的管孔少则几百，多则几千，若用实际模型来计算分析胀接情况，鉴于目前的计算机能力，计算周期将非常长，很难得到收敛解，也无必要性。本文就正方形布孔情况，建立1个管孔及其周围环绕的8个管孔的计算模型，对中心的一个孔进行分析，加载及约束和单孔基本相似，并由此得到了收敛解。现就其中一算例(S22253+16Mn，胀管压力405 MPa)的变形分析结果和单孔进行比较。多孔模型仿真云图见图4。

由图4可以看出，在同样的加载及约束条件下，由于周围管孔的影响，管桥残余变形大幅度减小，换热管径向残余变形也有所减小，但仍能填满换热管和管孔之间的空隙。管桥的残余变形减小证明其弹性变形增大、塑性变形减小，对于胀管的效果是增强的，由此可知，单管加等效圆筒模型模拟仿真结果是偏于保守的，可以用于工程实践。

图4 多孔模型仿真云图

3 实际胀管效果与仿真模拟结果比较

3.1 胀管工艺试验步骤及要求

根据设定的模型，按照计算初定的和模拟仿真相同的胀管压力，对以上4组材料的组合进行了实际胀管试验。试验步骤不再赘述。将胀接部分剖开，观察结合面贴合情况，结果显示，贴合效果非常好(见图5)。

图5 实际胀管及拉脱力试验

3.2 胀管工艺试验结果分析及与模拟结果比较

由试验结果可知，前3组材料配合，实际胀管率略低于模拟胀管率(个别情况最大胀管压力下，实际胀管率大于模拟胀管率)。这是因为，一方面由于管孔允许偏差的原因，实际间隙出现大于模拟分析时的理论间隙，钢管径向整体位移增大，故而胀管率(壁厚减薄率)减小；另外，实际胀管试验加载的胀管压力是考虑了多孔影响之后计算初定的，故而单管计算机模拟时变形较大，而实际胀管时是多孔，变形较小。

最后1组材料因管孔加工超差，即使在胀管压力不变的情况下，胀管率也会陡然增大。这可以证明，对于奥氏体不锈钢这种材料组合，要达到胀管效果是非常容易的，但是间隙过大是以牺牲换热管壁厚为代价的，必要时还需考虑换热管本身的应力情况，所以制造时保证管孔的尺寸精度非常重要。

4 结语

通过计算机建模仿真分析及实际胀接试验，验证了按照修正后的颜惠庚基于理想弹塑性力学模型计算出的初定压力，在工程实践中应用是基本符合要求的，但要分以下2种情况分别进行处理：

1) 对于能符合胀接基本原理(换热管屈服强度及硬度低于管板的情况)的材料组合，无须考虑材料的实际力学性能和标准下限的差异度，直接以标准下限值代入计算，即可得到满意的贴胀效果；按较小的强度差匹配即可。

2) 对于不符合胀接基本原理的材料组合，要根据经验初定胀管压力。确定原则是最大胀管压力不能使管板应力超过管板的实际弹性极限值。然后利用计算机模拟仿真(单根换热管加等效圆筒或者局部多孔模型，用材料的实际力学性能进行模拟)找出合适的胀管压力即可，可以不进行实际的胀管评定；但对于重要设备及重要材料(如加氢反应器，S22053、S22253换热管)，最好再辅助进行胀管工艺评定，以确保产品胀接质量。