高参数热力设备中临界热流密度预测模型研究
2021-11-23林睿南安建川
林睿南, 王 昊, 安建川, 肖 飞, 王 科
(1. 中国石油西南油气田分公司输气管理处,四川 成都 610213; 2.中国石油大学(北京)机械与储运工程学院,北京 102249; 3. 中国石油川庆钻探工程公司地质勘探开发研究院,四川 成都 610051)
沸腾换热装置广泛存在于石油、化工等工业领域中。流动沸腾时,壁面液体强烈蒸发,过度汽化使得壁面液相的消失,造成壁面温度突升,且热壁面几乎全部被高温蒸汽覆盖,导致传热恶化的发生,此时对应的热流密度叫做临界热负荷(简称CHF)。在非绝热系统内,加热使得管内液相份额逐渐减少,气相份额逐渐增多,导致流道内产生各种流型。在均匀加热竖直上升管内,传热区域可以分为单相流动区、过冷区和饱和沸腾区。通常在饱和沸腾区内,气液两相流型可以分为泡状流、弹状流、搅拌流和环状流。
针对干涸型CHF的研究中,环状流液膜蒸干的假说被广泛接受,其中以液膜流动模型的应用最为广泛。在非绝热系统环状流内,气液界面同时存在液滴夹带、沉积和蒸发等传质过程。液滴通过夹带脱离液膜进入气相场,同时夹带液滴受气相场湍流脉动的影响重新沉积到液膜表面,且由于加热使得一部分液体蒸发,因此在夹带和蒸发作用下,液膜流量沿流动方向不断减小,当壁面液膜流量减小为零或者接近零时即达到临界热流密度。计算临界热流密度通常采用Whalley等【1】提出的环状流液膜流动模型,其计算控制体如图1所示,计算表达如式(1)所示。

图1 液膜流动模型计算控制体
(1)
式中:Gf、dT、z、md、me和mv分别为液膜质量流率、管径、轴线方向、液滴沉积率、液滴夹带率和液滴蒸发率。对式(1)从环状流起点到管道出口积分,可以获得环状流内液膜流量沿流动方向的分布。其中环状流起始点处液膜初始流量Gfo可以用式(2)进行计算。
Gfo=G(1-xa)(1-Eo)
(2)
式中:Gfo、G、xa和Eo分别为环状流起始液膜流率、质量流量、环状流起始干度和环状流初始夹带份额。
1 初始夹带份额对临界热负荷预测的影响
由式(2)可知,初始夹带份额Eo直接影响液膜质量流量的初始值。通常Eo通过假设确定,如Hewitt等【2】假设Eo=0.99,Whalley等【1】和Saito等【3】假设Eo=0.9,Govan在不同的研究中分别假设Eo=0.99【4】和Eo=0.91【5】,Okawa等【6-7】假设Eo等于平衡态下的液滴夹带份额。可见,不同学者对于环状流起始点液滴夹带份额假设值均较大,且基于以上假设值采用液膜流动模型均可获得较好的CHF预测结果。然而实验结果表明,夹带份额在搅拌流到环状流转变界限处达到最小值【8-9】,通常为Eo=0.2~0.3。因此,前人对初始夹带份额的假设虽然保证了计算精度,但是缺乏物理意义。
为了研究不同质量流量下初始夹带份额对CHF预测精度的影响,假设初始夹带份额Eo从0.1~0.9等增量(增量为0.1,即Eo分别取0.1,0.2,0.3,…,0.9,下同)变化,并分别代入式(1)和式(2)进行计算。结果表明:当质量流量较小时,初始夹带份额从0.1~0.9的任意取值对CHF计算结果影响均很小;当质量流量较大时,初始夹带份额的变化对CHF计算结果影响非常大,如图2所示。
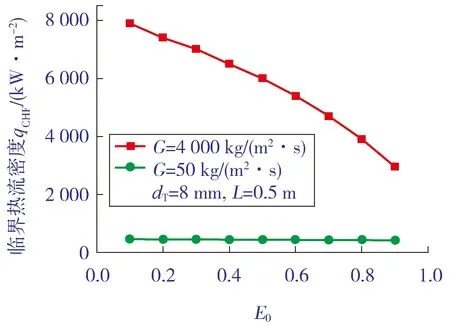
注:L为管道长度。
图3(a)~图3(b)所示为初始夹带份额对干涸点干度x的影响, 同样假设初始夹带份额从0.1~0.9等增量变化。结果表明: 当质量流量较小时, 干涸点处的干度值受初始夹带份额不同取值的影响较小; 当质量流速较大时, 较小的初始夹带份额条件下获得的干涸点干度与较大的初始夹带份额条件下获得的干涸点干度值差距较大。
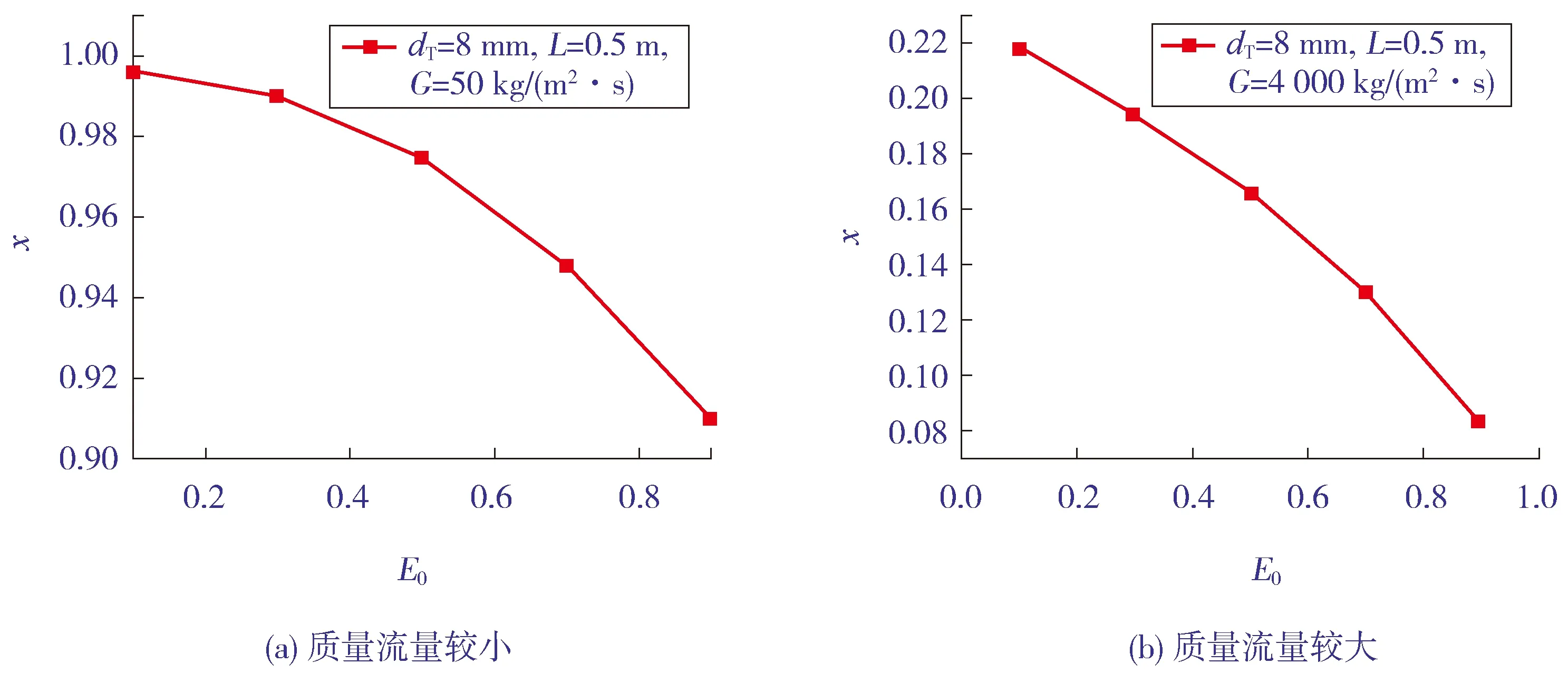
图3 初始夹带份额对干涸点干度的影响
因此,CHF预测精度对环状流起始点初始夹带份额的选取较为敏感,特别是当流量较大时,初始夹带份额对CHF的预测精度有很大的影响。
2 搅拌流内夹带液滴
由于在连续的流型变化中,搅拌流长度通常较短,其内部产生的夹带液滴被气相场携带会对下游产生很大的影响。实验发现,在弹状流向搅拌流流型转变时,液桥崩塌形成较大的液块,导致搅拌流起始点处的液滴夹带份额非常大。大液块在气流的作用下破裂形成小液滴,且部分较大液滴在沉积过程中与液膜撞击造成二次液滴的产生。此外,在搅拌流动中夹带液滴的产生方式同时存在口袋式破碎和丝带式破碎2种方式【9】。与丝带式破碎产生的小液滴相比,口袋式破碎产生的液滴不仅粒径较大,且具有较大的动量。若搅拌流内产生的液滴,尤其是具有较大动量的大液滴进入下游环状流,势必会对环状流内气液相分布产生严重的影响。因此,鉴于流型对CHF的影响,建议将现有的环状流液膜流动模型计算起始点提前至环状流起始点。搅拌流内常见液滴夹带方式如图4(a)~图4(c)所示。
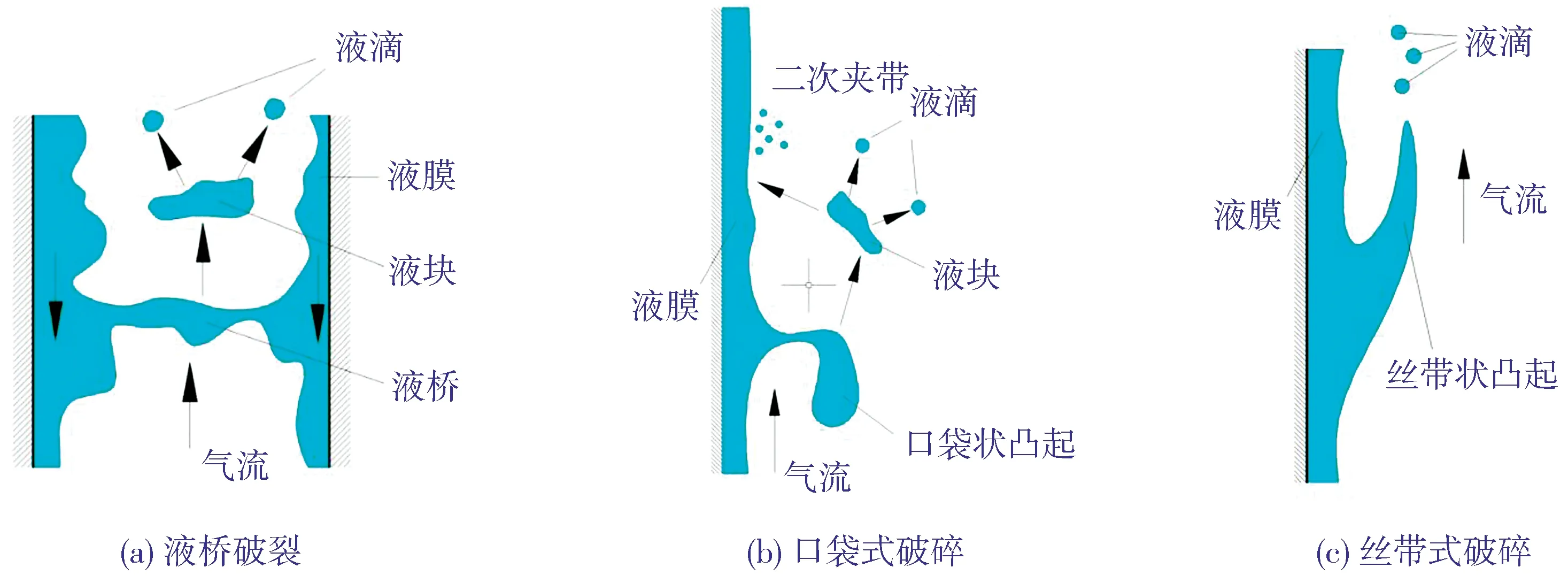
图4 搅拌流内常见液滴夹带方式
3 计算模型改进
搅拌流液膜初始流量可以表达为:
Gfo=G(1-xc)(1-Eoc)
(3)
式中:xc和Eoc分别为搅拌流起始点的干度和搅拌流起始点液滴夹带份额。由于在搅拌流起始点处的液滴夹带份额非常大,故本文假设搅拌流起始点液滴夹带份额为0.9,使之具有实际物理意义。
3.1 流型转变界限
计算过程包含2个流型转变界限,即弹状流-搅拌流的流型转变界限以及搅拌流-环状流的流型转变界限。
3.1.1 弹状流-搅拌流流型转变
Taylor气泡周围的下降液膜在向上运动的气流作用下失稳,即下降液膜出现液泛情况,被认为是由弹状流到搅拌流的转变。转变条件可以描述为【10】:
(4)
若
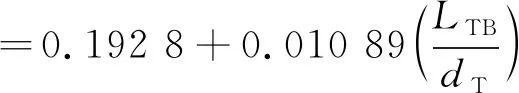
若
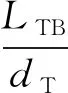
(5)
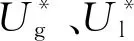
Taylor气泡长度LTB可以根据液弹单元内的液相质量守恒获得【11】:
usl=uSL(1-αs)(1-ζ)-usfζ
(6)
(7)
式中:uSL、αs、usf、Ls和ζ分别为液弹内液相流速(uSL=usg+usl,其中usg和usl分别为表观气速和表观液速)、液弹含气率、液膜表观速度、液塞长度(Ls=12dT)和无量纲系数。
McQuilian和Whalley【12】提出了弹状流内Taylor气泡表观速度usb及液膜表观速度usf的计算公式,如式(8)和式(9)所示。
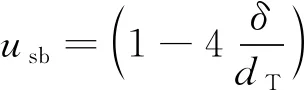
(8)
usf=usb-(usg+usl)
(9)
式中:g、ρl、ρg和δ分别是重力加速度、液体密度、气体密度和 Taylor气泡周围的液膜厚度。
液膜厚度δ可采用Jayanti和Hewitt【10】推荐的计算公式迭代求解。
(10)
(11)
式中:Δρ和εb分别是气液密度差和无量纲系数。
因此,基于式(4)~式(11)可以分别获得气、液两相表观速度usg和液相流速usl,在各相密度已知的情况下,可求解出气、液两相的质量流量,进而获得弹状流到搅拌流流型转变点处的起始点干度xc。
3.1.2 搅拌流-环状流流型转变
通常认为,下降液膜停滞并反转向上流动的时刻即为搅拌流到环状流转变的时刻。流型转变的临界条件可以表示为【13】:
(12)
因此,环状流起始点干度xa可以表示为:
(13)
3.2 液滴夹带率、沉积率、蒸发率
由液膜流动模型计算表达式可知,液滴夹带率、沉积率和蒸发率的计算公式对液膜沿流动方向上的分布有着至关重要的影响。
3.2.1 液滴沉积率md
液滴沉积过程非常复杂,气相场内液滴在气流湍流脉动的作用下会重新沉积到液膜表面。目前,对于液滴沉积理论主要是在绝热系统内获得的,并且是建立在线性假设基础上的,认为液滴沉积率与质量传递系数kd和气芯中液滴质量浓度C有关【14】,即
md=kdC
(14)
液膜表面蒸发会使得液膜附近的气相场扰动增大,阻碍液滴沉积。Peng【15】对液膜干涸区内热通量对液滴沉积率的影响进行了理论分析,认为液滴沉积必须克服由于液膜蒸发产生的扰动,并提出了适用于非绝热系统内的质量传递系数计算经验关联式:
(15)
式中:Prg和Reg是气相普朗特数和气相雷诺数。
3.2.2 液滴夹带率me
在非绝热系统内,液滴的夹带率分别由气相场剪切造成的夹带mes与液膜内核态沸腾产生的气泡在气液界面破裂造成的夹带meb组成。由于目前缺乏对由剪切夹带和气泡破碎夹带之间非线性关系的研究,因此假设总的液滴夹带率为两者的线性相加,即
me=mes+meb
(16)
由气相场剪切造成的夹带率mes可以采用式(17)进行计算【16】。
mes=ζmeH
(17)
式中:meH是环状流内液滴夹带率。
(18)
式中:σ是表面张力系数。
(19)
式中:Gg、Gf和Gfc分别是气体质量流率、液膜质量流率和液膜临界质量流率。
(20)
式中:μg和μl分别是气体粘度和液体粘度。
对于由沸腾产生气泡在气液界面破裂造成的液滴夹带率,本文采用Milashenko 等【17】的经验关系式进行计算:
(21)
式中:Mf为液膜质量流量。
3.2.3 液膜蒸发率mv
搅拌流以及环状流液膜流动过程中,蒸发率取决于壁面热负荷和汽化潜热的大小,可以采用式(22)进行计算。
(22)
式中:q和hv分别是热通量和汽化潜热。
3.3 各区域长度计算
管道任意位置处的含气率可以表示为:
(23)
式中:x(z)和xin分别是管道任意位置处的质量含气率和入口干度。
因此,搅拌流与环状流区域长度可以分别通过流型转变点的质量含气率获得:
搅拌流区域长度
(24)
环状流区域长度
(25)
式中:Lc和La分别是搅拌流区域长度和环状流区域长度。
3.4 计算流程
对式(1)进行离散,计算控制体内液膜流量沿流动方向的变化,可以表示为:
(26)
式中:Δz和j分别是节点间距和沿流动方向的各离散点。设j=0为搅拌流起始点,当流量较低时,设置节点数为100,当流量较大时,设置节点数为1 000,并验证计算结果与节点数无关。计算过程中,首先假设热流密度q,然后通过式(4)确定搅拌流起始点,分别计算液滴夹带率、沉积率和蒸发率,并代入式(1)确定液膜流量沿流动方向的分布。调整q初值,直至管道出口处液膜流量为零或接近零时,认为达到临界热流密度。计算工况范围如表1所示。
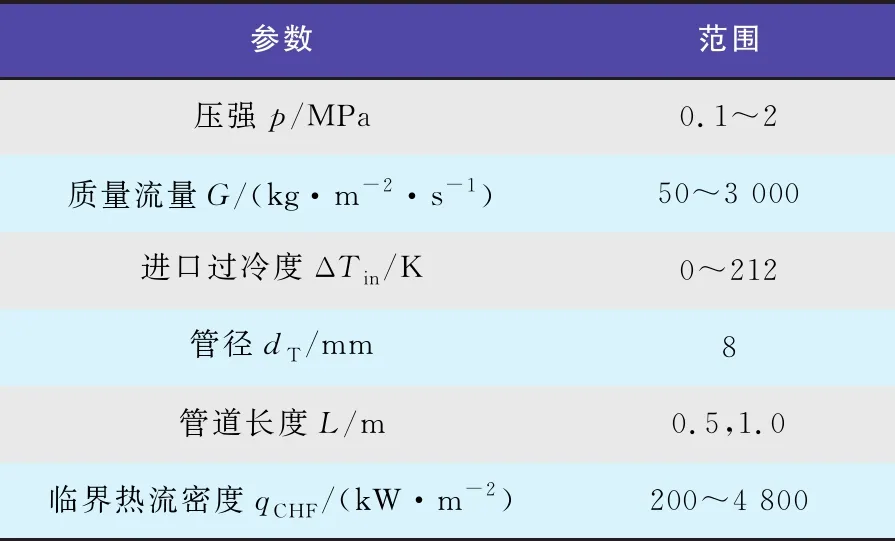
表1 计算工况
图5是CHF计算值q计算与实验值q实验对比,其中实验值由CHF LUT【18】获得。结果表明:改进后的模型计算结果绝大部分分布于±30%的误差带内,计算平均绝对值误差为14.79%。说明改进后模型不仅满足物理意义,且有效地改善了CHF计算结果受初始夹带份额影响的情况。
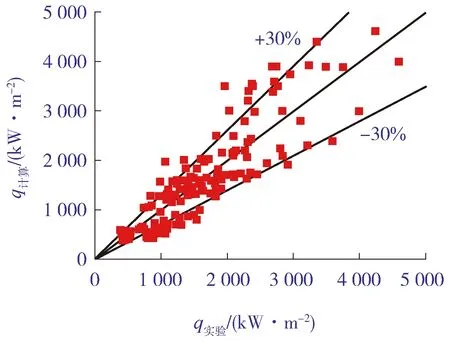
图5 CHF计算结果与实验结果对比
4 结论
1) 当质量流量较高时,环状流起始点初始夹带份额的选取对CHF计算精度、出口干度预测影响较大;
2) 搅拌流内具有较大动量的夹带液滴对下游环状流动有显著的影响;
3) 对原始环状流液膜流动模型进行了改进,考虑搅拌流区对CHF产生机理的影响,将液膜流动计算起始点提前至搅拌流起始点,更符合实际物理过程。
