高床载单组元肼发动机冷起动过程仿真研究

冀 鹏, 梁树强， 肖明杰， 雷凡培

(1.中国航天科技集团有限公司西安航天动力研究所液体火箭发动机重点实验室， 西安 710100； 2.航天推进技术研究院， 西安 710100； 3.中国船舶集团有限公司， 北京 100044)

床载荷是单组元发动机的重要设计参数[1]。床载荷越高，发动机推力室的结构尺寸越小，结构质量越轻。尤其在飞行器用于变轨的大推力单组元发动机提高床载时，该轻质化作用对整个飞行器就更为明显。然而不同于其他单组元发动机，单组元肼催化分解发动机可以实现室温下的自发起动，即冷起动，大大拓宽了其任务适用性，但在冷起动过程中常伴随着明显的压力峰，极大地影响着发动机的工作可靠性和飞行器的变轨稳定性[2]。因此，开展高床载单组元肼发动机的冷起动过程研究显得尤为重要。

单组元肼催化分解发动机冷起动过程的现象描述以及冷起动对推力器性能寿命的影响关系主要是由试验研究完成的。Kagawa等[3]采用中子放射线照相技术实现了催化床内液态肼流动状态的可视化，试验表明喷注压降并不影响肼的分解区域，而冷起动影响了在发动机催化床内肼的流动区域。刘昌国等[4]进行了单组元300 N发动机低温试验，发现温度差异、催化剂活性、低温下电磁阀响应对该发动机工作特性的影响。由于缺乏充分的过程认识和可靠的数值仿真手段，阿里安5号运载火箭[5]、美国航空航天局(National Aeronautics and Space Administration，NASA)空间飞行器[6-7]等所采用的单组元发动机也主要采用试验的手段来鉴定发动机的冷起动能力并评判其对发动机性能的影响。但依靠试验的方法难以对影响发动机起动过程的诸多因素及其组合开展全面系统的分析。

而在单组元催化分解发动机起动过程数值仿真方面，Schmitz等[8]将肼推力器的起动过程假设为气体充填和催化床温升换热两个子过程，并分别建立相应数学模型得到了发动机的起动过程数学模型，但该数学模型中采用修正因子来描述催化床入口处推进剂的分解，只能通过试验来获取修正因子限制了该模型的适用性。孙得川等[9]在此基础上进一步考虑相变过程通过计算流体力学的方法分析了硝酸羟胺基单组元发动机的起动过程，发现考虑相变过程后计算值与试验值吻合更好，但零维模型的计算结果仍令人满意。

上述学者通过试验和数值仿真的方法都将重点放在了起动边界温度和推力室内部复杂物理化学过程的研究上，而液体火箭发动机的起动过程是一个能量高密度释放和工况复杂变化的耦合过程[10]，起动控制对发动机起动过程也极具影响[11]。但目前尚未见从发动机系统的角度对单组元冷起动过程开展研究。为此，从减小起动瞬时流量的角度出发，建立反映冷起动延迟与分解过程平均效应的发动机冷起动过程数学模型，对某型高床载的单组元肼发动机冷起动过程开展仿真计算，分析系统结构对冷起动过程的影响规律，旨在为单组元肼催化分解发动机抑制冷起动压力峰提供理论参考与支持。

1 数学模型

单组元姿控动力系统是由气路增压系统、液路推进剂供应系统以及推力装置组成。对于恒压挤压的单组元姿控动力系统，贮箱增压压力基本保持不变，贮箱内液注静压和惯性压力的影响相对较小，忽略流体流出贮箱进入管路的损失[12]，假设贮箱内气体压力恒定，因此建立液路推进剂供应系统相关组件以及推力装置的动力学模型。

1.1 管路模型

在建立液体管路模型时不考虑管路的变形，认为管道为刚性的；管路内液体是一维的，管道横截面上的速度分布是均匀的。采用分段集中参数的管路模型。

对于特定的一段长度L、直径d、截面积A、体积V和粗糙度h的管路，考虑惯性、黏性时管路方程为

(1)

式(1)中：j为管路的惯性系数；qm为管路内流量；p1、p2分别为管路的入口压力与出口压力；ρp为管内液体密度；t为时间；ξ为总的流阻系数，由管路的沿程损失和局部损失组成[13]。

同时考虑液体的压缩性方程：

(2)

式(2)中：p为分段管路等效容积的压力；qm1、qm2为管路等效容积出入口流量；z=V/a2为管路的流容系数，表征管路流体的压缩性，其中a为液体推进剂的声速。

1.2 电磁阀模型

对于系统仿真中所关注的电磁阀响应时间和阀门开度建立相应的数学模型为[14]

(3)

式(3)中:qval为通过阀门流量；Aval为阀门流通截面积；pval、pv分别为阀门入口压力与出口压力；Γ为电磁阀开度与流量系数的乘积(即Γ=τCv，其中Cv为阀门的流量系数)，它主要由实验结果来确定。但当缺乏实验数据时，通常采用如下方法来确定。

当阀门打开时，有

(4)

当阀门关闭时，有

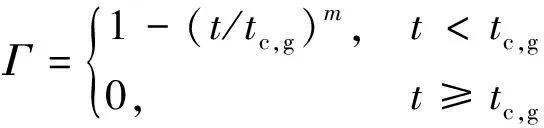
(5)

式中：tc,k和tc,g分别为电磁阀开启与关闭的响应时间；m为试验曲线拟合指数，主要由Γ-t曲线形状而定，一般情况下m为1～3。

1.3 催化床模型

采用反映平均效应的零维催化床模型。在建立催化床模型时做如下假设：分解产物为理想气体；不考虑气体的不均匀性和波动过程。

1.3.1 冷起动延迟模型

在单组元发动机冷起动时，由于初始温度较低、催化剂上微孔直径较小(微米量级)，液态推进剂会渗透到催化剂颗粒微孔内部进行分解。催化剂微孔内部的气液分界面会随着分解逐步外移直至分解气体溢出微孔，在整个催化床内建压。基于上述冷起动过程分析，对催化剂颗粒内部进行建模，计算气液分界面在颗粒微孔内部压力的作用下逐渐推移到微孔外的动态过程，得到单组元发动机冷起动延迟时间为[15]

(6)

式(6)中：M为气体产物的平均摩尔质量；a0为催化剂颗粒直径；Pm=2σcosθ/R为毛细压力，其中，σ为液态推进剂表面张力，R为大孔的特征半径，θ为接触角；Ru为气体常数；T为初始温度；D*P*为气相推进剂的扩散能力，D*P*=4.487×10-5T1.823；(ρA)vp为推进剂饱和蒸汽密度，(ρA)vp=2.45×108exp(-5 175/T)/T；ks=1010exp(-1 389/T)为推进剂的分解反应速率常数。

1.3.2 催化床建压过程模型

考虑到催化床内复杂的物理化学过程，引入燃烧时滞模型，假设推进剂在一定转化时间之后分解为燃气(此时间包括了推进剂蒸发、流动、分解时间的总和)。假设在该转化时间内推进剂的转化速率均匀，并且分解后的气体在任何瞬时也是均匀分布的，即氨的解离过程也近似认为与DT-3的分解过程同时进行。则液体推进剂及气体分解产物在催化床中的质量变化分别为[16-17]

(7)

(8)

催化床内压力由气体状态方程可得

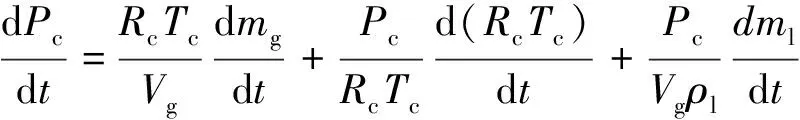
(9)

式(9)中：Pc为催化床平均压力；Vg为催化床内气体体积；Rc为催化床内气体常数；Tc为催化床内温度。

由于催化床内装载着紧密的催化剂，因此推进剂通过催化床时需要克服阻力称为床流阻，床流阻是催化床设计中的主要参数之一，采用文献[17]中的试验拟合公式计算。

2 仿真模型的建立及验证

以典型组件的数学模型为基础，根据模块化的建模思想，在MWorks软件平台上编制开发各典型组件的仿真模块。根据某次单台发动机地面试验的试车状态，对图1所示单台发动机地面试验系统搭建了相应的仿真模型。

考虑到所建立的数学模型是一组常微分代数方程组，在数值计算方法上选用四阶Range-Kutta方法进行求解模型，在初始参数赋值后，对该地面试验系统的冷起动过程进行了仿真计算。

考虑到试验系统中电磁流量计的测量频率较低，在较短的起动过程中无法准确测量系统的瞬时流量，因此主要对发动机室压Pc、阀前压力Pv的试验测量值与仿真值进行比较，验证仿真模型的准确性，计算结果和试验测量的对比如图2所示。对所有状态参数以设计值为参考都进行无量纲化，时间则以起动加速性要求为参考。

P为测量压力；Q为测量流量图1 发动机地面试验系统示意图Fig.1 engine ground test system schematic

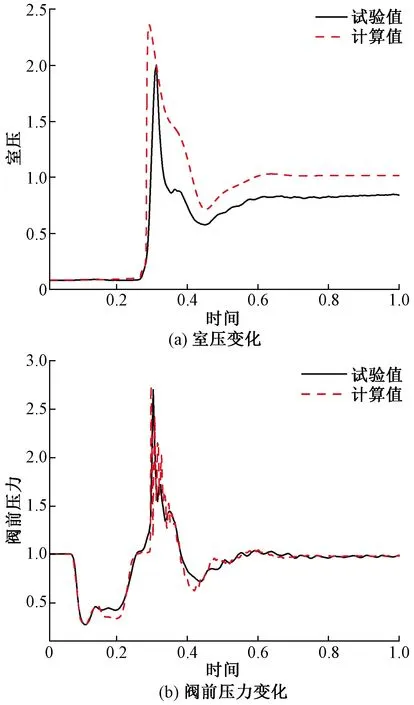
图2 发动机冷起动过程仿真结果与试验结果对比Fig.2 Simulation results compare with ground test results of engine cold starting process

从图2可以看出，发动机阀前压力的计算值与实测值吻合较好，而发动机室压的计算值与实测值之间有着一定的误差，稳态室压计算值较试验值偏高，引起这一误差的主要原因是试验测量压力值为喷管入口处的压力，而计算得到的压力是整个催化床内平均压力值；其次发动机冷起动时催化床初温较低随着反应进行分解效率随时间逐渐升高，而仿真中没有考虑分解效率的变化，将分解效率设为恒定的稳态分解效率，这两方面因素导致计算的稳态室压较高。计算的建压曲线相比试验建压曲线更为陡峭，则是因为催化床模型采用了反映平均效应的推进剂分解过程，假设在延迟时间内所积存的推进剂在同一时间发生分解，而实际中推进剂是由先进入的部分催化剂分解建压然后引起所积存推进剂发生链式分解，这导致计算建压过程快于试验测量的建压过程。

3 结果及分析

3.1 贮箱压力

对于挤压式发动机系统而言，贮箱压力直接决定着起动过程中推力装置的入口压力，对起动过程中进入管路及推力装置的瞬时流量有着至关重要的作用。对贮箱压力从设计值逐步增大进行了仿真计算，图3给出了在不同贮箱压力情况下发动机的冷起动过程曲线。

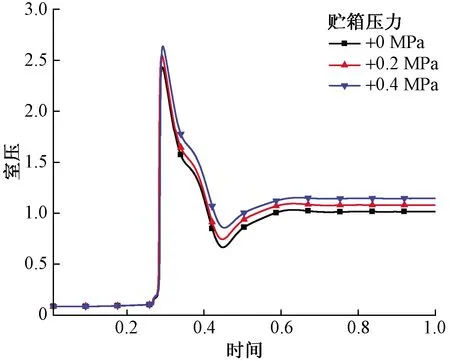
图3 贮箱压力对发动机冷起动过程的影响Fig.3 Influence of tank pressure on cold starting process of engine

贮箱压力越高，在起动过程推力室未建压前的推进剂流路中瞬时压差就越大，推进剂起动瞬时流量越大，在推力装置电磁阀打开后充填毛细管以及集液腔的速度就越快，在相同的冷起动时滞内催化床中积存推进剂就越多，提供给爆式分解的初始能量就越大，从而导致发动机冷起动时压力峰较高。

从图3可以看出，发动机冷起动压力峰随贮箱压力的升高略有增大；同时，贮箱压力的提高也引起了发动机在稳态工作时压力的升高，这是由于贮箱压力升高后系统压降提高，进入催化床内推进剂流量增大而导致了发动机稳态室压的提高。进一步得到贮箱压力变化与压力峰变化和稳态室压变化之间的关系，如图4所示。

图4 贮箱压力变化对冷起动压力峰及室压的影响Fig.4 Influence of variable tank pressure on pressure spike and chamber pressure of cold starting

从图4可以看出，对该型单机系统在所计算的贮箱压力变化范围内，压力峰变化和稳态室压变化与贮箱压力变化呈线性关系，冷起动压力峰的增大值约是贮箱压力提高值的62%，所造成稳态室压的增大值约是贮箱压力提高值的33%。稳态室压的增大幅度约为冷起动压力峰增大幅度的1/2。这是由于冷起动时推力室未建压，而稳态工作下推力室室压是随贮箱压力增大而增大的，因而在相同贮箱压力变化下，冷起动过程系统压降增大值大于稳态工作的系统压降增大值，冷起动过程流量相对变化也就大于稳态工作的流量变化。同时，在稳态流量较大的情况下，床流阻也会相应增大，故稳态室压随入口压力的变化幅值较小。

3.2 系统流阻

单台推力室的动力系统组件较少，在发动机系统参数发生变化时都会改变相应组件的流阻特性进而影响发动机的冷起动过程。因此，对不同毛细管长度、毛细管直径、电磁阀压降以及限流圈直径等典型组件的结构参数进行了仿真计算。

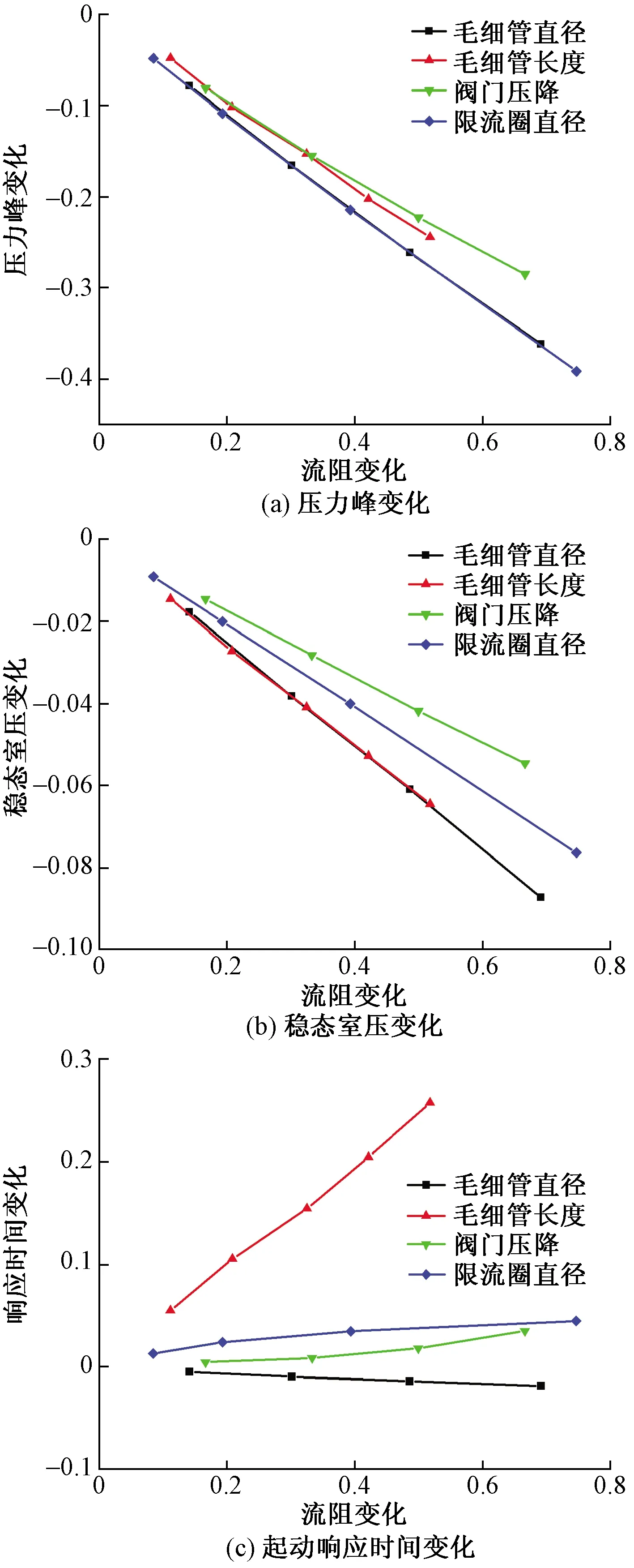
图5 不同结构参数对发动机冷起动特性的影响Fig.5 Influence of variable structure parameters on characteristic parameters of cold starting

图5给出了各个因素引起系统流阻增大的情况下，发动机冷起动特性参数的变化，如响应时间、压力峰和稳态室压。可以看出，毛细管长度的增加显著增大了发动机的起动响应时间并减小了发动机的稳态室压；毛细管通径、电磁阀压降以及限流圈喉径的变化对响应时间的影响较小；毛细管通径和限流圈喉径对起动压力峰值的抑制作用相当，但是毛细管通径所引起流阻变化对发动机稳态室压减小的作用更强，不利于系统稳态参数调节；而电磁阀压降所对稳态室压减小作用较小，相应的抑制压力峰作用也相对较差。因此，增大毛细管长度、电磁阀压降，减小毛细管直径、限流圈直径都可以在不同程度上抑制发动机的冷起动压力峰，但同时也影响了发动机的起动加速性和稳态工作性能。因此需要进一步对上述因素进行对比，综合考量3种结构参数对压力峰的影响。

结合工程应用中需要尽量保证稳态室压不变化，比较在保证稳态室压不发生改变的情况下4种增大流阻方式抑制压力峰的能力。考虑到3.1节贮箱压力和稳态室压成线性关系，因此通过提高贮箱压力以保证稳态室压恒定的情况下对上述4种结构参数变化进行仿真计算，对比不同结构参数引起相同流阻情况下冷起动压力峰变化的结果如图6所示。

图6 相同流阻变化下结构参数对冷起动压力峰的影响Fig.6 Influence of variable structure parameters on pressure spike of cold starting

从图6可以看出，限流圈喉径所表示的曲线斜率最大，这意味着在引起系统流阻相同改变的前提下，限流圈减小压力峰的作用最强，而毛细管长度增长的抑制作用最弱。因此，从保证起动加速性与稳态室压恒定的要求出发，调节系统结构参数中设置合理的限流圈对抑制冷起动压力峰的作用最强，同时综合研制周期与系统复杂性采取调节限流圈参数的措施也较为合理。

4 结论

(1)采用所建立的计算模型和计算方法，可以对单组元肼催化分解发动机冷起动过程进行数值仿真，得到的冷起动室压和阀前压力与试验结果吻合较好。

(2)贮箱压力对发动机的冷起动响应时间影响较小，贮箱压力升高时，冷起动压力峰和稳态室压都随之增加，冷起动压力峰增大幅值约为稳态室压增大幅度的2倍。

(3)增大毛细管长度会显著降低发动机的冷起动加速性，且对冷起动压力峰的抑制作用较小。

(4)对比了3种结构参数变化对冷起动过程的影响规律，发现从减小冷起动过程瞬时流量角度出发，综合控制限流圈内径是最为合理有效的抑制冷起动压力峰的措施。