预制装配式架桥机的起重小车复合滑模同步控制

韩林山， 刘 耀， 迟 明， 唐明昊

(华北水利水电大学机械学院， 郑州 450045)

随着中国经济的飞速发展，城市高架路的建设迫在眉睫，预制装配式架桥机[1]的设计是为了解决传统架桥机存在的架设周期长，占地面积大等问题。然而，现有的架设墩柱方法依然是采取“一步一停”的方式，严重影响了架设的精度和效率。目前，中外主要通过改进架桥机结构来提高架设速度，还未有学者考虑闭环控制系统对提高架设速度与精度的影响。而架桥机墩柱的架设需要后起重小车走行电机与升降电机的同步协调配合，对于同步协调问题，现已有很多研究，包括耦合控制[2-3]和非耦合控制[4-5]两大类，其中耦合控制中的交叉耦合控制在双轴系统中的同步控制精度较高，适用于所研究的系统。但是交叉耦合控制策略在一轴受到扰动后，另一轴也会失稳，因此必须搭配新的控制策略来提高其稳定性。许多学者将同步控制与跟踪控制相结合，提出了粒子群优化比例积分微分(proportion integral differential，PID)控制[6]、基于TSK型递归模糊神经网络(TSK-type recurrent fuzzy neural network，TSKRFNN)控制[7]、动态网络自适应控制[8]、鲁棒控制[9]等，都取得了不错的控制效果。滑模控制由于具备算法简单、抗干扰能力强以对及建模参数变化不敏感等特点受到了广泛的重视，并应用在很多领域。然而滑模控制需要较大的切换增益来增强其鲁棒性，随之而来的是抖振的产生，文献[10]使用饱和函数代替传统的切换面，并与模糊控制相结合来解决了系统参数不确定性问题，但同时会削弱系统的抗摄动性。文献[11]采用变边界层技术，折中了误差与抖振的问题，并使用参数自整定的方法来消除扰动。

众所周知，滑模面的品质对趋近速度的影响较大。文献[12]将双环积分项加入滑模面的设计中，使控制系统响应更快、无超调、鲁棒性更强，但积分项的引入存在控制输入变大以及收敛速度变慢的问题。文献[13]引入时变参数从而改变滑模面的斜率，使系统始在滑动阶段，进而提高了系统的鲁棒性。文献[14]提出了将自适反推互补的滑模控制策略与质量辨识观测器结合来抑制扰动，取得了较好的全局控制效果，但设计的控制器较为复杂，在复杂环境下的应用难度较大。

为此，首次将闭环控制系统应用在架桥机的起重小车上，通过分析架桥机起重小车实际架设墩柱过程，计算出走行电机与起升电机同步运动角位移关系式；然后建立起重小车起升与走行机构的动力学模型，通过上述文献的比较与启发，基于交叉耦合控制策略，提出了一种新的时变参数滑模面；为了抑制控制器的抖振，设计新的变增益滑模趋近律；由于起重小车负载大，扰动大，为提高起重小车在各种工况下的适应性与抗扰动性，设计一种新的时变扰动滑模观测器，以便有效估计并补偿扰动；最后对本文方法进行稳定性证明并使用数值仿真验证其有效性。

1 问题描述

1.1 起重小车运动过程分析

起重小车架设墩柱如图1所示，前后起重小车首先同步走行到架设区域，也就是图中墩柱水平状态，此时为初始位置。后起重小车在靠近前起重小车的同时需要起升电机降下吊具，因此，后起重小车的起升机构与走行机构需要符合一定的同步运动关系，才能保证架桥机在墩柱架设过程中的稳定性。起重小车的走行与吊具的升降都是由电机来完成，起升电机输出转矩通过轴与减速器传递给卷筒从而控制吊具升降，走行电机同样也是将转矩输出到车轮从而控制起重小车走行。

图1 架桥机起重小车架设墩柱简图Fig.1 Schematic diagram of erecting pier column by bridge erecting machine lifting trolley

1.2 同步运动关系

两电机的运动比例关系分析如图2所示。两电机角位置关系可表示为

L为两吊耳间距离；y1为起重小车走行距离，y1=θ1r1； y2为吊具下降距离，y2=θ2r2图2 架桥机起重小车架设墩柱模型Fig.2 Model of pier column erected by crane trolley of bridge erecting machine

(1)

1.3 后起重小车动力学模型

后起重小车运行机构模型如图3所示，根据其运动的物理特性，并且考虑电机的非线性特性、干扰以及所施加的负载，起重小车系统的动力学方程为

G为吊具与重物的总重力图3 后起重小车运行系统模型Fig.3 Model of rear crane trolley running system

ui(t)-τi(t)

(2)

在电机模型的参数变化、摩擦力及各种扰动的存在下，式(2)控制器设计变得复杂，由于滑模控制的鲁棒性，改写动力学方程为

(3)

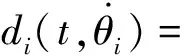
τi(t)]

(4)

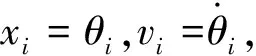
(5)

2 控制算法设计

2.1 滑模控制器设计

控制器设计的目标是在各种扰动存在的情况下系统能够实现对给定位置的准确跟踪和两电机在整个吊装过程中的同步。定义吊具与起重小车跟踪误差为

ei=xid-xi

(6)

定义同步误差为

(7)

定义两电机的交叉耦合误差为

(8)

式(8)中：αi>0为同步误差积分项系数。

取滑模面为

(9)

式(9)中：c1为时变滑模面参数；c2、c3、c4>0为滑模面系数；a>0为指数项参数。

c1(t)的表达式为

c1(t)=(φ1+φ2e-μt2)m

(10)

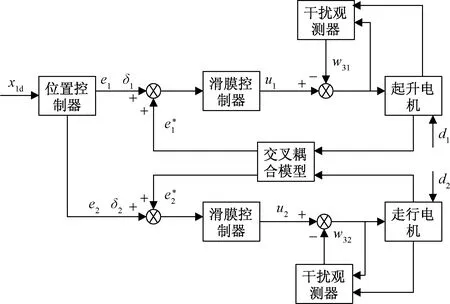
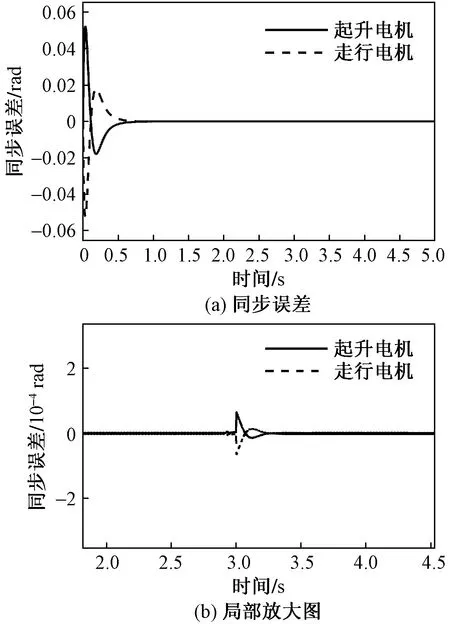
式(10)中：φ1、φ2>0为滑模面调整参数；m为指数项参数；μ>0为指数项参数；1

由于起升机构与走行机构的同步运动存在式(1)的位置比例关系，因此式(7)需要设计中间变量zi，从而保证同步误差选取的准确性。

c1(t)控制系统的收敛速度，但c1(t)的增大会使控制力也急剧增大，因此设计式(10)的时变参数，使系统在初始时刻有较大的值，随着时间的变化会逐渐减小。c4的选取与初始时刻有关，取值尽量使系统在初始时刻位于滑模面附近，这样可以提高控制器的鲁棒性。

为了减弱控制器的抖振现象，设计趋近律为

(11)

q(s)=k(1-e-δ|s|)

(12)

式(12)中：k、δ>0为调整参数。

由式(12)可知，当系统误差远离滑模面，即|s|增大时，q(s)趋近于k，当系统误差接近滑模面时，q(s)将逐渐趋向于零，从而使设计的控制器在不降低收敛速度的同时减弱抖振。

结合式(9)和式(11)可得控制力表达式为

(13)

证明建立Lyapunov函数：

(14)

对式(14)进行求导，得

(15)

将式(13)代入式(15)得

(16)

2.2 扰动状态观测器设计

为了使系统适应各种工况和扰动，设计了一种新的时变滑模扰动观测器，通过将实际系统与建立的扰动观测器进行误差比对，估计出扰动，进而反馈到实际系统中，实现误差的补偿。

改写式(5)，将di记作系统的状态变量，可得

(17)

(18)

(19)

式(19)中：βp、α>0为调整参数。

滑模扰动观测器的收敛速度与λp(t)有关，当参数λp(t)越大时，收敛越快，λp(t)的设计是为了避免当状态观测器的初值与原系统的初值不同时而产生的峰值现象，从而对观测器的收敛效果产生影响。

将式(17)与式(18)相减得到误差方程，可表示为

(20)

新的控制力可表示为

(21)

证明建立Lyapunov函数：

(22)

对式(22)进行求导，并将式(20)代入得

(23)

若要使上式小于零，需满足：

(24)

式(24)中：h为滑模安全因子，h>1 。

综上所述，在满足式(24)的参数选取原则下，式(18)所设计的扰动状态观测器将在有限时间收敛到零。所设计的控制器结构如图4所示。

w31、w32分别为起升电机和走行电机的干扰估计值图4 控制系统结构框图Fig.4 Block diagram of control system

3 数值仿真

利用MATLAB/Simulink仿真平台，对所需要设计的复合滑模控制器数学模型进行仿真,以此验证它们的控制特性。

起升电机各项参数为：J1=0.075 kg·m2，B1=0.02 N·ms/rad，L=8 000 mm，r1=300 mm，α1=30，φ1=3，φ2=3，μ=2，m=5/3，c2=1，c3=15，c4=-98，a=8，k1=0.8，k2=10，r=0.85，k=15，δ=0.8。

走行电机各项参数为：J2=0.007 kg·m2，B2=0.002 N·ms/rad，r2=200 mm，α2=30，φ1=3，φ2=3，μ=2，m=5/3，c2=1，c3=20，c4=-380，a=8，k1=0.8，k2=10，r=0.85，k=10，δ=0.8。

仿真1在无扰动的情况下，验证控制器收敛速度，以及抑制抖振能力。起升电机目标位置为x1d=5 rad，扰动d=0，仿真时间为5 s，其结果如图5所示。

图5 无扰动时仿真结果Fig.5 Simulation results without disturbance

跟踪误差如图5(a)、图5(b)所示，所设计的控制器可以使吊具在0.8 s到达规定位置；电机控制力如图5(c)、图5(d)所示，抖振得到了很好的抑制；从图5(e)可以看出，两电机的同步误差极小(0.06 rad)，并且误差的收敛速度也很快(0.8 s)。

仿真2在仿真1的基础上，施加常值扰动d=1 N·m，并在3 s时刻加入突变扰动d=2 N·m，所得结果如图6所示。

图6 常值扰动仿真结果Fig.6 Simulation results of constant disturbance

结果显示，在常值扰动下，图6(a)在3 s时几乎看不出突变扰动，图6(b)是在3 s时的局部放大图，可以看出，系统的同步误差收敛速度几乎没有受到影响，在加入突变扰动时，对系统同步精度的影响极小(0.000 3 rad)，并且在很短的时间收敛。

仿真3在仿真1的基础上加入扰动干扰观测器，施加持续时变扰动d=2sint，控制器参数为：β1=15，β2=120，β3=300，α=10。

结果如图7所示，估计误差曲线与实际误差曲线几乎重合，表明观测器的估计精度较高，将观测器估计出的扰动及时反馈到滑模控制系统中，可以有效地补偿扰动，从而提升了系统的鲁棒性。

图7 时变扰动仿真结果Fig.7 Time varying disturbance simulation results

4 结论

根据160 t全预制装配式架桥机实际架设墩柱过程，分析了起升电机与走行电机同步运动角位移关系式，并结合交叉耦合控制策略，设计了在有一定比例关系的同步运动系统中的同步误差获取方法，避免了两电机在耦合过程中存在控制参数紊乱的问题。并设计了时变参数滑模面，提升了系统的鲁棒性。接着设计了变增益趋近律，结果显示系统的收敛速度较高，抖振抑制效果明显。然后为了提高系统在各工况下的适应能力，设计了一种扰动滑模观测器，结果显示，观测器的估计性能较高，稳定性较强。通过Lyapunov理论证明了上述方法可以在有限时间内收敛。最后通过数值仿真证明了整个系统具有较快的收敛速度与较高的精度和抗干扰能力，为架桥机提升架设速度与精度提供了一种可靠的方案。