淹没射流破碎含瓦斯煤效率主控因素敏感性分析
2021-11-23马雄伟王兆丰杨腾龙陈金生李艳飞
马雄伟,王兆丰,2,3,杨腾龙,陈金生,李艳飞,席 杰
(1.河南理工大学安全科学与工程学院,河南焦作 454000;2.煤炭安全生产与清洁高效利用省部共建协同创新中心,河南焦作 454000;3.煤矿灾害预防与抢险救灾教育部工程研究中心,河南焦作 454000;4.河南焦煤能源有限公司古汉山矿,河南焦作 454000)
水射流技术在水力冲孔[1]、水力割缝[2]、水力压裂[3]等水力化煤层增透措施中应用广泛,其原理是利用高压发生装置使水获得巨大能量后,通过喷嘴射出进而冲蚀破碎煤体,使煤体充分卸压[4]。水力化措施在应用中,经常会出现淹没射流条件,对射流破煤的效率具有削弱作用,这直接影响水力化措施的效果,为了提高煤矿井下水力化措施的效率,展开不同射流参数对破煤效率的影响研究。许多学者对淹没射流进行了深入研究。在实验方面,向文英[5]等人利用淹没射流装置与分析了淹没磨料射流对岩石的冲蚀性能,发现在冲蚀质量上存在最优靶距直径比;侯亚康[6]利用磨料水射流系统,结合淹没实验装置,研究了靶距、压力、进给速度和磨料粒度等因素对花岗岩的冲蚀性能的影响;黄小波[7]等人利用淹没射流旋转割缝技术对煤体进行卸压增透,优化了喷嘴直径等参数;刘佳亮[8]、廖华林[9]、王宗龙[10]等人进行了淹没条件下水射流破岩试验,得出了破岩效率的影响因素;杨腾龙[11]、蒋斌[12]等人分析对比了淹没射流与非淹没射流的效率差异,为现场工作提供了参考。在数值模拟方面,陈欣欣[13]研究了冲击角度对淹没冲击射流流场的影响;李世杰[14]建立了射流破土数值模型,反映了冲蚀坑的演化规律;司鹄[15]等人模拟了不同冲击速度下应力波在岩石中的传播和衰减过程,得出应力波的传播速度与冲击速度的关系,文献[16]中仿真分析了泥土和射流之间的相互作用机理,模拟了坑形变化。综上所述,前人淹没射流破碎的对象多是岩石或土壤,而对淹没破碎含瓦斯煤体鲜有报道,且未对特定地质条件下影响淹没射流破煤效率主控因素进行分析,并且破煤过程极为短暂;为此,采用数值模拟的手段,建立淹没状态下水射流破碎含瓦斯煤流固耦合模型,通过模拟不同射流条件下破煤效率的差异,得出淹没射流破煤的主控因素,以期为煤矿水射流技术的高效应用提供指导。
1 数值模拟
采用Ansys/Ls-dyna 进行数值模拟,内嵌的ALE算法具有计算网格不再固定、可以相对于坐标系作任意运动的优点,因此采用ALE 算法计算分析淹没射流破碎含瓦斯煤的过程。淹没射流破煤效率影响因素主要包括水射流冲击条件、煤体自身特性、环境介质3 个方面[17],但现场应用中针对的是特定地质条件下的煤体,煤体自身特性和环境介质相差不大,因此只研究不同水射流冲击条件下的破煤过程。
1.1 模型建立及边界条件
淹没水射流冲击破碎煤体的过程是轴对称的,为了提高计算精度与速度,只需选取模型的1/4 进行模拟分析。网格划分采用自由网格及映射网格相结合的方法,对射流源、水域和瓦斯域采用自由网格法划分,对煤体采用映射网格法划分,淹没射流三维模型建立及网格划分如图1,模型参数设置见表1。模型底面设置ALL DOF 全约束限制底面移动;煤体、水域和瓦斯域各面为无反射边界,以模拟空间无限大的区域。
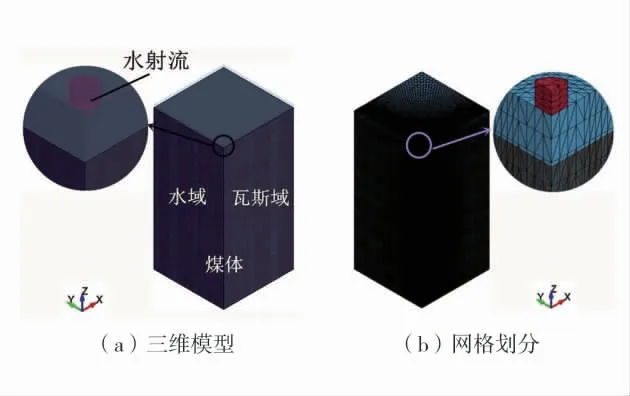
图1 淹没射流三维模型建立及网格划分Fig.1 Establishment of 3d model and mesh of submerged jet
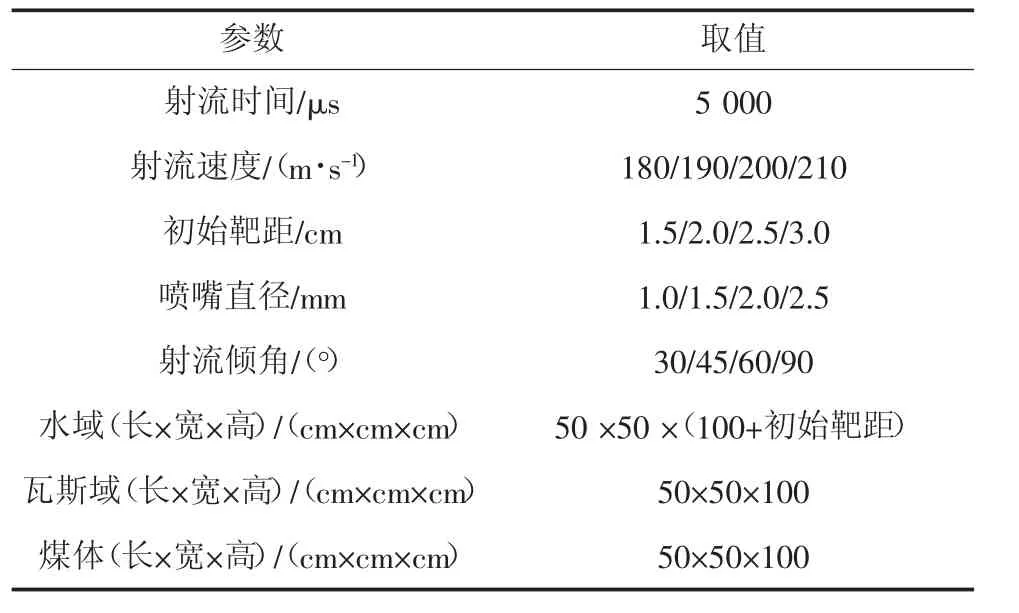
表1 模型参数设置Table 1 Model parameters setting
1.2 力学模型
连续性方程:
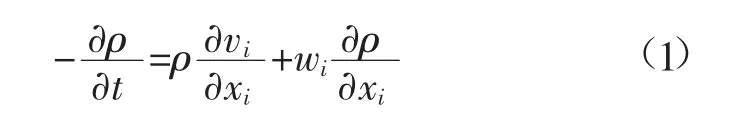
式中:ρ 为介质密度,kg/m3;t 为时间,s;vi为物质速度分量,m/s;xi为位移分量,m;wi为相对速度分量,m/s。
动量方程:
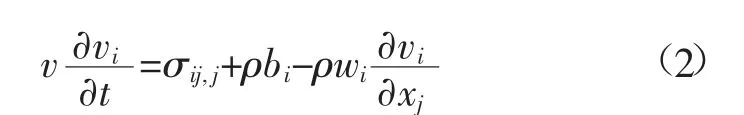
式中:v 为物质速度,m/s;σij,j为应力张量对坐标的偏导数,Pa/m;bi为体力,N;xj为位移分量,m。
能量方程:
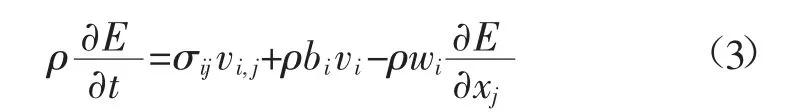
式中:E 为内能密度,J/m3;vj为物质速度分量,m/s;σij为应力张量;vi,j为物质速度对坐标的偏导数,s-1。
煤体本构方程:选取H-J-C 模型作为煤体的本构模型,其规范化等效应力描述如下:

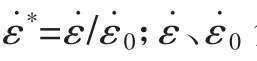
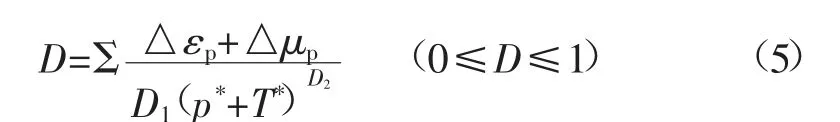
式中:△εp为等效塑性应变增量,无量纲;△μp为等效体积应变增量,无量纲;T*为最大拉伸静水压力,MPa;D1、D2为损伤常数。
瓦斯和水的本构方程:选取Gruneisen 状态方程表示,当材料受压时表示为:
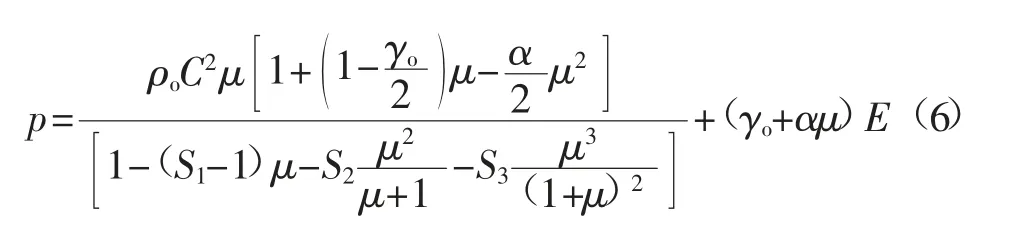
式中:ρo为初始密度,kg/m3;C 为冲击波速度μs与质点速度μp关系曲线的截距,m/s;μ 为黏性系数;S1、S2、S3为常数;γo为Gruneisen 系数;α 为泊松比[12];p 为材料受压时的压力,Pa。
冲击波速度μs与质点速度μp可通过式(7)进行相关联:
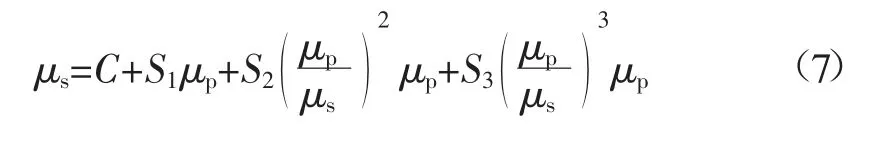
1.3 模型材料参数
1)煤体模型。建立4 MPa 围压的煤体模型,模型单元为持续应力固体单元,边界为无反射边界,恒定压力时间曲线的值为4 MPa,并调用此压力曲线后施加煤体各个面的节点上。煤体材料参数设置见表2。
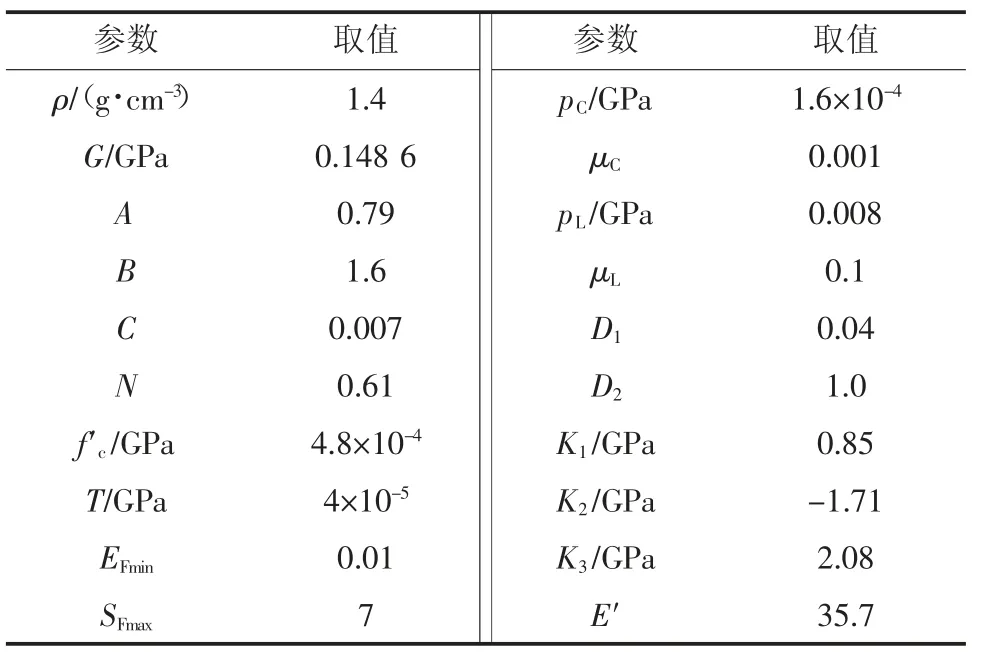
表2 煤体材料参数设置Table 2 Material parameters setting of coal
2)瓦斯域模型。瓦斯气体采用Mat_Null 材料模型,模型单元为ALE 多物质单元,边界为无反射边界,瓦斯气体施加压力为1 MPa。瓦斯域材料参数设置见表3。
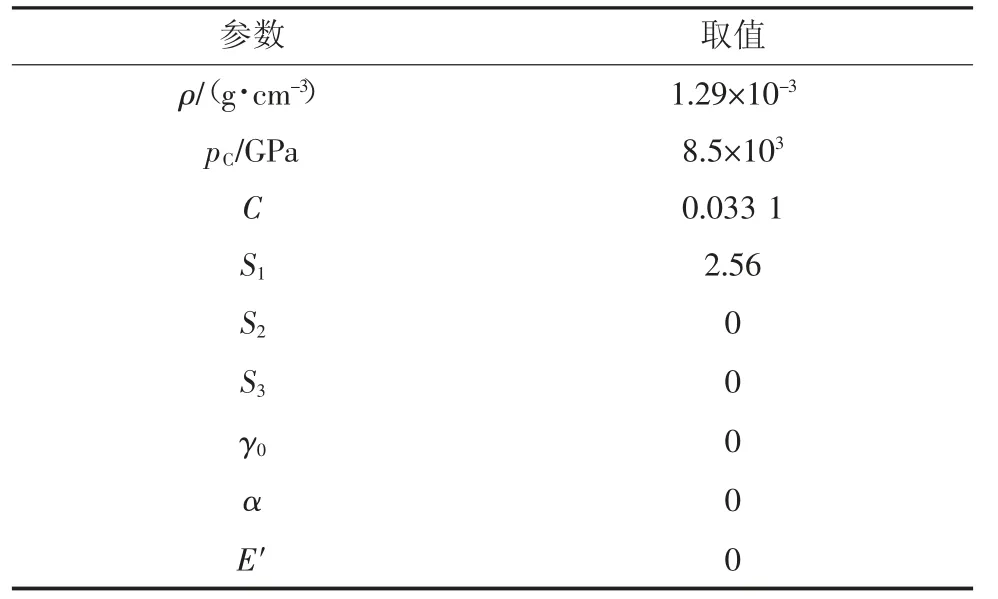
表3 瓦斯域材料参数设置Table 3 Material parameters setting of gas
3)水域及水射流模型。水域和水射流材料模型与模型单元同瓦斯域模型一样,为保证射流先与水域中的水体耦合,然后冲击煤体,因此设置罚函数耦合的同时允许侵入煤体单元。水射流和水域材料参数设置见表4。
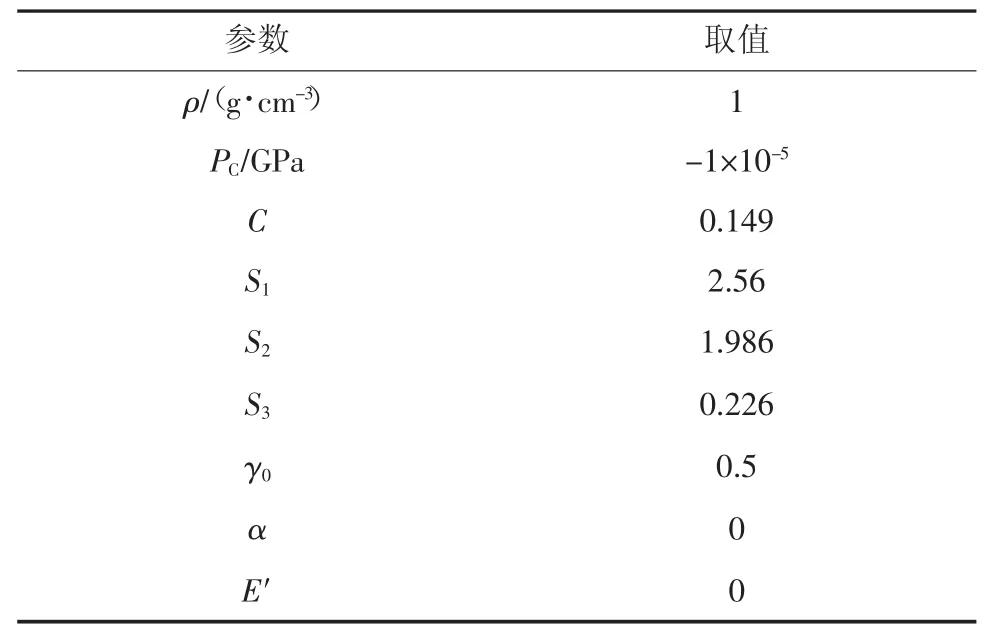
表4 水射流和水域材料参数设置Table 4 Material parameters setting of water jet and water area
2 结果分析
2.1 淹没射流破煤瞬时过程分析
将图1 中的淹没射流模型进行对称处理,并将破碎形成的坑体处放大,淹没射流破煤过坑形状图如图2。在破煤的初始阶段,射流破煤造成的坑体呈现出子弹形状,随着破煤的进行,破碎的坑体直径变大,深度也向下延伸。这是因为射流体由喷嘴高速喷出,其蕴含的大量动能与煤体发生交换,射流体不断冲击煤体,最终使破碎坑体直径变大,深度向下延伸。通过与试验对比,验证了数值模拟结果的可靠性。
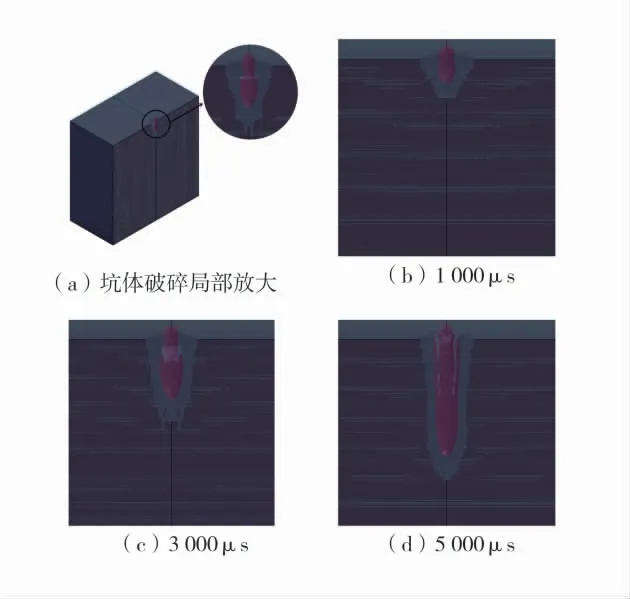
图2 淹没射流破煤成坑形状图Fig.2 Shape diagrams of coal pit formed by submerged jet
2.2 射流速度对破煤效率的影响
破煤深度、体积随射流速度的变化分别如图3、图4。
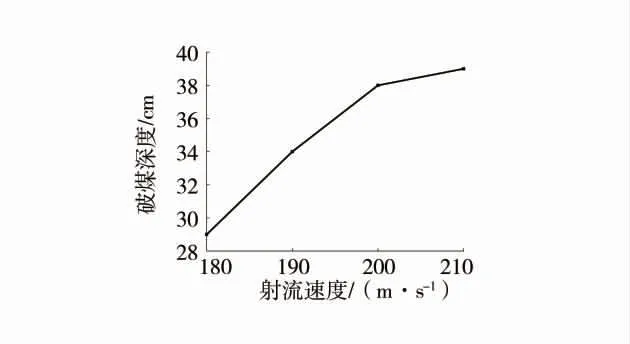
图3 破煤深度随射流速度的变化Fig.3 Variation of coal breaking depth with jet velocity
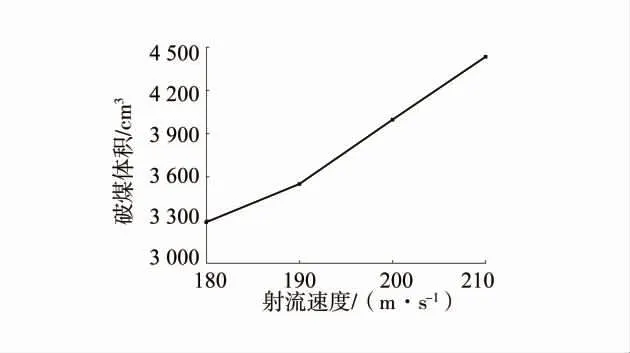
图4 破煤体积随射流速度的变化Fig.4 Variation of coal breaking volume with jet velocity
由图3、图4 可以看出,破煤深度及破煤体积与射流速度v 变化成正相关。当射流速度为180 m/s时破煤深度仅为29 cm,但210 m/s 时便可达到39 cm,增幅为34%,同理破煤体积增幅为33.9%。水射流速度的衰减是射流体与外界环境发生动量交换引起的,射流速度越大,动量就会越大,射流沿程衰减到破煤临界速度的距离变远,因而破煤效果越好。另外,相对于直径不变的喷嘴,射流速度的增大会直接导致流量随之越大,单位时间内作用于煤体的射流体的总量增加,因而会产生更大的坑体深度及坑体体积。
2.3 初始靶距对破煤效率的影响
破煤深度、体积随初始靶距的变化如图5、图6。
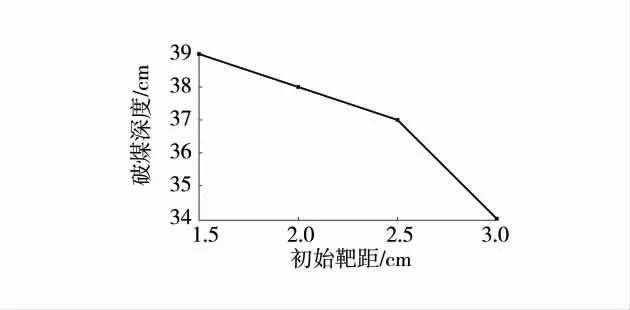
图5 破煤深度随初始靶距的变化Fig.5 Variation of coal breaking depth with initial target distance
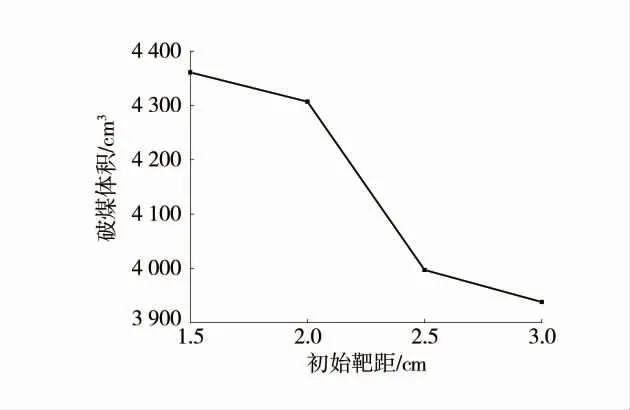
图6 破煤体积随初始靶距的变化Fig.6 Variation of coal breaking volume with initial target distance
由图5、图6 可以看出,破煤深度及破煤体积与初始靶距L 变化成负相关。这是因为靶距越大,射流体与水域交换时间越长,速度衰减幅度越大,因而破煤能力越弱。井下水力冲孔、水力割缝等水力化措施中,射流体初始靶距不会太大。当初始靶距为1.5 cm 时,破煤深度为39 cm;当初始靶距为3 cm 时破煤深度为34 cm,减幅仅为12.8%。同理,破煤体积衰减幅度仅为1%。不同初始靶距下的破煤深度及破煤体积并未显现出较大差异,这是因为破煤过程处于全程的淹没条件,较小的初始靶距相对于最终形成的较深的破碎坑体,对破煤效率的影响程度并未太大。
2.4 喷嘴直径对破煤效率的影响
破煤深度、体积随喷嘴直径的变化分别如图7、图8。
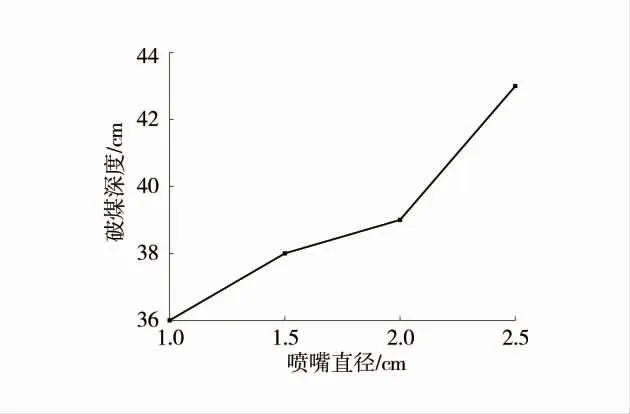
图7 破煤深度随喷嘴直径的变化Fig.7 Variation of coal breaking depth with nozzle diameter
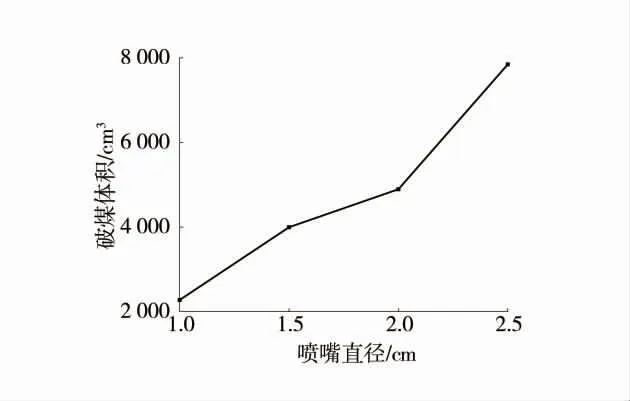
图8 破煤体积随喷嘴直径的变化Fig.8 Variation of coal breaking volume with nozzle diameter
由图7、图8 可以看出,破煤深度及破煤体积与喷嘴直径变化成正相关,射流速度不变的情况下,喷嘴直径越大,射流从喷嘴喷出时截面越大,流量就会越大,单位时间内作用于煤体的射流体便会越多,形成的破碎坑体体积就越大。当喷嘴直径从1 mm 增至2.5 mm 时,破煤体积增幅为263.6%,但破煤深度增幅仅为19.4%,由此可以看出,喷嘴直径对破煤效率的影响主要体现在破煤体积上。
2.5 射流倾角对破煤效率的影响
破煤深度随射流倾角的变化如图9,破煤体积随射流倾角的变化如图10。
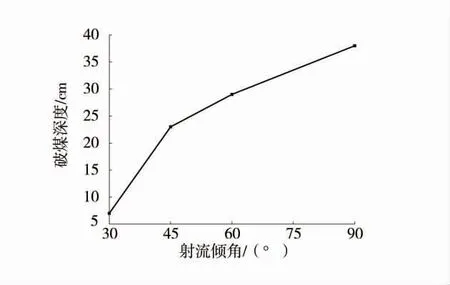
图9 破煤深度随射流倾角的变化Fig.9 Variation of coal breaking depth with jet angle
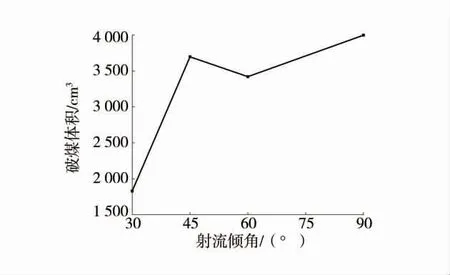
图10 破煤体积随射流倾角的变化Fig.10 Variation of coal breaking volume with jet angle
由图9、图10 可以看出,破煤段深度与射流倾角α 变化成正相关,当射流倾角为30°时,破煤深度仅为6 cm,90°时便可达到38 cm,增幅为533.3%,数据结果显示射流倾角对破煤效果的影响极为显著,煤体破碎坑体深度在射流与煤体相互垂直时达到最大值,因为当入射水流与煤体存在夹角时,射流速度可分解为垂直和平行于煤体表面2 个方向,射流倾角越大,垂直于煤体方向的冲击动量就越大,因而破碎坑体越深。破煤体积随射流倾角的增加呈现先上升后下降再上升的趋势,在90°达到最大值,因此从淹没射流破煤整体效率来看,射流倾角90°时最为适宜。
2.6 射流参数影响程度主次顺序分析
利用Ansys/Ls-dyna 数值模拟软件,按照正交试验方案对淹没射流破煤效率进行模拟计算,以破煤深度作为破煤效率的评价指标,对淹没射流破煤效率主控因素的极差进行求解,设置1 个空列作为试验误差以衡量试验的可靠性。采用极差分析法判断各因素对结果影响的主次顺序。极差分析见表5。
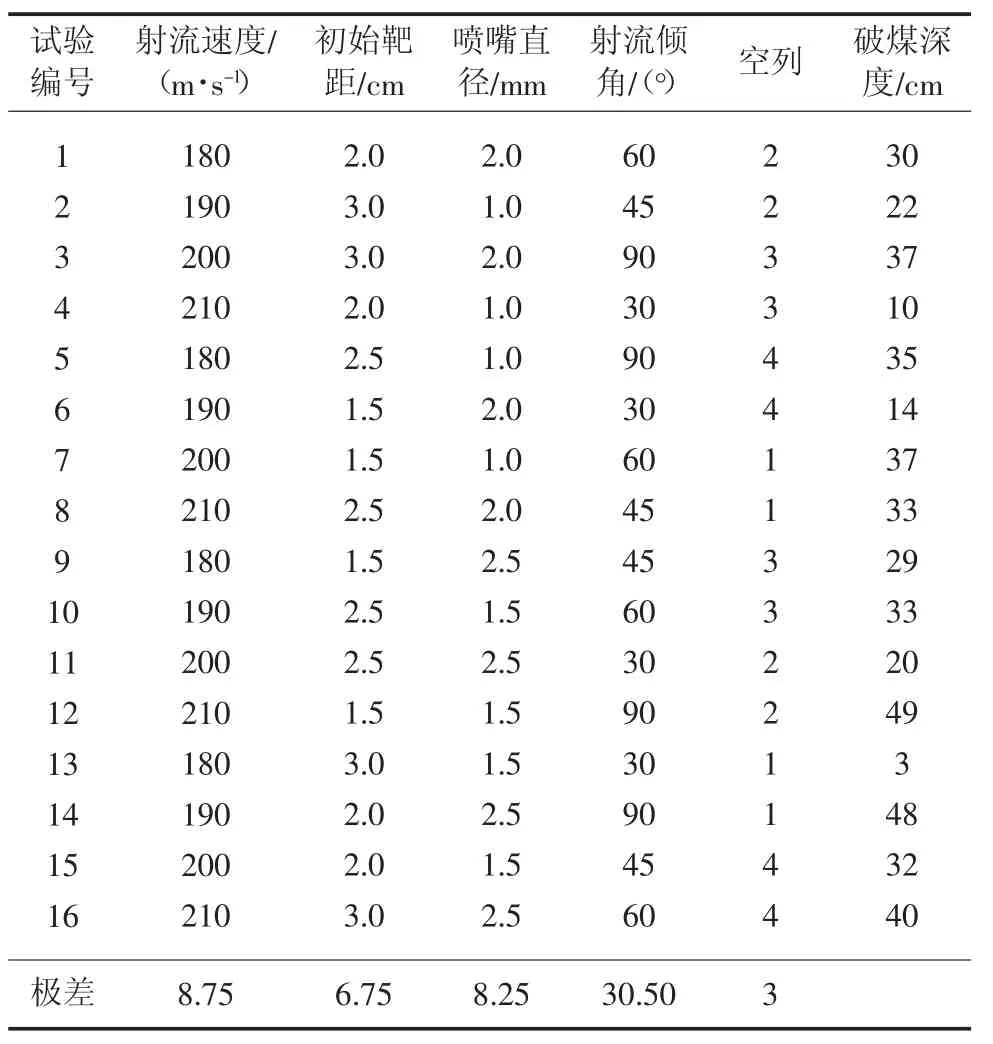
表5 极差分析Table 5 Range analysis
从极差分析结果可以看出,各个因素对淹没射流破煤效率的影响程度按大小依次为:射流倾角>射流速度>喷嘴直径>初始靶距。
3 结 论
1)淹没射流条件下,射流破煤过程初始阶段形成子弹状的破碎坑体,随着射流破煤的进行,射流体不断冲击煤体,其动能转移到煤体内部,致使破碎坑体直径变大,深度呈向下延伸。
2)淹没射流条件下,破煤深度及破煤体积与射流速度、喷嘴直径变化成正相关,与初始靶距变化成负相关,煤体破碎坑体深度在射流与煤体相互垂直时达到最大值,破碎坑体体积随射流倾角增加呈现先上升后下降再上升的趋势,在90°达到最大值。
3)运用极差分析法,得到不同射流参数对淹没射流破煤效率影响程度主次顺序依次为: 射流倾角、射流速度、喷嘴直径、初始靶距。因此,井下淹没环境下水射流技术应用过程中,要想取得较好的破煤效率,参数选择上应首先保证射流倾角,其次应关注射流速度,然后是喷嘴直径和初始靶距。
