“三角形的分类”教学实践与思考

陈雅 吴建亚

【摘 要】数学课堂要循着新教材的修改意图，理解教材的编排与要求，以更好地培养学生的数学思维。教师要时刻把培养学生整体思维、求异思维、创新思维等重要思维品质作为每一节课的教学目标，让学生在逐步发展数学思维的过程中，养成具有生长性的必备品格与关键能力，最终提升学生的数学核心素养。

【关键词】整体思维 求异思维 创新思维

“三角形的分类”是苏教版数学四年级下册的内容，旨在让学生通过观察、比较、归类等活动，经历给三角形分类的过程，认识并辨别锐角三角形、直角三角形和钝角三角形，了解各种三角形的特点。这节课可以说是一节“老”课，但修订教材对这一块内容有所调整，而很多一线教师却没有关注到教材的变化，还按着“老方子”教学，令人遗憾。如何循着新教材的修改意图，理解教材的编排与要求，将老课新上，从而更好地培养学生的数学思维呢？基于此，我们对这一课展开了研究、实践与思考。

数学课堂可以发展学生哪些思维，我们进行了如下思考。

一、对點状思维和整体思维的思考

【教学片段】

（1）复习角的分类

师：同学们来到农场做志愿者服务。为了庆祝农场成立，举办了一场灯光晚会。看，舞台上的灯光漂亮吗？

生：漂亮！

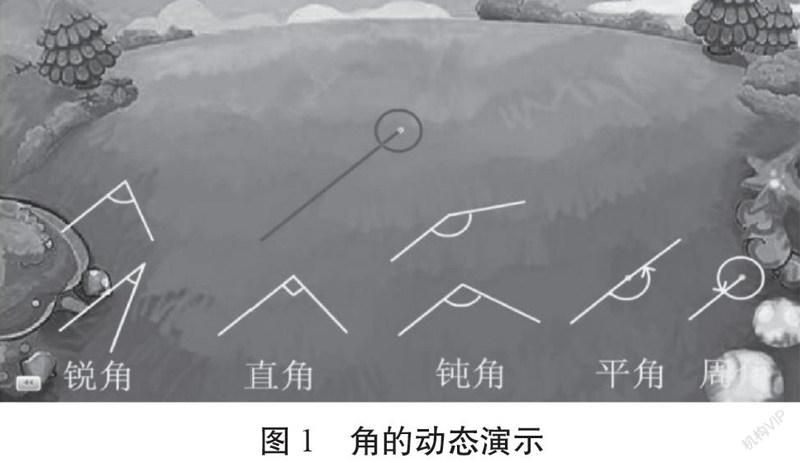
师：灯光里还有数学知识呢。瞧，如果把射灯看作一个端点，射出的光线看作一条射线，把这条射线绕着它的端点从一个位置旋转到另一个位置，就形成了一个（角）。这是一个什么角？（锐角）

师：那请同学们想象一下，如果继续旋转这条射线，还会形成什么角呢？我们一起来转一转、说一说。

师：什么角？（锐角）继续转。（直角）继续转。（钝角）继续转，现在（平角），旋转一圈（周角）。

师：根据角的度数，我们可以把角分成这样几类，见图1。

（2）引入三角形的分类

师：农场里还藏着许多三角形呢，我们一起来找一找、看一看。

（课件播放）

师：三角形和角一样还有很多，可以画多少个不同的三角形（无数个），那我们用省略号来表示无数个。

师：看了这么多三角形，你有什么想法？我们怎么来区分它们？要不，给每一个三角形都取个名字？（不可取）无数个三角形，取不完呀！那应该怎么办？

生：可以根据角给三角形分类。

师：这位同学觉得可以根据角的特征来给三角形分类。好，就听她的，那今天我们就从角的特征入手，对三角形进行分类。

师：为了便于研究，我们从这么多的三角形中选出5个，老师给它们标上序号、排排整齐。

【思考】

以农场射灯的情境表征角的动态定义，从而引入角的分类，接着引出三角形，再自然而然地引向三角形的分类需求，这样设计注重新旧知识之间的联系。将三角形放在平面图形中考察，而不单独割裂开来学习，体现数学思维的整体性。从农场实物中抽象出三角形，学生感受到三角形和角一样有无数多个，最终选5个三角形展开研究。这一过程培养了学生思维的整体性，因为个体的背后是一个整体，这5个是三角形世界中的代表。

抛出“大问题”，让学生小组合作讨论解决，我们发现，这样的课堂更精彩。学生对这些三角形按角的特征进行分类，首先依据的标准是三角形里有没有直角，在此基础上，部分学生再将经验迁移，思考三角形里有没有钝角、是否全是锐角，这些学生采取的是二分法。还有部分学生直接根据角的特征，采用了三分法。最终，班级学生一共得到四种分法，在下一环节，我们设计了将四类分法整理为同一类的教学环节，这一过程也体现了思维的整体性，因为整体思维是追求各种关系的一种整合。我们发现，改进后的教学设计，学生在推动着课堂生成的同时，自身也在逐步形成有意义的学习建构。“三角形的分类”一课，很多教师往往过分关注学生会不会对三角形按角的特征来分成三类，而忽视了更重要的向学生渗透数学中的分类思想，即“根据教学对象的共同性与差异性，把具有相同属性的归入一类，把具有不同属性的归入另一类”。减少教师的“铺路”，给学生一定的空间与时间对问题进行全局性思考，充分发挥学生的主观能动性，能更好地培养学生思维的整体性。

笔者认为，教师在教学“三角形的分类”一课时，应该培养学生的整体思维而不是点状思维，这也是为何修订教材时把表格删去的原因吧。

二、对求同思维和求异思维的思考

【教学片段】

师：三角形还有很多很多，数也数不尽。那根据角的特征，是不是只能分成这样的三类（锐角三角形、直角三角形和钝角三角形）呢？

生1：角还有平角和周角，三角形应该还有其他类别。

生2：我觉得所有的三角形只能分成这样的三类。

师：到底哪位同学的猜想是对的呢？

（1）钉子板操作验证。

（2）三角形内角和的推理验证。

（3）几何画板多样验证。

师：刚才同学们围出了很多三角形，也都只有这三类。是不是根据角的特征，三角形真的只能分成三类吗？其实啊，数学家也思考过这个问题，他们利用几何画板来研究，我们来看看。

师：通过刚才的演示，你有什么发现？

生：根据角的特征，三角形只能分成这三类。

师：你真会概括。现在，我们可以十分肯定地说——

师生齐：根据角的特征，三角形只能分成这三类。

【思考】

我们发现，这样的教学不仅藏着许多探究活动，而且还向学生渗透了不完全归纳推理等数学思想，给学生提供了思考的土壤，与原有设计中教师的直接告知形成了鲜明的对比。学生通过动手在钉子板上围一围——围不出第四种三角形、用三角形内角和的知识来推理——发现一个三角形最多只有一个直角或钝角、在几何画板上移一移——没有第四种三角形出现。最终，学生们十分肯定地说出：根据角的特征，三角形只能分成这三类。而这一切，源于教师对学生“求异思维”的保护，让学生猜一猜，充分尊重了学生的体会与感悟。

“求异探索是一种富有创造性的辨异思维”，当课堂上只有一种声音，大家都在“求同”时，敢于说出自己不同意见“可能还有其他类三角形”的学生，虽然不一定正确，但其勇气就值得教师肯定。原有的设计，只“求同”——让学生知道所有的三角形按角分类只有三种，从而快速完成本课的重难点;而改进设计后慢下来的教学则更关注“学生的个性心理差异，使他们能更深入细致且灵活变通地掌握知识”。苏教版修订教材时将“三角形的内角和”前置于“三角形的分类”，这样的编排凸显了知识发生、发展的逻辑顺序，为学生“求异”思维的培养提供了条件。

三、对常规性思维和创造性思维的思考

【教学片段】

练习：

（1）给出三角形两个锐角的度数，判断是什么三角形。

①30°，60°        （   ）三角形

②7□°，5□°      （   ）三角形

（2）露出三角形一个角，判断是什么三角形。你最想猜哪一个信封。

【思考】

第（1）题的题①，学生通过三角形内角和的知识进行计算后进行判断，符合学生的思维发展规律。教师小结时提到“这两个锐角之和是90°，它就是一个直角三角形”，为接下来的教学做铺垫。

当题②出示时，学生不约而同地发出“啊”的惊叹声，他们发现角度越来越小了，甚至影响他们通过计算来判断。面对这样的习题，学生们陷入了深深的思考中，有一部分学生用举例子带入数据来计算得出结论，但明显发现有些烦琐且容易出错;还有一部分学生则发现这两个锐角度数之和大于90°，那么第三个角度数肯定比90°小，所以肯定是锐角三角形，通过已知两个锐角度数之和与90°的关系推理出了结论。这样的教学尊重学生的个体差异，正视不同个体之间的思维差距，数据留白了，学生的思维却从低阶迈步进入了高阶。

在题②基础上，有的学生甚至说出如果已知两个锐角度数之和小于90°，那么这个三角形肯定是钝角三角形。从这个结论的得出，可见学生对所有情况都进行了分析，体现了思维的整体性和深刻性。计算与推理相結合的解题思路，必然会引起学生的头脑风暴，最终促进学生形成高阶思维。

第（2）题的“你最想猜哪一个信封”，极大激发了学生的解题兴趣。这一问不仅引导了学生去判断三角形的类型，更让学生得以思考自己的选择。具有不同数学思想的学生会做出不同的选择。选择从简单出发的学生注重由易向难，选择从高挑战性出发的学生则突显了其探究欲。教师应该尊重学生的个体差异。

数学课堂是学生发展思维的重要场所，而每一节课、每一个环节甚至每一句话都可以是载体，教师要时刻把培养学生整体思维、求异思维、创新思维等重要思维品质作为每一节课的教学目标，真正遵循学生的思维发展规律——由浅入深、从简到繁、从易到难来开展教学，让学生在逐步发展数学思维的过程中，养成具有生长性的必备品格与关键能力，最终提升学生的数学核心素养。