基于Cubic映射的灰狼优化算法及应用*
2021-11-22张孟健
张孟健,张 浩,陈 曦,杨 靖
(贵州大学电气工程学院,贵州 贵阳 550025)
1 引言
灰狼优化GWO(Grey Wolf Optimization)算法是澳大利亚学者Mirjalili等[1]在2014年提出的一种新的群体智能优化算法。GWO算法以灰狼的等级制度为特征,以求解连续变量的优化问题为背景,其思想是受灰狼群的捕食行为启发,进而模拟灰狼的群体狩猎等级制度并进行理论化研究。
标准GWO 算法也存在易陷入局部最优、后期收敛速度慢和求解精度不高等问题。GWO算法中,收敛因子a起到平衡算法全局和局部搜索能力的作用,但是,收敛因子a采用线性方式减小并不能很好地平衡算法的全局和局部搜索能力。因此,很多研究人员对GWO算法进行了一系列的优化改进。针对收敛因子a,魏政磊等[2]提出基于余弦函数和二次函数的非线性动态变化收敛因子更新方法;胡小平等[3]提出一种基于指数变化的参数调整策略,并运用在二维平面的无线传感器网络节点部署中;崔明朗等[4]通过添加“观察”策略以及对控制参数a的调整策略进行改进,提出了一种用于解决多目标问题的改进GWO算法。针对初始化策略的研究中,滕志军等[5]引入Tent映射来初始化种群,并将粒子群优化PSO(Particle Swarm Optimization)算法与GWO算法相结合构成新的混合算法;谈发明等[6]提出改进非线性收敛方式的GWO算法,从混沌初始化和非线性控制策略2个角度改进了GWO算法;王志华等[7]提出了基于混沌的GWO算法,并用于提高SVM(Support Vector Machine)分类器的分类精度;Ibrahim等[8]提出了一种基于差分进化和扰动算子的混沌对立的GWO算法;Saxena等[9]提出了一种基于β-混沌序列的自适应桥接机制来调节控制参数a,用于改进GWO算法,提高算法的全局和局部搜索能力;此外,莫艳红等[10]提出一种基于莱维飞行的GWO算法,一定程度上提高了算法寻优的精度,加快了收敛速度;Dhargupta等[11]提出一种基于反向学习的GWO算法来进行特征选取,增强了算法特征选取的性能。但是,上述改进策略还有可提升空间,因为目前许多智能算法均属于随机算法,采用了蒙特卡洛思想,不能完全保证对任何问题都能达到最优。
从上述2个角度对GWO算法的改进研究中,均在一定程度上提高了算法的搜索能力,但并不能解决算法在寻优过程中固有的不足。本文针对上述2个角度,提出了基于Cubic映射和反向学习策略的灰狼优化COGWO (Grey Wolf Optimization based on Cubic mapping and Opposition-based learning)算法,增强算法种群的多样性,从而提高其寻优能力和收敛速度。
2 标准灰狼优化算法
GWO算法模拟了狼群的社会等级制度和群体的狩猎行为[1],算法中每匹灰狼代表一个候选寻优解,将最优解设为α狼;次优解设为β狼;第3优解设为δ狼,剩余的解为ω狼。
灰狼群狩猎过程包括接近和包围猎物,其数学表达式[1]如式(1)和式(2)所示:
D=|C·XP(t)-X(t)|
(1)
X(t+1)=XP(t)-A·D
(2)
其中,D为个体与目标之间的距离;t为当前的迭代次数;C和A为系数向量;XP为目标的位置向量;X为单匹灰狼的位置向量。其中,A和C的计算公式如式(3)和式(4)所示:
A=2a·r1-a
(3)
C=2r2
(4)
其中,C为1×1向量C的值,A为1×1向量A的值,r1,r2为[0,1]的随机数;a为收敛因子,其值随迭代次数的增加从2线性递减至0,如式(5)所示:
a=2-2t/Tmax
(5)
其中,Tmax为最大的迭代次数,t=1,2,…,Tmax。
灰狼个体跟踪猎物位置的公式表述如式(6)所示:
(6)
其中,Dα,Dβ和Dδ分别表示α,β和δ与其他个体之间的距离;Xα,Xβ和Xδ分别表示α,β和δ当前的位置;C1,C2和C3为随机系数向量;X为单匹灰狼的当前位置向量。
在猎捕阶段中,剩余的ω狼个体向着α,β和δ狼的前进步长和方向如式(7)所示:
(7)
灰狼个体位置的更新公式如式(8)所示:
X(t+1)=(X1+X2+X3)/3
(8)
3 对GWO算法的改进
GWO算法虽然具有较好的寻优能力,但对于高维问题存在易陷入局部最优等问题。本文主要针对算法种群的初始化与收敛因子a2个方面,通过增强算法种群的多样性和动态选择收敛因子的值对GWO算法进行改进。
3.1 Cubic映射
标准的Cubic映射[12]函数可以表示为式(9)所示:
(9)
其中,b,c为混沌影响因子,不同的b,c值Cubic映射的范围也不同。一般在c∈(2.3,3)时,Cubic映射产生的序列为混沌状态。此外,当b=1时,xn∈(-2,2);当b=4时,xn∈(-1,1)。
文献[13]对常用的16种一维混沌映射的最大Lyapunov指数进行了计算分析,Cubic映射表达式如式(10)所示:
(10)
其中,xn∈(0,1);ρ为控制参数,Cubic映射的混沌性与参数ρ的取值有着很大的关系。由文献[13]可知,Cubic映射的混沌性与Logistic映射、Tent映射的最大Lyapunov指数相近,且优于Sine映射、Circle映射、Singer映射和Kent映射等一维映射。文献[14]提出了一种改进的Cubic映射,其最大Lyapunov指数为1.098 4,优于Logistic映射的Lyapunov指数0.693 0。
本文中,参数ρ的取值为(1.5,3),根据式(10)进行仿真,其结果如图1a所示。xn的初值为(0,1),取x0=0.3,ρ=2.595时,Cubic映射具有较好的混沌遍历性,仿真结果如图1b所示。
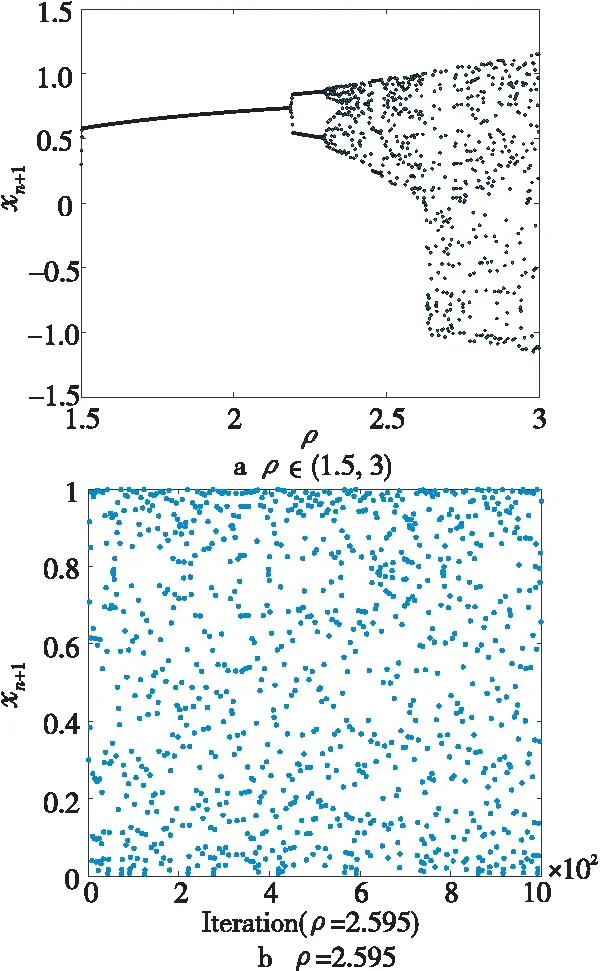
Figure 1 Cubic mapping图1 Cubic映射
3.2 非线性收敛因子
针对收敛因子a的调节,文献[1]采用的是线性控制策略,可表示如式(11)所示:
a0(t)=afirst-afirst·(t/Tmax)
(11)
其中,afirst为控制参数的初值。
从式(1)~式(8)可知,算法初期,较大的a值可保证全局搜索能力,随着迭代次数的增加,a的值逐渐减小,可加强算法的局部搜索能力。而式(11)中,a的值线性减小,不能很好地平衡算法的全局和局部搜索能力。为了提升算法搜索精度和速度,本文将使收敛因子随迭代次数的增加而呈非线性变化。
文献[15]对多种调整参数a的策略进行对比分析,并提出一种基于正弦函数的参数调整控制策略:
(12)
其中,afirst,afinal分别为控制参数的初值和终值;μ和k为调节参数,Tmax为最大迭代次数。
文献[15]对式(12)的参数进行了实验测试,当μ=k= 2时,改进策略的寻优效果优于其他改进策略(线性函数、二次函数和指数函数),故本文中设置μ= 2,k= 2,Tmax= 500。
各控制策略的仿真如图2所示。从图2中可以看出,不同的控制策略对算法的寻优过程有不同的影响,曲线的斜率表示算法寻优过程中的速度。本文的控制策略在前期的变化速度较慢,便于全局搜索;中期变化速度较快,便于提高搜索速度及跳出局部最优搜索;后期变化速度减缓,便于进入局部搜素,寻找最优解。
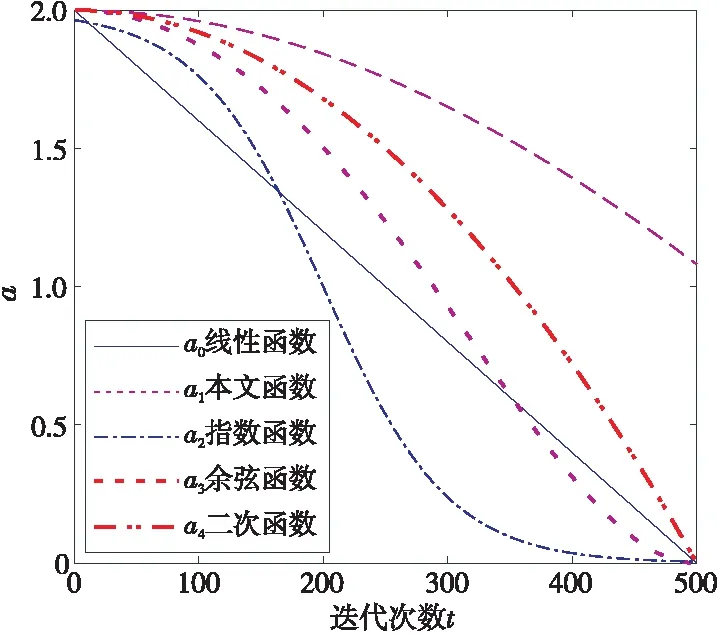
Figure 2 a vs. t in different control strategies图2 不同控制策略的控制参数随迭代次数的变化曲线
3.3 反向学习策略
反向学习策略[16]主要是对问题的可行解与反向解进行评价,选择较优的解作为下一代的优化个体,从而提高获得最优解的概率。其定义如下:
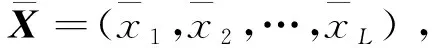
(13)

3.4 COGWO算法流程
本文提出的COGWO算法的实现步骤如算法1所示:
算法1COGWO算法
步骤1设置种群的规模N,维度dim,初始化a,A和C;采用Cubic映射式(10)初始化Xα,Xβ和Xδ的值。
步骤2根据寻优函数计算每个智能体的适应度值。
步骤3比较各智能体的适应度值以及Xα,Xβ和Xδ的适应度值,确定当前的最优解Xα,次优解Xβ和第3优解Xδ的值。
步骤4根据提出的非线性参数控制策略,由式(12)计算控制参数a的值,以及根据式(3)和式(4)分别计算A和C的值。
步骤5根据式(6)~式(8)更新种群个体的位置,再重新计算适应度值,并更新α,β和δ狼的值。
步骤6判断t是否达到Tmax,如果达到则结束,输出最优解;否则返回步骤2继续执行。
4 实验仿真与结果分析
4.1 实验设计与参数设置
为了验证COGWO算法的寻优性能及其有效性,本文设计了2组对比实验。(1)与经典的智能优化PSO算法[17]、较新的群体智能优化算法WOA (Whale Optimization Algorithm)[18]、改进的GWO算法(β-GWO(β-Chaotic map enabled Grey Wolf Optimizer)算法[9]和SOGWO(Selective Opposition based Grey Wolf Optimization)算法[11])进行对比实验; (2)与其他改进的GWO算法进行比较。
为了验证改进GWO算法的有效性,实验采用的基准测试函数如表1所示。其中,F1~F3为单峰函数,F4~F6为多峰函数。此外,本文寻优测试的实验环境为:Windows 7操作系统,Intel(R) Core(TM) i5-4210U CPU @2.4 GB,4 GB内存,Matlab 2018a。
本文的算法寻优中,各算法的参数设置如表2所示。种群规模N为30,最大迭代次数Tmax为500,维度dim为30。定义寻优成功率(Success rate)为ε=10-10,当寻优结果小于ε时,则认为寻优成功,反之为失败。
4.2 与标准的4种优化算法的比较
为验证本文提出的COGWO算法的性能,针对同一测试函数,每一种算法独立运行30次,并统计6种算法对6种基准测试函数寻优结果的平均值(Mean)、方差(Std)、寻优时间(Time)和寻优成功率(Success rate),结果如表3所示。

Table 1 Benchmark functions表1 基准测试函数

Table 2 Parameter settings表2 参数设置
从表3中可以看出,对于单峰测试函数F1~F3的寻优,除函数F1外,COGWO算法的寻优结果均优于其他5种群体智能优化算法的;对于多峰测试函数F4~F6的寻优,COGWO算法均优于PSO算法、GWO算法和改进GWO算法。对于测试函数F5的寻优,COGWO算法与WOA的结果相近;对于测试函数F6的寻优,本文提出的COGWO算法与β-GWO算法、SOGWO算法的结果相近,但COGWO算法的寻优时间较短。
从测试函数的寻优时间来看,COGWO算法均优于标准的GWO算法;从寻优成功率来看,COGWO算法的寻优成功率均为100%;从寻优的标准差来看,COGWO算法的标准差与寻优均值的数量级相差不大。这说明COGWO算法具有较好的寻优能力和稳定性,其收敛精度也比较高。
COGWO算法与5种群体智能优化算法对6种测试函数的寻优过程,如图3所示,图3a~图3f分别表示不同算法对6种测试函数的寻优曲线趋势。从图3中可以看出,COGWO算法明显优于GWO算法,且收敛速度更快,收敛精度更高。
4.3 与其他改进的GWO算法的比较
为进一步验证本文提出的COGWO算法的有效性,与文献[10]提出的LGWO (Grey Wolf Optimization algorithm based on Levy flight) 算法和文献[6]提出的CGWO (Grey Wolf Optimization based on nonlinear Convergence) 算法进行对比,结果如表4所示。其中“/”表示改进的算法未对该测试函数进行寻优测试。

Table 3 Comparison of optimization results with standard optimization algorithms表3 与标准优化算法的寻优结果对比
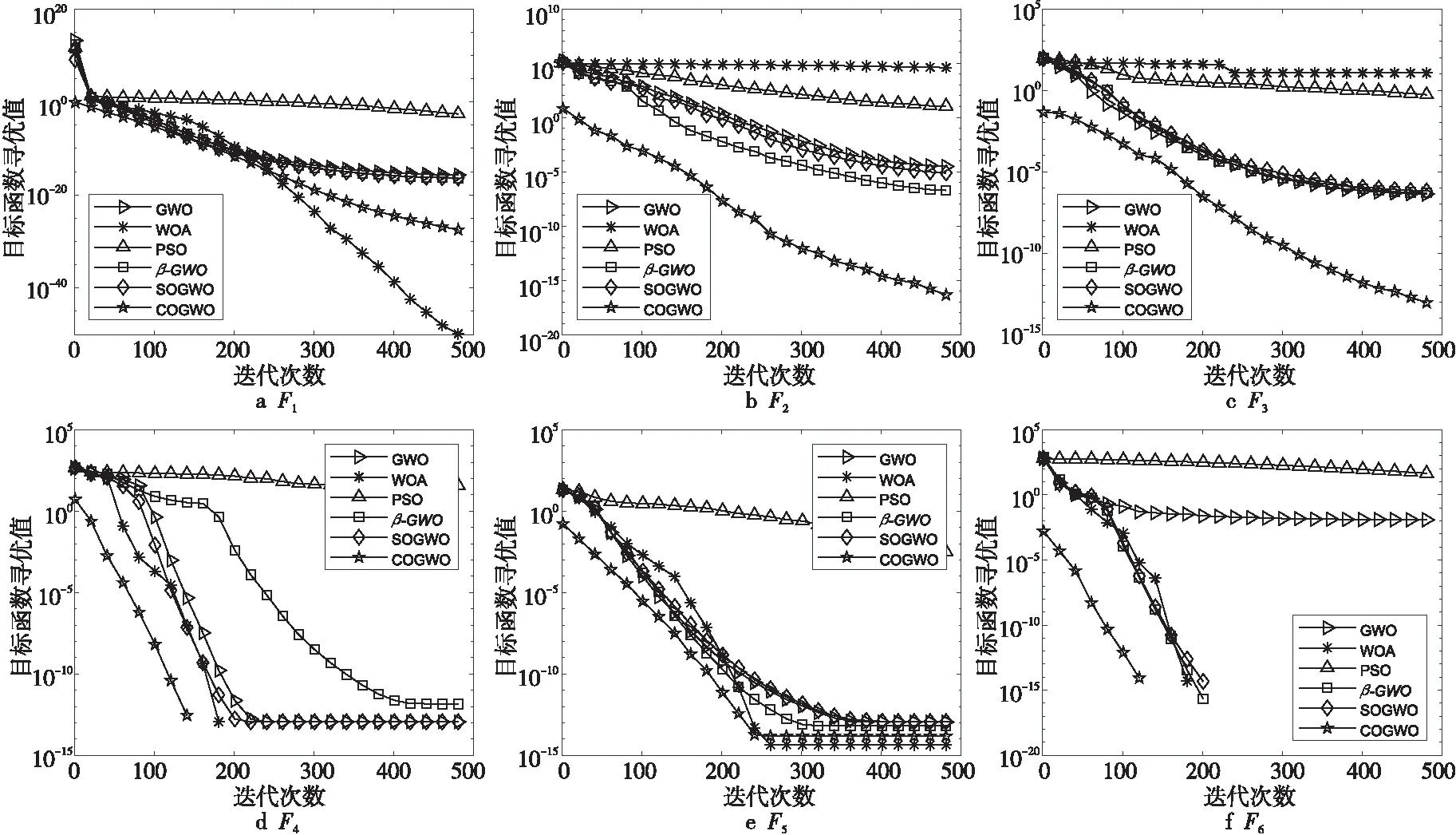
Figure 3 Fitness value curves of different algorithms图3 不同算法的寻优测试结果
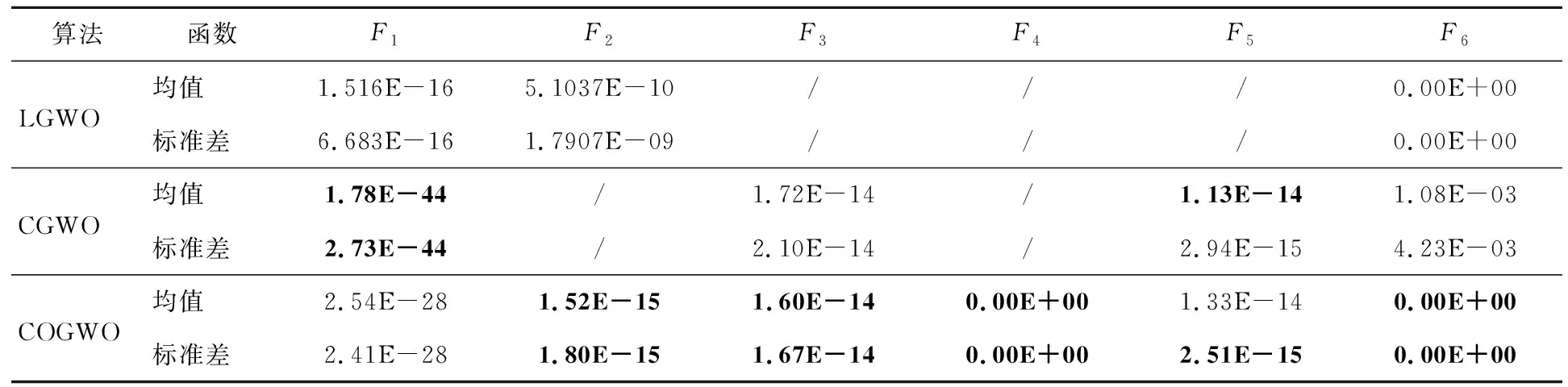
Table 4 Optimization comparison of optimized GWO algorithms
从表4中可以看出,对于函数F1的寻优,CGWO算法的寻优精度最佳,COGWO算法优于LGWO算法;对于函数F2的寻优,COGWO算法的寻优结果比LGWO算法的寻优结果高出5个数量级;对于函数F3和F5的寻优,COGWO算法与CGWO算法的均值结果相差不大,但从标准差来看,COGWO算法的稳定性更好;对于函数F6的寻优,COGWO算法和LGWO算法均优于CGWO算法。
5 工程优化问题应用
为了验证COGWO算法的性能,本节将其应用在拉压弹簧设计的工程问题中,并与GWO算法、PSO算法和WOA进行对比分析。
拉压弹簧设计问题是工程领域的一个经典的优化设计问题,在满足条件的前提下,要求弹簧的质量最小。此外,该设计问题主要包括3个变量:即弹簧的横截面的直径(d)、平均线圈的直径(Diam)和有源线圈的数量(Q)。
该问题的具体表述如式(14)所示:
X=[x1,x2,x3]=[d,Diam,Q]
(14)
目标函数如式(15)所示:
(15)
约束条件如式(16)所示:
(16)
其中,变量的取值范围如下所示:
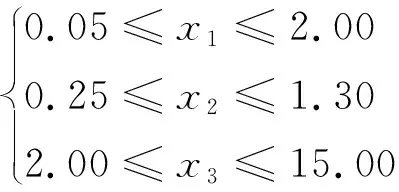
4种算法对拉压弹簧设计问题的实验结果如表5所示。
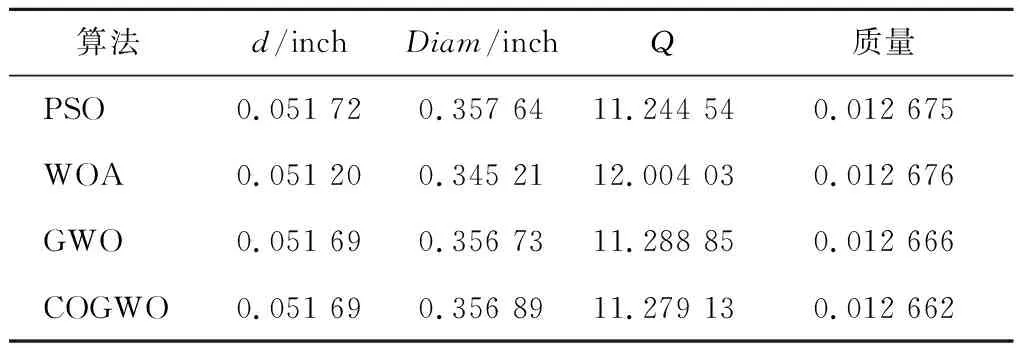
Table 5 Results of spring design problem by four optimization algorithms表5 4种优化算法的弹簧设计问题结果
从表5中可以看出,对于拉压弹簧设计问题,COGWO算法要略优于其他群体智能算法。此外,COGWO算法对于其他实际工程优化问题的应用效果的验证,还需要针对具体问题进行优化计算和实验。
6 结束语
本文针对标准的GWO算法对复杂优化问题的求解易陷入局部最优的缺点,从混沌初始化和非线性控制策略2个角度改进GWO算法,提出了一种基于Cubic映射和反向学习的GWO算法COGWO。通过混沌映射来增加初始种群的多样性,反向学习策略和非线性控制参数策略用来改进算法的收敛速度,并提高算法的收敛精度。与5种群体智能算法对6种基准测试函数进行寻优实验,寻优结果表明,与对比算法相比COGWO算法的寻优能力和收敛精度得到一定的提高,且稳定性增强。此外,本文的COGWO算法与LGWO算法和CGWO算法相比,稳定性较好,寻优精度也较高,在实际的工程优化问题中也有较好的应用。未来将COGWO算法应用到更多的实际工程优化问题中,且对COGWO算法的收敛性理论证明开展进一步的研究。
