带形状参数的三次三角域Bézier曲面*
2021-11-22查东东刘华勇王曾珍
查东东,刘华勇,王曾珍
(安徽建筑大学数理学院,安徽 合肥 230601)
1 引言
在计算机辅助几何设计中,三角域上非张量积型的Bézier曲面因为在形状设计上的灵活性,得到了大量的应用。同时学术界为克服它在控制多边形不变时不能调整曲面外形的缺点,引入了形状参数。例如,文献[1]构造了三角域上的局部形状可调的三次Bézier曲面;文献[2]从几何角度定义了带形状参数的四次Bézier曲面;文献[3]在不升次的前提下,扩展了三角域上的三次Bézier曲面;文献[4]分析了三角域上生成三角多项式曲面的方法。文献[1-4]中的曲面除了继承原有的特性,还能利用形状参数来调节曲面的形状,但上述曲面还存在着不能兼顾局部形状参数和全局形状参数的缺点。文献[5]讨论了带有3个形状参数的三角曲面;文献[6]介绍了三角域上二元n次Bernstein基函数的扩展;文献[7]给出了针对空间散乱数据点的三次曲面插值方法;文献[8]给出了带多局部形状参数的拟二次Bernstein基函数。文献[5-8]中曲面的构造,都未实现拼接的连续性,且文献[5]的局部形状参数和全局形状参数效果是非独立的,或对曲面的形状控制力还略有不足。文献[9]将指数函数合并到多项式函数中;文献[10]基于递推关系构造了带形状参数的基函数;文献[11]扩展了带有多个形状参数的Bézier曲线和曲面。
本文构造了带有形状参数的三次三角域Bézier曲面,构造出的曲面不但能实现较高的光滑拼接,还可以用3个局部形状参数和1个全局形状参数修改曲面形状,其中,3个局部形状参数取值相同时具有对称性的形状控制效果。形状参数大大丰富了曲面的形状控制效果。
2 带形状参数的三次三角域Bernstein基函数
2.1 基函数的定义
定义1给定面积坐标(u,v,w),其中,u,v,w≥0,u+v+w=1,称:
(1)
为带形状参数λ,α1,α2,α3的三次三角域Bernstein基函数,简称为三次三角域λα-Bernstein基。其中,-2<λ≤1,0≤α1,α2,α3≤1。
2.2 基函数的性质
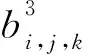
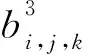
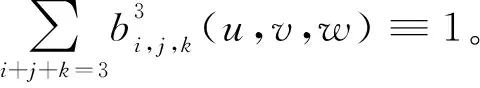
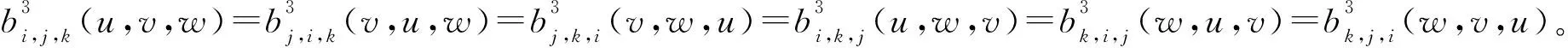
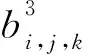
性质5(角点性质) 当i+j+k=3时,有:
性质6(角点导数)
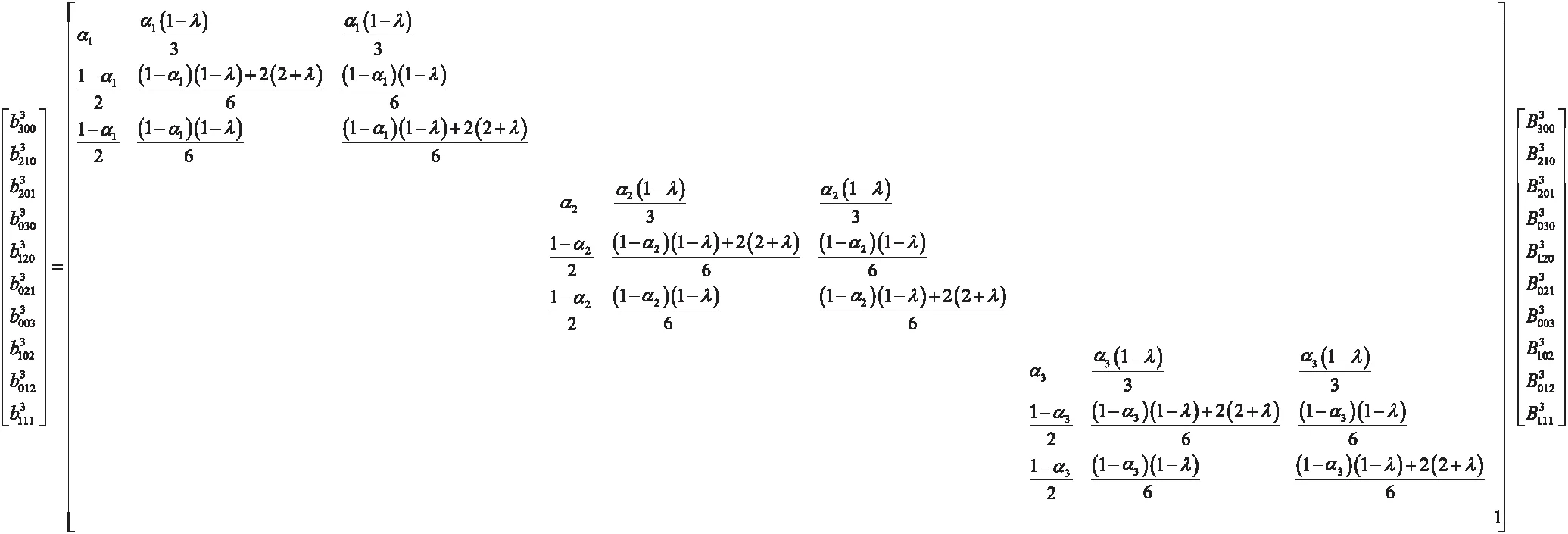
(2)
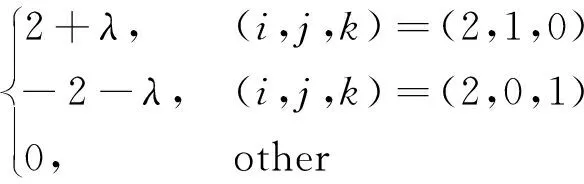
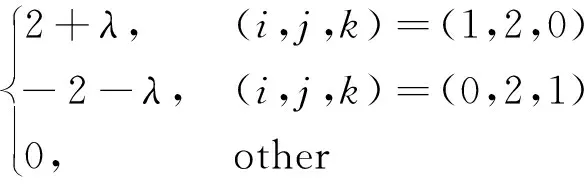
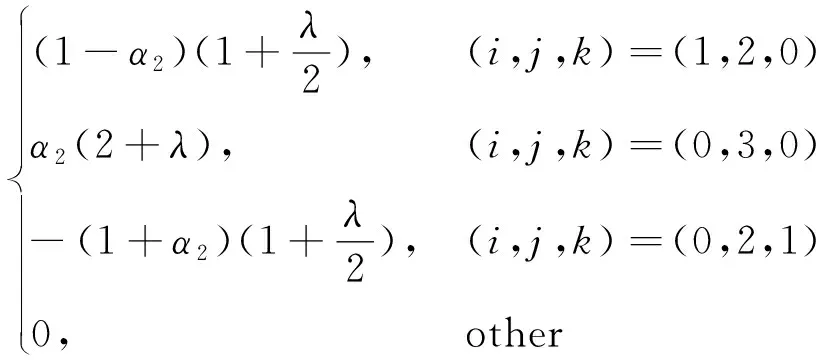
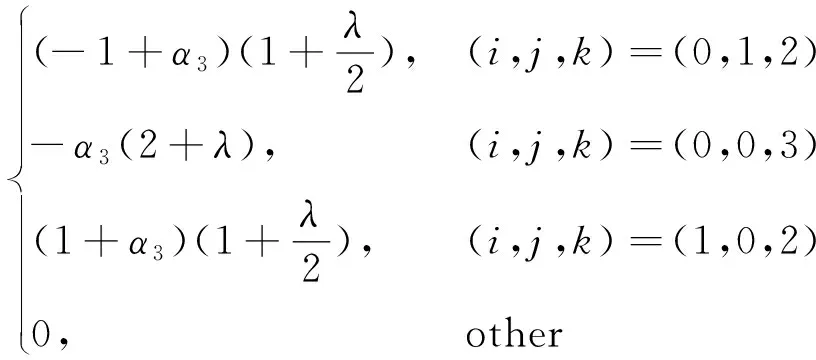
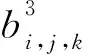
证明若
(3)
其中,Xi,j,k∈R。将式(2)代入式(3)整理得:

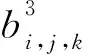
□
3 带形状参数的三次三角域Bézier曲面
3.1 三次三角域λα-Bézier曲面
定义2给定面积坐标(u,v,w),其中u,v,w≥0,u+v+w=1,呈三角阵列的控制顶点Pi,j,k(i,j,k≥0,i+j+k=3)∈R3,称:
(4)
为带形状参数α1,α2,α3,λ的三次三角域Bézier曲面,简称为三次三角域λα-Bézier曲面。
借由转换矩阵,也可将r*(u,v,w)写作三次三角域Bézier曲面形式:
(5)
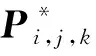
(6)
3.2 三次三角域λα-Bézier曲面性质
性质8(凸包性) 三次三角域λα-Bézier曲面完全被包含在控制点Pi,j,k构成的凸包内。
性质9(几何不变性和仿射不变性) 三次三角域λα-Bézier曲面的形状仅依赖于控制顶点Pi,j,k∈R3(i,j,k≥0,i+j+k=3),几何变换不改变曲面的形状。
其中,N是任意向量且N∈Rd(d=3),M是一任意k×k(k=3)阶矩阵。
性质10(角点性质) 当i+j+k=3时,有:
性质11(退化性) 当α1=α2=α3=λ=1时,三次三角域λα-Bézier曲面退化为三次三角域Bézier曲面。
性质12(形状可调性) 当Pi,j,k(i,j,k≥0,i+j+k=3)固定时,可以改变形状参数α1,α2,α3,λ的值来控制曲面的形状。
图1为给定同一控制点Pi,j,k下,形状参数α1,α2,α3,λ分别取不同值时得到的三次三角域λα-Bézier曲面。可以看出各参数的效果:
(1)λ趋于1 时,曲面整体就越靠近控制网格,如图1a~图1c所示。

Figure 1 Influence of different values of λ,α1,α2 and α3 on the surface图1 λ、α1、α2、α3分别取不同值时对曲面的影响
(2)α1、α2、α3控制效果是类似的,这也与基函数的性质3相对应。它们各自控制着相应角点处的局部曲面形状,是对称的。其中α1控制着角点P300的局部曲面形状,α1越趋于0,P300的局部曲面越靠近线段P210P201。α1越趋于1,P300处的局部曲面越靠近P300,如图1d~图1f所示。同理可得:α2控制着角点P030的局部曲面形状,α2越趋于0,P030的局部曲面越靠近线段P120P021。α2越趋于1,P030处的局部曲面越靠近P030,如图1g~图1i所示。同理可得:α3越趋于0,P003的局部曲面越靠近线段P012P102。α3越趋于1,P003处的局部曲面越靠近P003,如图1j~图1l所示。
3.3 n次三角域λα-Bézier曲面
借助De Casteljau算法可以递推n(n≥4)次三角域λα-Bernstein基函数[1]:
(7)
定义3给定面积坐标(u,v,w),其中u,v,w≥0,u+v+w=1,呈三角阵列的控制顶点Pi,j,k(i,j,k≥0,i+j+k=n)∈R3,称:
(8)
为带形状参数α1,α2,α3,λ的n次三角域Bézier曲面,简称为n次三角域λα-Bézier曲面。
3.4 三角域λα-Bézier曲面与类似方法的比较
本文将λα-Bézier曲面与文献[11]中扩展的Bézier曲面进行了如下比较:
(1)以控制网格为目标函数,引入2-范数来衡量曲面到控制网格的距离,2-范数越小,距离越短,逼近程度越高。
当λα-Bézier曲面比文献[11]中扩展Bézier曲面更贴近控制网格时,有:
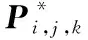
(2)比较文献[11]算法和本文算法的时间复杂度,借助Matlab秒表计时函数计算出各种算法的运行时间,以运行时间近似替代。为减少误差算法运行时间按如下方式统计:每种算法一组实验执行100次循环,取100次运行时间的平均值,进行10组实验,再取10组平均运行时间的最优值,比较2种算法的运行时间最优值。多次实验后可以看出,改进算法略有领先,但基本上两者相差不大。
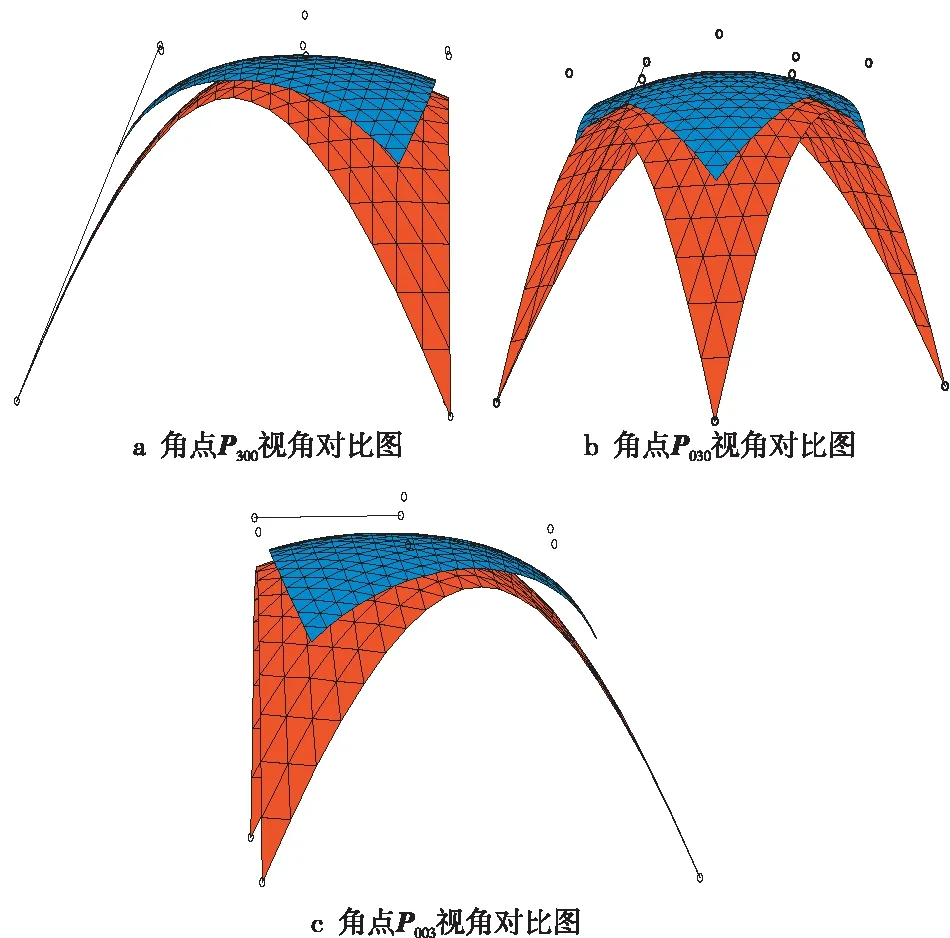
Figure 2 Comparison of curved surfaces from different angles图2 不同角点视角曲面对比图
(3)λα-Bézier曲面和文献[11]中扩展Bézier曲面都能全局和局部地修改形状,但λα-Bézier曲面具有全局形参和局部形参,文献[11]中曲面形状的全局修改还是依靠共同修改多局部形参,且参数过多。
算法对比如表1所示。
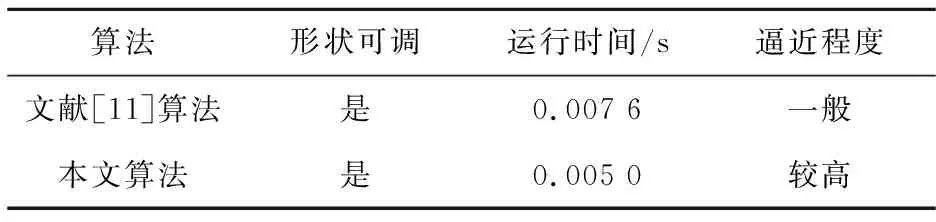
Table 1 Comparison of different algorithms表1 不同算法的对比
4 曲面拼接
4.1 三次三角域Bézier曲面的C1连续拼接
给定2张三次三角域Bézier曲面
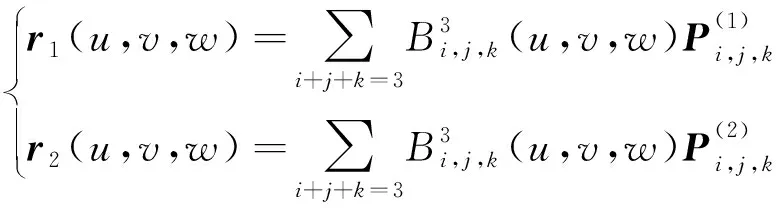
由三角域Bézier曲面的拼接条件[12]知,若满足:
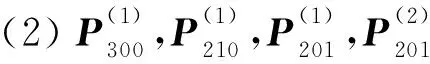
则2张三次三角域Bézier曲面r1(u,v,w)和r2(u,v,w)在公共边界(w=0)实现C1连续。
4.2 三次三角域λα-Bézier曲面的C1连续拼接
定理1给定2张三次三角域λα-Bézier曲面
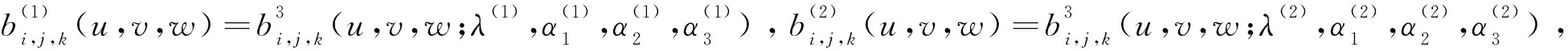
若满足:
(1)α1=α2=λ=1;
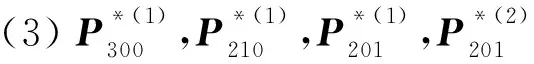
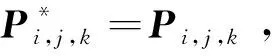
□

Figure 3 Jointing of cubic triangular λα-Bézier surfaces图3 三次三角域λα-Bézier曲面的C1拼接
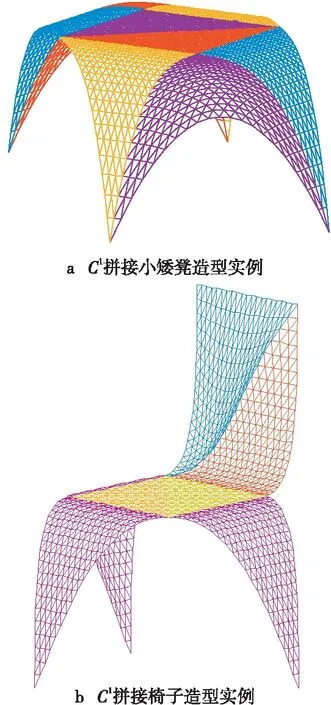
Figure 4 Examples of λα-Bézier surface jointing around corner points图4 λα-Bézier曲面绕角点的C1拼接实例
4.3 三次三角域Bézier曲面的G1连续拼接
给定2张三次三角域Bézier曲面:
(9)
其中,Qi,j,k为曲面r2(u,v,w)上的点坐标。
由三角域Bézier曲面的拼接条件[11]知:
当i,j≥0,i+j+k=3时满足:
P0,j,k=Q0,j,k
(10)
有r1(0,v,w)=r2(0,v,w),即2张三次三角域Bézier曲面r1(u,v,w)和r2(u,v,w)在公共边界(u=0)实现G0连续;
实现G1连续需在式(10)基础上还满足:
(11)
其中,ε和η为自由因子。
式(10)可转化为:
(12)
则同时满足式(10)和式(12)时,r1(u,v,w)和r2(u,v,w)在公共边界(u=0)实现G1连续。
4.4 三次三角域λα-Bézier曲面的G1连续拼接
给定2张三次三角域λα-Bézier曲面:
(13)
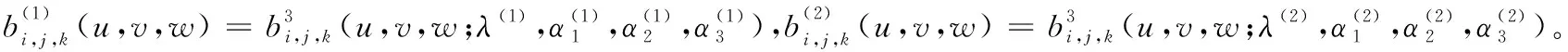

Figure 5 Jointing of cubic triangular λα-Bézier surfaces图5 三次三角域λα-Bézier曲面的G1拼接
又可以将式(13)改写为:
(14)
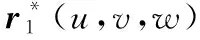
当i,j≥0,i+j+k=3时满足:
(15)
(16)
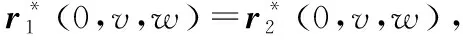
将式(6)和式(16)代入式(14)可得:
(17)
实现G1连续需在式(17)基础上还满足:
(18)
将式(6)、式(17)代入式(18)可得:
(19)
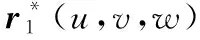
5 结束语
本文构造了带有形状参数的三次三角域Bézier曲面,在继承三次三角域Bézier曲面原有性质外,曲面满足C1、G1连续的融合条件也比较简单,文中给出了一些参数不同取值下的曲面形状可调的实例。此外,本文在保持基函数次序不变的情况下,给出了可调的局部形状参数和全局形状参数,可以根据需求更方便地调节曲面的形状。
