一种部分流水的多塔三维SoC测试时间优化算法*

邵晶波，王 丹，王 岩，张瑞雪

(1.哈尔滨师范大学计算机科学与信息工程学院，黑龙江 哈尔滨 150025； 2.哈尔滨金融学院计算机系，黑龙江 哈尔滨 150030)

1 引言

随着半导体工业制造技术不断发展，集成电路已进入超越摩尔定律时代。国际半导体技术路线图ITRS(International Technology Roadmap for Semiconductors)预测，到2021年，晶体管尺寸将不再缩小，传统的二维SoC已不能解决因互连线过长、功耗过高等问题而面临的严峻挑战，采用垂直硅通孔TSV(Through Silicon Via)技术的三维SoC由于缩短了互连长度，减少了电路延迟，提高了系统集成度和系统性能，已成为业界研究的热点。从中长期来看，基于TSV的晶片堆叠将占主要地位，而测试工作将面临的挑战之一为，需要一种新的可测性设计方法来缓解增加的测试仪测试时间和测试资源问题[1]。

与传统二维芯片不同，三维SoC测试分绑定前、绑定中、绑定后和封装[2]。绑定中测试指每新堆叠一层晶片就要对这个部分堆叠整体测试一次。它能更早地检测出三维SoC绑定中引入的缺陷，但会导致测试时间剧增[3]，热量分布不均[4]，测试成本高[5]等问题。若绑定中某一晶片或TSV出现缺陷，将导致所有晶片或TSV失效，则成品率下降。此外，IP核复用技术虽可使三维SoC开发周期缩短，但它自身不能访问嵌入式核。因此，三维SoC因良率损失和测试困难导致其测试优化更加困难而成为主要挑战[6]。如今，以测试封装和测试访问机制TAM(Test Access Mechanism)为架构的模块化测试已经成为三维SoC测试的主要方法。首先通过测试封装将不同IP核的I/O接口标准化，TAM通过I/O引脚传输测试数据，而且层间连接需有测试专用TSV。三维SoC测试资源优化涉及测试成本优化，而测试时间影响测试成本，本文主要研究多塔三维SoC绑定中测试时间TT(Test Time)优化问题。

文献[7]为平衡测试时间和TAM带宽，提出适用于硬、软晶片的维克瑞-克拉克-格罗夫斯VCG(Vickrey-Clarke-Groves)算法，把测试时间和TAM带宽看作博弈双方，达到了全局和个体最优目标，但未考虑测试功耗。原始的IEEE P1838标准提案只针对单塔三维SoC测试，而比利时微电子研究中心IMEC(Interuniversity MicroElectronics Centre)的Chi等人[8]首先提出经济有效且可扩展的多塔通用架构，它符合IEEE 1149.1/1500标准，塔可包含任意数量晶片，塔内分包含子塔和不包含子塔2种，其架构与IEEE P1838标准提案相同。本文主要研究的多塔三维SoC正是该架构的扩展。随后，Papameletis等人[9]提出支持测试数据压缩、嵌入式IP核和多塔堆叠的三维SoC，为后续研究打下了良好基础。针对测试时间长的问题，印度理工学院的Dhuwalia等人[10]提出考虑测试引脚和TSV约束的适用于硬晶片的逐层LBL(Layer-By-Layer)算法、逐塔TBT(Tower-By-Tower)算法和启发式HA(Heuristic Algorithm)算法，但是没有考虑测试功耗，且没有最大限度地减少空闲时间块，因而有进一步优化的空间。文献[11]针对多塔三维SoC测试时间长的问题，提出适用于硬晶片的基于无会话的多塔三维SoC测试调度方法，但没有考虑测试功耗。文献[12]在TAM带宽和TSV数、峰值功耗约束下，对多塔三维ICs绑定后测试和集成过程总测试采用量子粒子群算法调度优化。

针对这些问题，本文提出同时考虑TAM带宽、层间TSV数和测试功耗约束的多塔三维SoC测试时间优化算法。

本文其余部分组织如下：第2节描述本文所研究的问题；第3节分析HA的不足；第4节详细介绍本文提出的多塔三维SoC测试时间优化算法；第5节是实验结果及分析，以检验本文算法的优点；最后总结全文。

2 问题描述

三维SoC可嵌入2～8个晶片，本文只讨论由硬晶片(测试架构固定、测试时间已知) 实现的多塔三维SoC。测试三维SoC时，TAM需经最底层晶片上的测试引脚把测试数据扩展至所有晶片，将测试激励传送到被指定晶片或将测试响应传送到最底层测试引脚，除最底层晶片外，所有晶片都需有测试专用TSV，也称“测试梯”。

多塔三维SoC中除最底层晶片外，其余晶片所在塔的塔底晶片只有一个，其塔内分包含子塔和不包含子塔2种。本文所研究的是塔内包含子塔的多塔三维SoC。

图1中的矩形表示晶片，最底层晶片1的底部是I/O引脚，晶片内部的水平箭头是TAM，晶片之间的垂直箭头是TSV连接。图1所示粗实线框内整体为一个多塔三维SoC，由6个晶片、2个塔组成，2个塔都位于晶片1上，分别为细实线框内的塔1和塔2。塔1由晶片2和晶片4组成，是塔内不包含子塔的塔；塔2由晶片3、晶片5和晶片6组成，为塔内包含2个子塔的塔，2个子塔都位于晶片3上，即虚线框内的子塔21和子塔22。其中，子塔21由晶片5构成，子塔22由晶片6组成。

Figure 1 Architecture illustration of multi-tower 3D SoC图1 多塔三维SoC结构示例

一个测试引脚所占面积大约是一个TSV的百倍[13]。每个晶片都内嵌多个IP核，其I/O引脚数与IP功能复杂程度成正比，而特定晶片对外测试引脚数有限，所以测试时应考虑可用测试引脚数。

由于TSV通常用于时钟、电源/接地和I/O等功能互连，测试访问专用的TSV数不能太多[14]。而且，TSV面积开销大，制造成本高，因此测试时应考虑TSV数约束[15]。

集成电路测试时会激活晶片各功能模块，其产生的测试功耗值和电路跳变次数都高于正常模式。但是，晶片垂直堆叠不易散热，可能会使电路不能正常工作，严重时会烧毁电路。因此，三维SoC测试必须考虑测试功耗，比如通过限定哪些晶片并行测试，哪些晶片串行测试来保护待测电路。

多塔三维SoC测试时间优化问题描述如下：

给定一个塔内包含子塔的多塔三维SoC，由M个晶片、N个塔构成。假设最底层晶片上可用测试引脚数为Wmax，峰值功耗为Pmax，层间TSV数上限为L.TSVmax。对于任意晶片i∈{1,2,…,M}，其测试时间为Diei.t，测试引脚数为Diei.w(Diei.w≤Wmax)，测试功耗为Diei.p。目标为在Wmax、Pmax和L.TSVmax约束下，寻求最佳的测试方法，使总测试时间TT最小。

3 HA的不足

针对多塔三维SoC测试时间优化问题，文献[10]提出了考虑测试引脚和TSV约束的LBL、TBT和HA算法，其中HA是经典算法，优化效果最好、性能最高，然而HA也存在不足，仍有优化空间。

基于表1和图2，假设Wmax=60，L.TSVmax=100，利用文献[10]的HA所得TT为550。

Table 1 Parameters for hard dies表1 硬晶片参数表

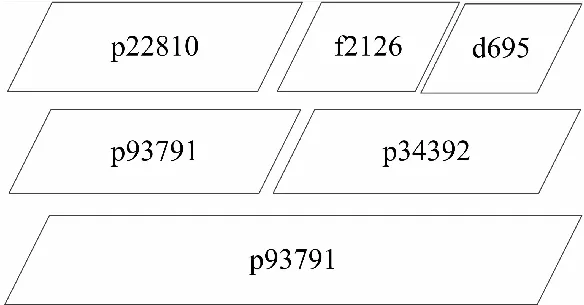
Figure 2 Multi-tower 3D SoC图2 多塔三维SoC

图3利用为HA的多塔三维SoC测试过程[10]，不难看出，它是等待上一个并行晶片子集测试完后，再去寻找下一个并行晶片子集，每个并行晶片子集的测试时间取决于测试时间最长的晶片，整个过程产生很多空闲时间块，并没有使测试时间达到最优。

Figure 3 Test process of HA 图3 HA测试过程

下面针对文献[10]的HA产生空闲时间块，没有最大程度优化测试时间的缺点，举例进行改进。

基于表1和图2，假设Wmax=60，L.TSVmax=100。

所有晶片初始化为未测试，按测试时间降序排列为p34392、p93791、p93791、p22810、f2126和d695。

(1)选择p34392，但p34392所在位置对应的底层p93791未测试，则选择p93791， p93791所占Wmax=30，位于第0层，使用TSV=0(最底层晶片不使用TSV)，测试结束时间为200并标记为已测试，当前剩余Wmax=30且第0层TSV=100。

(2)选择p34392，p34392所占Wmax=25，位于第1层，使用TSV=50，测试结束时间为250并标记为已测试，当前剩余Wmax=5且第1层TSV=100-50=50。

(3)选择p93791(位于第1层)，p93791所占Wmax=30>5，释放最早结束测试时间为200的p93791所占测试资源并移除该时间，当前剩余Wmax=35且第0层TSV=100，则再选择p93791；p93791所占Wmax=30，位于第1层，使用TSV=60>50,释放最早结束测试时间为250的p34392所占测试资源并移除该时间，当前剩余Wmax=60且第1层TSV=50+50=100，则再选择p93791;p93791所占Wmax=30，位于第1层，使用TSV=60，测试结束时间为250+200=450并标记为已测试，当前剩余Wmax=30且第1层TSV=100-60=40。

(4)选择p22810，p22810所占Wmax=25，位于第2层，使用TSV=50，测试结束时间为250+150=400并标记为已测试，当前剩余Wmax=5且第2层TSV=100-50=50。

(5)选择f2126，f2126所占Wmax=20>5，释放最早结束测试时间为400的p22810所占测试资源并移除该时间，当前剩余Wmax=30且第2层TSV=50+50=100，则再选择f2126;f2126所占Wmax=20，位于第2层，使用TSV=40，测试结束时间为400+100=500并标记为已测试，当前剩余Wmax=10且第2层TSV=100-40=60。

(6)选择d695，d695所占Wmax=15>10，释放最早结束测试时间为450的p93791所占测试资源并移除该时间，当前剩余Wmax=40且第1层TSV=60+40=100，则再选择d695；d695所占Wmax=15，位于第2层，使用TSV=30，测试结束时间为450+50=500并标记为已测试，当前剩余Wmax=25且第2层TSV=60-30=30。

(7)此时所有晶片已测试完，TT=500。

由此可见，对于同一个多塔三维SoC，相同约束下，改进HA后的TT为500，比文献[10]的HA所得TT更优。

图4为改进HA后的测试过程，可以看出，改进算法明显减少了空闲时间块，缩短了TT。在此基础上，本文提出基于硬晶片的多塔三维SoC测试时间优化算法。

Figure 4 Reduced test time for the improved HA 图4 改进HA的测试时间优化

4 多塔三维SoC测试时间优化

测试功耗是影响测试时间的重要因素之一，文献[10]算法不但产生了空闲时间块，而且没有考虑测试功耗。根据以上分析，本文提出新型多塔三维SoC测试时间优化算法，该算法不但考虑测试引脚和TSV数约束，还考虑测试功耗。

4.1 变量定义

表2为本文提出的多塔三维SoC测试时间优化算法所涉及的变量定义。

Table 2 Variable definitions of the proposed algorithm表2 本文算法中变量的定义

4.2 算法流程

图5为多塔三维SoC测试时间优化算法流程。将所有晶片初始化为未测试，并按测试时间降序排列。优先选择测试时间最长的晶片，同时遵循自底向上的选择原则。综合考虑Wmax、L.TSVmax和Pmax3种测试资源，每测试一个晶片，记录剩余测试资源和测试结束时间，并标记为已测试。同时再把剩余未测试晶片降序排列后，按原则选择晶片。直到剩余测试资源不满足待调度晶片测试时，释放第1个最早结束测试的晶片测试资源(释放的TSV资源指相应层的TSV数)，再判断剩余测试资源是否满足待调度晶片测试。若满足，则待调度晶片提前进入测试阶段，使该晶片与未结束测试晶片实现部分流水，否则再释放第2个最早结束测试的晶片测试资源。以此类推，直至所有晶片测试完毕。

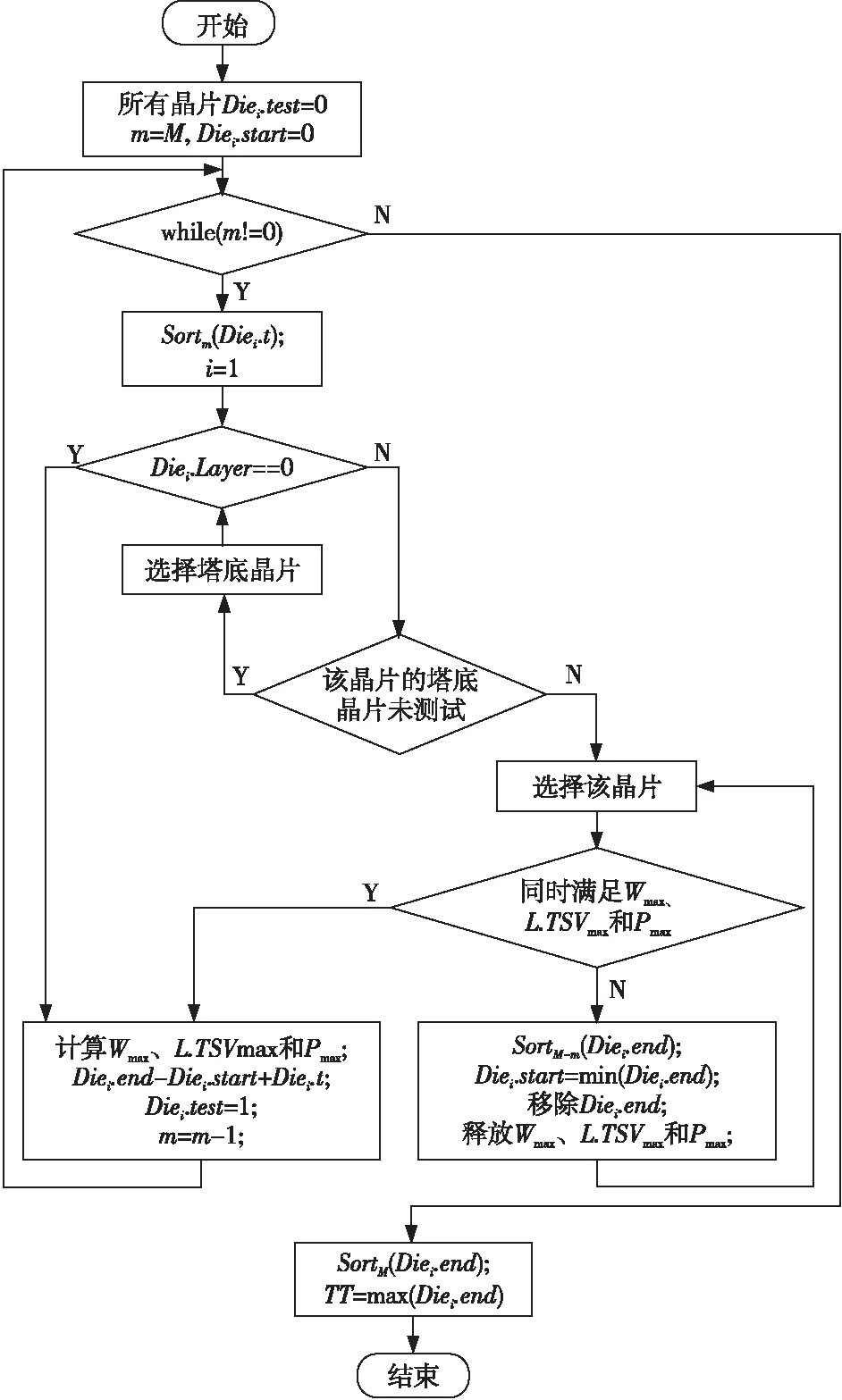
Figure 5 Flow chart of the proposed algorithm图5 本文算法流程图

本文提出的多塔三维SoC测试时间优化算法如算法1所示。

算法1新型多塔三维SoC测试时间优化

输入：表1中的变量。

输出：最佳测试时间TT。

1.begin

2.M个晶片初始化为Diei.test=0;m=M;Diei.start=0;

3.while(m!=0) {

4.m个晶片按Diei.t降序排列;

5.i=1;//选择第1个未测试晶片

6.if(Diei.layer==0){

7.Wmax=Wmax-Diei.w;

8.Pmax=Pmax-Diei.p;

9.Diei.tsv=0;

10.L.TSVmax=L.TSVmax-Diei.tsv;

11.Diei.end=Diei.start+Diei.t;

12.Diei.test=1;

13.m=m-1}

14.else{

15.if(该晶片所在的塔底晶片未测试){

16. 选择塔底晶片，判断是否位于第0层}

17.else{

18. 选择该晶片;

19.if(Diei.w<=Wmax&&Diei.p<=Pmax&&2*Diei.w<=L.TSVmax){

20.Wmax=Wmax-Diei.w;

21.Pmax=Pmax-Diei.p;

22.Diei.tsv=2*Diei.w;

23.L.TSVmax=L.TSVmax-Diei.tsv;

24.Diei.end=Diei.start+Diei.t;

25.Diei.test=1;

26.m=m-1}

27.else{

28.SortM-m(Diei.end);

29.Diei.start=min(Diei.end);

30.RemoveDiei.end

31.Wmax=Wmax+Diei.w;

32.Pmax=Pmax+Diei.p;

33.L.TSVmax=L.TSVmax+Diei.tsv;

34.选择该晶片，判断此时剩余测试资源是否满足该晶片测试}}}}

35.SortM(Diei.end);//排序所有晶片

36.returnTT=max(Diei.end);

37.end

本文提出的多塔三维SoC测试时间优化算法中，while循环体的量级是m，所以时间复杂度为O(m)；算法没有利用辅助空间，辅助空间是常量，因此空间复杂度是O(1)。其中第2行是将所有晶片初始化为未测试。第3～34行是测试调度所有晶片，直到测试所有晶片后退出循环。第28～34行是释放最早结束测试的晶片测试资源，让待测试晶片提前进入测试，使该晶片与未结束测试晶片部分重叠并行，实现部分流水测试。第34～35行是返回所有晶片结束测试时间中的最大值作为TT。

5 实验与结果分析

本文在内存为4 GB、主频是2.4 GHz的英特尔双核处理器Windows 10操作系统上，采用C语言编程实现所提算法。为验证所提算法的有效性，选用ITC02测试基准中的d695、f2126、p22810、p34392和p93791 5种晶片，手工搭建图6所示的2类多塔三维SoC，以此为例进行实验。表3为所选晶片的参数，假设全为硬晶片，其测试时间和测试引脚引自文献[10]，测试功耗引自文献[12]。

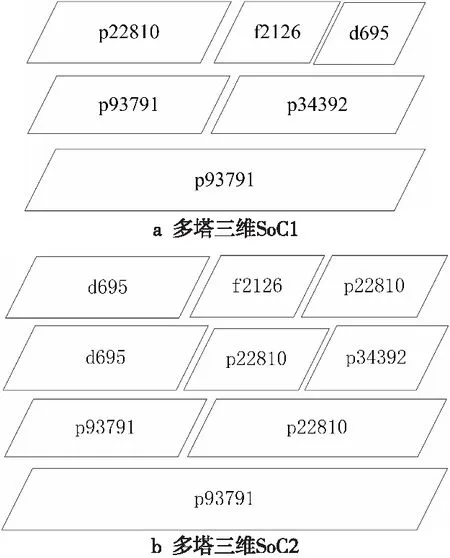
Figure 6 Two kinds of multi-tower 3D SoC图6 2种多塔三维SoC

5.1 考虑TAM带宽和层间TSV数约束

为考察测试引脚和TSV数对多塔三维SoC总测试时间的影响，这组实验暂时忽略测试功耗。表4和表5分别为考虑TAM带宽和TSV数约束时，本文算法与文献[10]的HA、TBT、LBL算法在多塔三维SoC1和多塔三维SoC2上的测试时间结果比较。表4和表5中第1、2列的Wmax和L.TSVmax分别为可用测试引脚数和TSV数；第3列又都分为4小列，用以表示本文算法与HA、TBT、LBL算法各自所得的测试时间；第4、5、6列分别表示本文算法相比HA、TBT、LBL算法在测试时间方面减少的百分比。

Table 3 Parameters for selected hard dies表3 选定硬晶片的参数

从表4可以看出，对于多塔三维SoC1测试时间，与HA相比，本文算法减少率达到20.34%；与TBT算法相比，本文算法减少的测试时间达到54.68%；与LBL算法相比，本文算法减少率达到58.96%。

表5表明，针对多塔三维SoC2的测试时间，与HA相比，本文算法减少率达到27.78%；与TBT算法相比，本文算法减少的测试时间达到41.04%；与LBL算法相比，本文算法减少率达到68.87%。

Table 4 Comparison of TT among the proposed algorithm and HA、TBT、LBL on 3D SoC1表4 本文算法与HA、TBT、LBL算法的多塔三维SoC1测试时间比较

Table 5 Comparison of TT among the proposed algorithm and HA、TBT、LBL on 3D SoC2表5 本文算法与HA、TBT、LBL算法的多塔三维SoC2测试时间比较

同一测试引脚和TSV数约束下，相比于HA、TBT和LBL算法，本文算法所得的多塔三维SoC总测试时间都更短，因而测试时间优化性能更好。

根据表4和表5，得到图7～图10。图7和图9分别为当给定Wmax=120，改变多塔三维SoC1和多塔三维SoC2的L.TSVmax值时，本文算法与HA、TBT、LBL算法的TT变化比较。类似地，图8和图10分别绘出了当给定L.TSVmax=140，改变多塔三维SoC1和多塔三维SoC2的Wmax值时，本文算法与HA、TBT、LBL算法的TT变化比较。

Figure 7 TT of multi-tower 3D SoC1 varying with L.TSVmax when Wmax=120图7 Wmax=120时多塔三维SoC1随L.TSVmax变化的TT

Figure 8 TT of multi-tower 3D SoC1 varying with Wmax when L.TSVmax=140图8 L.TSVmax=140时多塔三维SoC1随Wmax变化的TT

Figure 9 TT of multi-tower 3D SoC2 varying with L.TSVmax when Wmax=120图9 Wmax=120时多塔三维SoC2随L.TSVmax变化的TT

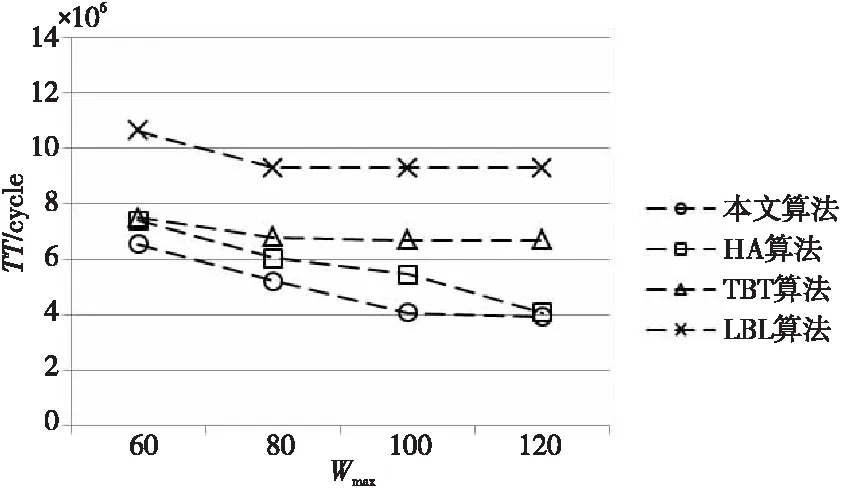
Figure 10 TT of multi-tower 3D SoC2 varying with Wmax when L.TSVmax=140图10 L.TSVmax=140时多塔三维SoC2随Wmax变化的TT

图7～图10显示，无论是改变Wmax还是L.TSVmax，本文算法所得TT都小于HA、TBT、LBL算法的，表明本文算法在测试时间优化方面，都优于HA、TBT、LBL算法。是因为本文算法通过释放最早结束测试的晶片测试资源，让待调度晶片提前进入测试阶段，在刚进入测试阶段的晶片与测试还未结束的晶片之间实现了部分流水，减少了并行测试过程中的空闲时间块，从而使TT大大缩短。

根据表4和表5，本节绘出了图 11和图12，比较了测试引脚数和TSV数对多塔三维SoC测试时间的影响。

Figure 11 Influence of Wmax and L.TSVmax on TT of multi-tower 3D SoC1图11 Wmax和L.TSVmax对多塔三维SoC1的TT的影响

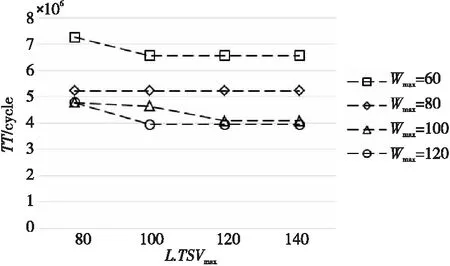
Figure 12 Influence of Wmax and L.TSVmax on TT of multi-tower 3D SoC2 图12 Wmax和L.TSVmax对多塔三维SoC2的TT的影响

以图11中Wmax=60时，多塔三维SoC1测试时间随L.TSVmax变化的趋势为例。在Wmax为60的条件下，当横坐标L.TSVmax小于120时，纵坐标上测试时间在减少；当L.TSVmax达到120时，测试时间保持不变。其本质原因是当测试引脚数不变时，测试时间会随TSV数的增加而减少，这是因为增加TSV数相当于增加测试资源量；但当TSV数增加到某一特定值时，测试时间不再改变，表明此时测试时间不再受TSV数影响，而是受测试引脚数影响。

同样，以L.TSVmax=120为例，测试时间随Wmax的增加在减少；以L.TSVmax=80为例，当Wmax分别为60,80,100和120时，测试时间无变化。其原因为当给定TSV数时，测试时间会随TAM带宽的增加而减少，这是由于增加TAM带宽，可供并行测试的核数也会增加；但当TAM带宽增加到某一特定值时，测试时间不再改变，表明此时测试时间不再受TAM带宽影响，而是受TSV数影响。

以图12中Wmax=120时，多塔三维SoC2测试时间随L.TSVmax变化的趋势为例。在Wmax为120的条件下，当横坐标L.TSVmax小于100时，纵坐标上测试时间在减少；当L.TSVmax达到100时，测试时间保持不变。其原因为当给定TAM带宽值时，测试时间会随TSV数的增加而减少，这是由于增大TSV数，可供测试的资源量也随之增加；但当TSV数增加到某一特定值时，测试时间不再改变，表明此时测试时间不再受TSV数影响，而是受TAM带宽影响。

同样，以L.TSVmax=80为例，当Wmax分别为60,80和100时，测试时间呈下降趋势，但当Wmax大于100后，测试时间便不再变化。其原因是当给定TSV数时，测试时间会随测试引脚数的增加而减少，这是因为增加测试引脚数后，并行测试通道数增多；但当测试引脚数增加到某一特定值时，测试时间不再改变，表明此时测试时间不再受测试引脚数影响，而是受TSV数影响。

总而言之，当Wmax保持不变时，测试时间不会随L.TSVmax的增加一直减少；同样，当给定L.TSVmax值时，测试时间也不会随Wmax的增加一直减少，说明达到了“帕累托点”，因此，Wmax和L.TSVmax共同影响多塔三维SoC测试时间。另外，对于多塔三维SoC测试时间优化，增加测试引脚数比增加TSV数更有效。

5.2 同时考虑3种约束

本节实验是为了比较在Wmax和L.TSVmax值不变的情况下，改变Pmax的值后，本文算法相比量子粒子群优化QPSO(Quantum-Behaved Particle Swarm Optimization)算法的优越性。表6为同时考虑TAM带宽、TSV数和测试功耗约束时，本文算法与文献[12]的QPSO算法在多塔三维SoC1和多塔三维SoC2上的测试时间比较。第1、2、3列的Pmax、Wmax和L.TSVmax分别表示测试功耗、引脚数和TSV数上限；第4、5列分别为本文算法与QPSO算法在多塔三维SoC1和多塔三维SoC2上的测试时间比较情况，其中第3小列表示本文算法相比QPSO算法在测试时间方面减少的百分比。

Table 6 Comparison of TT on multi-tower 3D SoCs under constraints of Pmax表6 功耗约束下2种多塔三维SoC上测试时间比较

根据表6，设置Wmax=120，L.TSVmax=80时，本文算法与QPSO算法在多塔三维SoC1和多塔三维SoC2上随Pmax变化的测试时间TT比较，分别如图13和图14所示。

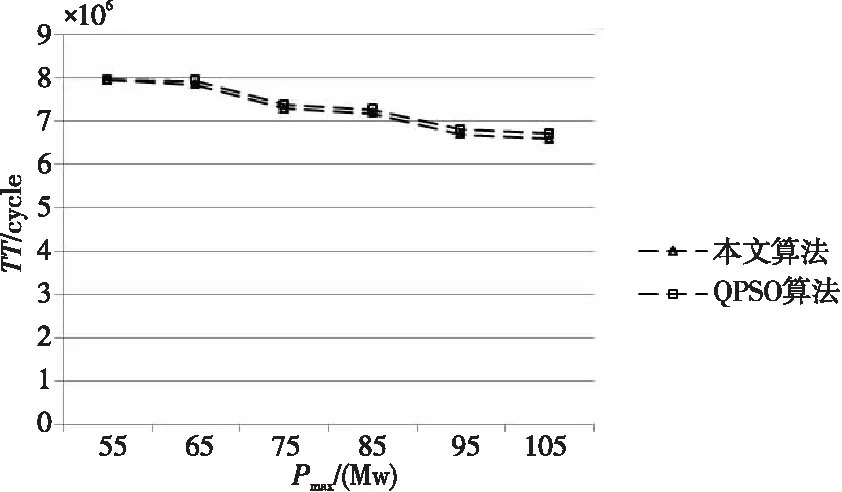
Figure 13 Comparison of TT of multi-tower 3D SoC1 under different Pmax when Wmax=120,L.TSVmax=80图13 Wmax=120,L.TSVmax=80时 不同Pmax下的多塔三维SoC1测试时间比较

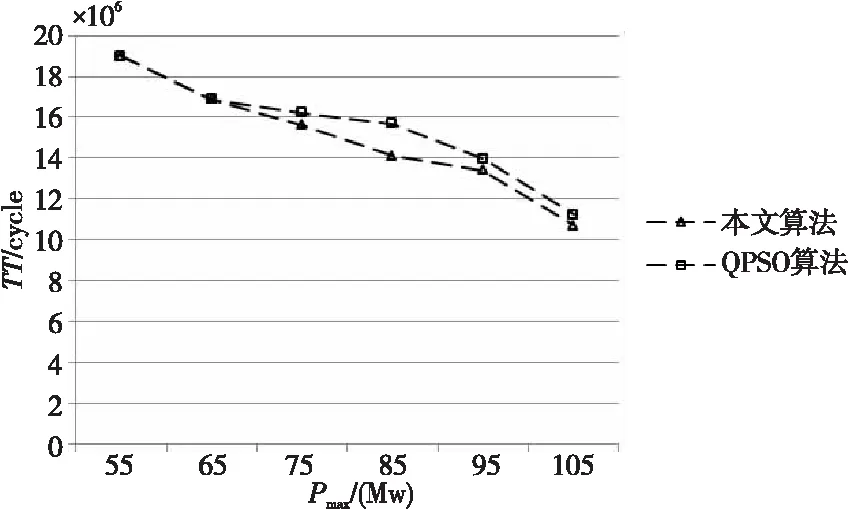
Figure 14 Comparison of TT of multi-tower 3D SoC2 under different Pmax when Wmax=120,L.TSVmax=80图14 Wmax=120,L.TSVmax=80时 不同Pmax下的多塔三维SoC2测试时间比较

由此得出，无论是对于多塔三维SoC1还是针对多塔三维SoC2，在Wmax，L.TSVmax，Pmax的取值分别与文献[12]中的QPSO算法取值相同时，本文算法所得到的总测试时间都更优。

6 结束语

针对多塔三维SoC测试时间长的问题，本文提出一种新型测试时间优化算法。该算法主要研究由测试架构已经固定的硬晶片构成的多塔三维SoC。首先将所有未测试晶片按测试时间降序排列。然后在排列中依次选择晶片测试时要遵循自底向上的原则。同时考虑Wmax、L.TSVmax和Pmax3种资源约束，每测试一个晶片，就计算剩余测试资源和测试结束时间，并标记为已测试。同时再把剩余未测试晶片降序排列后，按照晶片测试原则来选择晶片测试。直到剩余测试资源不满足待调度晶片测试时，释放第1个最早结束测试的晶片测试资源，再判断剩余测试资源是否满足待测试晶片。若满足，则调度晶片提前进入测试阶段，与未结束测试晶片实现部分流水，否则再释放第2个最早结束测试的晶片测试资源。以此类推，直至所有晶片测试完毕。在手工搭建的2种多塔三维SoC上运行本文算法，结果表明，与HA、TBT、LBL算法相比较，本文算法在多塔三维SoC1上的测试时间减少率分别高达20.34%,54.68%,58.96%；在多塔三维SoC2上的测试时间减少率分别高达27.78%,41.04%,68.87%。由该百分比数据得出，无论是在多塔三维SoC1上，还是针对多塔三维SoC2，本文算法都优于HA、TBT和LBL算法。因为本文算法通过释放最早结束测试的晶片测试资源，合理调度了待测试晶片的测试顺序，让待调度晶片提前进入测试阶段，减少了并行测试过程中的空闲时间块，从而使多塔三维SoC的TT明显减少。实验发现，增加测试引脚数比增加层间测试TSV数更能减少多塔三维SoC的测试时间。与HA、TBT和LBL算法相比，本文算法增加了测试功耗约束。与QPSO算法进行的实验对比分析表明，本文算法更具有优越性。