GROMACS 2020在ROCm平台上的移植与优化*

张驭洲，曹武迪，卜景德，谭光明，吉 青

(1.中国科学院理论物理研究所理论物理先进计算联合实验室，北京 100190； 2.中国科学院计算技术研究所计算机体系结构国家重点实验室， 北京 100190)

1 引言

分子动力学MD(Molecular Dynamics)[1]模拟是利用计算机模拟原子或分子运动的方法，通过模拟微观层面大量原子或分子的运动来研究物质的结构和性质。由于其可以方便地模拟实验方法难以测定的微观结构和物理过程而广泛应用于生物、化学、医药和材料等研究领域。经典MD模拟方法建立在牛顿力学基础之上，通过计算模拟体系中大量原子或分子之间的相互作用，最终得到整个体系的宏观统计信息。当前具有实际应用意义的MD模拟通常需要对包含至少数万、数十万粒子的体系进行百万乃至上亿时间步的模拟计算，在空间和时间尺度上都对计算能力有着极高的要求，因此，一直以来，MD都是高性能计算HPC(High Performance Computing)领域的一个重要应用方向。

GROMACS[2]是一个应用广泛的开源MD模拟软件。在众多的开源MD软件之中，GROMACS以高性能和高效率著称。当前世界上最大的分布式计算项目Folding@home[3]使用的计算引擎就是GROMACS。GROMACS拥有高度优化的CPU计算代码，支持通过MPI+OpenMP进行大规模并行计算，还通过CUDA支持NVIDIA GPU，并通过OpenCL支持其他加速设备，但OpenCL版本对新功能的支持一般落后于CUDA。当前最新的GROMACS 2020系列已经通过CUDA将MD模拟中计算量最大的3种作用力类型——短程非成键作用力、长程作用力和成键作用力均实现了GPU加速计算，性能得到了进一步提高[4]。而OpenCL版本目前尚不支持成键力在GPU上的计算。

ROCm(Radeon Open Compute)[5]是AMD推出的一个开源高性能异构计算平台，提供了包括GPU驱动、编译器、运行时、数学库、性能分析与调试工具在内的一整套编程开发和程序运行环境。ROCm提供了一个名为HIP(Heterogeneous-computing Interface for Portability)的编程模型及语言[6]，使用HIP编写的应用程序可以通过ROCm平台在AMD GPU上运行。HIP的应用层API与CUDA相似，可以较为方便地将现有CUDA程序转码为HIP程序，从而将只能在NVIDIA GPU上运行的应用移植到AMD GPU上。根据媒体披露，美国的3台E级高性能计算机中，有2台都将采用AMD GPU。

作为开源平台，ROCm拥有比闭源的CUDA更好的灵活性，但其生态的建设离不开丰富的应用的支持。本文通过将最新的GROMACS 2020系列转码为HIP代码，实现了向ROCm平台的移植，并通过对代码的一系列优化，在目标算例上获得了相对初始转码版本约2.8倍的加速比。据我们所知，这是目前世界范围内第一个实现最新版GROMACS完整功能的HIP版本。

本文主要有以下贡献：

(1)在ROCm平台首次实现了GROMACS 2020系列的完整功能，一方面为ROCm平台的生态系统添加了GROMACS这一应用广泛的HPC软件，另一方面移植的过程也可为其他应用的移植提供参考。

(2)以有代表性的算例为目标，在单结点内分析了其计算热点与瓶颈，进行了针对性的性能优化，获得了相对初始转码版本约2.8倍的加速比，其优化思路与方法也可以为其他GPU应用的优化工作提供借鉴；通过多结点扩展性测试，分析了扩展性方面的瓶颈，为后续优化打下了基础。

2 程序移植

HIP是ROCm 运行时环境之上的一层很薄的封装，它提供了一系列代码自动检查与转换工具，可以自动检查源文件中的CUDA API并转换为相应的HIP API，因此简单程序的移植已经十分方便。然而，大型的应用程序文件数量多，结构复杂，不仅代码文件需要转换，编译构建工具也需要修改，因此往往需要更多人工调试才能成功移植。

GROMACS经历了二十多年的不断开发与迭代，现在已经成为了一个庞大而复杂的应用软件，代码量已达百万行量级[2]。GROMACS 2020.2版本源代码基本组织结构如图1所示。主要的源码文件都位于src/gromacs目录下。GROMACS使用CMake[7]进行编译构建，顶层目录的cmake目录下是配置各种编译参数的cmake文件，在各级源码目录下都包括一个CMakeLists.txt文件，用于管理本级目录下源码文件的编译。通过使用HIP提供的工具完成自动代码转换之后，本文对代码和构建系统进行了调试修改，完成了编译，构建的GROMACS可以通过所有自带的单元测试。

Figure 1 Source code organization of GROMACS 2020.2图1 GROMACS 2020.2 源代码基本组织结构

3 性能优化

3.1 测试算例与基准

为保持与先前工作的一致性[8]，本文使用的算例是 [C16MP]+[Br3]-。首先验证HIP版GROMACS的计算正确性，然后作为性能基准，进行后续的代码优化。该算例模拟体系为离子液体体系，由1 440对离子构成，原子数为95 040，有大量成键相互作用(bonded interaction)和非成键相互作用nb(non-bonded interaction)。测试使用的软硬件版本及型号列于表1。分别使用GROMACS 2020.2原版CPU程序、原版OpenCL程序和本文移植的HIP版本程序，采用相同的模拟参数(版本功能特性相关参数除外)将测试算例运行5万时间步，运行的命令行参数列于表2。以原版CPU程序5万步平均计算结果为基准，OpenCL版和HIP版的相对误差结果都在同一数量级，并且都在MD允许的波动范围内，证明了HIP版计算结果的正确性；最后1万步统计的性能数据如表3所示。

Table 1 Software hardware and versions and models used in the test表1 本文测试使用的软硬件版本及型号

Table 2 Command line parameters used in the test表2 测试中使用的命令行参数

Table 3 Performance comparison of three versions of GROMACS on 10 000 steps running表3 3个版本GROMACS运行10 000步的性能数据

可见原版的OpenCL版本比CPU版本约有67.9%的加速，而移植的HIP版本性能甚至略低于CPU版本。

3.2 性能分析与瓶颈定位

MD的计算量主要来源于粒子之间的短程非成键相互作用(short-ranged non-bonded interaction)、长程相互作用(通过PME(Particle-Mesh-Ewald)方法计算)和成键相互作用。本文移植的HIP版GROMACS已经将这3种作用力的计算全部都在GPU上实现了，因此，需要一个GPU核函数性能分析工具来考察程序的性能瓶颈。ROCm提供了rocprof[9]工具来完成这一工作。rocprof可以在runtime层抓取GPU的运行数据，获得包括核函数的发起与结束时间、内存拷贝的起始、结束以及数据量等信息，还可以结合Chrome浏览器的tracing工具实现可视化。

Figure 2 Time lines of kernel of the first ported HIP code图2 HIP初始版本的核函数时间线

图2为HIP初始版本的核函数时间线。图2中显示的核函数执行顺序与GROMACS计算流程一致，但是每个函数的执行时间都异常长，因此本文后续着重对每个核函数进行了优化。

3.3 优化方法与结果

3.3.1 bonded核函数优化

bonded核函数是一个函数模板，在一个50时间步的运行中，其不同的实例调用次数、平均运行时间及总时间如表4所示。

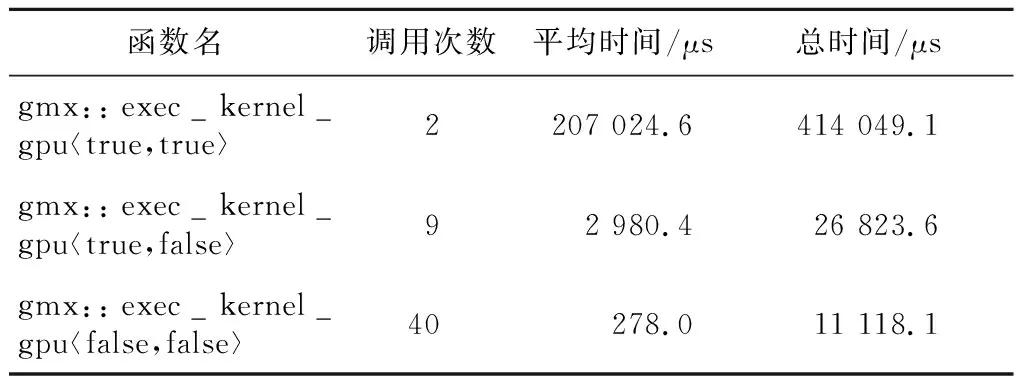
Table 4 Performance analysis results of the bonded kernel表4 bonded 核函数性能分析结果

不同的模板参数下，bonded核函数的运行时间差异较大。考察其代码，发现不同模板参数的实例的差异主要在于是否计算位力(virial，作用于粒子上的合力与粒子矢径的标积)和能量。位力和能量的计算需要将体系中所有粒子的贡献都累加起来，GROMACS原版的CUDA代码直接使用atomicAdd函数将每个线程的计算结果累加到GPU全局内存中的变量，这一操作在MI50 GPU上导致了严重的性能下降。MI50 GPU硬件支持32位整型的原子加操作，但是浮点型原子加操作是通过一个CAS(Compare-And-Swap)循环实现的，性能较差，大量对全局内存地址的原子加操作会严重降低程序性能。针对这种情况，本文将bonded核函数中对位力和能量的归约进行了修改，首先在block内部利用共享内存进行归约，然后再使用原子加在block之间进行归约。利用共享内存上较快的原子加操作代替了大量直接操作全局内存地址的原子加操作，相关核函数性能有了大幅提升。

此外，本文还修改了bonded核函数的发起参数，将原来256线程的block尺寸缩减为64线程，性能得到了进一步提高。MD中成键力的计算量与非成键力相比要小很多，并且有较多逻辑判断，严格意义上并不适合GPU计算。GROMACS原版的CUDA代码中，bonded核函数有一个包括8种成键力的switch语句。当某些warp发生分支，整个block的计算都将被减慢。将block尺寸减小到ROCm平台上warp(wavefront)的尺寸，就完全消除了正常warp对发生分支的warp的等待，从而进一步缩短了bonded核函数的平均执行时间。

图3为两步优化前后bonded核函数的性能。由于原来原子加操作只有在计算位力和能量时才会执行，因此第1步减少原子加操作的优化大幅减少了模板参数为〈true,true〉的核函数实例的运行时间，而其他2种实例性能不变。通过减小block尺寸的进一步优化，bonded核函数的3种实例性能都得到大幅提升，其中后2种实例执行时间甚至降为0，是因为单个核函数的执行时间已经小于性能分析工具所能抓取的最小时间间隔。

Figure 3 Average execution time of bonded kernels before and after optimization图3 优化前后bonded核函数的平均执行时间

3.3.2 PME核函数优化

PME部分的2个主要核函数pme_solve_kernel和pme_spline_and_spread_kernel中也使用了直接操作GPU全局内存的浮点型原子加操作，本文也对这2个函数进行了优化尝试。

(1)pme_solve_kernel。

当需要计算位力和能量时，pme_solve_kernel核函数的每个线程需要计算6个位力分量和1个能量变量，这7个量需要全局累加。原版代码首先使用shuffle指令和共享内存，将每个线程所计算的7个变量的结果归约到线程所属block的前7个线程，然后每个block的前7个线程使用浮点型原子加操作将结果归约到全局内存。尽管已经通过shuffle指令和共享内存归约了block内的结果，但由于block数量众多，所有的block都对全局内存中同样7个地址进行原子加操作，仍然严重影响了性能。

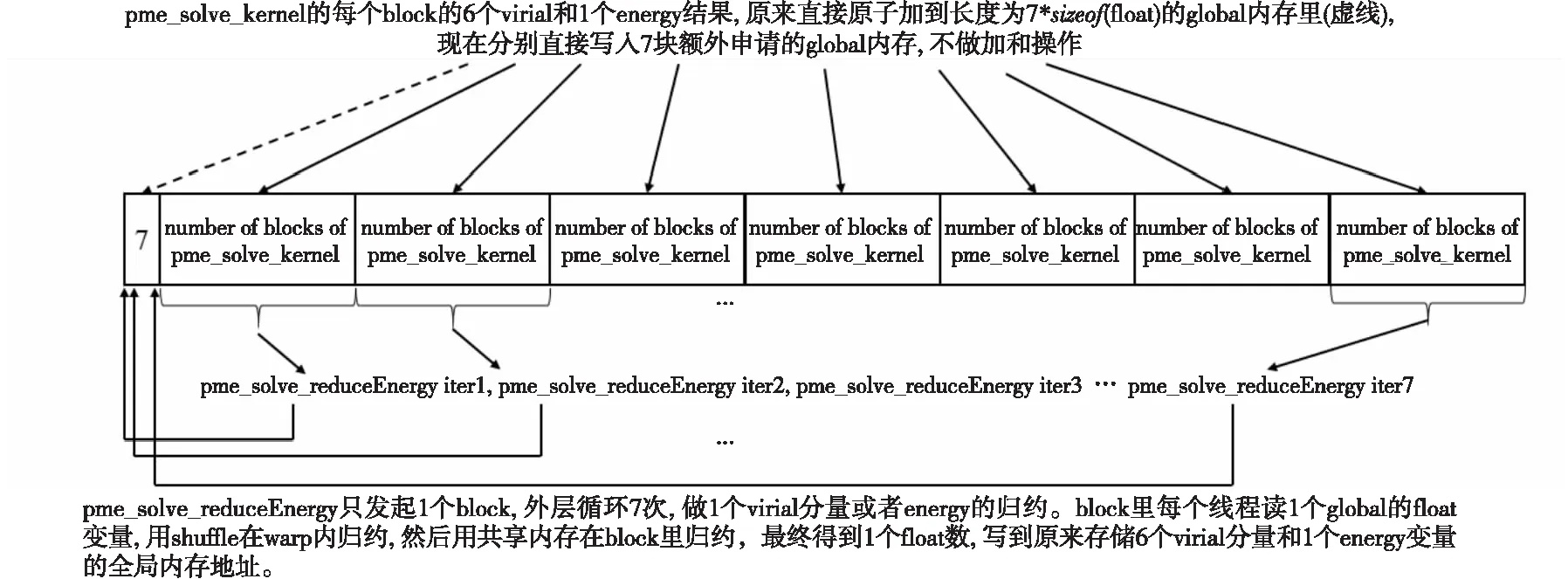
Figure 4 Schematic diagram of pme_solve_kernel optimization 图4 pme_solve_kernel优化示意图

为了避免使用性能不佳的原子加操作，本文在原来保存7个位力和能量变量的GPU全局内存地址之后再额外申请一段内存，其长度为pme_solve核函数的block数乘以7个float变量大小。pme_solve_kernel在计算得到7个位力和能量变量之后不再向全局内存归约，而是直接写入额外申请的全局内存中，按照分量的种类写入其对应的内存块，每种分量数量等于pme_solve_kernel的block数，总共7种分量。在全部的pme_solve_kernel核函数完成计算和全局内存写入之后，使用另外一个单独的核函数读取pme_solve_kernel核函数写入全局内存的结果，使用shuffle指令和共享内存进行block内的归约。该单独归约的核函数的block尺寸设置为MI50 GPU允许的最大blockSize 1 024，并且只发起一个block，这样block内的归约结果就是最终结果，从而完全避免了对全局内存原子加操作的使用。图4为pme_solve_kernel优化示意图。

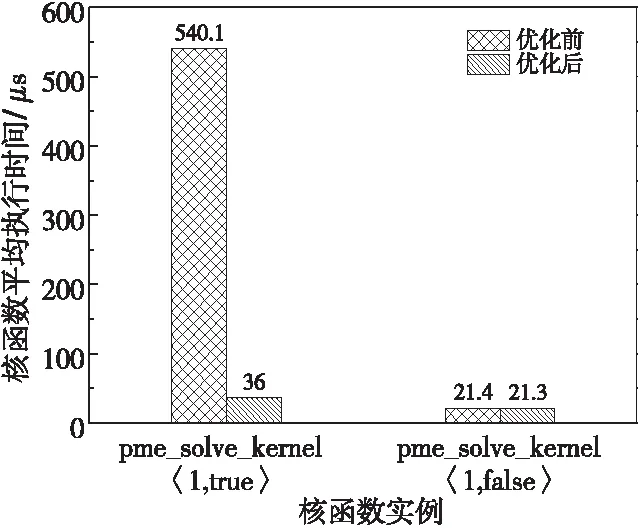
Figure 5 Average execution time of the pme_solve_kernel before and after optimization图5 pme_solve_kernel核函数 优化前后核函数平均执行时间

图5为优化前后pme_solve_kernel不同实例的平均执行时间。可见对原子加操作的优化大幅提升了计算位力和能量的核函数实例的性能，其执行时间已经接近不计算位力和能量的核函数实例。当然，为了替代原子加，本文引入单独归约核函数，该核函数平均执行时间约15 μs，因此总体上仍然提升了代码性能。

(2)pme_spline_and_spread_kernel。

pme_spline_and_spread_kernel核函数的一个功能是将每个粒子的电荷分散到周围n3个FFT(Fast Fourier Transform)网格点上，n为B样条插值的阶数。该操作在block内的原子加操作写入同一全局内存地址的比例很少，而不同的block之间则有较多访问同一全局内存地址的原子加操作，因此无法通过先行归约block内的线程来减少原子加操作的数量。而对于在pme_solve_kernel中使用的方法，即通过单独的归约核函数来避免原子加操作，这里也不再有效。这是因为，从归约的目标地址和每个目标地址上所需归约的元素的数量来看，pme_solve_kernel的原子加操作是“密集型”：归约目标为7个全局内存地址，每个地址需要累加至少上千个元素；而pme_spline_and_spread_kernel的原子加操作是“稀疏型”：归约目标为整个体系FFT网格的所有格点，每个格点需要累加的元素数目不定，而是根据该点周围的带电粒子密度而变化的，一般多则几十个，少的甚至为零，而FFT网格的数目却很大，以本算例为例，FFT网格尺寸为72 × 48 × 192，共663 552个格点。pme_solve_kernel采用的单独归约核函数方法，在这种情况下将变得极为低效：首先，需要额外申请的内存空间很大，对于本例来说，即使假设每个目标地址最多只需要累加10个元素，总共也需要6 635 520个float数，超过25 MB的全局内存；而且由于每个时间步每个目标地址所需累加的元素个数可能改变，每一步计算都需要将这些内存全部清零。其次，对于这样大量的数据，采用单独的归约核函数从全局内存读入再归约，也非常耗时。本文实现了该方法并进行了测试，结果表明，在pme_spline_and_spread_kernel核函数中使用单独的归约核函数后，性能比原来直接使用原子加更差。因此，本文对于该核函数没有进行进一步的优化，仍然使用原版直接原子加操作的方案。这一案例也体现了从硬件上直接加速原子加操作的必要性。

3.3.3 nb核函数优化

短程非成键相互作用(nb)是MD中计算量最大的部分，并且非常适合GPU计算，因此也是GROMACS最早实现GPU计算的部分。GROMACS为nb设计了一个精巧的算法[10]，在CPU和GPU上都获得了良好的性能。随着GROMACS支持的模拟种类的不断丰富，nb核函数已经成为了一个包含数十种版本的函数模板。本文针对MI50 GPU的硬件特性，对[C16MP]+[Br3]-算例所使用的nb核函数实例代码进行了2个方面的优化，获得了一定的性能提升。

(1)减少原子加操作数量。

nb核函数同样使用了访问全局内存地址的浮点型原子加操作，分别用于归约每个粒子受到的邻居粒子的作用力和偏移力。原版CUDA代码中，对于大部分CUDA设备，nb核函数的每个block都是64线程(计算能力为3.7时为128线程)，占用2个warp，因此在归约时也是按照2个warp进行设计。在MI50 GPU上，nb核函数刚好只占用1个warp，因此我们把相关的归约均改为warp内的shuffle操作，将访问全局内存的浮点型原子加操作数量减少了一半，提高了该核函数的性能。

(2)减少寄存器使用量。

尽管GPU被设计为用于大规模的并行计算，但是其并行性也是受硬件资源数量限制的，主要的限制因素是核函数中共享内存以及寄存器文件的使用量。nb是一个规模较大的核函数，使用了较多的寄存器变量。本文将编译该核函数得到的目标文件反汇编后，发现其占用的寄存器数量达到97个，在ROCm平台，这一寄存器使用量导致MI50 GPU上的每个单指令多数据SIMD(Single Instruction Multiple Data)计算组只能并发执行2个warp。较低的并发数使得程序运行过程中某些指令(例如原子加操作)的延迟难以得到掩盖。

nb核函数虽然使用的寄存器数量较多，但共享内存的用量却相对较少，如能将部分寄存器变量转为使用共享内存，有望提高并发数。然而，共享内存的读写速率仍然是远低于寄存器变量的，实际验证中发现，在循环中有写操作的寄存器变量转移到共享内存后核函数性能反而下降。经过对代码的分析发现，nb_sci是一个包含4个int分量的结构体变量，它在所有循环开始之前赋值1次，后续的循环之中只有读操作，没有写操作。将nb_sci变量转移到共享内存之后，nb核函数寄存器使用量降低为81个，这样SIMD并发的warp数增长为3，经过实际测试，执行次数占绝对多数的nb核函数实例nbnxn_kernel_ElecEw_VdwLJCombLB_F_cuda性能有约7%的提升，因此，在另外2个nb核函数性能基本不变甚至略有下降的情况下，程序的总体性能仍有提升。图6为优化前后nb核函数实例的平均执行时间。

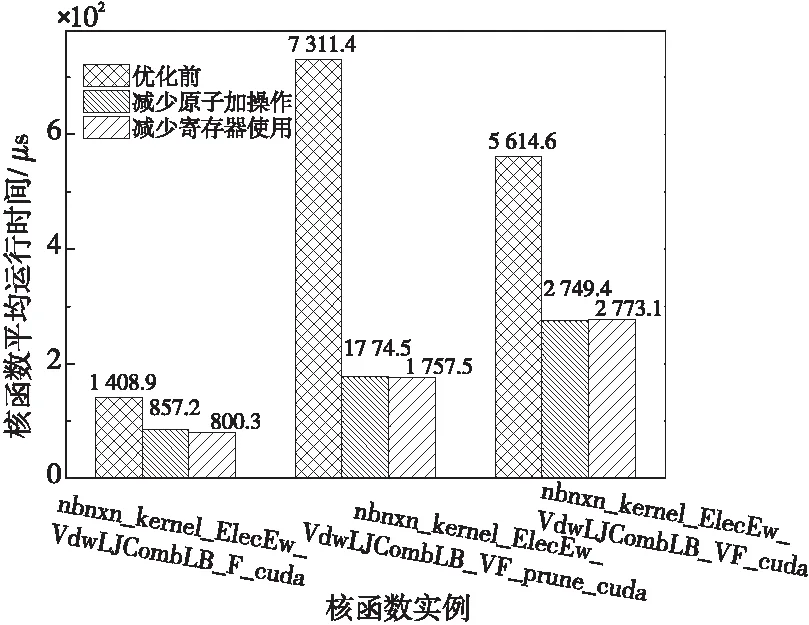
Figure 6 Average execution time of the nb kernels before and after optimization图6 优化前后nb核函数的平均执行时间

3.4 其他算例性能测试

通过对MD模拟中计算量最大的3部分(即短程非成键相互作用、长程相互作用以及成键相互作用)的GPU核函数nb、PME和bonded的优化，[C16MP]+[Br3]-算例的性能从最初的13.109 ns/d增长为36.980 ns/d，提升182.1%。

表5列出了实施一系列优化措施后算例的整体运行时间，时间统计方法与表3数据统计方法一致，并计算了各个版本以无优化HIP版本为基准的加速比。为进行对比，表5中也加入了表3中CPU和OpenCL程序的运行时间。可见经过优化之后，HIP版本性能已经超过原版CPU和OpenCL版本的。

为验证优化的通用性，本文还对另外2个典型算例——Lysozyme[11]和waterbox[12]进行了性能对比测试。Lysozyme是对水盒子中的溶菌酶蛋白质的模拟，体系原子数为71 844，相对[C16MP]+[Br3]-，其成键力计算要少得多。waterbox是仅包含溶剂水分子的体系，本文使用的是包含64万个水分子、共192 000个原子的体系，规模较大，但是成键力全部以“约束”(constraint)的方式在CPU上计算。表6列出了Lysozyme和waterbox算例的运行性能数据，可见优化的HIP版本相对优化之前以及原版的CPU和OpenCL版本均有一定的性能提升。

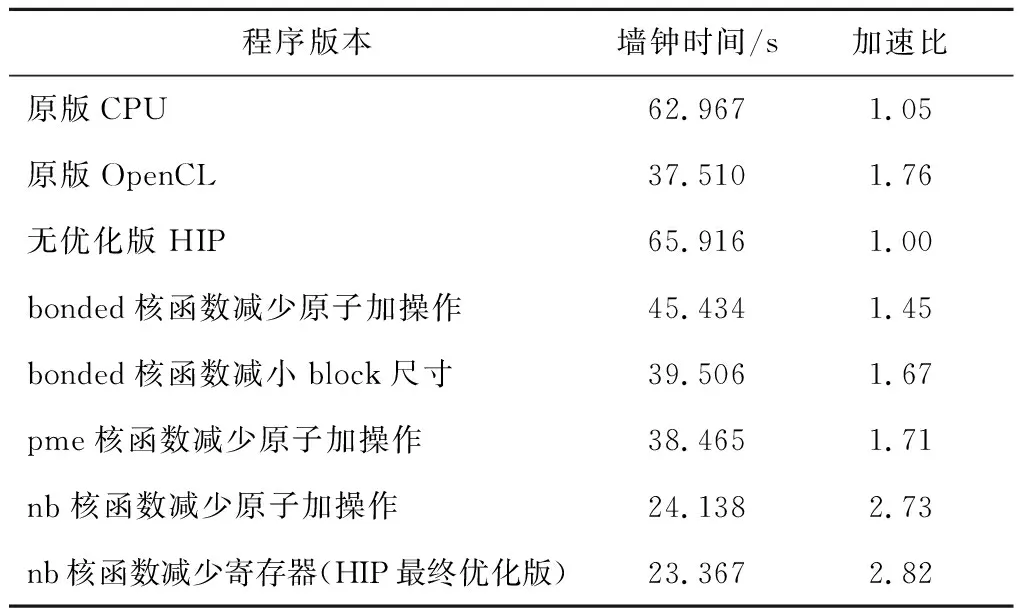
Table 5 Performance comparison among different optimization methods表5 不同优化方法性能对比

Table 6 Performance comparison among different GROMACS versions with Lysozyme and waterbox benchmarks表6 算例Lysozyme和waterbox在不同版本GROMACS下的性能对比

进一步对比这2个算例的性能数据，运行Lysozyme算例时OpenCL版比CPU版的性能高71.6%，而运行waterbox算例时OpenCL版比CPU版的性能高97.4%，可见GROMACS作为一个通用MD模拟软件，支持的模拟种类众多，由于不同类型的算例实际运行的代码不同，即使是官方原版，计算不同算例的相对性能也有差异。本文以[C16MP]+[Br3]-这一算例为目标进行的一系列优化，对Lysozyme和waterbox算例也有一定加速效果，证明了优化措施的通用性；但另一方面，在Lysozyme和waterbox算例上的加速效果不如[C16MP]+[Br3]-，这也体现了通用代码的复杂性。若要获得最佳的性能，则需要对目标算例进行针对性的分析与优化。

3.5 扩展性测试

为了从更多角度测评优化效果，本文还使用优化前后的HIP代码分别进行了扩展性测试，包括弱扩展性测试和强扩展性测试。由于PME算法本身在计算过程中要求全局通信，因此GROMACS 2020版本只支持单GPU卡计算PME，即使使用多结点运行，也只能指定使用一个进程单独计算PME，通常这会对程序的扩展性造成不利影响。使用CPU计算PME则没有这一限制，因此，在扩展性测试部分，各个规模下均使用CPU计算PME，bonded和nb部分仍然使用GPU进行计算。

弱扩展性测试将[C16MP]+[Br3]-这一算例规模分别扩展为原来的1倍、2倍、4倍和8倍，分别使用1,2,4和8个结点进行计算。强扩展性测试则将[C16MP]+[Br3]-这一算例扩展为原来的8倍，分别使用1，2，4和8个结点进行计算。扩展性测试中时间统计方法与表3数据统计方法一致，结果分别列于表7和表8。

Table 7 Test results of weak scalability 表7 弱扩展性测试结果

Table 8 Test results of strong scalability 表8 强扩展性测试结果

由于PME部分采用CPU计算，所以损失了该部分的优化效果，但在2种扩展性测试中，各个测试规模下优化后的HIP版本均比优化前有明显的性能提升。同时也可以发现，优化后相比优化前的加速比不及单结点时的情况。其主要原因是该算例PME部分计算量较多，使用CPU计算PME时该部分运行时间在总时间中占比始终过半，同时随着结点数和算例规模的增加，PME部分通信量也迅速增加，对性能的制约更加严重，因此优化效果逐渐降低。

图7a和图7b分别展示了弱扩展性和强扩展性测试中不同规模下优化前后算例运行总时间和PME时间，可见优化前后，随着结点数的增长，PME部分时间占比都是增长趋势，且优化后，各个规模下PME时间占比都超过65%，说明PME以外的部分都得到了较好的优化。

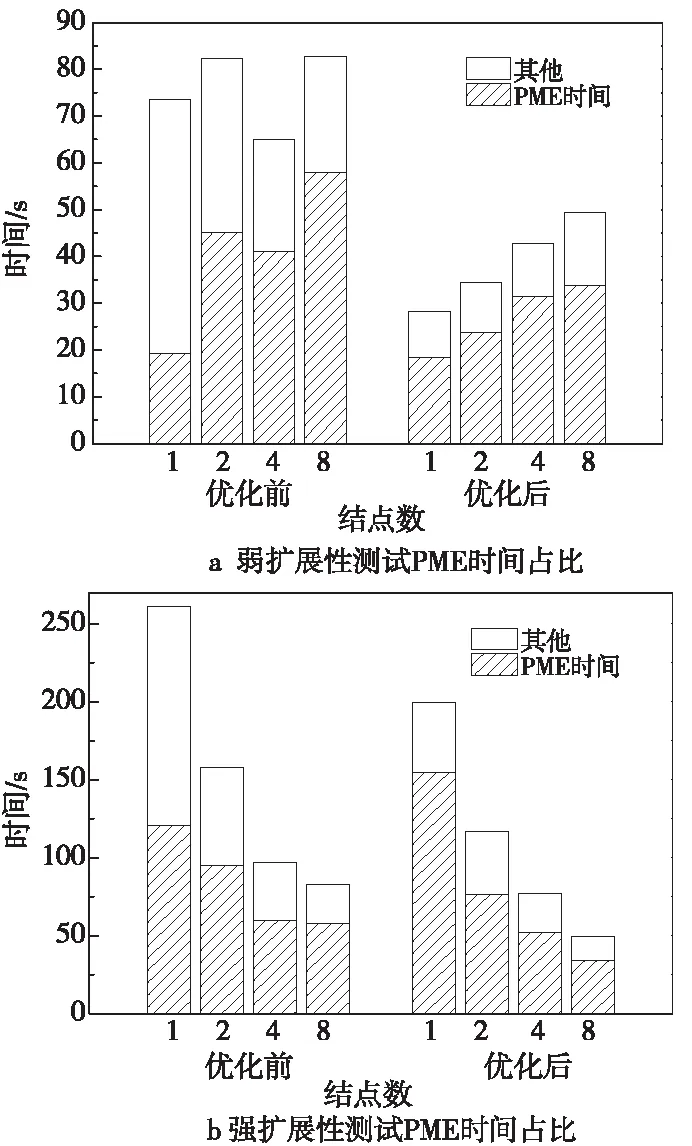
Figure 7 Percentage of PME time in scalability tests 图7 扩展性测试PME时间占比

扩展性测试的结果表明，尽管本文并未针对GROMACS的通信以及计算流程等方面进行优化，但通过对GPU核函数的优化，在多结点计算时相对优化前仍取得了可观的性能提升。另一方面，该组测试也体现了PME部分对扩展性的限制，为后续针对多结点、大规模计算的优化指明了方向。

4 结束语

本文通过将广泛使用的分子动力学模拟软件GROMACS 2020系列转码为HIP代码，实现了其功能在ROCm上的完整移植。进一步以一个复杂的离子液体模拟算例为目标，对其主要GPU核函数进行了逐一优化，实现了相对初始转码版本约2.8倍的加速比。优化后的版本在MI50 GPU上的性能高于GROMACS原版OpenCL代码60.5%，相对运行在EPYC 7502 处理器的原版CPU代码的加速比约为2.7。此外，本文还在另外2个典型算例Lysozyme和waterbox上进行了测试。结果显示，优化后的HIP版本相对原版CPU和OpenCL版本均有一定的性能加速。通过对所用离子液体算例的扩展，分别测试了优化前后HIP版本代码的强弱扩展性，一方面说明针对单结点的优化在多结点运行时仍然体现了良好的加速效果，另一方面也发现了PME部分对扩展性提升的制约，为后续针对大规模体系的优化提供了方向。本文的工作丰富了GROMACS可使用的软硬件平台，所采用的移植方法、优化思路及方法对于其他GPU应用的移植和优化也有一定借鉴意义。未来我们将就更大规模的可扩展性优化展开研究。