一种波纹管蛇形机器人的结构设计及运动分析

唐 军，杨书麟，秦 智

（江西理工大学机电工程学院，江西 赣州 341000）

1 引言

仿生机器人能代替人类完成特定的任务，如探矿、深潜、维修、辐射区救援，目前仿生机器人主要有：多足机器人、跳跃机器人、仿鸟机器人、仿鱼机器人、水下机器人等[1-2]。但对于空间狭小、地形复杂的环境，常规的仿生机器人难以胜任，因此研制一款灵活性高、运动形式多样的机器人[3-4]势在必行。

文献[5]研制的ACM系列蛇形机器人采用串联或正交串联的连接方式，可以完成多维运动，但结构复杂，运动受限；文献[6]研制的S系列蛇形机器人，各机器人的关节尺寸不同，提高了对环境的适应性。国内沈阳自动化研究所研制的巡视者Ⅱ蛇形机器人可完成俯仰等三维运动，其关节采用万向连接且装有被动轮，致使结构复杂[7]；除此之外，文献[8-10]研制出了装有单、双向被动轮及蛇形机器人，文献[11]研制出了一种桥梁缆索攀爬蛇形机器人[11]，文献[12]研制了一种叶片轮式救援蛇形机器人。以上仿生机器人的结构大多数都具有主动轮或被动轮，使得蛇体结构变得复杂，在复杂的环境下不能完成指定运动。另外，许多蛇形机器人各蛇关节部件都裸露在外，在外界恶劣的路面环境下，蛇形机器人运动时难免与地面接触造成磨损损失，缩短了蛇形机器人的使用寿命。针对以上问题，本文设计了一种波纹管蛇形机器人，利用波纹管替换主、被动轮使其结构简单，同时波纹管包裹住蛇形机器人，使其成为一个“柔性”整体，使得蛇形机器人结构更紧凑，适应性更强。并且波纹管包裹住蛇形机器人使其避免与地面直接接触，降低了蛇形机器人的磨损，提高了蛇形机器人的使用寿命。

2 蛇形机器人的结构设计

2.1 蛇形机器人内部关节设计

生物蛇是一种无肢动物，且没有胸骨，它的肋骨可以前后自由移动，肋骨与腹鳞之间有肋皮肌相连，当肋皮肌收缩时，肋骨便向前移动，所以对于蛇形机器人来说，内部关节设计是十分重要的。单个蛇关机模型，如图1所示，它是由舵机、支架1、支架2和舵盘组成。并且支架通过舵盘与舵机相连接，可自由旋转。蛇关节长度为74.74 mm，支架1 的长度为70 mm，支架2 的长度为50 mm。在工作时，可通过水平方向和垂直方向的角度变化的时差以及水平与垂直方向的步距变化，来实现蛇形机器人的各种运动。蛇头关节模型，如图2所示。在蛇头关节模块前端装有摄像头，用来记录分析路况信息。

图1 单个蛇关节Fig.1 Single Snake Joint

图2 蛇头关节Fig.2 Snake Head Joint

2.2 蛇形机器人的蛇体设计

蛇形机器人通常有平行连接、P－R连接、万向节连接以及正交连接等关节连接方式。而正交连接相比较其他几种方式来说，结构更简单直观，控制也相对容易。所以文中设计的蛇形机器人采用了前后关节互为正交连接的关节连接方式。同时为了简化结构并使其结构更为紧凑，本文利用波纹管代替了主、被动轮结构，并包裹住蛇体。蛇形机器人三维模型，如图3所示。它是由8个蛇关节通过正交串联的方式连接并嵌套在波纹管内，每个蛇关节有2个自由度，整体共有16个自由度。其总体尺寸为710*72*72 mm。波纹管则选用质量小、弹性好的单层塑料波纹管。在舵机选择方面，为了突出轻量化和精密化等特点，这里选用RDS3115数字舵机。该舵机运行噪音低、平稳且线性度高，特别适合机器人的各关节活动。单个舵机重量为60 g，工作电压为（6～7.4）V，堵扭转矩为15 kg·cm－16 V，17 kg·cm－17.4 V，可控角度范围270°，断电可360°旋转。

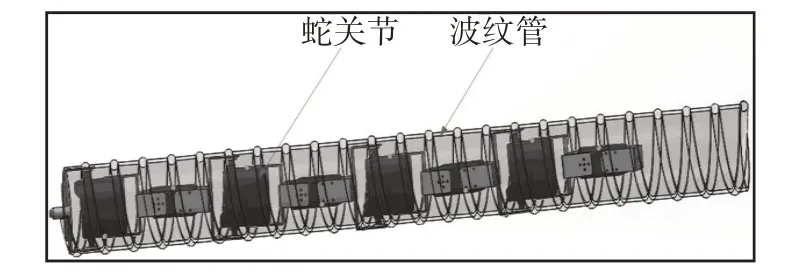
图3 蛇体三维模型Fig.3 Three－Dimensional Snake Body Model

3 蛇形机器人的数学模型

3.1 蛇形机器人的运动学模型

设计的蛇形机器人是由8个的蛇关节通过正交串联组成的，为了简化模型，这里只对相邻的2个蛇关节模块进行D－H坐标系建立与分析，并求出其齐次变换矩阵。相邻D－H坐标系，如图4所示。

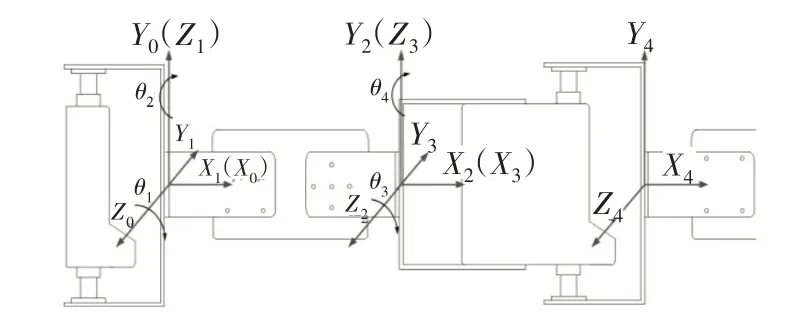
图4 相邻关节D－H坐标系Fig.4 D－H Coordinate System of Adjacent Joints

各运动参数，如表1所示。

表1 相邻关节D－H坐标参数Tab.1 D－H Coordinate Parameters of Adjacent Joints

表中i—坐标编号；θi—绕z轴的旋转角；di—关节偏移；ai—连杆长度；αi——扭角。

将各参数带入齐次变换矩阵（1）：

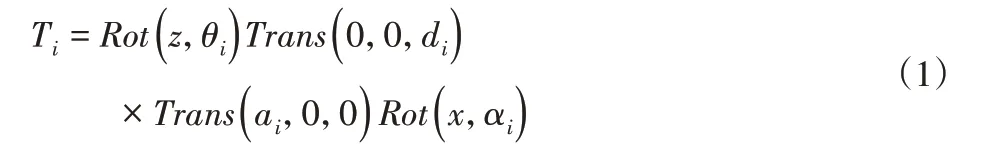
故可得：

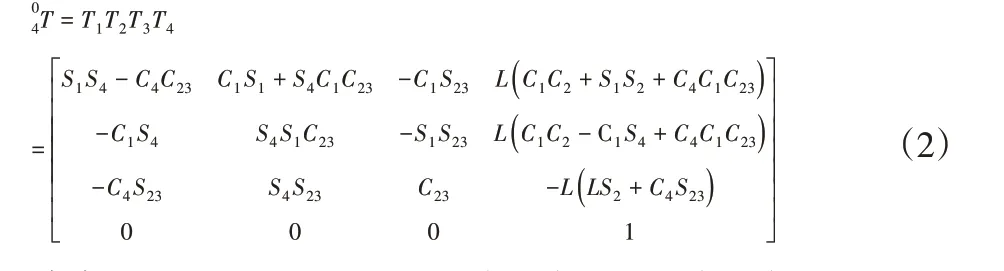
式中：Si=sinθi；Ci=cosθi；Sij=sin（θi+θj）；Cij=cos（θi+θj）。

3.2 蛇形机器人的动力学模型

蛇形机器人简化模型，如图5所示。以蜿蜒运动为例可以把整个蛇形机器人简化成由N个杆件串联而成的杆组，并对其进行受力分析。

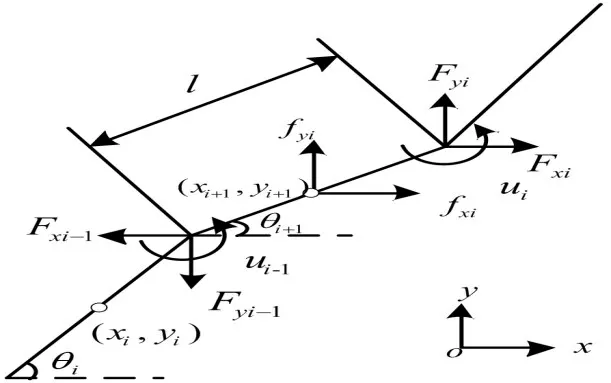
图5 蛇形机器人简化模型Fig.5 Simplified Model of Snake-Like Robot

且相邻连杆必须满足以下两个完整的坐标约束，即

式中：l—单个杆件的长度；m—单个杆件的质量；（xi，yi）—第i个杆间的重心位置；θi—第i个杆件与x轴的夹角。

可通过矩阵形式求出各蛇关节的关节约束及蛇关节的全局位置坐标。即：

式中：X＝（x1，…，xN）；Y＝（y1，…，yN）表示连杆重心的全局坐标；

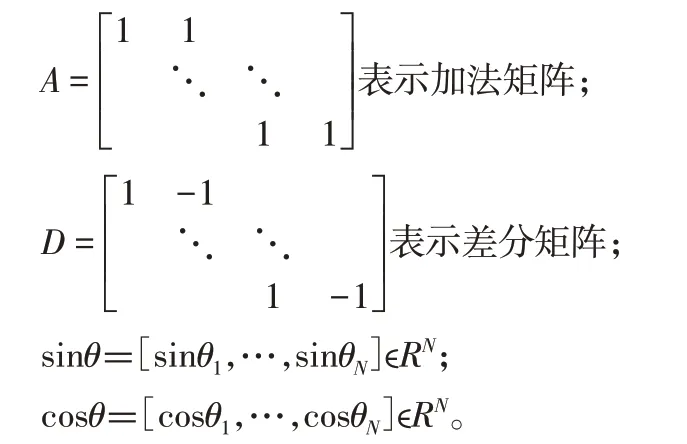
而蛇形机器人的全局坐标位置可表示为：

式中：e＝（1，…，1）∈RN。

故将各个连杆的位置表示为连杆角度的函数为：

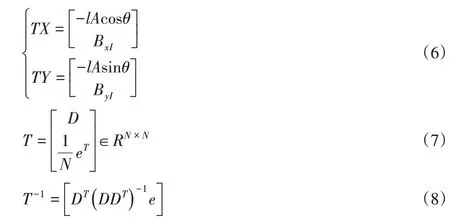
所以蛇关节的全局位置坐标为：

式中：K=AT(DDT)-1D∈RN×N

然后通过对蛇形机器人的各杆件受力分析可知蛇形机器人在运动时，不仅受到地面产生的摩擦力和摩擦力矩，而且相邻杆件互相也会产生作用力与力矩，故可得如下各杆件力与力矩方程：

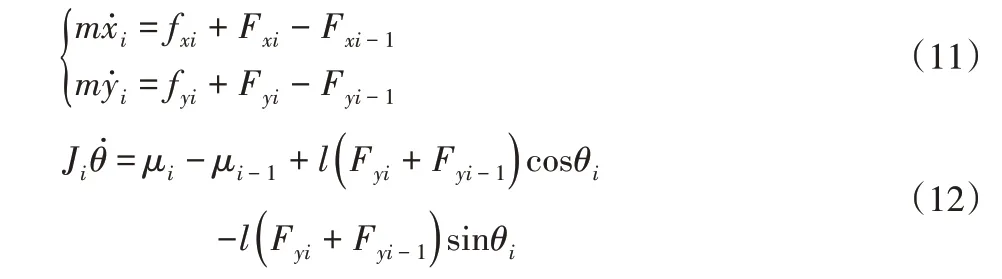
式中：fxi、fyi—第i个连杆所受到的地面摩擦力；Fxi、Fyi、Fxi-1、Fyi-1—相邻关节对连杆产生的作用力；μi、μi-1—舵机对连杆产生的力矩；Ji—连杆转动惯量。

4 蛇形机器人步态的实现

在生物界，蛇的骨骼结构较为特殊，其骨架由多节骨节相互串联而成，实现了身体的柔韧性与灵活性输出，完成各种形式的运动。这里设计的波纹管蛇形机器人可通过调节水平及垂直蛇关节的运动方式来实现各种运动。

4.1 蛇形蜿蜒运动

可以通过控制水平蛇关节在运动时保持直线不变，而通过控制垂直蛇关节的舵机，使其按照正弦规律运动来实现蜿蜒运动。其运动方程为：

4.2 伸缩运动

伸缩运动是使垂直的蛇关节在运动时保持直线不变，而通过控制水平蛇关节舵机，使其按照正弦规律运动来实现的。蛇正是依靠这种运动来通过某些复杂的空间。其运动方程为：

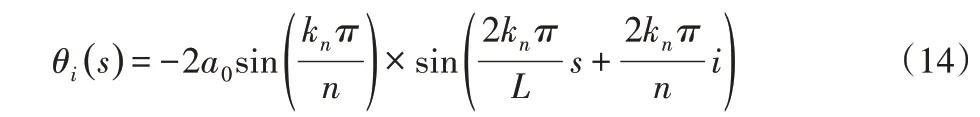
4.3 侧向运动

侧向运动是通过控制水平蛇关节和垂直关节的舵机都按照正弦规律运动来实现的。并且，水平蛇关节和垂直关节的运动曲线存在一个运动相位差。其运动方程为：

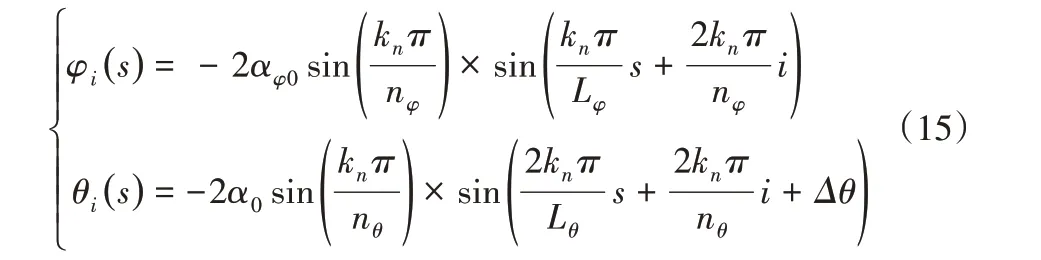
4.4 翻滚运动

翻滚运动则可通过改变各蛇关节的步距变化和运动角度时差来实现。其运动方程为：

式中：φ（is）、θi(s)—垂直和水平蛇关节舵机的转动角度；i—蛇关节的个数；α0—蛇形机器人的初始角度；s—蜿蜒曲线的长度；kn—蜿蜒曲线的个数；n—蛇关节的个数；Δθ—相位差；L—蛇形机器人的总长度。

5 ANSYS磨损仿真及分析

利用Solidworks 绘制出蛇形机器人的三维模型并导入到ANSYS 2019R1中对蛇形机器人进行磨损仿真，通过得到的磨损量曲线来分析蛇形机器人运动时的磨损情况。仿真选用Transient Structural模块，接触模型选为fricitional，摩擦系数为0.5，behavior 出定义为asymmetric，formulation 处选择Augmented lagrange，磨损系数为2，网格选用六面体网格。蛇形机器人在有无波纹管两种情况下的运动磨损量对比曲线，如图6所示。

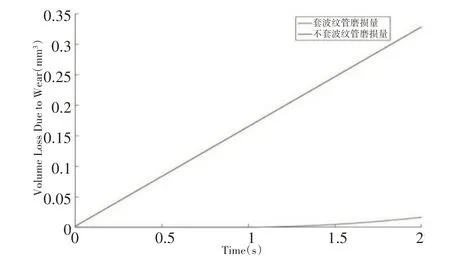
图6 蛇形机器人磨损量横向对比曲线Fig.6 Lateral Contrast Curve of Wear Amount of Serpentine Robot

当蛇形机器人不套波纹管运动时，会与地面接触而产生磨损，由图可知，运动了2s后其磨损量约为0.33mm3，且随着运动时间的增加，磨损量也随之增加。当蛇形机器人套上波纹管时，其不与地面直接接触，仅会通过蛇关节转轴带动支架转动而产生磨损，且运动1s 后磨损量接近于零，运动2s 后的磨损量约0.016mm3，仅为不套波纹管时蛇形机器人磨损量的二十分之一。

综上所述，蛇形机器人不套波纹管运动时所产生的磨损量远大于套了波纹管后所产生的磨损量，故波纹管包裹住蛇形机器人后避免了其运动时与地面直接接触，有效的减少了蛇形机器人在运动时产生的磨损量，进而提高了蛇形机器人的使用寿命。

6 Adams运动仿真及分析

先用三维制图软件Solidworks绘制出蛇形机器人的三维模型，然后将其另存为.x＿t的格式，再利用Adams仿真软件来进行仿真。此次仿真实验是通过蛇形蜿蜒运动为例来进行的，并根据所设计的蛇形机器人的大致条件来设定初始条件参数。其单元质量为0.50kg；模块数为8；驱动形式为舵机驱动。蛇体模型，如图7所示。蛇关节连接模型，如图8所示。本次仿真实验以蛇形机器人的整体为实验对象，通过研究转矩、速度、加速度和蛇体长度随时间的变化情况来分析该蛇形机器人的运动情况。

图7 蛇体模型Fig.7 Snake Body Model

图8 蛇关节连接模型Fig.8 Snake Joint Connection Model

转矩随时间的变化，如图9所示。在1.3 s左右，蛇形机器人的转矩达到最大值46.5 N·mm，并且在转矩拐点处过渡平滑，整个运动过程也并无瞬间增大或减小的冲击状态，故运动过程平稳。

图9 转矩随时间的变化Fig.9 Torque Change with Time

速度随时间的变化，如图10所示。该蛇形机器人的速度变化周期约为1.7 s，且能在1 s 内使速度达到最大值100 mm·s-1。同时在速度临界点处，即速度为零时，并无反向变化，故蛇关节间不会产生相互的冲击阻力，所以在完成整个蛇形蜿蜒运动时，其运动速度不会产生瞬波动。

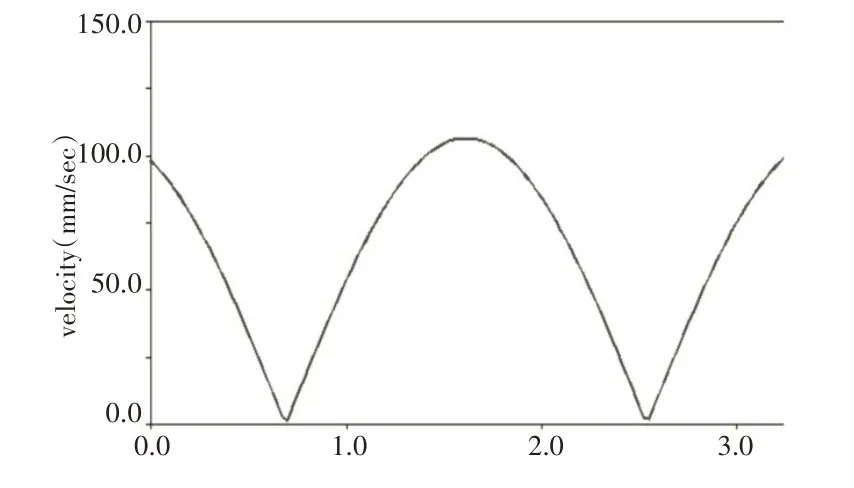
图10 速度随时间的变化Fig.10 Variation of Velocity with Time

加速度随时间的变化，如图11所示。其加速度呈正弦周期性变化，加速周期为2 s，且最大加速度177.5 mm·s-2，且整个过程过渡平稳，无加速度脉冲。

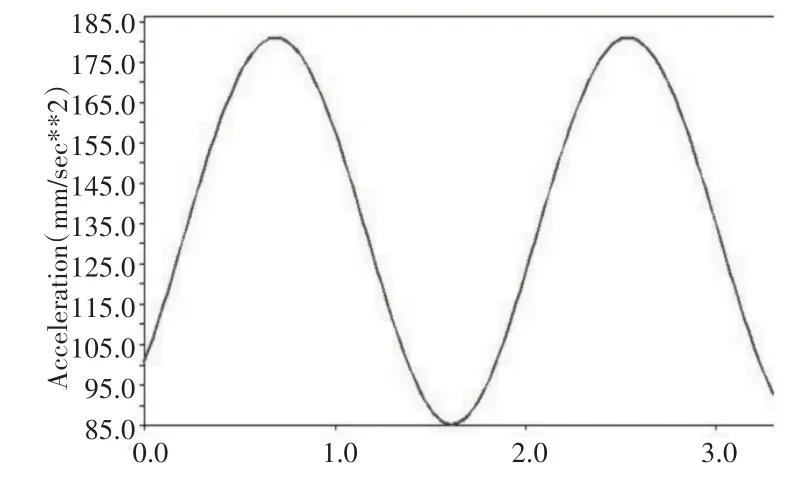
图11 加速度随时间的变化Fig.11 Variation of Acceleration with Time

蛇形机器人在做蜿蜒运动时蛇体长度随时间的变化，如图12所示。在运动时，蛇体最长约为398 mm，最短约为387 mm，且整个长度变化平稳，说明在运动时蛇体并无侧滑及停滞等不正常状态，运动效果较好。

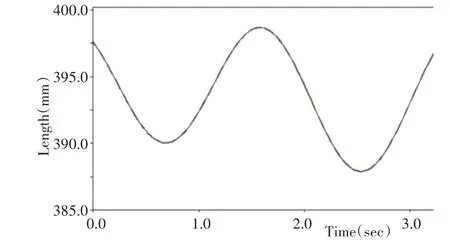
图12 蛇体长度随时间的变化Fig.12 Changes of Serpent Body Length with Time

7 结论

（1）利用波纹管来代替传统轮式蛇形机器人的主、被动轮，不仅简化了蛇形机器人的结构，而且还能够包裹住蛇形机器人，使其成为一个“柔性”整体，能适应更复杂的环境，同时也延长了各蛇关节部件的使用寿命。（2）通过solidworks对蛇形机器人进行结构设计，并构建了D-H坐标系对蛇形机器人进行运动学分析，求出齐次变换矩阵。然后通过改变蛇形机器人的各蛇关节的运动来实现其常规运动。同时并将蛇形机器人的结构简化成杆组，对其进行动力学建模，得出力及力矩方程。（3）通过ANSYS对蛇形机器人进行了磨损仿真分析，仿真结果表明波纹管避免了蛇形机器人运动时与地面直接接触，进而减少了蛇形机器人的磨损量，提高了蛇形机器人的使用寿命。同时以蛇形蜿蜒运动为例，利用Adams对该蛇形机器人进行了运动仿真，并且通过仿真结果可知该蛇形机器人速度、加速度过渡平稳，且速度无反向变化，在力矩峰值处也无冲击现象，蛇体长度也按周期性变化，运动过程平稳。