改进的野草入侵算法在模块划分中的应用研究
2021-11-22赵跃,单泉,陈砚,孔芝
赵 跃,单 泉,陈 砚,孔 芝
(东北大学秦皇岛分校控制工程学院,河北 秦皇岛 066004)
1 引言
模块化设计是指在对产品进行市场预测、功能分析的基础上,综合考虑产品对象,划分并设计出一系列的功能模块;然后根据用户的要求,对模块进行选择和组合,迅速组合成不同功能、或功能相同但性能不同、规格不同产品的一种设计方法。
当前新一轮科技革命主导的新一轮工业革命正在到来,这也正是中国从制造大国走向制造强国的历史性机遇。模块化设计可以有效支持创新,符合创新驱动的发展战略。通过使用模块化设计,能够有效降低产品开发设计复杂性、缩短产品开发周期、有效支持企业间的协同创新设计、支持客户参与产品开发设计[1]。
模块划分是模块化技术中的基石,模块划分方法根据形式可分为传统模块划分方法和基于智能优化算法的模块划分方法。文献[2-4]基于模糊聚类的方法对相应产品进行了模块划分工作,取得一定的成果。然而模糊聚类方法在阈值的确定上往往需要反复尝试,工作量较大,且对于组件数量较多的模块划分问题,矩阵的变换分割也较为复杂。
因此,随着计算机技术的发展,基于智能优化算法的模块划分方法也得到了长足的发展。遗传算法被文献[5-6]等广泛应用于模块划分工作;文献[7-8]等在此基础上,将遗传算法与模拟退火算法融合,使原算法性能加以提高;文献[9-10]等将免疫算法进行改进用于模块划分;离散粒子群算法也被文献[11]等引入该领域;文献[12]采用猫群算法进行软硬件的划分,也取得了较好的效果。然而现阶段基于智能优化算法的模块划分方法的发展对模拟退火算法、遗传算法、免疫算法、粒子群算法等成熟算法的依赖性较大,且以上算法在迭代精度、速度上存在一定的瓶颈,一些新算法仍有待于引入模块划分工作中。将野草入侵算法加以改进引入模块划分中,为模块划分算法的设计与实现提供了一种全新的思路,对模块化设计将起到一定的推动作用。
2 算法简介
野草入侵算法是一种基于种群的无衍生优化算法,其灵感来自田间杂草的殖民化。该算法具有入侵性、稳健性以及适应环境变化等特性[13]。
野草入侵算法有四个主要步骤:初始化、繁殖、空间分布和竞争排斥。在初始化步骤中,在搜索域随机生成一定量的个体,组成初始种群;繁殖个体,每个个体根据其适应度值产生种子数量。第三步,使用高斯分布在搜索空间上分布生成的种子,由于新生种子数量与个体的适应度有关,因此使用高斯函数完成空间分布能够有效提高空间搜索的效率;由于繁殖过程,其种群大小在每次迭代时都会增加,因此算法的最后一步是竞争排斥,通过从群体中移除最差的个体来限制最大允许群体大小至规定值,从而控制群体大小。
与传统遗传算法相比,野草入侵算法不需要交叉变异等操作,因此其操作简洁,计算效率高,运行时间短。但其新生个体的策略导致了算法由全局搜索逐步转变为局部搜索,使其全局搜索能力不强,易于陷入局部最优。此外,该算法的随机搜索特性对其收敛速度也存在着一定的影响。
3 改进的野草入侵算法在模块划分中的应用
野草入侵算法创立之初,是为了解决多元函数的最小值求解问题。与多元函数极值问题不同,组合问题中解空间的各个维度并不存在最优值,且存在着相互关联,其最优解决定于分组情况。将该算法应用于模块划分中,需要对算法做出适当的修改,以满足其约束条件以及使用要求。
首先,模块的组成需要满足以下两个约束条件:任意模块之间不能含有相同的元素;所有模块的集合构成待划分元素库的整体。针对以上条件,对该算法中各个部分加以修改,修改后应用于模块划分的野草入侵算法流程,如图1所示。

图1 应用于模块划分的改进野草入侵算法流程Fig.1 Flow of Improved Weed Invasion Algorithm Applied to Module Partitioning
以求取适应度函数最大值时的分组方式为例,采用MATLAB进行程序编写具体步骤如下:
(一)初始化种群,随机生成N0个模块划分的形式,针对每个个体,其模块划分结果将是相互独立的。由经验公式,模块划分中默认模块数目的最大整数)。根据确定的模块数量求取方式,确定模块数量,将n个代表元素代码的数字随机存入代表模块的元胞(cell)中,并确保每个元胞中均存在元素。通过该方法完成模块划分,并分别求出每个个体对应的适应度函数值,完成种群初始化的工作。
(二)根据适应度函数值对种群从大到小进行排序,并记录每次迭代的最大值与最小值。
(三)结合所记录的最大值与最小值,计算每种分组方式对应的新种子个数。使用如下的式(1)用于新种子个数的求解。

(四)对原算法进行改进,根据求得的新生种子数量,对选定的个体进行邻域的搜索,以替代在一定范围内随机生成新种子的操作。即选取任意模块中任意组件,将该组件放入任意其他模块中,完成模块的重新生成,并重新求解在该分组情况下的适应度函数值。需要指明一点,为了使重组后的模块划分不存在空模块的情况,被选中迁出组件的模块原组件数必须大于1。
(五)将原始种群与新生个体进行合并,组成新的种群,之后按照适应度函数值从大到小对新种群进行排序。由于新个体的加入,每次迭代种群中个体数量都会有所增加,因此通过从群体中移除最差的个体(即排名末位的个体)来将种群中个体数量减小至Nmax,从而达到竞争排斥的效果。
(六)当满足迭代终止条件时,退出迭代,输出最大的适应度函数值以及与之相对应的最佳模块划分方式。
保留原算法中新生种子个数的计算方式,使新生种子对原有种群优良性状的继承性得到增强,且提升算法对最优解的探索效率。同时,借鉴邻域搜索操作,代替野草入侵算法中的以正态分布随机生成种子的方法,增强算法的全局搜索能力,能够弥补其在全局收敛上表现较差的情况,改善其容易陷入局部最优值的问题,增强该算法的稳健性,确保算法在每次优化过程中均能收敛到其全局最优的模块划分方案上。
同时选用野草入侵算法中的竞争排斥机制进行较差个体剔除的工作,减少算法迭代中的计算量,保持算法简洁易于操作的特性,提高程序的运行速度,保证了算法迭代的高效性,并能够有效解决陷入局部最优值的问题。与此同时,另一个重要改进在于在算法中进一步删除种群变异、随机生成新生种子等操作,进一步简化算法,从而能够保证算法收敛的速度与准确性。
4 实例验证
为了验证本方法的正确性且不失一般性,分别以文献[15]中24个元件的直齿轮减速器以及文献[16]中24个元件的锥齿轮三级减速器作为实例1与实例2进行验证。适应度函数值由式(2)给出。实例1的最优适应度函数值是0.32749,其最优模块划分结果是{1,2,9,10,19}、{3,4,11,12,13,20,23}、{5,6,14,15,16,21,24}和{7,8,17,18,22};实例2最优适应度函数值是0.4399,其最优模块划分结果是{1,5,17,18,19}、{2,6,9,11,14,20,23}、{3,7,10,12,15,21,24}和{4,8,13,16,22}。
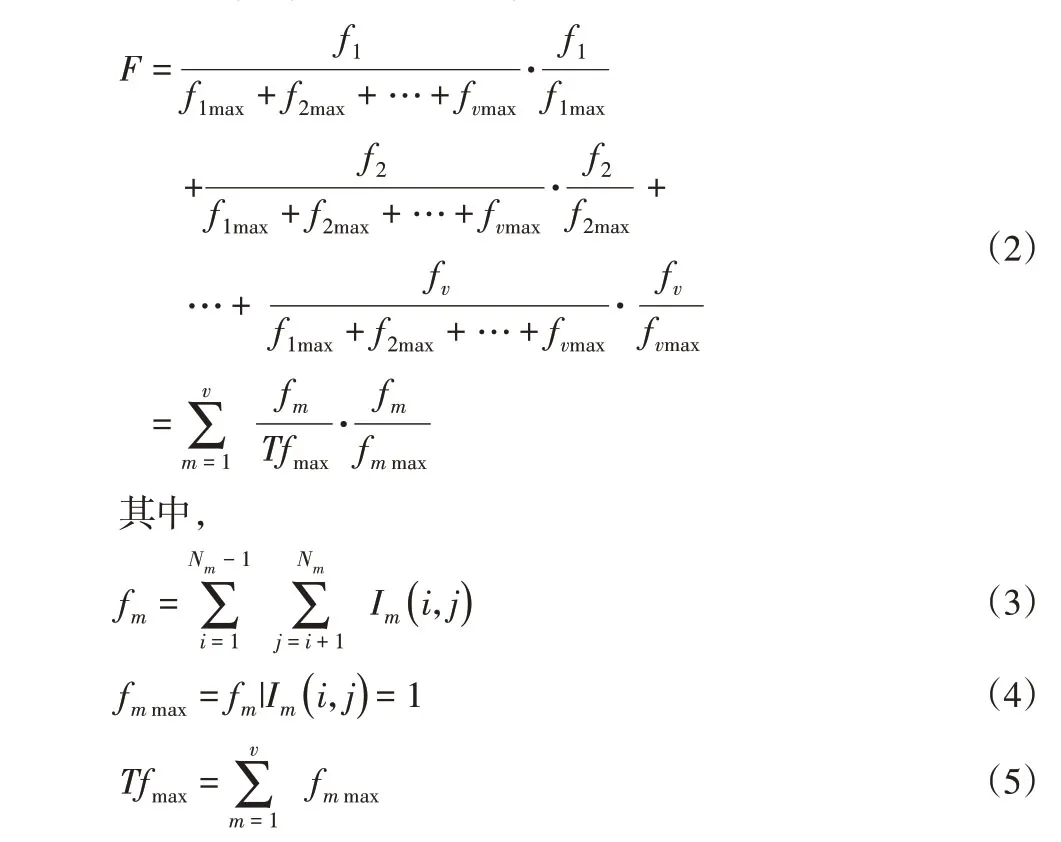
其中,Im(i,j)—第i个组件与第j个组件之间的相关度,即设计结构矩阵中第i行第j列元素的取值。
设定模块数量为4,设定其初始种群数量为50,最大迭代次数500,最大种子最大值为4,最小值为0,实例1使用改进的野草入侵算法进行模块划分,当迭代到第37 次时,适应度函数值收敛,得到适应度函数的最优值0.32749,模块划分结果与文献[15]相同;实例2使用改进的野草入侵算法进行模块划分,当迭代到第31次时,适应度函数值收敛,得到适应度函数的最优值0.4399,模块划分结果与文献[16]相同。证明应用于模块划分的改进的野草入侵算法是一种有效的模块划分算法。
为了进行对比,加入标准野草入侵算法、粒子群算法、遗传算法、免疫算法进行相同的分组。设置各个算法初始种群数量均为50,最大迭代次数500。野草入侵算法的最大种子最大值为4,最小值为0;粒子群算法的位置最大最小值为4和1(位置最大值代表模块个数),速度最大值为2;遗传算法的变异概率为0.2,交叉概率为0.6,选择精英个数为10;免疫算法的克隆亲本个数为10,克隆数量为5,突变概率为0.5。分别得到最优模块划分结果,优化曲线,如图2所示。其中上半部分为实例1的优化曲线,下半部分为实例2的优化曲线。

图2 五种算法的优化结果对比图Fig.2 Comparison of Optimization Results of Five Algorithms
由图可知,在两个实例中,改进的野草入侵算法均达到最快的收敛。为了不失一般性,将以上各个算法重复运行50次,对运行时间、最快收敛代数、最慢收敛代数、平均收敛代数,收敛代数的标准差几个参数进行考察,如表1所示。

表1 五种算法结果对比Tab.1 Comparison of the Results of the Five Algorithms
由以上两个实例可知,改进的野草入侵算法与其他算法相比,性能提升较为明显,且在运行速度和收敛速度上均大幅优于其他四种算法,且收敛代数的标准差最小,说明了该算法较强的鲁棒性。由此可知应用于模块划分领域的改进的野草入侵算法是一种高效且准确可靠的算法。
5 模块划分软件系统的编写
基于以上结果,参考设计人员的工作习惯,并提高模块划分的效率,增加算法整体的可移植性,采用Python3.7开发人机交互的最优模块划分结果求取的软件系统,其主界面,如图3所示。

图3 模块划分系统主界面图Fig.3 Main Interface Diagram of the Module Partitioning System
其后台迭代程序仍采用如图1的算法流程进行编写,在此基础上对迭代过程中的适应度函数加以改进,采用如下公式进行迭代计算。

与式(2)类似,其中,N—组件数量之和;Nm—第m个模块的组件数量;r—模块数;Im(i,j)—整体结构设计矩阵中第i行j列元素;Ck—模块内得组合数。
式(6)中第一项可作为各个模块中组件数量相似性的度量,即可对模块划分结果中各个模块中组件数量的平均程度加以保障;第二项中的分子与分母分别为内聚度和耦合度的表征。因此当模块划分结果呈现出“高内聚、低耦合”特性,且各模块中组件数量近似相等时,适应度函数取得最大值。
应用本软件系统,用户可以完成的主要功能有:用户输入结构设计矩阵的保存、已存在结构设计矩阵的读取、最优组合结果的输出、迭代过程的显示与储存。仍采用文献[15]中的实例对该软件系统的使用过程进行说明,使用过程如下:
首先,用户在组件数量对话框中输入组件数量24,点击右侧“创建结构设计矩阵”按钮,在界面中按照顺序输入各个组件之间的相关度,完成结构设计矩阵的建立,点击“保存”,将结构设计矩阵保存为Excel表格文件,如图4所示。

图4 创建结构设计矩阵顶级窗口Fig.4 The Top-level Window for Creating the Design Structure Matrix
之后,点击“请选择结构设计矩阵”后的“点击选择”按钮完成文件的读取的工作,此时文件所对应的路径便会显示在右侧的文本框中。之后,通过复选按钮确定参与计算的结构设计矩阵,并对其设定相应的权重值。最后,通过右侧三个单选按钮对结果的显示与保存方式进行选择,即可完成最佳分组情况计算前的准备工作。准备工作结束后,点击开始迭代按钮,迭代过程与分组结果即显示在文本框中,如图5所示。此时根据输出结果显示,计算后的最佳分组是{1,2,9,10,19}、{3,4,11,12,13,20,23}、{5,6,14,15,16,21,24}和{7,8,17,18,22},与文献[15]中结果相同,证明本软件系统在模块划分中的真实可靠性。

图5 迭代过程与模块划分结果的显示Fig.5 Iterative Process and Display of Module Partitioning Results
本软件基于模块划分的步骤,使设计人员通过创建、选取加载结构设计矩阵并设置相应的权重等过程,求得最佳分组结果及其所对应的适应度函数值,并可以根据用户的需求显示并保存所需结果。软件整体使用流程符合设计人员的设计习惯,能够有效提高设计人员的设计效率,减少重复性劳动,对模块化设计起到较大的促进作用。
6 结束语
将野草入侵算法加以改进应用于模块划分中,改变原算法中新生个体的操作,并删除种群变异、随机生成新生种子等操作,使程序编码简洁,算法易于实现,且新算法兼顾收敛速度与准确性两个重点,与原算法相比在性能上有较大的提升。并通过实例验证,证明了该算法的可行性,为模块划分算法的设计提供了一种新的思路。并且将该算法与粒子群算法、遗传算法、免疫算法进行比对,证明了该算法在模块划分中的高效性。并基于该算法,开发出模块划分软件系统,以提高设计人员的设计效率,减少重复性劳动,促进模块化设计的发展。
