基于等强度理论压气机轮盘结构优化分析

尚永锋，冯天杰，付为刚

（中国民用航空飞行学院航空工程学院，四川 广汉 618307）

1 引言

轮盘是压气机完成功能转换的重要零件，在工作时承受着极大的负荷。轮盘转速通常都达到每分钟数千转到数万转。轮盘除了固定叶片和承受自身的离心力外，还要承受叶片巨大的离心载荷。因为叶片和轮盘产生的离心载荷很大，所以轮盘需要设计较大的盘心承载，导致轮盘质量增加，同时轮盘的体积也会随之增大[1]。不仅使发动机气动外形设计难度增加，更甚者轮盘发生破坏，产生的高能碎块损坏机匣，影响飞行安全[2-5]。因此随着优化技术的发展，通过数值与仿真分析对发动机盘体寻求一种简洁、高效的优化方式来满足轮盘轻质化设计的需求也更具有研究意义和价值[6]。

对于轮盘结构优化设计的研究，大部分文献都是以有限元分析为基础，或开发独立的优化计算模块，或借助现有的软件优化平台。常见优化设计所涉及的优化算法包括了传统的SUMT法、拉格朗日乘子法等，以及Kriging方法、遗传算法等现代智能算法。文献[7-8]使用ANSYS软件对发动机高负荷涡轮盘进行了结构优化设计，将单幅板结构改为双幅板结构来实现轮盘的减重。文献[9]选取轮盘的结构尺寸作为优化变量，建立了轮盘结构优化模型，通过整体结构优化提高轮盘设计的材料利用率，可将轮盘质量减轻10%。文献[10]采用Isight优化平台，将轮盘质量设定为目标函数，以最大周向应力和低循环疲劳寿命为约束，对轮盘结构进行优化，并通过对轮盘参数的研究，分析了各参数与目标变量之间的关系。

对于轮盘结构优化设计的研究，大部分文献都是以有限元分析为基础，或开发独立的优化计算模块，或借助现有的软件优化平台。常见优化设计所涉及的优化算法包括了传统的SUMT法、拉格朗日乘子法等，以及Kriging方法、遗传算法等现代智能算法。文献[7-8]使用ANSYS软件对发动机高负荷涡轮盘进行了结构优化设计，将单幅板结构改为双幅板结构来实现轮盘的减重。文章[9]选取轮盘的结构尺寸作为优化变量，建立了轮盘结构优化模型，通过整体结构优化提高轮盘设计的材料利用率，可将轮盘质量减轻10%。文献[10]采用Isight优化平台，将轮盘质量设定为目标函数，以最大周向应力和低循环疲劳寿命为约束，对轮盘结构进行优化，并通过对轮盘参数的研究，分析了各参数与目标变量之间的关系。

利用ANSYS优化平台，以轮盘的体积作为优化目标，以某型高负荷压气机轮盘为例，考虑轮盘所承受的载荷过大，按照轮盘设计准则所规定的关键应力约束作为优化限制，确保轮盘与叶片连接处的尺寸在优化中保证足够的应力强度，并依照等强度理论对轮盘的几何尺寸进行约束，提出并建立轮盘结构优化设计数学模型及方法，对轮盘优化前和优化后进行对比分析，以说明压气机轮盘结构优化设计的关键和使用ANSYS一阶优化方法对轮盘优化的优势。

2 轮盘简化设计方法

2.1 基于等强度理论轮盘优化设计

为了在简化设计中确保轮盘整体结构强度满足规定的强度要求，可以采用等强度理论对轮盘进行设计。等强度理论是指让轮盘各位置的径向和周向应力都等于某一常数，这样设计出的轮盘质量最轻[11]。航空发动机压气机盘近似工作在等温的情况下，满足等强度盘只有等温盘的情况下才能实现等强度设计的要求。

2.2 轴对称假设

虽然轮盘结构十分复杂，但其几何形状通常都是对称的。因此在实际设计中对轮盘提出了轴对称假设，既包括几何形状，载荷分布以及温度场和约束条件情况等都对称于某轴[12]。

同样轮盘中所有的应力分量、应变分量和位移分量也都对称于这一轴。这种问题称为空间轴对称问题。利用轴对称假设便可以极大的简化轮盘设计。由于盘外缘的应力很复杂，我们只研究盘本身的应力，轮盘简化结构，如图1所示。这样轮盘就可以看作是由一个截面如图2所示绕指定轴旋转而成。那么问题就可以简化成对一个截面的分析[13]。

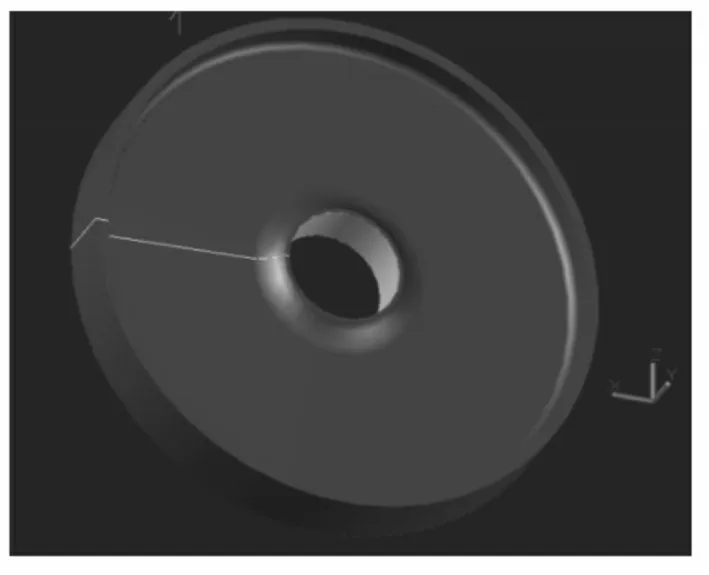
图1 压气机轮盘模型Fig.1 Compressor Disk Model

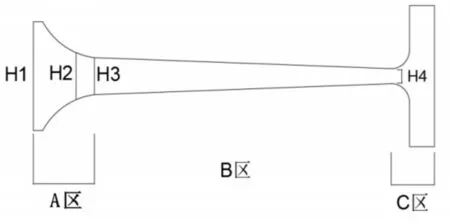
图2 轮盘区域分布Fig.2 Disc Area Distribution

3 基于ANSYS轮盘结构优化设计

3.1 轮盘结构优化

以EJ200 发动机压气机轮盘工作温度为213℃为例。其主要结构参数为：盘外缘半径为228mm；盘内径为50mm；轮缘宽度为60mm；轮缘厚度初始设为H=11mm轮盘转速n=15000r/min；盘外缘分布面载σa=12.83MPa；盘材料用TC11钛合；密度ρ=4480kg/m3；可查出轮盘在T=213℃下的材料参数：轮盘弹性模量E=105GPa；泊松比ν=0.3；许用应力σ=570MPa。为了防止轮盘有害变形和破裂。轮盘需满足子午面平均周向应力和圆柱面最大平均径向应力的约束。

轮盘可分为三个区域，如图2所示。即A区、B区和C区，其中A区是为了消除等强度盘盘心处的应力集中所设计的盘体；B区即为等强度盘体，是根据等强度理论设计的；C区是用来连接叶片的，由于工作中轮盘和叶片都高速运动，连接处需要承受巨大载荷在优化调整中一般不进行改动。所以优化轮盘时只对A区和B区的尺寸进行优化[14]。轮盘的初始参数，如表1所示。轮缘处的倒角半径初步设定为R=8mm。根据轮盘初始结构在ANSYS中通过定义变量、建立模型，分化网格，定义边界条件，计算求解等步骤。对初始轮盘进行强度分析得到其等效应力分布，如图3所示。

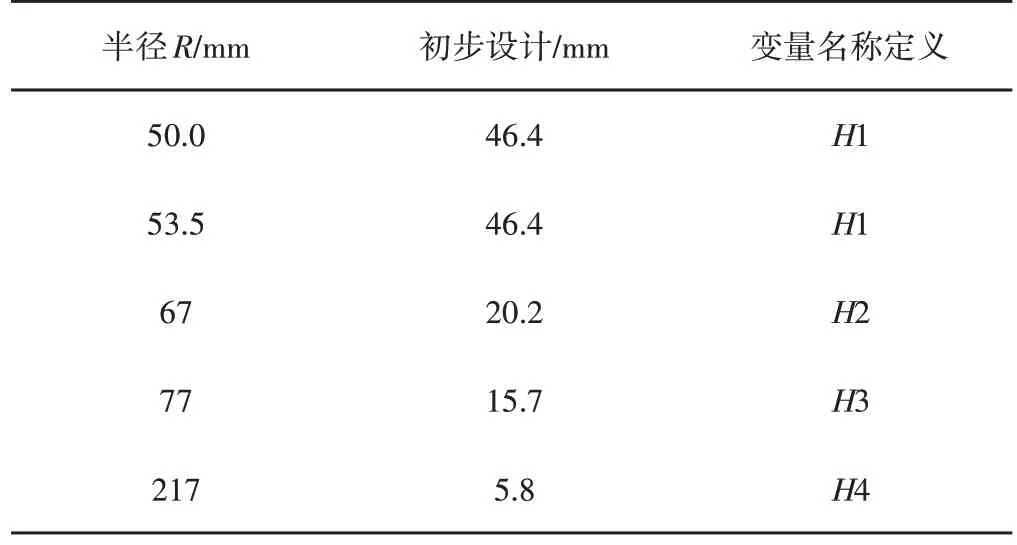
表1 轮盘初始设计参数Tab.1 Initial Design Parameters of Disc

图3 初始轮盘等效应力云图Fig.3 Cloud Chart of Equivalent Stress of Initial Disc

3.2 优化过程

首先根据轮盘初始结构在ANSYS中通过定义变量、建立模型，分化网格，定义边界条件。通过限制所有节点等效应力STR不超过570MPa，将体积V设定为目标函数，使用一阶优化方法进行优化。一阶优化方法通过因变量的一阶偏导数确定在设计空间内的搜索方向[15]。

在ANSYS 中读取所分析的数据，轮盘初始体积为V=0.0025344m3。从主菜单中选择Main menu：General Postproc＞List Results＞Sorted Listing＞Sort Nodes，在打开的对话框中选中图4-3所示的设置，读取等效应力，并在命令输入框中输入“*GET，STR，SORT，MAX”，读取最大等效应力。最后所读取的参数都在参数栏里，如图4所示。

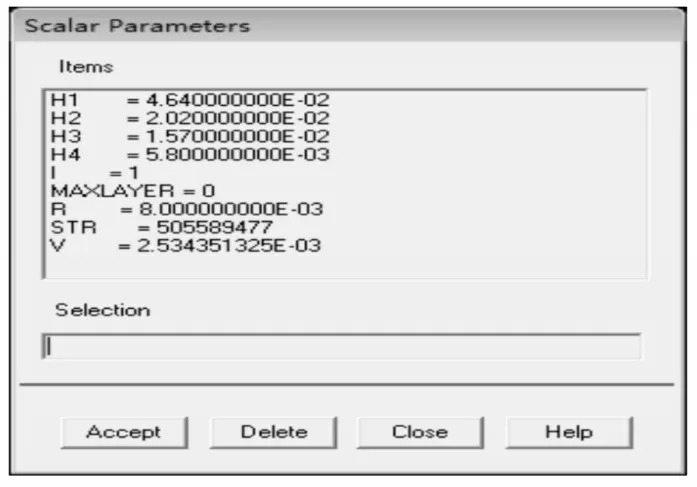
图4 优化参数Fig.4 Optimization Parameters

然后将此时的数据保存，打开Design Opts写入刚才保存的DB文件。读入后开始对设计变量进行设置。并对H1，H2，H3，H4，和R设定变化区间。其次再对状态变量进行定义，将STR定义在（10～570000000）之间，容差为10。然后对目标函数V 进行设置，其收敛判据为0.00001。最后从主菜单Design opt＞Method/tool，选择First-order，设置最大迭代次数为20。然后在主菜单中Main menu：Design opt＞Run 进行优化求解。经过九次迭代达到最优解。从主菜单中选择Main menu：Design opt＞Design Sets＞Graphs/Tables.在X 轴列表框选择Set numbers，在Y 轴列表框中选择V，单击Ok，图像显示优化变量的变化过程，如图5所示。

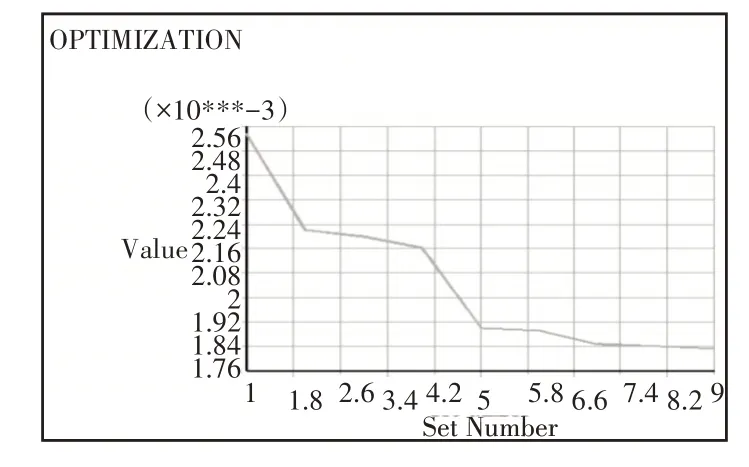
图5 优化变量的变化过程Fig.5 Change Process of Optimization Variables

由图5可以看出在迭代计算的第9次运算，就中断了优化，就表示在第九次的时候已经达到最优解了，此时的von mises stress图，如图6所示。这样我们从轮盘优化结果中读出一组数据，如图7 所示。图中第九组数据可以读出在满足最大应力562MPa＜570MPa，满足材料限制，其优化后的体积V2为0.0018250m3。

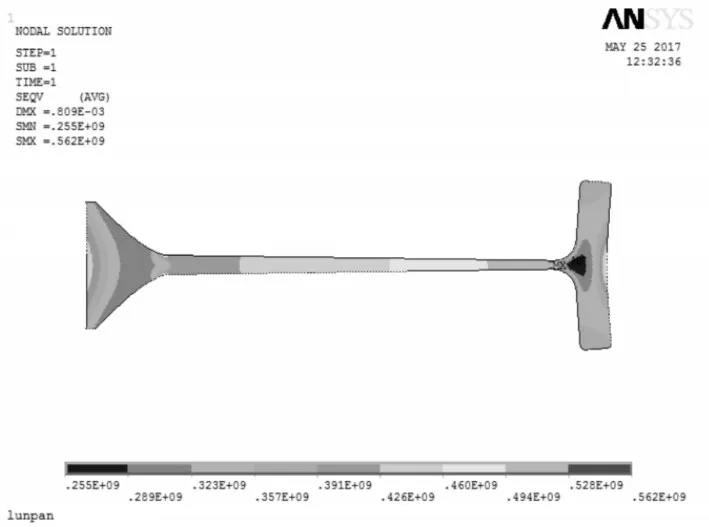
图6 优化后等效应力图Fig.6 Optimized Equivalent Stress Diagram

图7 轮盘优化结果Fig.7 Optimization Results of Disc

3.3 优化结果分析

优化后的周向应力云图，如图8所示。

图8 优化后的周向应力云图Fig.8 Cloud Chart of Optimized Circumferential Stress

由图6与图8可以看出，优化后的轮盘有效的改善应力集中问题，并用公式（1）将优化前与优化后轮盘体积进行计算，得到轮盘体积减少了27.99%。

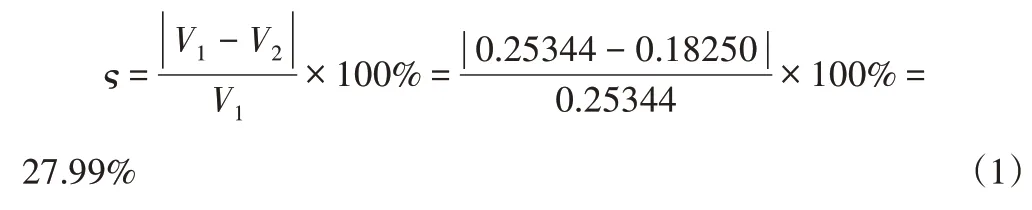
式中：V1，V2—优化前后轮盘体积，单位m3。

4 结论

（1）运用ANSYS对轮盘进行了优化设计的结果显示，基于等强度理论优化设计轮盘，应力集中现象减少，应力分布优于传统设计。（2）确保轮盘应力强度的同时，通过结构优化使得轮盘整体体积减少了27.99%，提高轮盘材料利用率的同时，减轻发动机重量，对提高发动机推质比有极大的参考意义。（3）一阶优化轮盘应力强度由低到高，慢慢贴近约束强度，轮盘体积慢慢减小，显示了一阶优化的稳定与可靠性。