基于NURBS曲面建模的山区公路边坡变形监测研究

刘洋洋， 张大磊， 宋辛辛， 王德生

（郑州师范学院地理与旅游学院，郑州 450044）

对边坡不同时期的变形值进行监测分析，可以全面了解边坡的整体变形情况，并从中找出潜在的地质灾害隐患点（变形值较大的危险区域），从而可为后续的边坡灾害防治工作提供有力的决策支持和信息支撑［1-3］.近年来，伴随科技的快速发展，很多的新方法、新理论以及新技术被引入到了边坡变形分析研究中，其中比较具有代表性的就是三维激光扫描技术［4-6］，该技术突破了传统的单点测量方式，能够快速准确地采集目标地物的三维点云数据［7］，如今已被广泛应用于边坡变形分析研究中. 国外方面，Ghuffar等［8］通过机载激光扫描仪（ALS）和地面三维激光扫描仪（TLS）对奥地利某活跃滑坡采取了长达9年的变形监测；Fey等［9］基于机载激光扫描系统对阿尔卑斯山脉某段边坡进行了长期形变监测；Spreafico 等［10］基于三维激光扫描技术和离散元模型，构建了一种新型边坡稳定性评价方法，并对意大利圣莱奥某公路边坡进行了变形分析. 国内方面，赵小平等［11］系统阐述了基于三维激光扫描技术的变形分析原理，并以某边坡为例，进行了变形分析监测；黄江等［12］基于三维激光扫描技术对某边坡危岩体进行了定量分析，并在点云数据处理软件的支撑下构建了边坡危岩体稳定性评价系统；李滨等［13］系统介绍了三维激光扫描技术在边坡监测中的技术优势、实现原理以及实现流程，并以某边坡为例，进行了应用分析.

在国内外学者专家的共同努力下，基于三维激光扫描技术的边坡变形监测研究取得了很大进展，但目前仍然存在很多急需解决的难点问题，比如基于激光点云数据的山区公路边坡高精度模型构建问题. 在构建山区公路边坡模型时，由于山区地形崎岖复杂且高低不平，采用传统的DEM建模技术和三角面片建模技术，其模型效果都不是很理想，比如说构建的边坡三角面片模型表面往往会出现很多裂隙和孔洞，而且其对边坡地形的表达也比较粗糙且不够准确完整；其次，构建的边坡DEM模型虽然对边坡细节的表示相对完整准确，但一般只适用于表面较为平坦光滑的边坡，在面对坡面高低不平、地形地势复杂多变的山区公路边坡时，边坡DEM模型对坡面细节就很难进行完整准确的表达，也就难以有效反映边坡表面地形的真实起伏状态. 由上述内容可知，目前需要对山区公路边坡特点进行系统研究，并在此基础上，引进一些合适有效的新方法来实现山区公路边坡高精度建模工作，针对上述问题，本文将NURBS曲面模型重建技术引入到山区公路边坡精细模型构建中，并选取太行山区X012公路双影线附近几处典型山区公路边坡为例，进行变形监测应用分析.

1 NURBS曲面建模基本原理及实现流程

1.1 NURBS曲面建模基本原理

NURBS（Non-Uniform Rational B-Spline），即非均匀有理B 样条，是Versprille 博士提出的一种新型曲面模型重建方法［14］. 其中，Non-Uniform指不均匀性，也就是表示在构建不规则曲面模型时可以任意改变某个控制顶点的影响力范围，这非常利于不规则曲面的构建；Rational表示有理，其主要含义是指能够通过有理多项式来对所有的NURBS 曲面模型进行合理表达；B-Spline 表示B样条，它主要是指能够通过路线来构建一条曲线，并且能够以内插值的形式在一个或多个点之间进行替换［15］.

NUBRS曲面建模技术是专为曲面复杂物体三维模型重建而设计的，它能基于曲线和曲面的形式对目标地物三维模型的轮廓和外形进行准确精细的表达. NURBS曲面模型重建技术拥有非常高效的数学表达方式，它能够利用同一种数学模型对初级曲线曲面、二次曲线曲面以及自由曲线曲面等进行准确表示，其表达公式：

式中：Pi表示控制顶点；t表示控制参数；ci表示控制顶点Pi的权因子，曲面偏离点的程度由ci数值的大小来决定；Ni,k(t)主要指k次B样条的基函数；Ri,k(t)表示节点矢量上的k次有理基函数.

相比其他建模方法，NURBS曲面模型重建方法更适用于对复杂地物进行三维建模，它能够准确还原复杂地物的表面细节及地形地貌特征. 假设有一张p×q次的NURBS曲面，其数学表达方式为：

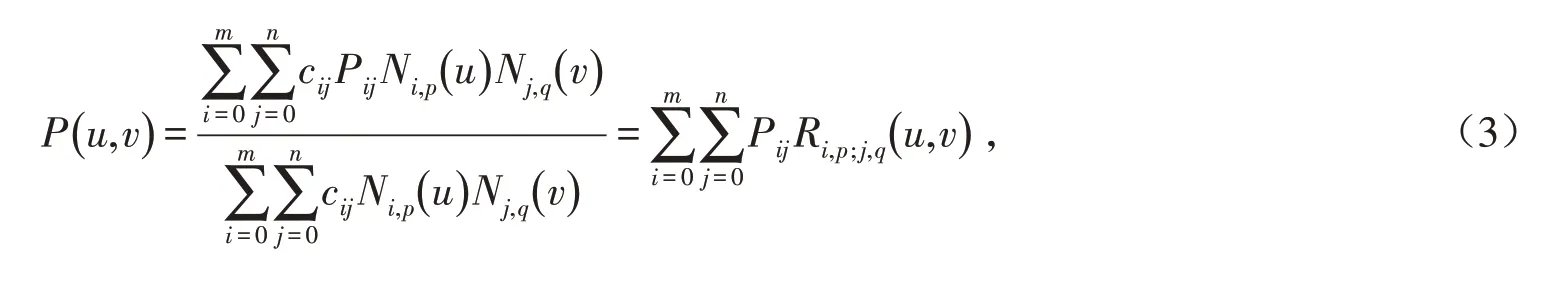
式中：Pij表示控制顶点；cij为控制顶点Pij的权因子，其数值能够决定曲面偏离点的程度；Ni,p(u)为u向p次的规范基；Nj,q(v)为v向q次的规范基.

1.2 NURBS曲面建模实现流程

与平原地区的平坦公路不同，山区公路地质环境复杂多变，地势高低不平，在雨雪、地震、日晒、强风、植被生长、地下水活动等内外力作用下，导致边坡土壤疏松、岩土突出且坡面粗糙，而且其表面会产生很多碎岩块［16］. 通过观察边坡点云数据可知，山区公路边坡点云起伏变化较大且分布的很不均匀，如果基于边坡点云构建DEM模型可能无法有效还原边坡真实起伏状态，而选用专门针对复杂地物（山区公路边坡）进行精细建模的NURBS 曲面模型重建方法是一种优良选择. 曲面建模方法不仅能够对边坡表面的曲线度进行精准调控，而且还能修补还原海量的边坡细节，从而使曲面模型更加贴合边坡实际起伏形态. NURBS曲面建模流程如图1所示.

2 NURBS曲面建模效果对比试验

为了对NURBS 曲面模型重建效果进行验证，以太行山区某公路边坡局部区域为例，分别利用DEM建模方法、三角面片建模方法以及NURBS 曲面建模方法，对该区域进行模型重建，并对这3 种模型效果进行对比分析，边坡局部区域位置及原始点云数据效果如图2.

图2 边坡局部区域位置及其原始点云Fig.2 Local location of slope and original point cloud

如图3所示，通过对3种方法的边坡建模效果进行对比研究，可以得出以下结论：

图3 研究区3种模型效果对比Fig.3 Effect comparison of three models in the study area

1）将3种边坡模型重建效果和边坡实际情况进行对比，可以发现，边坡三角面片模型表面存在着大量裂缝和孔洞，而且三角面片模型对边坡表面细节的表达也比较粗糙且不够完整. 与之明显不同的是，边坡NURBS曲面模型和边坡DEM模型对边坡表面细节的表达都相对良好且完整，没有发现较为明显的裂缝和孔洞.

2）对边坡NURBS曲面模型和边坡DEM模型进行对比分析可以看到，相比边坡DEM模型，边坡NURBS曲面模型表面平滑且细腻，其对边坡地形细节的表达更加丰富和完整.

3）以地形拟合度为量化对比标准，选取边坡NURBS曲面模型和边坡DEM模型同一区域的网格节点作为样本点，基于Matlab仿真模拟软件对该区域的NURBS曲面模型和DEM模型地形拟合度进行比对分析，具体结果如图4.

图4 两种模型的边坡地形拟合效果对比Fig.4 Comparison of slope terrain fitting effect between the two models

从图4中可以看出，两种方法构建的边坡模型都能对边坡整体地形进行有效拟合，但在边坡局部细节方面，比如在图3中边坡左侧不规则突变区域，边坡NURBS曲面模型对边坡地形的拟合度要更优于边坡DEM模型. 由于山区公路边坡表面地形复杂多变，其表面存在很多的不规则突变区域，因此，在对构建山区公路边坡表面模型时，相比边坡DEM模型和边坡三角面片模型，边坡NURBS曲面模型对边坡表面地形表达更为完整丰富，更能贴合边坡表面的真实起伏状态，所以，选用NURBS曲面建模方法对山区公路边坡进行精细建模是一种优良选择.

3 山区公路边坡变形监测应用研究

3.1 研究区概况

经过综合考虑对比，从太行山区附近X012公路双影线公路中选取3处边坡作为研究样本，依次将其命名为1号、2号和3号. 1号属于岩质边坡，2号和3号属于土质岩质二元混合边坡. 研究区大体情况如下：

1）3处边坡均位于太行山区，所处位置地质环境复杂多变、地势高低不平，属于典型的山区地貌. 由实地考察情况发现，研究区部分土质边坡坡体较为松动，坡面雨水冲刷痕迹较明显；部分岩质边坡存在着一些表面风化严重的危岩体，这些危岩体向外突出且呈碎裂状态；另外，还有部分边坡的防护堤年久失修，有破损毁坏的痕迹.

2）研究区周边有多处知名旅游风景区，如青龙峡、净影寺和云台山等. 这些景区附近平时人员车辆较多，尤其是在节假日或双休日，人流量和车流量会达到一个峰值. 此时一旦发生边坡地质灾害，轻则堵断交通，影响公路和旅游景区的正常运营，造成经济损失；重则损毁车辆，砸伤游客. 由上述情况可知，研究区附近边坡具有较高的灾害风险，而且一旦发生灾害，损失较大. 因此，对该区域边坡进行变形监测很有必要，可达到防患于未然的目的.

3.2 构建边坡NURBS高精度曲面模型

试验共采集了3期边坡点云数据，数据获取时间依次为2016年12月1日（冬季）、2017年3月25日（春季）以及2017年9月21日（秋季）. 为了尽量避免植被因素对边坡建模的影响，没有选择在植被覆盖率相对较高的夏季进行数据采集. 基于点云处理软件对边坡原始点云数据进行去噪、滤波和简化等处理后，得到精细坡面点云数据，最后基于NURBS模型重建技术构建各边坡精细曲面模型. 以3号边坡为例，模型效果如图5.

图5 边坡NURBS曲面模型构建Fig.5 Construction of NURBS surface model of slope

3.3 边坡形变位移分析

通过对3处边坡的多期NURBS 高精度曲面模型进行对比分析，找出各边坡的地质灾害隐患点（危险区域）. 在具体分析时，将边坡的形变分析过程按照时间顺序依次分为两大阶段：第一阶段为第一期（2016年12月1日）边坡曲面模型和第二期（2017年3月25日）边坡曲面模型对比分析；第二阶段为第二期（2017年3月25日）边坡曲面模型和第三期（2017年9月21日）边坡曲面模型对比分析. 通过对比分析，可依次得到两大阶段的边坡表面色谱差异图. 通过观察该图可以发现，边坡在不同时期的变形情况，其中冷色调代表负向位移变化情况，暖色调代表正向位移变化情况. 最后，基于分析结果，再结合现场考察情况、《工程高边坡变形量预警标准》相关规定［17］以及专家意见，找出3处边坡中变形量超过规定安全阈值的危险区域（地质灾害隐患点）. 具体情况如图6.

由图6 a 可知，在第一阶段期间（2016 年12 月1 日—2017 年3 月25 日）内，各边坡都存在着一些变形情况. 其中，1号边坡大部分区域都为浅绿色，整体变形值为-0.66～0.66 mm；由图6c可知，2号边坡大部分区域也被浅绿色覆盖，整体变形值为-0.483～0.483 mm；由图6e可知，相比1号和2号边坡，3号边坡大部分区域都是深青色状态，表面在第一阶段时期内边坡表面主要发生了一些负向位移情况，变形值最大约-2.14 mm. 另外，3号边坡也有部分被橙色覆盖的区域，这些区域存在着一些正向位移情况，变形值最大约-2.14 mm. 在该时期内，各边坡变形值都相对较小，整体都处于稳定状态，灾害风险相对较小.

如图6b所示，与第一阶段相比，在第二阶段（2017年3月25日—2017年9月21日），各边坡的变形情况更加严重了一些，其中，红色椭圆形标定的1号边坡深蓝色区域，出现了严重的负向位移情况，负向变形值最高达到了-12.74 mm，除此之外，该边坡右下方出现了一小块深红色覆盖区域，表明该区域存在着较大的正向位移情况，正向变形值最高达到了12.74 mm；如图6d所示，红色三角形标定的4号边坡中部深蓝色区域，产生了较为明显的负向位移情况，变形值最高达到了-9.77 mm；如图6 f所示，红色椭圆标定的5号边坡中部和顶部两个区域，依旧被深蓝色所覆盖，覆盖面积也有所扩大，在第二阶段期间最大变形值达到了-4.06 mm，表明从第一阶段到第二个阶段的两个时期内，这些区域长期存在着负向位移变化，将该区域两个阶段的变形值进行叠加计算，可知两个阶段内该边坡累计变形达-8.14 mm. 由《工程高边坡变形量预警标准》中的相关规定［17］可知，三处边坡某些区域（三角形及椭圆形所标定的部分）的变形值已经超过了安全阈值，具有很高的灾害风险性，可以将其认定为危险区域（地质灾害隐患点），建议当地应急管理部门和公路部门提前对危险区域进行灾害防治处理.

图6 各边坡两个阶段变形分析结果Fig.6 Deformation analysis results of each slope at two stages

3.4 边坡监测结果精度验证

为了验证文中方法变形监测结果的准确性，在采用三维激光扫描技术进行边坡变形监测的同时，基于传统的GPS技术对研究区边坡进行了变形分析，并借助u-检验法对二者的变形监测结果进行精度对比量化分析.

首先，从各边坡中选取3个GPS观测点为样本点，其中P1、P2和P3为1号边坡的观测点，P4、P5和P6为2号边坡的观测点，P7、P8和P9为3号边坡的观测点. 其次，将各边坡观测点的基于三维激光扫描的变形监测结果和基于GPS的变形监测结果进行对比，由于多期模型对比结果主要显示是边坡垂直方向上的变形位移值，因此在具体对比时，也只取垂直方向上的边坡GPS变形监测结果进行对比分析，对比结果如表1所示.

表1 两种方法变形监测结果对比情况Tab.1 Comparison of deformation monitoring results of the two methods 单位：mm

由表1可知，基于三维激光扫描技术的边坡变形监测结果和边坡GPS变形监测结果基本一致，两种方法在各个观测点上的变形监测结果差值在±1 mm之内. 为了能获取更加客观准确的精度量化分析结果，基于u-检验法对二者的变形监测结果差值进行定量分析. 在具体计算时，基于二者的差值，首先求出差值平均值u，则有：

其次，求出差值的标准值σ，则有：σ=±0.307 3 mm.

然后，在平均值u和标准值σ的基础上，对二者进行u-检验分析，则有：

式中：μ0为检验结果；n为观测点个数，n=9 .

最后，将计算求出的检验结果和检验水准进行对比分析，参考检验规则，将检验水准c取值为0.05，查询正态分布表［18］可知：uc/2=1.96 . 由于u0=0.955<1.96=uc/2，所以，基于u-检验法的验证标准可以得出以下结论：基于三维激光扫描的边坡变形监测结果和基于GPS的边坡变形监测结果具有良好的一致性，由此可证明三维激光扫描技术支持下的边坡变形监测结果具有较高的精确度. 同时，这也说明了基于三维激光扫描和NURBS曲面建模技术对山区公路边坡进行变形监测是可行且有效的.

3.5 边坡变形规律分析及灾害防治建议

基于各边坡不同阶段的变形分析结果，再结合实地考察情况和专家意见，对3处边坡的变形规律进行总结归纳，并提出相应的防灾减灾建议.

1）由图6中各边坡变形分析结果可知，相比第一阶段的变形情况，3处边坡第二阶段的变形情况要更加严重一些. 究其原因，是因为第一阶段的两次边坡点云数据采集时间分别为冬季和春季，这两个季节都是少雨季节，由研究区降雨量统计数据可知，在第一阶段期间，研究区降雨量相对较少，降雨强度也较小，各边坡受雨水冲刷的影响相对较小，边坡变形情况不太明显，变形数值也相对较小；与之不同的是，第二阶段边坡两次点云数据采集时间分别为春季和夏季，期间为多雨季节，由研究区降雨量统计数据可知，在第二阶段时期，研究区降雨量相对较多，降雨强度也较大，还多次发生了暴雨和强降雨，各边坡受雨水冲刷的影响相对较大，因此与第一阶段相比，各边的变形情况更为严重. 综上所述，研究区各边坡受降雨影响较大，其变形值的大小和降雨量有关，因此在降雨天气下，建议车辆和行人经过研究区各边坡时，注意安全，不要逗留.

2）通过对各边坡两个阶段的变形进行对比可以看出，相比3号岩质边坡，1号和2号这两个土质岩质二元混合边坡的变形面积要更大些. 这是由于二元混合边坡表面有大量的土块和碎岩块，在雨水的冲刷作用下，很容易出现大面积沉积或下滑，而岩质边坡表面基本由坚硬岩块构成，受降雨影响的作用相对较小，雨水很难将大面积岩石冲刷变形. 正常情况下，只有一些相对突出或者松动的危岩体区域才会出现变形情况，这一般是由于危岩体上的破碎岩块持续向下掉落造成的.

3）在防灾减灾方面提出两点建议：第一，对于各边坡中被三角形或椭圆所标定的变形较大的区域，也就是危险区域（地质灾害隐患点），建议应急管理部门或公路部门派遣专业技术人员对以上区域进行认真排查，并制定具有针对性的防灾减灾措施，在灾害发生之前，提前把安全隐患消除，从而达到防患于未然的目的；第二，建议基于各边坡的实际情况，因地制宜，在各边坡的危险区域（地质灾害隐患点）周边设立安全警示牌.

4 结论

1）在采用三维激光扫描技术进行边坡变形监测时，为了获取更高精度的山区公路边坡模型和更准确的变形监测结果，将NURBS曲面建模方法引入到了该领域中. 研究结果表明，与边坡DEM模型和边坡三角面片模型相比，边坡NURBS曲面模型具有更高的精度，对山区公路边坡地形的表达更加完整和精细，对复杂地形边坡的拟合度也更好，模型效果更加贴合山区公路边坡地形的真实起伏状态. 由此说明，将该方法应用到山区公路边坡高精度建模中是有效且可行的，从而也为该领域的研究提供了一种新参考.

2）以太行山区X012公路双影线几处边坡为例，基于三维激光扫描技术和NURBS高精度曲面模型重建技术，进行变形监测应用研究. 研究结果表明，本研究方法的变形监测结果和边坡GPS变形监测结果基本一致，体现出了良好的准确性；通过变形监测，准确找到了研究区各边坡变形情况较为严重的危险区域（地质灾害隐患点），并提出了具有针对性和实用性的灾害防治建议，从而可为公路部门制定科学合理的边坡防灾减灾方案提供可靠的信息支持，同时也为该领域的变形监测工作提供了一种新思路.