地铁列车进站过程中活塞风对站台屏蔽门的影响——以杭州地铁为例

董梦雪， 赵帅帅

（杭州万向职业技术学院，杭州 310023）

交通领域是碳排放大户，也是碳减排的重点，其中城市交通的碳排放控制亦备受关注［1］. 在诸多城市交通方式中，地铁以其迅捷、运量大、单位能耗较小和污染小等优点被称作“绿色交通”［2］，但其在运行中也有一些问题亟待解决，如地铁在高速运行中会在隧道内产生活塞风效应，在站台全封闭屏蔽门（以下简称为屏蔽门）内外形成巨大的压力差，可能导致屏蔽门爆裂而出现安全事故. 2019年5月31日下午1时10分，杭州地铁2 号线一辆列车在进站时，站台屏蔽门突然发生炸裂（图1）. 因此，有必要研究活塞风对地铁站台屏蔽门的影响，以保障地铁列车的安全运行.

图1 地铁站台屏蔽门炸裂事故现场Fig.1 Scene of explosion accident of platform screen door

地铁活塞风效应是指列车在隧道中高速运行时带动隧道中的空气高速流动，继而导致隧道内空气压缩或膨胀的现象. 目前，学者们主要从实验测量和数值模拟等两个方面对地铁活塞风效应展开研究. 沈翔等［3］测试了上海地铁车站内活塞风的情况，发现列车进站时活塞风绝大部分进入站台，能对车站内的气流产生巨大影响. 张悦等［4］以广州地铁某站及其中间风井为研究对象，对地铁风道内的风速进行了现场测试，发现出站端活塞风道内的正、负风速最大幅值均低于进站端，且相比于进出站端活塞风井，中间风井内风道的风速更高. 然而，实验测量得到的数据较少，较难全面反映地铁活塞风的流动全貌及细节. 因此，数值模拟的方法逐渐成为研究地铁活塞风的重要手段. 任明亮等［5］采用SES与CFD商业计算软件分析了活塞风的形成机制及其作用于地铁隧道内的空气流动特性和影响规律，并与现场实测结果进行了比较，发现数值计算结果与实验结果具有较好的一致性. 徐驰等［6］采用模拟分析的方法对比了不同方案下的地铁活塞效应，得出了提高区间隧道空气品质的方法. González等［7］以两个相邻车站之间的地铁线路为研究对象，建立了一个三维计算模型，分析了活塞效应对地铁隧道纵向通风系统的影响. Juraeva等［8］利用ANSYS CFX软件求解雷诺平均Navier-Stokes方程，对某地铁隧道内的三维定常气流进行了分析，建立了该模型地铁隧道的通风系统. 在活塞风对屏蔽门影响的研究中，学者们也常采用数值模拟的方法. 袁誉钊等［9］构建两车、两车站、三区间隧道的地铁隧道模型，利用滑移网格技术仿真模拟列车在隧道运行时引起的活塞风速度与压力，并提取所研究车站屏蔽门区域所受活塞风的压力值. 何磊等［10］则基于有限体积法建立了地铁车站三维静态数值计算模型，分别分析了单、双两种活塞通风条件下，不同活塞风速、阻塞比、滑动门位置对滑动门所受风压的变化规律. 杨伟超等［11］采用有限体积法模拟列车在区间隧道内运行过程，发现屏蔽门压力变化主要是由列车的有压科特湍流和区间隧道内压力波两方面因素决定. 其中有压科特湍流是主要影响因素，屏蔽门压力与阻塞比和列车速度的平方呈正比；增加活塞风井面积、打开活塞风阀有利于降低屏蔽门压力.

现有的研究常以匀速运动的地铁列车为对象，研究其运行过程中产生的活塞风，较少考虑变速运行地铁列车的活塞风效应. 而现实中屏蔽门常设置于地铁站，地铁列车达到或离开地铁站时是处于减速或加速运动状态，故应重点关注这两种状态下活塞风对屏蔽门的影响. 在这两种车辆运行状态下，地铁列车进站时初始速度高，其活塞风效应更为显著. 为此，采用现场实验与数值模拟相结合的方法，研究列车进站过程中屏蔽门表面压力的时变特性，讨论车辆进站过程中活塞风对屏蔽门的影响，并分析其潜在的破损风险.

1 理论基础

1.1 控制方程

地铁活塞风属于流体运动的范畴，流体运动是一种连续介质的运动，属于机械运动的范畴，并遵循物质运动的普遍规律. 由质量守恒定律建立的连续性方程、由动量定律建立的动量方程和由能量守恒定律建立能量方程构成了流体动力学控制方程. 其中连续性方程和动量方程如下所示［12］：

根据质量守恒定律，流入和流出控制体的流体质量差等于该时段内控制体中的流体质量变化量，即可得到流体流动的连续性方程：

式中：u为流体速度；ρ为流体密度；t为时间；x为距离.

根据动量定律，流体流动过程动量守恒的表达式写成张量形式为：

式中：f为质量力；σij为应力张量分量.

1.2 动网格技术

针对地铁列车的运动过程，目前大部分研究采用动网格技术对其进行数值计算［13-15］. 动网格技术可用于模拟由流体域边界刚性运动或者边界变形引起的流体域形状随时间变化的流动问题. 边界运动可以分为两种，即预先指定的运动（如线速度或者角速度随时间的变化）和非预先指定的运动（其后续运动由当前时间步的解确定）.

对于边界移动的任意控制体积V上的任意标量Φ的守恒型动网格流场，计算方程可以表示为：

式（3）中时间导数项可以写成一阶向后差分形式：

式中：n和n+1分别为当前及下一步的时间层；第n+1个时间步控制体可由下式解得：

式中：nf为控制体面数；A→j为第j个面的法向矢量；控制体积面上的点积可由下式解得：

式中：δVj为控制体上的面j在时间步Δt内扫出的体积.

2 计算模型与参数设置

2.1 几何模型

地铁列车进站过程的实验数据取自2021 年3 月19 日杭州市地铁1 号线文泽路地铁站，故以该站为对象进行数值建模. 该站为地下二层岛式站台（即站台位于上下行车线路之间），为了提升计算精度且节约计算成本，对站台、隧道及地铁列车进行了简化建模（图2）.

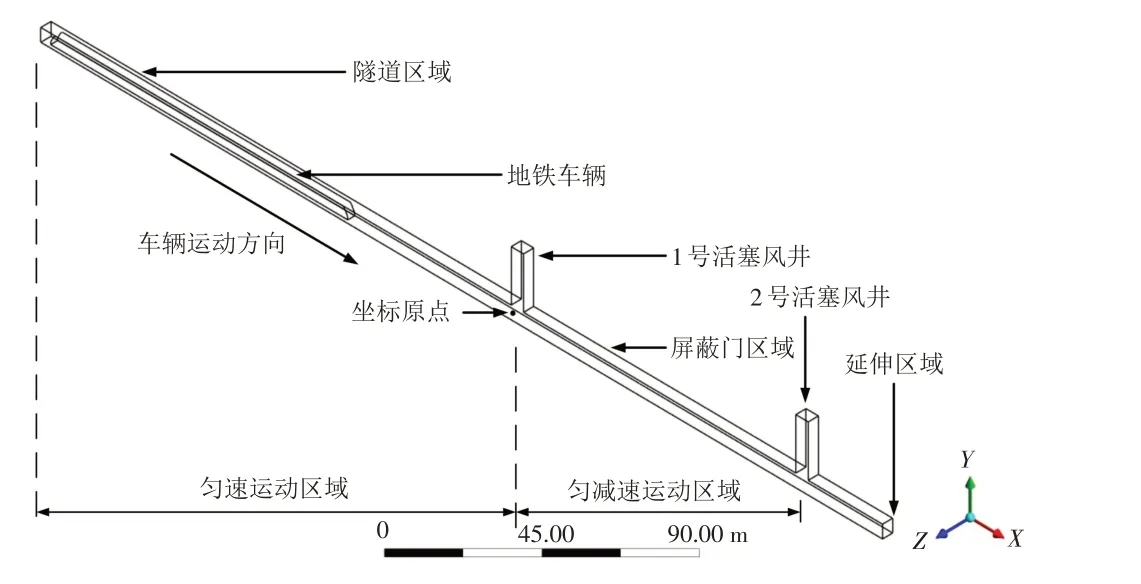
图2 数值计算模型Fig.2 Numerical simulation model

杭州市地铁1 号线使用6 节编组的B型地铁车辆，列车长宽高分别为120 m、2.8 m和3.8 m. 为了更贴近实际运行状态，以区间隧道与站台屏蔽门连接处为界，进站过程被分为匀速运动阶段与匀减速运动阶段. 上述两阶段所处区域如图2，匀速运动区域长150 m，匀减速运动区域长120 m，延伸区域长30 m. 活塞风井位于屏蔽门区域前后端，长宽高分别为5、4.1 m和20 m. 隧道高5.06 m，宽4.1 m；屏蔽门区域长120 m.

2.2 数值方法

几何模型计算域中的流体为空气，本文采用有限体积法离散控制方程，采用SSTk-ω模型模拟复杂边界层分离流动［15］. 压力与速度耦合采用SIMPLEC算法，并使用QUICK格式降低假耗散的影响. 计算域内所有壁面均为无滑移壁面（标准壁面函数），进出口边界条件均采用标准大气压（压力参考0点）. 本文采用四面体非结构化网格划分计算域，经网格无关性计算后，采用360万网格数进行计算.

2.3 动态参数获取与设置

为保证活塞风数值计算的准确性，列车进站过程的速度参数由现场实验获得. 经多组平行实验测量，列车进入站前的平均速度为13.33 m/s；列车减速运动持续时间约18 s，经过拟合后得到加速度为-0.74 m/s2. 根据实验获得的动态参数，使用ANSYS Fluent 15软件中弹簧近似法和局部重构法进行动网格计算［16］，在弹簧近似法中弹性系数设为0.5，节点松弛因子为0.5，收敛容差为10-5，迭代步数为20；根据实测数据编写Profile文件用于控制列车运动，列车进站前以13.33 m/s的速度进行5 s匀速直线运动，之后以-0.74 m/s2的加速度减速，最终列车停靠在站台. 考虑到列车到站后活塞风并不会马上消退，计算停车后5 s内的活塞风情况，则总计算时长为28 s. 活塞风非定常计算的时间步长为0.001 s，每个时间步长迭代20次.

3 结果与分析

3.1 活塞风非定常流动特性

按计算得到地铁列车进站过程中隧道内活塞风的流动情况，图3为X-Y截面上地铁列车进站过程中活塞风速度分布（其中，t0为计算初始时刻）.

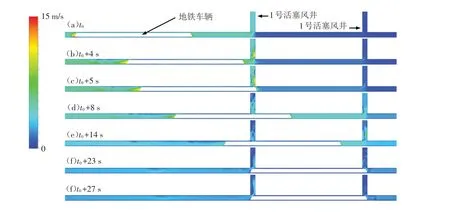
图3 地铁进站过程中活塞风速度分布（X-Y截面）Fig.3 Velocity distribution of piston wind during metro arrival（X-Y section）

由图3可以看出，在t0时刻，列车处于匀速运动阶段且距离站台屏蔽门较远，其运动过程带动了周围空气的运动而产生活塞风，因距离活塞风井较远，对1号和2号活塞风井之间的空气影响有限；在t0+4 s时刻，列车处于匀速运动阶段且运动至1号活塞风井附近，大量活塞风通过1号活塞风离开隧道，虽然两个活塞风井间的空气受其影响而提升了风速，但列车对2号活塞风井内的空气流动影响较小；在t0+5 s、t0+8 s和t0+14 s时刻，列车处于匀减速进站过程，对1号和2号活塞风井之间的空气运动的影响逐渐显现出来，该区间内的空气流速逐渐提升，但对已通过的隧道区域内的空气流动的影响却逐渐较弱；值得注意的是，在列车匀减速进站的过程中，1号活塞风井内的空气流动逐渐减弱而2号活塞风井内的空气流动逐渐增强，这表明不同位置的活塞风井在列车不同进站过程中所发挥的作用是不一样的；在t0+23 s和t0+27 s时刻，列车处于静止状态，周围的活塞风虽减弱但仍处于运动状态，并未像列车一样立刻静止，这表明列车进站过程所引起的活塞风具有滞后性.

3.2 屏蔽门表面压力时变特性

通过对运动特性的分析，活塞风在地铁列车进站过程中表现出强烈的非定常特性. 受其影响，屏蔽门表面压力亦会表现出波动的特征. 为了定量测量屏蔽门表面压力，以图2所示坐标原点为0点，选取距离隧道底部上方2 m处且沿列车运行方向分别为3、6、9、12、15 m共5个屏蔽门近壁面（距离屏蔽门0.1 mm）测压点，以监测列车进站过程中屏蔽门表面压力时变特性. 图4所示为列车进站过程中屏蔽门近壁面测压点的压力变化. 从图中可以看出，压力点的压力有非常明显的波动，并整体表现为x越小（即越靠近1号活塞风井）压力波动的幅值越大. 当列车运行于区间隧道时（0～5 s），各监测点处压力呈现出3个波峰和2个波谷的变化特征，最大值达到201 Pa；相较于匀速运行阶段，列车于减速进站阶段（5～23 s）所引起的屏蔽门表面压力变化更为剧烈；在列车通过1号活塞风井后（6 s），屏蔽门表面压力达到最大值（1188 Pa），这是由于列车通过1号活塞风井后运动至该处并对周围空气挤压；但随后该压力急速下降至-266 Pa，并在之后的运行时间内，屏蔽门表面压力反复振荡，最后趋于稳定.

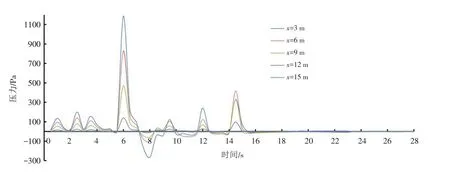
图4 列车进站过程中屏蔽门近壁面测压点压力变化Fig.4 Pressure change of the measuring point near the wall of the screen door during subway train entry

为探究压力振荡的原因，重点观察了1号活塞风井处的流线（图5）. 在列车尚未接近站台轨行区时（t0），活塞风顺畅地从1号活塞风井流出隧道；当列车接近站台轨行区时（t0+4 s），1号活塞风井内出现了回流区，且该区域随着列车逼近1号活塞风井而逐渐扩大（t0+5 s），在该回流区的作用下，屏蔽门表面压力呈现出波动性（图4）；当车头刚通过1号活塞风井时，列车仍具有较高速度且其周围空间相对狭小，导致屏蔽门表面压力出现最大值（图4）；随着列车通过1号活塞风井（t0+8 s和t0+14 s），原有的回流区分裂为两个，但此时列车行驶速较低，引起的活塞风明显减弱，活塞风与回流区相互叠加导致9～16 s内压力波峰和波谷的产生（图4）；列车停于站台轨行区时（t0+27 s），1号活塞风井内的回流区仍未消失，这也导致列车虽停止运行但屏蔽门表面仍有压力现象的发生.

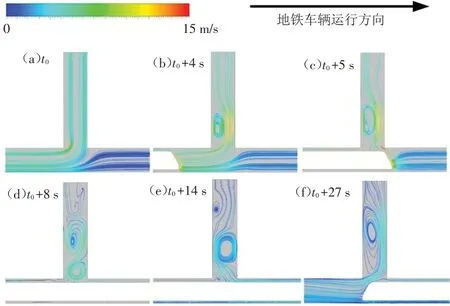
图5 1号活塞风井处流线Fig.5 Flow line in No.1 piston air shaft

4 结论

本文对车辆进站过程中活塞风对地铁站台屏蔽门的影响开展了研究，通过现场实验的方法测量得到地铁列车进站过程的速度参数，基于此数据采用动网格方法数值模拟了列车进站过程中活塞风的非定常流动特性，并根据计算结果得到了屏蔽门表面压力时变特性. 研究发现，在地铁列车进站过程中，活塞风井对活塞风的疏导作用与列车位置相关，距离车头位置越近的活塞风井对活塞风的疏导作用越大；列车进站过程会引起屏蔽门表面压力变化，在车头通过第一个活塞风井后达到峰值，此时站台屏蔽门破损风险较大，且越靠近该活塞风井的屏蔽门表面压力波动幅值越大；在列车进站过程中，活塞风井内存在着回流区并不断地发展演化，并与列车对空气挤压产生的活塞风相互叠加，导致站台屏蔽门表面压力出现反复振荡的特性.