基于局部均值分解和PSO-RVM-ARIMA模型的基坑变形预测研究
2021-11-22王飞
王 飞
(陕西铁路工程职业技术学院,陕西渭南 714000)
近年,我国市政交通行业得以快速发展,并显著增加了地下空间的开发利用,其中,形成了规模较大的基坑工程;由于基坑施工具有空间立体特征,加之地质条件限制,使得基坑变形对其安全施工具有直接影响,因此,开展基坑变形预测研究具有重要的工程价值[1-3]. 目前,已有相关学者开展了基坑变形预测研究,如袁志明等[4]、李柏佚等[5]在考虑基坑邻近监测点间的相互影响基础上,构建了监测点间的关联预测模型;苏秀婷等[6]利用有限元法实现了基坑预测分析;王雪妮和韩国锋[7]则利用极限学习机实现了基坑变形预测.上述分析为基坑变形规律研究提供了相应研究思路,也取得了一定研究成果,但上述研究均未考虑基坑变形数据中含有的误差信息影响,也未涉及相关向量机的应用研究,因此,仍需进一步拓展基坑变形预测方法研究. 受监测环境影响,基坑变形数据往往含有一定的误差信息,对预测结果具有一定影响,因此,在基坑变形预测前,有必要先进行变形数据的信息分解处理;同时,单一模型也难以完全刻画基坑的非线性变形特征,进而开展基坑变形的组合预测显得十分必要. 本研究以海之韵站基坑工程为实例背景,先利用优化局部均值分解实现基坑变形数据的趋势项和随机项分解,再利用优化相关向量机和ARIMA模型实现趋势项和随机项的组合预测,以掌握基坑变形的发展规律,为其安全施工提供一定的理论指导.
1 基本原理
按照论文思路,分析过程主要为:先利用局部均值分解(Local Mean Decomposition,LMD)处理基坑变形信息,即将基坑变形数据分解为趋势项和随机项;再利用优化相关向量机(Relevance Vector Machine,RVM)和ARIMA模型构建基坑变形的组合预测模型.
1.1 LMD模型的信息分解过程
LMD模型是一种新型自适应的非平稳信号处理方法,可通过信息分解处理,得到一个特征变形分量,以实现原始信号的完整时频划分,对基坑变形数据的分解处理具有较强的适用性[8-10]. 结合LMD模型的基本原理,可将其分解过程表示为:

式中:x(t)为基坑变形数据;q为趋势项的分解层数;PFi(t)为趋势项分解信号;u(t)为误差项分解信号.
在LMD模型的信息分解处理过程中,由于信号左右两端点并非极值点,易造成趋势项分解信号的内部失真,影响信息分解效果,因此,对端点信号的优化处理显得格外重要. 为合理解决该问题,I-LMD模型应运而生,其利用最小二乘法实现端点信号的极值处理,以保证分解效果.
同时,鉴于信噪比(SNR)能有效评价变形数据的信息分解效果,进而以其为评价指标,进行基坑变形数据信息分解效果评价,评价规则为:SNR值越大,基坑变形数据的信息分解效果相对越优;反之,信息分解效果相对越差.
1.2 变形预测流程
据相关文献[11-16]的研究成果,单一预测模型难以完全刻画基坑变形的非线性特征,组合预测思路具有相对更强的适用性;同时,由于RVM模型与ARIMA模型具有较强的非线性预测能力和误差修正能力,因此,利用两者构建基坑变形组合预测模型. 组合预测流程为:先利用RVM模型进行趋势项变形预测,且为保证RVM 模型的预测效果,利用粒子群算法(Particle Swarm Optimization,PSO)进行RVM 模型的参数优化处理;在趋势项预测基础上,将趋势项预测误差与随机项叠加,组成新的误差随机项,再利用ARIMA模型对其进行弱化处理;将趋势项预测结果和误差随机项预测结果相加,即为基坑变形数据的组合预测结果.
1)PSO-RVM模型. RVM模型是一种新型监督学习方法,由于其不受Mercer定理约束,使得其具有较优的预测能力;在RVM模型的应用过程中,若训练样本为{xi,ti} ,则其预测过程为:

式中:N为样本数;K(x,xi)为核函数;wi为权重向量;zi为噪声;wo为偏差.
鉴于RVM模型已广泛应用于岩土领域[17-21],限于篇幅,不再赘述其基本原理;但是,RVM模型的应用过程存在一定不足,如核函数类型相对较多,各类核函数的适用性存在一定差异;学习因子对预测过程的收敛速率具有直接影响,易造成预测结果陷入局部极值. 为保证预测精度,需对上述两参数进行优化处理,且考虑到PSO算法具有较强的全局优化能力,进而利用其实现RVM模型的参数优化处理,具体优化处理流程为:
①参数初始化. 初始化粒子群的基础参数,如种群数设置为500;维数设置为2,分别代表核函数和学习因子参数;迭代次数限值设置为600.
②迭代寻优. 以预测误差的绝对值为适宜度函数,先计算各粒子的初始适宜度值,选取最佳者作为初始全局适宜度值;其次,改变粒子位置和速度,进行迭代寻优,并对比粒子与全局的适宜度值,实现全局适宜度值的更新,以完成迭代寻优,直至满足期望或达到迭代次数限值.
③参数输出. 当完成迭代寻优后,最优适宜度值条件下对应的核函数和学习因子参数即为寻优参数,将其输出,即完成RVM模型的参数优化处理.
2)ARIMA模型. ARIMA模型具有较强的误差弱化能力,已被广泛应用,因此,利用其实现误差随机项的弱化预测;结合其基本原理,将其修正过程表示为:

式中:Rt为误差弱化值;p、q为回归阶次;rt-m为对应节点处的误差值;φm为自回归参数;θj为滑动参数;at-j为对应t-j节点处的白噪声;at为对应t节点处的白噪声.
2 实例分析
2.1 工程概况
海之韵站隶属大连二号线,具双层岛式结构,近似呈东西走向,中心里程为DK0+274 m,覆土厚度约3 m[13].据现场勘察成果,区内第四系地层主要为人工堆积层、海积土层和洪积层,岩性以粉质黏土、粉砂等为主,工程性质相对略差;下覆基岩以震旦系长岭子组为主,岩性为板岩,主要矿物成分为石英、云母,遇水易软化,属极软岩,较破碎.
由于车站基坑开挖具空间立体特征,加之周边地层岩性相对较差,因此,为切实保证基坑施工安全,参照规范要求,对其进行了沉降监测,监测点沿基坑周边布置,共计布设了25个监测点,其中,X1~X5监测点的数据完整性相对较好,因此,以其为数据来源,开展基坑变形预测研究;在监测过程中,监测频率为1 次/d,共计得到40期的变形监测成果如表1所示.
2.2 变形预测研究
据论文分析流程,变形预测过程共计可分为两个阶段,即:变形数据的信息分解和预测结果分析,将两者的具体分析结果详述如下:
2.2.1 变形数据的信息分解处理 在基坑变形数据的信息分解过程中,为充分验证LMD模型的分解效果,将该过程划分为两步骤,其一,是将LMD模型与若干db小波和sym小波进行数据分解效果的对比研究,以佐证LMD模型相较传统小波分解在基坑变形数据信息分解方面具有更好的适用性;其二,是对比LMD模型优化前后的分解效果,即对比LMD模型和I-LMD模型的信息分解效果均进行统计分析,以验证其优化处理方法的有效性.
首先,通过计算,得到不同小波及LMD模型的信息分解结果如表2所示. 对比三类模型的分解效果,得LMD模型的信噪比相对最大,其值为34.11,其次是sym小波,其信噪比均值为29.55,而db小波的信噪比相对最小,均值为28.79. 因此,得出LMD模型相较两种小波去噪具有更优的分解效果,充分验证了其在基坑变形数据信息分解中的适用性.

表2 不同信息分解方法的效果统计Tab.2 Effect statistics of different information decomposition methods
其次,对LMD 模型进行优化处理,得其优化前后的预测结果如图1所示. 据图1,I-LMD模型的信噪比明显大于LMD模型的信噪比,其信噪比值已达36.24,充分说明对LMD模型的优化处理能有效提高分解效果.

图1 LMD模型优化前后的分解效果对比Fig.1 Comparison of decomposition effects before and after LMD model optimization
综上所述,在基坑变形数据的信息分解过程中,LMD模型相较传统小波去噪具有更优的分解效果,且通过优化处理能进一步提高其分解效果,因此,利用I-LMD模型实现基坑变形数据的信息分解是可行的.
2.2.2 预测结果分析 在前述基坑变形数据信息分解基础上,再开展变形预测分析. 值得指出的是,限于篇幅,难以对所有监测点的预测流程均进行详述,因此,选择X1 监测点为例,详述其各阶段的预测效果,且在预测过程中,1~35 周期数据为训练样本,36~40 周期数据为验证样本.
首先,利用PSO-RVM 模型开展X1 监测点的趋势项预测,且为验证PSO 算法的优化效果,对趋势项优化前后的预测结果均进行统计,结果如表3所示. 在相应验证节点处,PSO-RVM模型较RVM模型具有更小的相对误差,且前者平均相对误差为2.14%,也小于后者的平均相对误差2.22%,说明通过PSO算法的优化处理,能有效提高RVM模型的预测效果.

表3 X1监测点的趋势项预测结果Tab.3 Trend term prediction results of X1 monitoring site
其次,利用ARIMA模型对X1监测点的误差随机项进行弱化预测,以达到提高预测精度的目的,经计算,得X1 监测点经弱化预测后的结果如表4所示. 在X1 监测点的最终预测结果中,相对误差间于1.88%~2.03%,平均相对误差为1.96%,相较趋势项预测结果,预测精度具有一定提高,验证了ARIMA模型的误差弱化效果,且初步验证了该文预测模型具有较优的预测精度.
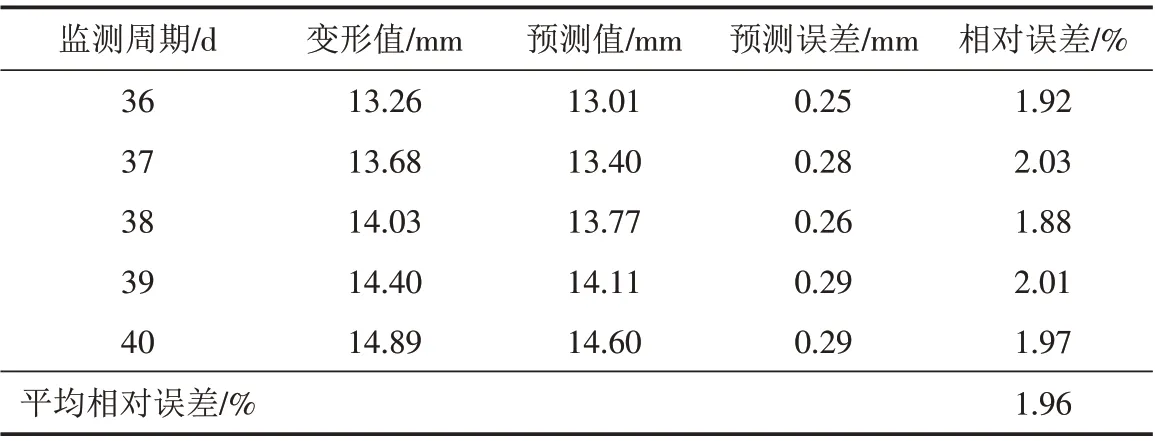
表4 X1监测点的最终预测结果Tab.4 Final prediction results of X1 monitoring site
为进一步对比各阶段的预测效果,再以X1监测点为例,设置5个模型,通过对比分析,评价论文构建思路的合理性,并将模型设置如下:
模型1:RVM模型.
模型2:LMD-RVM模型.
模型3:ILMD-RVM模型.
模型4:ILMD-PSO-RVM模型.
模型5:ILMD-PSO-RVM-ARIMA模型.
经统计,得X1 监测点在不同模型条件下的预测结果如图2 所示. 在数据分解和预测过程中,随优化深入,预测结果的平均相对误差值趋于减小趋势,且以模型5具有相对最优的预测效果,验证了各类优化处理方法的有效性及该文预测模型的合理性.
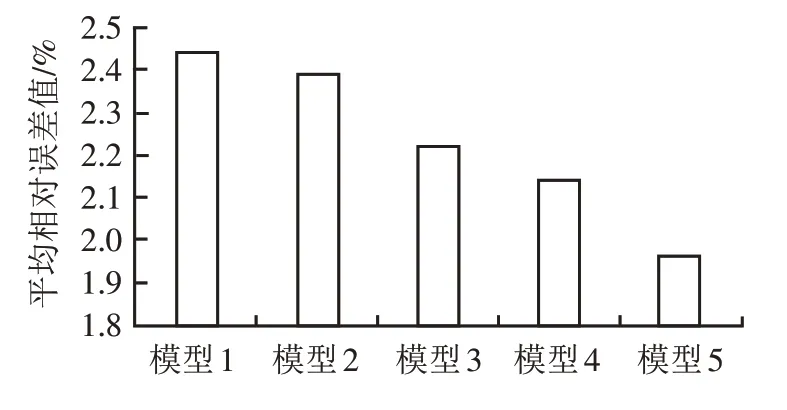
图2 不同模型条件下的预测结果Fig.2 Prediction results under different model conditions
最后,对其余监测点进行类似预测,并进一步对X1监测点进行外推预测,得各监测点的预测结果如表5所示. 在五个监测点的预测结果中,平均相对误差间于1.89%~2.02%,不仅变化范围较小,且均在2%左右波动,说明该文预测模型不仅具有较高的预测精度,还具有较优的稳定性,验证其适用于基坑变形预测. 通过外推预测,得五个监测点的变形仍会进一步增加,但增加速率偏小,说明基坑变形趋于稳定方向发展.
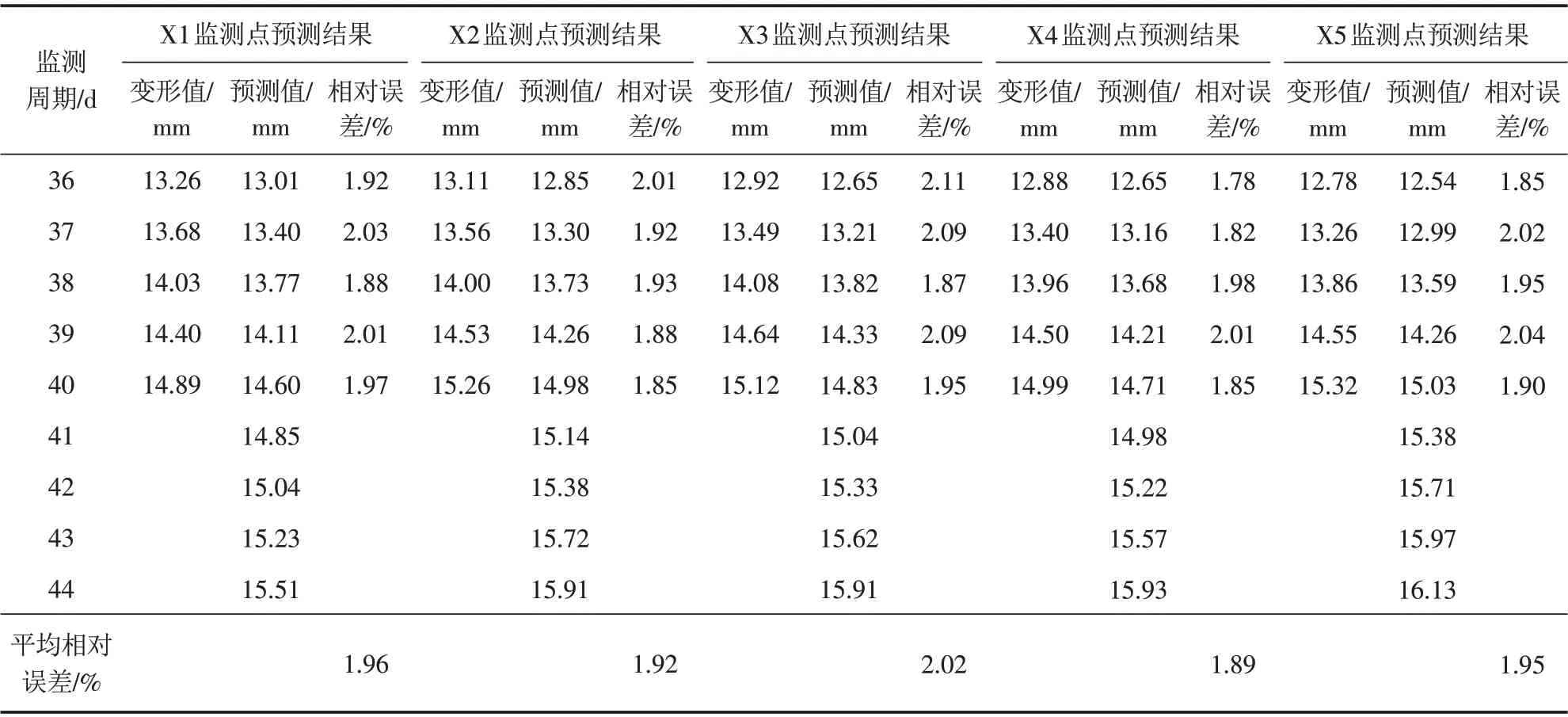
表5 各监测点的最终变形预测结果Tab.5 Final deformation prediction results of each monitoring site
综上所述,通过对海之韵站基坑的变形预测研究,得本文预测模型在基坑变形预测中具有较好的适用性,不仅具有较高的预测精度,还具较优的稳定性;同时,通过外推预测,基坑变形虽会进一步增加,但增加速率较小,变形趋于稳定性方向发展.
3 结论
通过I-LMD模型和PSO-RVM-ARIMA模型在海之韵站基坑变形预测中的应用研究,主要得出如下结论:
1)受监测环境等因素影响,基坑变形数据会含有一定误差信息,LMD模型能有效实现其信息分解处理,较传统小波去噪的优越性明显,且通过优化处理能进一步提高其分解效果,验证了I-LMD模型在基坑变形数据信息分解处理中的适用性.
2)通过PSO-RVM 模型和ARIMA 模型的组合预测,合理实现了基坑变形的高精度预测,验证了本文预测思路在基坑变形预测中的适用性,且通过外推预测,基坑变形趋于稳定方向发展.
