交叉索布置方式对多塔斜拉桥力学性能的影响

2021-11-22柴生波张瑞琳王秀兰

科学技术与工程 2021年30期

柴生波，张瑞琳，王秀兰

(西安科技大学土木工程学院，西安 710054)

近年来，跨越海峡、山谷等地形的交通需求日益增长，对桥梁跨越能力的要求不断提高[1]，多塔斜拉桥在经济及技术方面的优势使其成为极具竞争力的结构方案[2]。但多塔斜拉桥中塔缺少锚索的有效约束，结构刚度远小于两塔斜拉桥，荷载作用下的结构变形显著增大。对于多塔斜拉桥在恒载作用下的变形，可通过调整拉索张拉力、设置预拱度等方法控制[3]。为了减小活载下的结构变形，一般采用增大桥塔或主梁刚度、增设加劲索和辅助墩等方案[4]，而2017年建成的昆斯费里大桥首次采用主跨设置交叉索的方案来提高结构刚度[5]。中国在建的安九铁路鳊鱼洲长江大桥(主跨672 m)为世界首座采用交叉索方案的两塔斜拉桥，设置交叉索有效提升了结构性能[6]。交叉索方案与增设加劲索、增大塔梁刚度的方案相比，既减小了长索下垂效应，又避免了建造大型础[7]，且抗震性能更好[8]。增设辅助墩虽可增大结构刚度，但会增大塔底和主梁的弯矩[9]。

Gimsing等[10]最早对交叉索的作用原理进行了定性论述：当中塔塔顶受到顺桥向不平衡力作用时，梁重在交叉索中重新分配，从而为中塔提供了有效的纵向约束。为明确交叉索的作用机理，Chai等[11]推导了交叉索对中塔的纵向约束刚度，提出了交叉索多塔斜拉桥变形的简化计算方法；邬晓光等[12]在计算交叉索对中塔的约束刚度时，考虑了塔梁刚度的影响。理论研究表明交叉索的长度、设置角度及交叉区域等布置参数影响着交叉索对中塔的约束刚度。同时交叉索多塔斜拉桥的设计还需要确定交叉索的张拉力、数量等参数。一些学者对此开展相关研究，昆斯费里大桥主跨设置6对交叉索，交叉索对称布置于主跨中央，交叉区域为主跨长度的25%[13]。安九铁路长江大桥主跨设置7对关于跨中对称的交叉索[14]。Arellano等[15]基于交叉索的作用机理，在交叉拉索所承担的梁重相同的条件下，通过遗传算法计算了交叉区域的最优长度。为最小化昆斯费里大桥拉索用钢量，Baldomir等[16]提出将每根索的面积设为变量的优化设计方法；Clid等[17]则同时考虑索的锚固位置、数量、张拉力为变量，通过改进遗传算法对拉索布置进行优化。

上述研究和工程实践均证明设置交叉索可提高斜拉桥的刚度、改善结构力学性能。但是，近年来新建主跨设交叉索的斜拉桥均采用交叉索的跨中对称布置，而交叉索的长度、倾角及交叉区域等布置参数影响交叉索对中塔的约束效果，进而影响结构的静动力性能。因此，为研究合理的交叉索布置方式，在现有交叉索布置方式的基础上，现提出交叉索的间隔布置、非对称布置两种新的布置方式，建立交叉索多塔斜拉桥有限元模型，与现有的交叉索布置方式对比，分析间隔布置、非对称布置对结构刚度、受力及动力特性的影响，以期为该类结构的设计提供参考。

1 交叉索布置方式

交叉索可为多塔斜拉桥中塔提供有效约束，从而提高了结构的整体刚度。交叉索对中塔的约束效果受交叉索的长度、倾角及交叉区域等布置参数影响，改变交叉索布置方式，布置参数随之改变。而现有采用交叉索方案的斜拉桥，交叉索集中设置于跨中，且关于跨中对称，如图1所示。

图1 交叉索的现有布置方式Fig.1 Existing arrangement of crossed cables

为研究合理的交叉索布置方式，在交叉索现有的对称布置基础上，提出两种新的交叉索布置方式：①交叉索间隔普通斜拉索进行设置；②交叉索区域向主跨边塔侧偏移的非对称布置。以主跨设置6对交叉索的某多塔斜拉桥为例，取其中一个主跨说明交叉索间隔布置及非对称布置。

1.1 交叉索间隔布置

现有的交叉索布置方式是将交叉索对称设置于主跨中央，交叉区域仅布置相互交叉的拉索。区别于现有的交叉索布置方式，交叉索间隔布置是将交叉索与普通斜拉索交替设置，即交叉索间隔普通斜拉索进行布置，交叉区域设置有交叉索和普通斜拉索。间隔布置与现有的交叉索布置方式相比，两者均关于主跨中央对称，但间隔布置的交叉区域更大。如图2所示，交叉索分别间隔1根、2根斜拉索。

图2 交叉索间隔布置Fig.2 Spacing arrangement of crossed cables

1.2 交叉索非对称布置

交叉索的非对称布置是将交叉区域设置于主跨偏边塔一侧，而现有交叉索布置的交叉区域则位于主跨中央。主跨采用交叉索的非对称布置时，主跨两侧的索面不对称，而对于采用现有交叉索布置方式的主跨，其索面则关于跨中对称。交叉索的非对称布置如图3所示，其交叉区域长度与现有的交叉索布置相同。

图3 交叉索非对称布置Fig.3 Asymmetrical arrangement of crossed cables

2 有限元分析

为研究所提出的交叉索间隔布置、非对称布置方式对多塔斜拉桥整体力学性能的影响，建立主跨设交叉索的多塔斜拉桥有限元模型，通过与现有的布置方式对比，分析交叉索非对称布置、间隔布置对多塔斜拉桥刚度、动力特性和结构受力的影响。

2.1 方案及参数

2.1.1 现有交叉索布置方案

昆斯费里大桥为首座采用交叉索方案的斜拉桥，交叉索关于主跨中心对称布置，主跨交叉索设置细节如图4所示[13]。参照已建成的昆斯费里大桥，拟定跨径布置为[325+(n-1)×650+325] m的交叉索三塔至五塔斜拉桥参数，其中n为桥塔的数量。每个主跨设置24对斜拉索，采用双索面，跨中的6对拉索为交叉索。交叉索采用现有的跨中对称布置，全桥立面布置如图5所示。主梁为钢箱梁，横断面布置如图6所示。桥塔为变截面独塔形式，桥塔高度为200 m，塔底、塔顶的截面尺寸如图7所示。主梁、桥塔、辅助墩截面及材料特性如表1所示。拉索抗拉强度为1 860 MPa，弹性模量为195 GPa。斜拉索的编号由短索向长索递增，编号范围为1#～24#，其中交叉索由来自主跨左侧桥塔的19#～24#索与来自主跨右侧桥塔的24#～19#索依次交叉形成。交叉的拉索编号如表2所示，斜拉索的横截面积如表3所示。斜拉桥采用(漂浮+中塔纵向约束索)体系，梁端及边墩(辅助墩)仅约束竖向，中塔处设置两根关于中塔对称的塔梁纵向约束索，其横截面积为0.011 m2、长度为8 m。

图4 昆斯费里大桥主跨交叉索布置[13]Fig.4 Arrangement of crossed cables on the main span of Queensferry Bridge[13]

图5 现有的交叉索多塔斜拉桥立面布置图(n=3,4,5)Fig.5 Side view of the existing multi-tower cable-stayed bridge with crossed-cables (n=3,4,5)

图6 主梁横断面Fig.6 Cross-section of girder

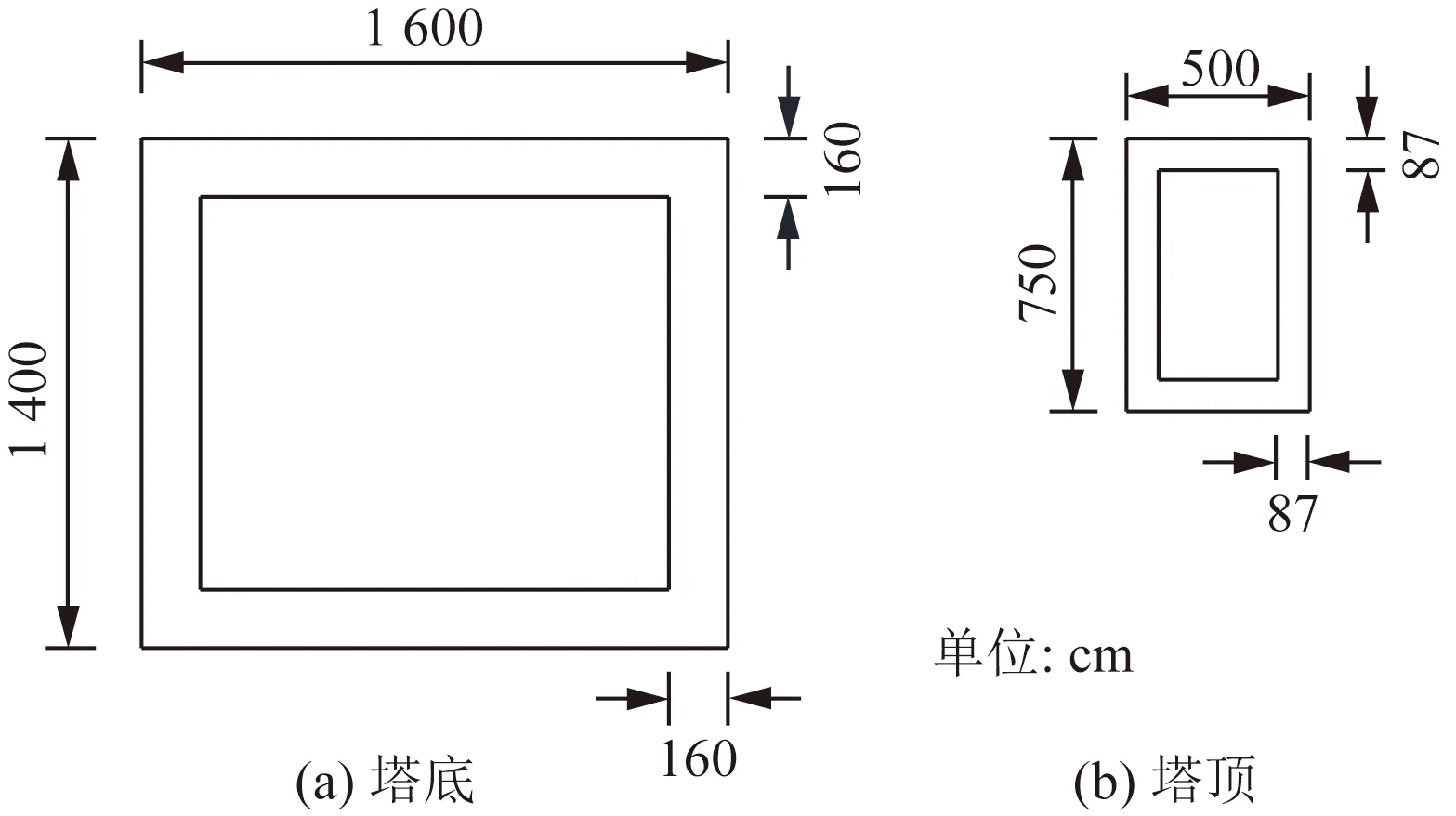
图7 桥塔塔顶、塔底截面尺寸Fig.7 Section of the top and bottom of the tower

2.1.2 交叉索间隔布置方案

表1 结构特性说明Table 1 Structural characteristics

表2 相互交叉的拉索编号Table 2 Serial number of cables crossing each other

表3 拉索横截面积Table 3 Cross sectional area of cable

在主跨拉索索距、交叉索数量及拉索用钢量不变的条件下，以现有交叉索布置为基础，将主跨的23#、24#索向远离跨中的方向移动形成新的交叉索，交叉索分别间隔1根、2根普通斜拉索(除跨中两对交叉索)，交叉的拉索编号如表2所示。为保证交叉索间隔布置方案的主跨拉索用钢量与现有的交叉索布置方案相同，调整间隔布置方案的交叉索面积，调整结果如表4所示。主跨交叉索间隔1根拉索设置的多塔斜拉桥立面布置如图8所示。

表4 交叉索面积数据Table 4 Area of crossed cables

图8 间隔1根拉索设置交叉索的多塔斜拉桥立面布置图Fig.8 Side view of one cable spacing between the crossed cables of multi-tower cable-stayed bridge

2.1.3 交叉索非对称布置方案

以现有的交叉索布置为基础，不改变交叉索的间距及主跨布索区域长度，减小主跨上来自边塔的拉索索距、增大来自中塔的拉索索距，交叉索向边塔侧移动57 m，主跨索距调整结果如表5所示。由于四塔斜拉桥关于中跨的纵向中心对称，中跨交叉索采用现有的对称布置。采用非对称布置的交叉索三塔、四塔斜拉桥立面布置如图9和图10所示。

表5 主梁及桥塔索距Table 5 Cable spacing parameters of girder and tower

图9 非对称设置交叉索的三塔斜拉桥立面布置图Fig.9 Side view of asymmetrical arrangement of crossed cables of three-tower cable-stayed bridge

图10 非对称设置交叉索的四塔斜拉桥立面布置图Fig.10 Side view of asymmetrical arrangement of crossed cables of four-tower cable-stayed bridge

2.2 有限元结果及分析

按照上述方案，建立采用现有交叉索布置、间隔布置及非对称布置的交叉索三塔至五塔斜拉桥有限元模型，提取活载作用下的塔顶水平位移、主跨最大下挠、结构竖向基频和桥塔塔底弯矩。桥塔、主梁和桥墩采用梁单元模拟，斜拉索和塔梁纵向约束索分别采用桁架单元、索单元模拟。荷载采用《公路桥涵设计通用规范》(JTG D60—2015)[18]中的公路Ⅰ级荷载，车道数为6，考虑横向折减系数0.55，纵向折减系数0.95，加载方式为影响线加载。

2.2.1 桥塔变形

在公路Ⅰ级荷载作用下，交叉索三塔、四塔、五塔斜拉桥的塔顶最大水平位移如图11所示。

图11 塔顶最大水平位移Fig.11 Maximum deformation on the top of tower

由图11可知，随着桥塔数量的增多，桥塔的塔顶位移逐渐增大。多塔斜拉桥中塔由于缺少锚索的有效约束，中塔的塔顶位移是边塔塔顶位移的2倍以上。与现有的交叉索对称布置相比，交叉索采用间隔布置、非对称布置时，多塔斜拉桥边塔及中塔的塔顶位移均得到了有效减小。交叉索间隔2根拉索布置时，桥塔的塔顶位移较间隔1根拉索时更小。

如图11所示，当交叉索间隔2根拉索布置时，三、四、五塔斜拉桥中塔的塔顶水平位移较现有交叉索布置减小3.9%、6.6%、8.9%；当交叉索采用非对称布置时，三至五塔斜拉桥中塔的塔顶水平位移较采用现有对称布置减小8.2%、8.6%、9.2%。由此可见，随着桥塔数量的增多，与现有交叉索布置相比，采用间隔布置、非对称布置的交叉索对中塔的约束效果逐渐提高。

综上，在交叉索数量、拉索用钢量相同的条件下，与现有交叉索布置相比，间隔布置、非对称布置可明显提高交叉索对中塔的约束刚度，且非对称布置的提高效果最好。

2.2.2 桥塔内力

在汽车荷载作用下，交叉索三塔至五塔斜拉桥桥塔的塔底弯矩最大值如图12所示。

图12 塔底最大弯矩Fig.12 Maximum bending moment at the bottom of tower

由图12可知，在公路Ⅰ级荷载作用下，交叉索三塔至五塔斜拉桥中塔的塔底弯矩最大，较边塔的塔底弯矩大1倍以上。随着桥塔数量的增多，桥塔的塔底弯矩逐渐增大。桥塔数量相同时，塔底弯矩满足：现有布置方案>间隔布置方案>非对称布置方案。当交叉索间隔2根拉索布置时，塔底弯矩较间隔1根拉索时更小。

如图12所示，当交叉索间隔2根拉索布置时，三塔、四塔、五塔斜拉桥中塔的塔底弯矩较现有交叉索布置分别减小2.2%、4.5%、6.6%；当交叉索采用非对称布置时，三塔、四塔、五塔斜拉桥中塔的塔底弯矩较采用现有交叉索布置分别减小5.6%、5.5%、7.7%。

因此，与现有的交叉索布置相比，间隔布置、非对称布置可显著改善多塔斜拉桥中塔的受力，且改善效果随桥塔数量的增多而提高。桥塔数量相同时，非对称布置对中塔受力的改善效果最好。

2.2.3 主梁变形

在汽车荷载作用下，靠近交叉索多塔斜拉桥纵向中心的中间桥跨变形最大，中跨的最大下挠值如图13所示。

由图13可知，当中跨交叉索采用现有的对称布置时，中跨的下挠最大。在公路Ⅰ级荷载作用下，采用现有交叉索布置的三塔至五塔斜拉桥中跨最大下挠为61.9、82.9、96.8 cm，挠跨比分别为L/1050、L/784、L/671，均满足《公路斜拉桥设计细则》(JTG/T D65-01—2007)[19]规定的挠跨比小于L/400的要求。

由此可见，与现有的布置方式相比，多塔斜拉桥采用交叉索间隔布置、非对称布置时，主梁竖向刚度略大。

图13 中跨最大下挠Fig.13 Maximum deflection in the middle span

如图13所示，与现有的交叉索布置相比，多塔斜拉桥采用交叉索的间隔布置、非对称布置时，中跨最大下挠均有所减小。交叉索间隔2根拉索布置时，主梁竖向刚度较间隔1根拉索时更大。当交叉索间隔2根拉索时，三塔至五塔斜拉桥中跨的最大下挠较交叉索采用现有布置时减小0.03%、2.8%、4.9%；当交叉索采用非对称布置时，三塔至五塔斜拉桥中跨的最大下挠较交叉索采用现有布置时减小0.01%、6.6%、3.4%。

2.2.4 竖向基频

交叉索三塔至五塔斜拉桥的竖向基频如图14所示。

图14 竖向基频Fig.14 Vertical fundamental frequency

由图14可知，与现有的交叉索布置相比，采用交叉索间隔布置、非对称布置的多塔斜拉桥竖向基频更大。与间隔1根拉索相比，交叉索间隔2根拉索时，结构的竖弯基频较大。

如图14所示，与现有的交叉索布置相比，当交叉索间隔2根拉索时，三塔至五塔斜拉桥的竖向基频增大了1.4%、2.4%、4.3%；当交叉索采用非对称布置时，三塔至五塔斜拉桥的竖向基频增大了0.7%、1.9%、2.7%。由此可见，与现有的交叉索布置相比，交叉索采用间隔布置及非对称布置可增大结构的竖向刚度。

综合来看，在交叉索数量及拉索用钢量不变的条件下，与现有的对称布置方式相比，交叉索采用间隔布置、非对称布置时，可为中塔提供更加有效的约束，增大结构刚度、减小桥塔受力。同时，与交叉索间隔1根拉索的布置相比，交叉索间隔2根拉索的布置方案对结构力学性能的改善效果更好。

2.2.5 主梁轴力

在汽车荷载作用下，三塔、四塔、五塔斜拉桥的主梁轴力如图15所示，负值代表主梁受压。

图15 主梁轴力Fig.15 Axial force of main girder

由图15可知，交叉索多塔斜拉桥主跨的轴力在跨中处最小，在塔梁相接处最大。主跨轴力：非对称布置>间隔2根索布置>间隔1根索布置>现有布置。采用交叉索非对称布置和间隔布置的主跨轴力较大的原因是：交叉索的长索倾角减小，其索力的水平分量有所增大。对于边跨轴力，采用交叉索非对称布置时轴力最小，采用其余三种布置时轴力稍大且数值相近。