基于声压测量的结构模态参数识别研究

2021-11-22郑佳艳周志祥余忠儒唐俊义邓国军

科学技术与工程 2021年30期

郑佳艳，刘年，周志祥，余忠儒，唐俊义，邓国军

(1.重庆交通大学土木工程学院，重庆 400074； 2.深圳大学土木交通工程学院，深圳 518061)

近年来，土木工程结构的健康监测与诊断技术迅速成为国际学术界和工程界关注的热点[1-4]。在桥梁领域，传统的桥梁健康监测手段通过布置在桥上的振动传感器来获取结构模态参数，进而对结构状态进行评估[5-7]。在实际工程中，由于接触式振动传感的器布设难度高、传感器与结构粘接不紧密而造成的数据噪声过大，导致监测失效的问题也客观存在；另一方面，对于小型结构试件、缩尺模型试件，传感器的附加质量会对结构模态识别造成影响[8]。如何消除传感器附加质量对结构振动的影响目前尚无行之有效的方法，而采用非接触式的传感器对结构的振动特性进行监测是目前学者公认最为行之有效的方法之一。

文献[9-10]采用摄影测量的方法，获取了悬索桥模型的振动位移信息，并在此基础上提取了模型桥的模态参数。但该方法受限于摄像机的硬件参数，其对光照要求高，并且测量时设备抖动也会对测量效果产生很大的影响。声音信号具有非接触、采集方便和处理速度快等优点。从本质上来说，结构振动激发周围介质形成声场辐射出声，声音信号中包含了振动周期信息以及脉冲成分，当结构出现故障时，声音信号中也包含了结构损伤信息。此外，声学故障诊断技术具有如下特点：非接触式测量、设备简单、速度快、信号易于测取、易于发现早期故障、无需事先粘贴传感器、可对移动目标进行在线监测等。陈建新等[11]运用声音传感器远距离获取了行驶车辆的声波数据，并通过Hilbert-Huang变换进行分析，有效地对车型进行了分类。王若平等[12]将经验模态分解(EMD)与梅尔频率倒谱系数(MFCC)相结合，在半消声室中对交通各类车辆笛声进行了分类识别。Prezelj等[13-14]利用麦克风测量了一块薄板的近场声压信号并通过离散Rayleigh积分方法实现了对薄板振型的可视化。Liu等[15]提出一种基于模态的声场反演方法，通过板的振动模态来描述声场。夏茂龙等[16]通过构建结构振动辐射声压与激励之间的频响函数矩阵，成功实现了利用声压辐射信号对一块平面钢板的振动模态识别。张亚建等[17]在实验室利用高精度麦克风获取了小型机械结构在锤击下的声压信号，成功获取了该结构的模态参数，测试结果与数值结果最大误差不超过3%。喻敏等[18]运用有限元耦合间接边界元方法模拟一块大跨度开孔高腹板并进行声辐射分析，证明了结构的辐射声功率以及辐射效率对结构刚度改变的敏感性较高。余忠儒等[19]、Yu等[20]通过建立声固耦合模型并利用有限元对一拉索及其周围的声场进行了模拟，验证了利用声压信号识别索力的有效性。接着，在实验室开展试验研究，分别利用声音传感器和手机麦克风获取了拉索自由振动下产生的声压信号，并成功识别了拉索的张力值。但相关研究仅在低噪声环境下针对小尺度构件开展试验。并且未提出一种有效的且适用于处理强噪声环境下针对大型梁式结构的振动辐射声压信号的分析方法。

综上所述，通过辐射声压信号能够在近场以非接触式的方式有效获取动力参数。但与结构相关的研究中仅针对低噪声环境下的小尺度构件开展了试验，缺乏适用于强噪声环境下大型结构的振动辐射声压信号的分析方法。为探索非接触式声压测量技术在复杂环境下识别桥梁结构模态参数中的应用效果，现在结构大厅利用声音传感器对一跨径为11.2 m的H型钢梁开展动力试验，针对测试环境中包含的大量高频噪声，提出Hilbert-Huang变换二次滤波时频分析方法对非平稳声音进行降噪滤波处理，并对结构模态参数进行提取。不同测试位置的频率测试结果与传统接触式加速度传感器的测试结果接近，并且模态振型吻合度高，验证该方法的有效性与准确性。以期为桥梁健康监测非接触式测量、分析结构振动声压信号提供新的思路。

1 自由声场中声压与结构动力响应

结构在瞬时激励作用下受迫振动会在周围的介质中激发声波形成声辐射。将H型钢梁某截面视为存在于自由声场中的辐射声源，并且将该界面离散为有限个半径为r0的单元面，此时单元面的几何尺寸远小于声波波长，因此可将离散的单元面看作为点声源[21]，如图1所示。对于点声源激发声场中的声压：

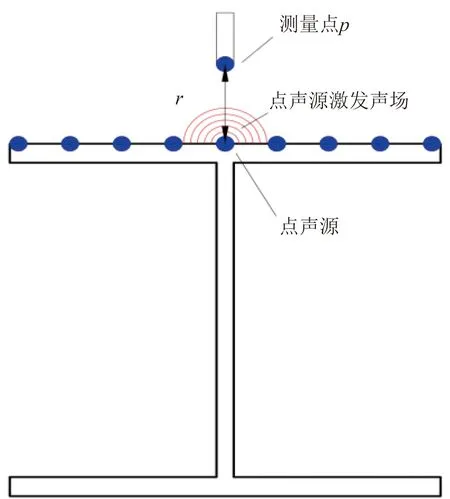
图1 声压辐射图Fig.1 Sound pressure radiation diagram

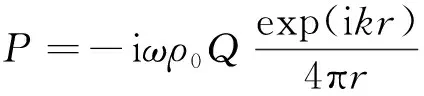
(1)

钢梁受激励自由振动时，点声源向周围介质辐射出声，使结构外一点p的声压发生变化。在结构动力响应中，由钢梁振动导致p点产生的声压可以看作为各阶声压响应的叠加：

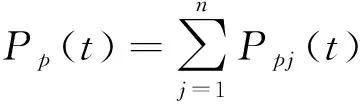
(2)

式(2)中：Pp(t)为t时刻测量点p因钢梁振动产生的声压，Ppj(t)为t时刻p点第j阶振动声压响应。对于有阻尼的H型钢梁结构，其振动表面第j阶径向振速：

Vj(t)=V0exp(iωjt)

(3)

aj(t)=V′j(t)=iωjV0exp(iωjt)

(4)

式中：ωj为结构第j阶固有频率；aj(t)为振动表面第j阶径向振动加速度。结合式(1)～式(3)可得测量点p第j阶声压：

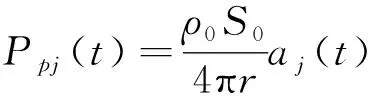
(5)

式(5)表明，当点声源激发的自由声场中的测量点与点声源距离不变时，其第j阶声压大小与点声源振动径向加速度成正比。上述理论构建了点声源自由声场中声压与结构振动响应加速度之间的关系，为后续从声场中针对H型钢梁开展动力特征分析提供了理论支撑。

2 基于Hilbert-Huang变换的时频分析

傅里叶变换要求信号必须是线性平稳的，否则频域分析的结果没有明确的物理意义[22]。由于利用声音传感器接收到的信号为短时平稳信号，当声音时间历程超过40 ms时不再具有平稳性，此时传统的信号分析方法将会失效。

由Huang等[22]提出的经验模态分解(empirical mode decomposition，EMD)方法认为任何复杂信号都由一些不同尺度的固有模态函数组成，并且适用于处理非平稳信号。其目的是将任意非线性非平稳信号分解为n阶固有模态函数(intrinsic mode functions，IMFs)的线性叠加。具体步骤如下。

(1)通过原始信号x(t)的极大值和极小值，拟合出上下包络线，求得其均值m1(t)。令h1(t)=x(t)-m1(t)。若h1(t)的极值点数与零点数相差不超过1，且h1(t)重新拟合的上下包络线任意点均值为0，则令x1(t)=h1(t)称为一阶IMF。

(2)令r1(t)=x1(t)-h1(t)，将r1(t)作为新的原始信号重复步骤(1)直至经验模态分解结束。

基于声音传感器获取的自由声场中结构近场辐射声压信号Pp(t)，将其通过EMD分解为有限个固有模态函数xj(t)和残差rn的叠加。

(6)

将Hilbert变换(HT)应用于上述各阶分量xj(t)中，得

(7)

式(7)中：yj(t)为xj(t)的Hilbert变换；K为柯西主值。yj(t)与xj(t)形成共轭对，dτ表示时间的微分，各阶IMF解析解可以表示为

zj(t)=xj(t)+iyj(t)=Aj(t)eiθj(t)

(8)

(9)

因此，各阶IMF瞬态频率ωj(t)可以表示为

(10)

由此可知，利用EMD分解出来的IMFs通过Hilbert变换分析出的瞬时频率ωj为其瞬时相位θj(t)的微分。

对于强噪声环境中获取的结构辐射声压信号，若直接进行Hilbert-Huang变换(HHT)，原始信号中存在的大量随机噪声信号将会使得瞬时相位线性拟合程度差。文献[23]采用改进的HHT方法，首先将原始信号通过滤波处理再进行时频分析。但该方法在分析低阶IMF时依旧会出现瞬时相位线性程度不佳，瞬时频率不集中的现象。针对上述问题，提出基于HHT的二次滤波时频分析方法对声压信号进行处理分析。该方法围绕有限元计算出的钢梁第3阶固有频率构造切比雪夫Ⅰ型带通滤波器对原始信号进行第一次滤波，通过HHT分析以确定的结构各阶固有频率的分布范围。接着进一步缩小滤波器通带对原始信号进行第二次滤波，最后进行时频分析以达到精确提取结构固有频率的目的，具体分析流程如图2所示。

图2 分析流程Fig.2 Analysis process

3 试验模型及布置

为验证本文所提方法的有效性，在实验室对一根12 m长的H型简支钢梁开展动力试验。为方便支座的布置和保证结构的稳定性，梁的两端分别留出40 cm的悬臂端，计算跨径为11.2 m，H型钢梁规格为HW250×250×9×14/Q235。

采用非接触式的声音传感器垂直放置于钢梁上翼缘表面获取瞬时激励作用下结构自由振动产生的近场辐射声压信号，并通过上述信号处理方法对实测声压信号进行分析，以获取结构的模态参数。同时，在结构相应位置安装加速度传感器以验证利用非接触声压测量技术开展结构动力特征分析的准确性。两种测量方式均设置3个测点：声音传感器S1、S2、S3分别悬空垂直布置于钢梁1/4L、1/2L、3/4L跨处(L为梁的净跨径)，距离上翼缘表面3 cm位置处；加速度传感器C1、C2、C3通过磁性底座分别贴附于钢梁下翼缘表面1/4L、1/2L、3/4L跨处。采用橡胶锤锤击的方式对钢梁表面施加瞬时激励，使钢梁自由振动辐射出声，激励位置位于钢梁5/8L跨处。本文试验测试环境温度为23 ℃，自由声场的介质密度ρ0=1.293 kg/m3，模型布置示意如图3所示，实际布置情况如图4所示。

图3 试验布置示意图Fig.3 The schematic diagram of model arrangement

图4 实验室布置Fig.4 The arrangement in laboratory

4 基于HHT的二次滤波的信号分析

4.1 结构固有频率分布区间识别

钢梁振动辐射出声，此时各测点获取的辐射声压信号如图5所示。从图5中可以看出各测点的声压幅值存在明显差异，并且环境噪声信号贯穿于整个时间历程。在22～30 s的时间范围内可以明显看出原始信号中存在较大且不规律的噪声信号幅值。针对图5实测声压信号，采用基于HHT的二次滤波时频分析方法提取钢梁固有频率，选取S1测点实测声压信号作为说明。

图5 各测点声压信号Fig.5 The sound pressure signal of each measuring point

通过构造切比雪夫Ⅰ型带通滤波器对原始信号进行降噪处理[16]，根据有限元计算出的钢梁第3阶固有频率，首先将滤波器通带范围设置为45～65Hz。经滤波处理后的声压信号经EMD分解为2个IMF和1个残差信号，结果如图6所示。

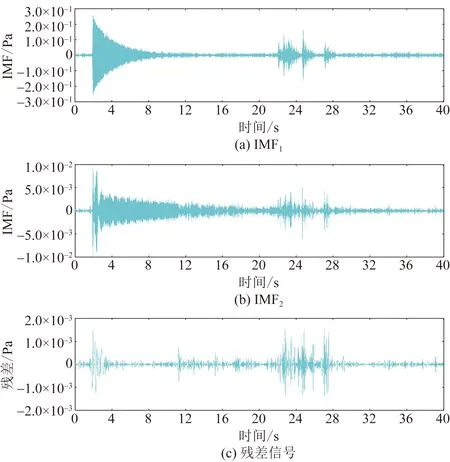
图6 第1次滤波后的EMD分解结果Fig.6 The EMD decomposition results after first filtering

从图6可以看出，原始声压信号经带通滤波并EMD分解后的IMFs从高频到低频依次排列，并且各IMF所包含的频率成分各不相同。将第一阶IMF进行Hilbert变换，其瞬时相位和瞬时频率如图7所示。图7表明，未经滤波的声压信号直接通过HHT分析后，其瞬时相位线性程度差，并且瞬时频率分布杂乱、不集中、无法识别出结构的固有频率。从图7(a)中可以看出，经一次滤波处理后并通过HHT得到的瞬时相位线性程度高、高频噪声少，并且从图7(b)中可以看到，瞬时频率集中于52～60 Hz,但仍无法准确识别出钢梁的第3阶固有频率。同样的，对第2阶IMF以及残差信号进行Hilbert变换，可以识别出结构的第2阶固有频率在范围20～30 Hz。但从图8中可以发现，残差信号的瞬时相位仍然存在线性拟合程度低的情况，瞬时频率分布杂乱，且位于15 Hz以下。上述分析表明，将声音传感器获取的结构辐射声压信号直接通过HHT处理后，由于强噪声的影响，无法有效从瞬时频率结果中识别出结构的前三阶固有频率。但从一次滤波处理后的信号分析结果中可以发现，结构固有频率的分布范围是比较容易识别的，这也为信号的二次滤波提供了方向。

图7 第一次滤波后IMF1瞬时相位、频率Fig.7 IMF1 instantaneous phase and frequency after the first filtering

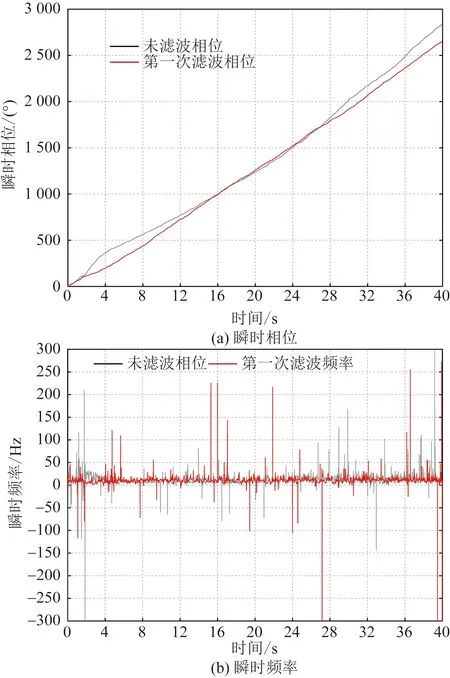
图8 第一次滤波后残差瞬时相位、频率Fig.8 Residual instantaneous phase and frequency after first filtering

4.2 基于二次滤波的固有频率精确提取

为此，提出了基于HHT的二次滤波时频分析方法，在获取结构固有频率分布区间的基础上，进一步缩小信号带通范围。分别构造通带范围为52～60 Hz、20～30 Hz的带通滤波器对原始信号进行二次滤波处理再进行HHT。按照图2所给信号处理流程对二次滤波后的信号进行EMD分解，并求取其瞬时频率，如图9所示。

图9 第二次滤波后第1、2阶瞬时频率Fig.9 The first and second instantaneous frequencies after the second filtering

从图9中可以看出，辐射声压信号经二次滤波处理后，其瞬时频率结果较一次滤波处理的结果更加平滑与集中。这是因为随着带通范围的缩小，大部分的环境噪声已被滤除，此时的信号更能真实反映出结构的振动状态。从图9中可以发现，二次滤波后的1阶和2阶瞬时频率结果分别稳定在55.6、26.6 Hz。通过均值拟合方式可以得到S1测点对应结构的第3阶固有频率为55.661 Hz，第2阶固有频率为26.627 Hz。从一次滤波后的结果可知，结构的第1阶固有频率存在于15Hz以下。为此，针对结构第1阶固有频率的获取构造了通带截止频率为15 Hz的低通滤波器对信号进行二次滤波处理。滤波信号经HHT处理后的瞬时频率如图10所示。同样对瞬时频率结果进行均值拟合可得S1测点下结构的第1阶固有频率为6.872 Hz。

图10 第二次滤波后第3阶瞬时频率Fig.10 The third instantaneous frequency after the second filtering

对测点S2、S3实测声压信号进行相同的处理，可得结构的前三阶固有频率，如表1所示。从表1中可以看出，利用结构近场辐射声压信号并基于HHT二次滤波时频分析方法可以准确、稳定的获取结构固有频率，前三阶固有频率平均值分别为：55.673、26.672、6.867 Hz，相对于加速度传感器测试数据的最大误差为0.4%。

表1 各测点提取的结构前三阶固有频率Table 1 The first three natural frequencies of the structure extracted from each measuring point

4.3 振型提取

根据表1中两种测量方法识别的钢梁固有频率计算出钢梁的第1阶模态参数如表2所示。表2中将两种测量方法的幅值最大值作为归一化因子，振型拟合点纵坐标的正负应与相位角相同。同种测量方法的其余各点与归一化因子相比即可求出其振型坐标。两种测量方法拟合出的1阶振型如图11所示。由图11可以看出，采用钢梁振动辐射声压信号获取的模态振型与传统方法获取的振型拟合程度较高。从有限的数据结果来看，通过非接触声压测量获取结构的模态参数是较为准确可靠的，该方法为桥梁结构模态参数获取和结构健康监测提供新的手段。