车间通信中基于高斯过程回归的功率分配算法

王 维

(四川师范大学 信息网络服务中心，成都 610066)

1 引 言

5G的高速、低时延特点推助了车间通信(Vehicle-to Vehicle，V2V)的应用[1].除了对数据传输时延以及可靠性具有苛刻的要求外，V2V的安全应用对车辆的状态更新信息的新鲜度具有一定要求.信息年龄(Age of Information，AoI)是评估信息新鲜度的有效指标.依据美国罗格斯大学的Kaul等[2]对信息年龄(Age of Information，AoI)的定义：对于任意系统，任意时刻的AoI表示目的端接收的最新更新信息自产生后所经过的时间[3].

考虑到V2V的安全应用，从AoI角度实现通信的可靠性是十分必要的.事实上，如果AoI能够预先地可靠地估计，就可提前分配传输功率[4]和资源块(Resource Block，RB)，进而保证通信的可靠性.因此，可将AoI超过预定阈值的概率定义为通信的可靠性.

然而，为了准确地估计未来的AoI，需要掌握网络动态知识，即无线信道、车间干扰以及拓扑变化等信息.最近，研究人员开始关注车载网络的AoI的优化问题[5-7].

由于车载网络动态变化，预先获取网络动态信息存在较大的挑战.基于在线集中式策略实时学习网络动态信息和分配资源是一个可行的办法[8].文献[9]采用了模型预测控制(Model Predictive Control，MPC)策略.在确保系统性能优化的同时，掌握动态系统的信息.然而，MPC需预先得到动态系统的准确数据模型，这在车载网络中无法满足.

基于高斯过程回归(Gaussian Process Regression，GPR)是掌握动态系统信息的有效方法.GPR灵活，且对过度拟合[8]具有健壮性.与高斯混合模型(Gaussian Mixture Model，GMM)不同，GPR是非参数化的贝叶斯学习方法，其不受函数形式的约束[10].

为此，提出基于GPR的动态信息的捕获算法GPR-PA.GPR-PA算法主动地学习系统的动态性，估计车辆的未来的AoI，优化所分配的传输功率.仿真结果表明，提出的GPR-PA算法降低了AoI超标概率，降低了平均AoI.

2 系统模型

考虑如图1(a)所示的网络模型.网络内有车、基站、行人和路边单位(Roadside Unit，RSU)组成.由于本文只关注车间通信V2V，车与网络(Vehicle to Network，V2N)、车与RSU(Vehicle-to-RSU，V2R)通信不在本文讨论范围内.

一对车辆的V2V称为通信对模型，如图1(b)所示.假定在一个RSU范围的覆盖范围内有M个通信对.车辆遵照Manhattan移动模型移动.M个通信对共享R个正交的RBs资源，且带宽为W.

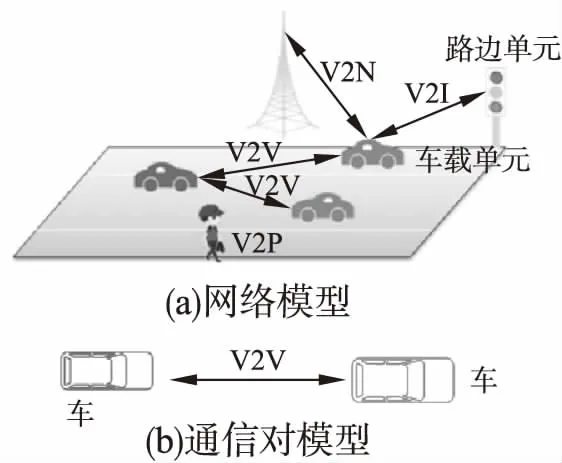
图1 网络模型和通信对模型

将通信时间轴划分为多个时隙，且每个时隙长为τ.用t表示时隙的索引.对于任意一个通信对k，定义一个R维的功率分配矢量：

(1)

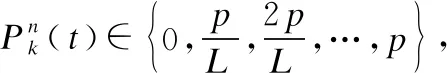
此外，对通信对k所分配的功率上限进行限定，如式(2)所示：

(2)

式中：R表示R个正交的RBs资源集；Pmax为可预支的最大功率.

每个通信对k均有队列缓冲区，用于缓存数据.用Qk(t+1)表述队列的动态变化：

Qk(t+1)=max(Qk(t)-Ik(t)，0)+A

(3)

式中：Qk(t)表示在时隙t通信对k的队列长度；A表示每个时隙的周期的数据包到达率；Ik(t)表示在时隙t通信对k的传输率，单位为每个时隙传输的数据包数.

(4)

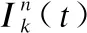
3 GPR-PA算法

GPR-PA算法有两个目标.第1个目标就是提高状态信息更新的可靠性；第2个目标就是掌握动态系统的知识.先将这两个目标进行数学表述，并联立这两个目标建立目标函数，再利用算法1求解，得到最优每个通信对的最优的功率分配值.GPR-PA算法的整个框架如图2所示.

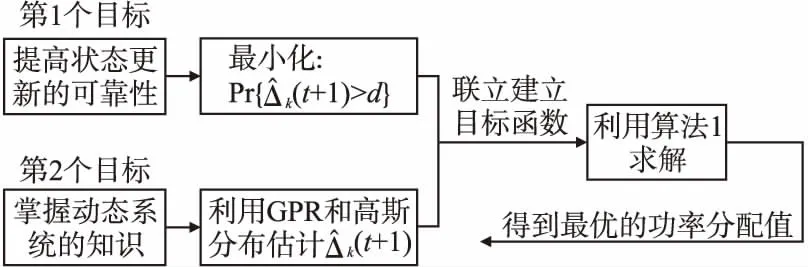
图2 GPR-PA算法框架

3.1 基于GPR的AoI

用AoI评估信息的新鲜度.令Δk(t)表示通信对k在时隙t的开始时刻的AoI，其定义如式(5)所示：

Δk(t)=τt-γk(t)

(5)

式中：γk(t)表示通信对k接收最新信息的时刻.AoI与信道增益、干扰以及所分配的功率相关.因此，利用非线动态系统函数fk(·)估计下一时隙的AoI：

Δk(t+1)=fk(Δk(t)，Pk(t))

(6)

在动态系统中，Δk(t)∈R+表示系统状态.Pk(t)∈p表示在时隙t的控制动作.通过fk：R+×p→R+将控制动作映射到系统状态[8].

利用历史数据估计fk(·)是一个递归问题.采用GPR，对式(6)进行转换.为了简化符号，令yi=fk(xi)，其中xi=[Δk(i)，Pk(i)]表示第i个历史数据输入点；yi=Δk(i+1)表示对应的标量输出.

GPR为非线性回归量，其表述了输入与输出关系.为此，假定fk(·)的先验分布服从高斯过程(Gaussian Processes，GP)[11].注意，此假定并不意味着其完全服从高斯分布，但是给定的协方差函数，GP仍可看作一个最大熵过程(Maximum Entropy Process).

C=[c(xi，xj)]ij，∀xi，xj∈Dk

(7)

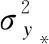
(8)

(9)

式中：c*=[c(x*，x1)…c(x*，xD)]T.y=[y1…yD]T[11].

GPR的计算复杂度随D的增加呈线性快速增长[9].然而，由于车载网络的动态特性，通过丢弃旧的数据使数据库D固定，能够应对计算GPR的复杂度，同时，也不影响GPR性能.

利用协方差函数c(xi，xj)可完备地定义一个GP.为了准确地估计未来的测量有及它们的分布，选择一个协方差函数.为此，引用Matern类协方差函数[12]学习fk(·)：

(10)

式中：Γ(·)表示标准的Gamma函数；B(·)表示二阶的修正的Bessel函数；Matern类协方差函数包括当ν=0.5时的指数自校正函数和当ν→∞时高斯校正函数.

3.2 AoI-感知的功率和RB分配

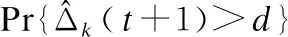
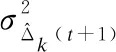
(11)

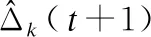
(12)

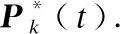
算法1.

输入值：P，αc，αi，D；

初始化：Δk(0)=0，Dk=φ，selectPk(0)∈prandomly

endfor

如算法1所示，第1步，建立输出入值：p、αc、αi和D；第2步，进行初始化：Δk(0)=0，Dk=φ，并从p中随机一个值赋予Pk(0)；第3步，进入循环运算.在每个时隙t，观察Δk(t)，并向数据库里添加所观察的数据，如式(13)所示：

Dk=Dk∪([Δk(t-1)，Pk(t-1)，Δk(t)])

(13)

再判断Dk内的数据量是否超过D.若超过就去除最优的数据，进而保证Dk内的数据量不超过D.

4 性能分析

4.1 仿真环境

考虑250m×250m区域大小的曼哈顿(Manhattan)移动模型[13，14].Manhattan模型由一定多条水平与竖直的街道组成，每条道为双向道，如图3所示.在每个车道的交叉口，移动点可直行、或者左拐、右拐.另外，节点的速度还受到同方节点速度的约束.

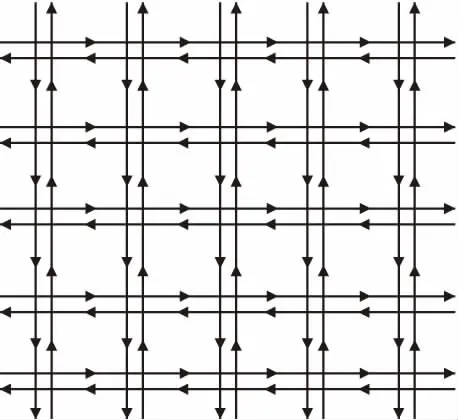
图3 Manhattan模型

仿真参数如表1所示.车辆的平均速度为60 km/h.每个通信对间距离为15m[15].仿真的总时隙为5000 时隙.利用GPML 工具箱求解GPR[16].

表1 仿真参数

在仿真过程中，考虑不同的状态更新到达率为500kbps、1Mbps.并选择两个基准(Baseline)为参照，分析GPR-PA算法的性能.Baseline1：每个通信对随机分配功率，不进行系统动态信息的学习；Baseline 2：每个通信对主动学习动态信息，并基于αi=0求解式(11).

4.2 状态更新到达率的累加分布函数

首先，分析不同的状态更新达到率的辅助累加分布函数(Complementary Cumulative Distribution Function，CCDF)，其反映了AoI超标概率，如图4、图5所示.

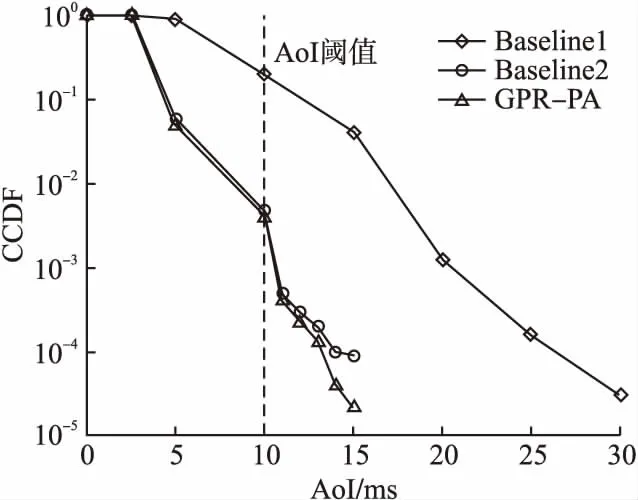
图4 CCDF曲线(状态更新到达率为500kbps)

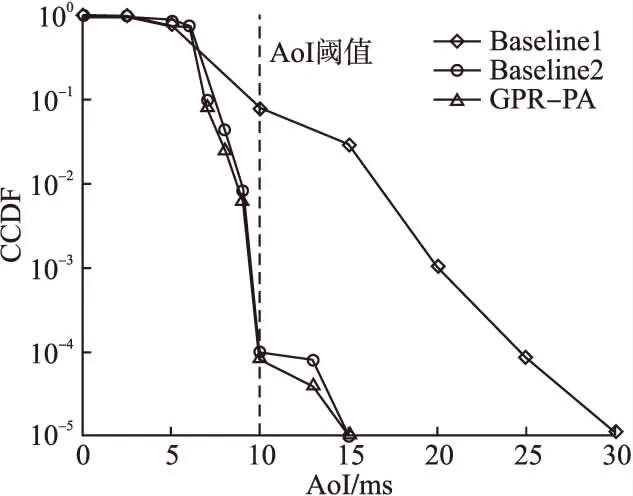
图5 CCDF曲线(状态更新到达率为1Mbps)

图4给出了AoI对CCDF的影响，其中状态更新到达率为500kbps.从图4可知，CCDF随AoI的增加而下降.原因在于：AoI越大，超标概率越低.相比于Baseline1，Baseline2和Proposed的性能得到优化.

图5给出了在状态更新到达率为1Mbps时，CCDF曲线随AoI的变化情况.相比于到达率500kbps时，到达率为1Mbps时的AoI的超标概率随AoI增加而下降的速度更快.在AoI=10ms时，GPR-PA算法的CCDF已降至0.0001.

4.3 根均方误差及超标概率

本小节分析不同数据库容量D对下一个时隙的AoI估计的性能，并选用根均方误差(Root Mean Square Error，RMSE)作为性能指标：

(14)

图6给出不同数据库容量D对估计性能和超标概率的性能影响，其中R=20，αc=1.从图6(a)可知，当D≤200时，GPR-PA算法估计的根均方误差RMSE随数据库容量D的增加而下降，并且下降速度较大.当D>200后，RMSE随D的增加呈缓慢增长，估计的误差开始增加.这说明，并非数据库容量D越大，估计精度越高.原因在于：车载网络动态变化，历史观察数据的不确定.

图6 数据库容量D对估计性能和超标概率的影响

图6(b)给出概率Pr{Δ(t)>d}随数据库容量D的变化情况.该曲线趋势与图6(a)相类似.在D≤200时，概率Pr{Δ(t)>d}随D的增加而快速下降.在D>200后，概率Pr{Δ(t)>d}随D的增加反而上升，但上升速度变慢.

4.4 αi对平均AoI和超标概率的影响

图7(a)给出GPR-PA和Baseline2的超标概率Pr{Δ(t)>d}随αi的变化情况.其中Baseline2表示每个通信对主动学习，但αi=0.结合式(11)可知，αi=0意味在功率分配时，不考虑AoI方差.

从图7(a)可知，当权重系数αi达到100后，AoI的超标概率下降.而αi达到100后，超标概率上升，性能下降.原因在于：αi值越大，每个通信对就更倾向选择控制动作，学习更多的系统知识，而不是降低AoI的超标概率.并且当αi大于200后，GPR-PA算法的超标概率大于Baseline2的超标概率.这表明，并非数据库容量D越大，性能越优，需合理地选择数据库容量D.

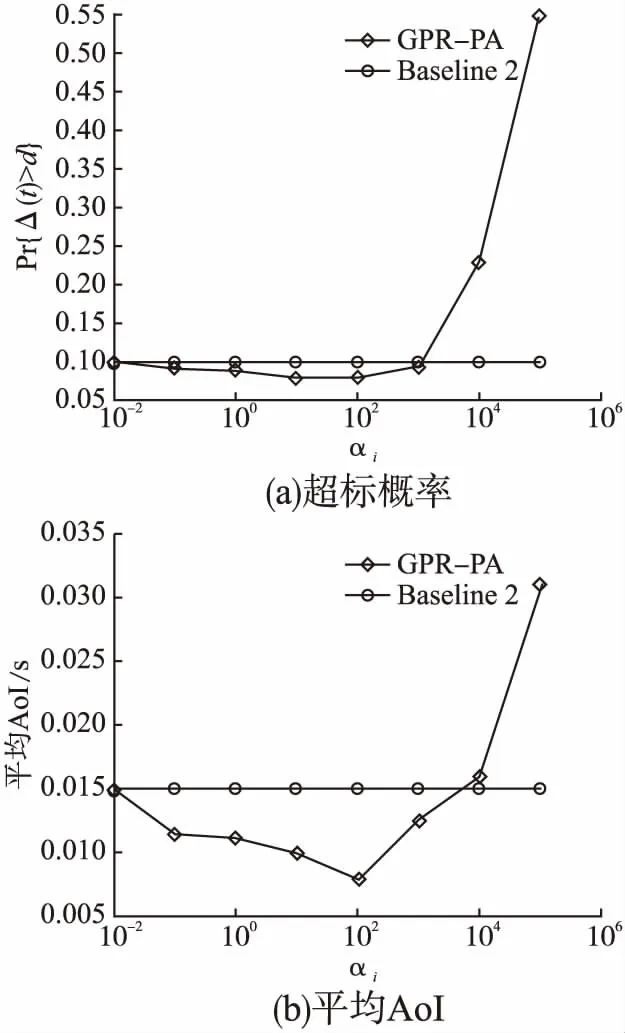
图7 αi对平均AoI和超标概率的影响

图7(b)给出了平均AoI随αi变化曲线，其与图7(a)曲线类似.在αi小于100时，αi的增加，能够降低平均AoI，提高了信息的保鲜度，并且优于Baseline2环境下的性能.当αi大于100后，平均AoI不再随αi的增加而下降，反而上升.

5 总 结

本文针对动态的车载网络，对传输功率和RB的分配进行了研究，其主要目的就是在下一时隙AoI超过阈值的概率与最大化学习动态系统知识间达到平衡.GPR-PA算法通过GPA主动学习网络的动态信息，并估计下一时隙的AoI.仿真结果表明，相比于其他基准算法，提出的GPR-PA算法降低了AoI超过阈值的概率.