基于SPSS的西藏饮用天然水电导率与溶解性总固体相关性分析*
2021-11-20邵蓓王祝周会东刘坤阳胡亚燕杜建军
邵蓓 王祝 周会东 刘坤阳 胡亚燕 杜建军
(西藏自治区地质矿产勘查开发局中心实验室,西藏 拉萨 850033)
0 引言
电导率是用数字来表示水溶液传导电流的能力,溶解性总固体(TDS)是水中溶解的无机矿物成分的总量,它们的大小都是由水溶液中离子的组成和离子的含量决定的,因此它们之间存在着相关关系,而且相关关系显著[1-3]。因此,在水质的分析检测中利用这种关系所具有的规律性对检测数据进行合理性分析,可确保水质检测数据的准确可靠[4]。此外,在水质监测中,采用由电导率推算溶解性总固体的方法,比较简便、准确,可适用于现场水质监测[5]。
对于某一区域来说,由于离子组成相对稳定,因此电导率与溶解性总固体的关系也相对稳定[6]。张启新等[7]以甘肃省河西走廊张掖盆地为例,采用最小二乘法对矿化度、电导率进行一元线性回归,结果显示重碳酸盐型水矿化度/电导率≈0.57,硫酸盐型水矿化度/电导率≈0.69。丁迎红[8]计算得到长江水溶解性总固体与电导率的比值平均值为0.721,龙源水的平均比值为1.09。齐齐哈尔市地区地下水溶解性总固体与电导率之间的数量关系,系数0.55~0.7 随不同水质而异[9]。周贝等[10]分析了崂山矿泉水的源水,其电导率与溶解性总固体线性关系较为显著,其比值为0.84。
SPSS(Statistical Product and Service Solutions)是世界上应用最早的统计分析软件,目前广泛应用于自然科学、技术科学、社会科学的各个领域。利用IBM SPSS Statistics 22.0对西藏518件饮用天然水的分析数据进行相关性和回归分析,结果显示,西藏饮用天然水溶解性总固体与电导率具有极高的正相关性,二者线性关系显著,其比值近似为0.863。
1 材料与方法
1.1 试验材料
试验用水样为西藏饮用天然水样品,包括了西藏7 个地区的地表水和地下水样品518 件,水样的采样和测试时间为2019 年8 月至2021 年6 月,具有充分的代表性。
1.2 测定方法
电导率:电导率的测定采用电极法。
溶解性总固体:溶解性总固体的测定采用105℃烘干法,依据GB 8538-2016《饮用天然矿泉水检验方法》,由于水样经烘干后得到的蒸发残渣与离子总量相比较,水中HCO3-损失了近一半(50.8%)[7],因此将蒸发残渣含量加上碳酸氢盐含量的一半即为溶解性总固体。
1.3 数据分析统计
本文对518件水样的电导率和溶解性总固体数据进行统计分析,数据的汇总采用Excel完成,数据的相关性分析、回归分析和图件制作采用IBM SPSS Sta‐tistics 22.0统计软件完成。
2 结果与分析
2.1 水化学指标超标数据的剔除
在数据统计中发现,参与统计的518件水样,部分地下水样实际为地下热水,由于在地下热源的作用下水温通常较高,在高温高压环境下水与岩体充分反应、溶滤,水中矿物元素包括一些重金属元素等含量通常较高,不适合作为饮用水。此外,依据GB 5749-2006《生活饮用水卫生标准》、GB 8537-2018《食品安全国家标准饮用天然矿泉水》,对溶解性总固体、Na、氯化物、B、硫酸根、总硬度、氟化物、pH、硝酸盐等饮用水主要限值指标进行统计。统计结果显示:518 件水样中,地热水41 件,TDS 超标53 件(TDS >1000 mg/L),Na 超标46 件(Na >200 mg/L)、氯化物超标25 件(Cl->250 mg/L)、硼超标21 件(B >5 mg/L)、硫酸盐超标16 件(SO42->250 mg/L)、总硬度超标25件(总硬度>450 mg/L)、氟化物超标58 件(F->1.5 mg/L)、pH 超标61 件(其中pH >8.5 53 件,pH <6.5 8 件)、硝酸盐超标4 件(NO3->45mg/L),剔除掉地热水及水化学指标超过饮用水标准限值的数据组(其他限值及毒理学指标如重金属元素等由于在水样中含量轻微,可忽略不计,本文未做统计),最终得到符合饮用水标准的水样382件。
2.2 离群值的剔除
由于测量误差等因素的存在,电导率、溶解性总固体可能存在异常值,最终影响溶解性总固体与电导率的比值。利用SPSS 22.0 统计分析软件的“探索性分析”功能对数据进行过滤和检查,识别离群值和极端值。以“溶解性总固体与电导率的比值”为变量,通过绘制箱图来描述个案之间差异的特征,见图1。

图1 溶解性总固体与电导率的比值箱图
图1所示的是以“溶解性总固体与电导率的比值”绘制的箱图,箱子的上边线表示第75 百分位数,下边线表示第25 百分位数,中间的的线表示中位数,箱子上下的两条细横线表示的是除离群值和极值的最大值和最小值。离群值是指离箱子的上下边线的距离为箱子高度的1.5 倍至3 倍的变量值,本图中用“O”表示。极值是指离箱子的上下边线的距离为箱子高度的3倍以上的变量值,本图中用“*”表示。离群值和极值旁的数据为数据组的编号。
根据图1 所示,经统计分析有离群值13 组(包含极值1 组),将其剔除,最终获得符合统计分析要求的西藏饮用天然水数据为369组。
2.3 电导率与溶解性总固体的相关性
相关分析是研究事物之间是否具有相关性及相关性强弱的一种统计方法[11]。利用SPSS 22.0 数据统计软件,对369 组西藏饮用天然水电导率与溶解性总固体的相关性进行分析,其分析数据如下:
表1 是相关性分析的描述性统计资料,参与统计分析的电导率、溶解性总固体个案(N)均为369个,电导率平均值为326.5 μS/cm,溶解性总固体平均值为269.9 mg/L。表2 是电导率与溶解性总固体的相关性分析结果,从结果中可以看到,电导率与溶解性总固体之间的皮尔逊相关系数为0.983,显著性概率值P=0.000 <0.01,表示在0.01 的显著性水平上(99.0%的置信度)极显著。在统计分析中,常利用相关系数定量地描述两个变量之间线性关系的紧密程度。相关系数是描述线性关系强弱和方向的统计量,取值范围为-1~1。如果因变量值随着自变量值的增大而增大,或者随着自变量值的减小而减小,我们称之为正相关,相关系数大于0。但是如果因变量值随着自变量值的增大而减小,或者随着自变量的值减少而增大,我们称之为负相关,相关系数小于0[11]。一般认为:皮尔逊相关系数(r)的绝对值越大,相关性越强:在0.8~1.0之间是极强相关;0.6~0.8 之间是强相关;0.4~0.6 之间是中等强度相关;0.2~0.4 之间是弱相关;小于0.2 可以认为两变量是极弱相关或无相关。西藏饮用天然水电导率与溶解性总固体的皮尔逊相关系数为0.983,说明二者之间具有极强的正相关性,即当电导率增加时,溶解性总固体也会相应增加。由于在相关性分析中,电导率与溶解性总固体互为自变量和因变量,当溶解性总固体增大时,电导率也会相应增加。

表1 描述性统计资料
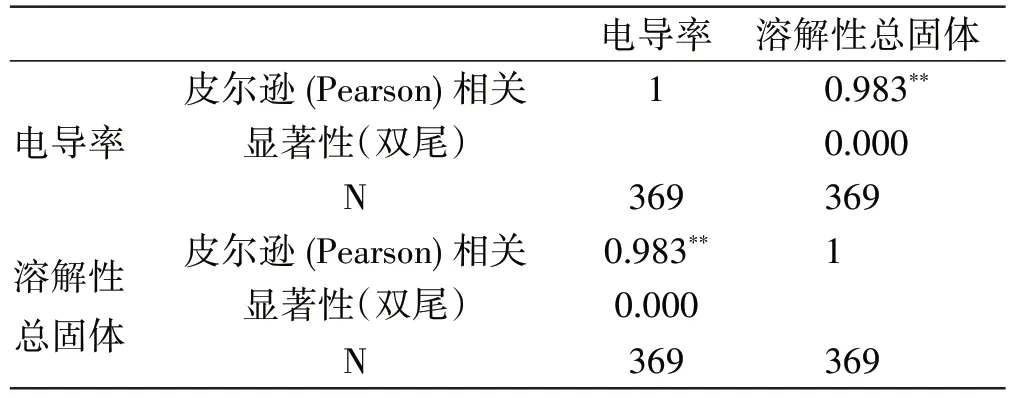
表2 相关性分析结果
2.4 电导率与溶解性总固体回归分析
相关分析只表明变量是否相关、相关方向和密切程度,不能指出变量间相互关系的具体形式,回归分析指的是确定两种或两种以上变量间相互依赖的定量关系的统计分析方法[11]。
如果自变量和因变量之间呈线性关系时,这时进行的回归分析就是线性回归。利用SPSS 22.0 统计软件,以电导率为横坐标、溶解性总固体为纵坐标作散点图(见图2),来判断二者是否具有线性关系。
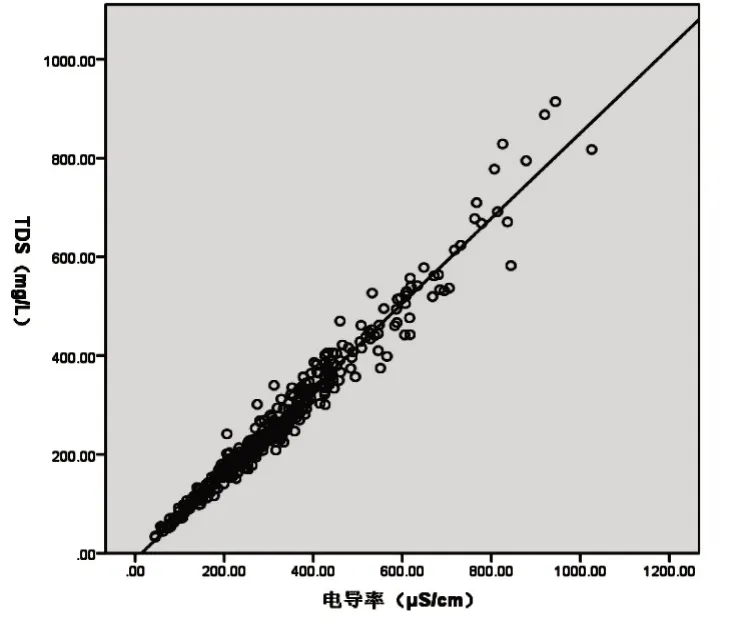
图2 电导率与溶解性总固体关系散点图
由图2可知,样本点的分布仅仅围绕在一条直线上下,且随着电导率的增加溶解性总固体也相应增加,表明电导率与溶解性总固体之间存在线性正相关关系。
以电导率为自变量、溶解性总固体为因变量,利用SPSS 22.0 数据统计软件来对电导率与溶解性总固体进行线性回归分析,回归分析结果如下:
回归分析以电导率为自变量、溶解性总固体为因变量建立模型方程,模型方程中,x 代表自变量电导率,y代表因变量溶解性总固体,通过一元线性方程来描述x 和y 的关系,可以根据自变量x 预测因变量y。表3为模型摘要,R 平方值为决定系数,用于判定模型方程的拟合优度,R 平方值0.983 意味着自变量x(电导率)可以解释因变量y(溶解性总固体)98.3%的变化,模型拟合效果良好。表4 是回归方程的F 检验结果,显著性值P=0.000 <0.01,说明线性回归方程显著。表5 是对回归系数的T 检验结果,显著性概率Sig=0.000 <0.01,表明回归系数B 有统计学意义,电导率与溶解性总固体之间是正比关系,而且极显著。因此,建立西藏饮用天然水电导率与溶解性总固体的回归方程为:溶解性总固体=电导率×0.863-11.772,溶解性总固体与电导率的比值近似为0.863。

表3 模型摘要a
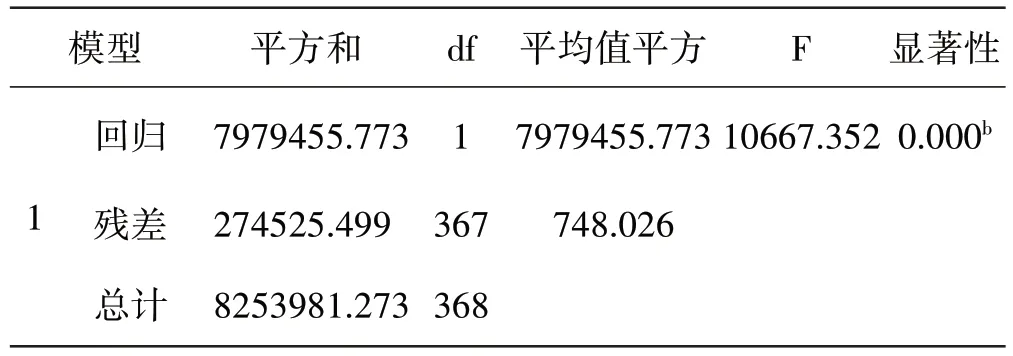
表4 ANOVAa

表5 系数a
3 结论
利用SPSS 统计分析软件对西藏饮用天然水电导率与溶解性总固体进行相关性分析的结果表明,电导率与溶解性总固体的皮尔逊相关系数为0.983,说明电导率与溶解性总固体之间具有极强的正相关性,即当电导率增加时,溶解性总固体也会相应增加,而当溶解性总固体增加时,电导率也会相应增加。
利用SPSS 统计分析软件对西藏饮用天然水电导率与溶解性总固体进行回归分析的结果表明,二者线性关系显著,关系为:溶解性总固体=电导率×0.863–11.772,拟合决定系数R2=0.983,溶解性总固体与电导率之间的比值系数近似为0.863。
