基于两步折减法的含天然气水合物沉积物海底斜坡稳定性分析

2021-11-20赵亚鹏刘乐乐袁庆盟刘佳棋

天然气工业 2021年10期

赵亚鹏孔亮刘乐乐袁庆盟刘佳棋

1. 青岛理工大学理学院 2. 青岛理工大学土木工程学院3. 自然资源部天然气水合物重点实验室•中国地质调查局青岛海洋地质研究所4.青岛海洋科学与技术国家实验室海洋矿产资源评价与探测技术功能实验室

0 引言

作为一种能量密度高、环境污染小、分布广泛的新型能源，天然气水合物（以下简称水合物）受到世界各国的密切关注[1]。当水合物储层的温压环境发生变化时，水合物就会发生分解，其胶结作用消失并产生超静孔隙水压力，水合物及其周围地层强度降低，进而引发各种地质灾害[2-5]。同时这些地质灾害往往以“灾害链”的形式存在[6]，伴随灾害范围的不断扩大，最终诱发长期的、大规模的地质灾害[7]，而以水合物分解为主导因素的海底滑坡就是其中的典型代表。

对于普通的陆地边坡，目前已经进行了较为深入的研究。针对边坡稳定性问题，广泛采用极限平衡法和数值分析法[8-9]进行分析，同时基于不同考虑角度，衍生出一系列的细化研究方法，如极限平衡法中的简化Bishop法[10]、Janbu法[11]、基于塑性力学的上限分析法[12]等。数值分析方法中，则以强度折减法为代表，得到了广泛的应用[13-14]。与陆地边坡相比，海底斜坡具有更为复杂的地质环境，但是两者仍具有诸多共性，可以采用类似的研究方法进行分析，如年廷凯等[15-16]基于极限分析上限方法对海底斜坡进行稳定性分析；Song等[17-18]以水合物分解影响为出发点，采用强度折减法对不同考虑因素下的海底斜坡稳定性进行了研究；Kong等[19]基于强度折减法对海底斜坡进行了多因素敏感性分析；修宗祥等[20]以南海海底斜坡为研究对象，分别采用极限平衡法和强度折减法进行了对比研究，发现两种方法结果一致。

整体而言，目前对于水合物分解影响下的海底斜坡稳定性问题，较多的研究者采用了强度折减法，其存在着以下不足：①以强度折减法所得安全系数进行稳定性分析，缺乏对于初始地应力平衡基础上的水合物分解影响效果研究；②多数研究规避了初始地应力平衡的问题，而初始地应力平衡显然与水合物分解之间有着直接的关系，因此如何实现初始地应力平衡、水合物分解、强度折减三者的有效统一，就成为问题的关键；③对于复杂环境下海底斜坡的多因素影响研究不足，专门针对含水合物沉积物海底斜坡的多因素分析较为鲜见，尤其是斜坡倾角与安全系数之间的关系有待于进一步研究。为了解决上述问题，笔者提出将初始地应力平衡、水合物分解、强度折减统一考虑的“两步折减法”，并利用该方法对含水合物沉积物的海底斜坡稳定性进行了综合研究。

1 两步折减法

1.1 强度折减法

强度折减法最早由Zienkiewicz等[21]提出，作为一种边坡稳定性评价方法，其原理简单、物理意义明确、评价指标直观，因而被许多学者广泛采用。折减后的抗剪强度参数可表示为：

式中cm和φm表示维持平衡所需要的或土体实际发挥的抗剪强度，单位分别为kPa和（°）；c和φ表示土体所能够提供的抗剪强度，单位分别为kPa和（）；Fr表示强度折减系数，无量纲。

在有限元分析中，首先假定不同的Fr，根据折减之后的强度参数进行计算分析，在计算过程中不断增加Fr的值，直至达到临界破坏，而破坏时对应的Fr就是边坡稳定的安全系数。

1.2 两步折减法

在进行强度折减时，一般需要先进行初始地应力的平衡，在此基础上再进行强度折减。对于绝大多数的研究对象，如边坡，其在长期的地质作用下已经达到一种稳定状态，可以认为边坡的力学参数保持不变，当对其进行强度折时，只需对其进行初始地应力的平衡，再进行强度折减即可。而对于一些近期经受过扰动影响（如地震、爆破等）的地质对象，由于扰动作用，其力学参数发生了一定的变化。因此，有如下考虑：①由于时间上的不足，其远未达到重新的地应力平衡，如果将新的力学参数赋予地质对象，再进行初始地应力的平衡和强度折减显然与实际情况不符；②根据研究目的的不同，所需研究内容可能就是初始地应力平衡基础之上的扰动影响分析；③对于扰动地质对象所发生的力学参数变化，可能是整体性的，也可能是局部岩层的。

基于以上分析并结合ABAQUS强度折减实现方式，提出两步折减法（经过前期工作，初始地应力平衡采用“自动地应力平衡法”），将上述考虑因素进行“归一化”处理。主要步骤如下：

1）增加场变量，将需要进行初始平衡时的各岩层力学参数设置为对应场变量初值（需小于1）。

2）根据实际情况，将受扰动影响后的力学参数赋予地质对象整体或部分岩层，并设置为对应场变量值“1”。

3）在场变量值“1”对应力学参数基础上进行参数折减，赋予各场变量值对应力学参数。

4）建立第一个分析步（初始平衡），并采用场变量初值对应的力学参数。

5）建立第二个分析步，并进行强度折减，折减至场变量值“1”。

6）建立第三个分析步，并进行强度折减，折减至场变量终值。

当需要对不同扰动程度的影响效果进行分析，或者对不同扰动程度地质对象进行强度折减时，只需对扰动岩层场变量值“1”对应力学参数进行修改即可。两步折减法可用表示为：

式中c1和φ1表示受扰动土体所能够提供的抗剪强度，单位分别为kPa和（）；c和φ表示未受扰动土体所能够提供的抗剪强度，单位分别为kPa和（）；F(c)和F(φ)表示函数关系式，代表未受扰动与受扰动土体抗剪强度之间的关系，由实际情况或研究需要确定。

综上所述，两步折减法所解决的问题可概述为“变动强度稳定性分析”（如地震、爆破、水合物分解、堆载预压等），尤其适用于部分区域强度变化的整体稳定性对比分析。其主要优势在于：①避免了重复进行地应力平衡以及力学参数赋值；②可实现不同扰动程度、不同扰动形式（线性、非线性）边坡稳定性分析；③可实现小范围强度变化的整体稳定性分析；④通过包含多个分析步的单一“cae”文件实现初始地应力平衡（第一个分析步）、扰动影响（第二个分析步）以及强度折减（第三个分析步）的综合分析。

1.3 边坡失稳判据

根据现有经验，边坡失稳判据一般有3种，分别为塑性区贯通、位移突变以及计算不收敛[22-23]。在强度折减过程中，3种判断方法呈现时间上的递进关系，首先是边坡底部塑性区形成并向上发展，最终塑性区贯通，接着边坡顶点发生位移突变。随强度进一步折减，塑性区不断扩大，位移增加，导致边坡大范围失稳，进而引起计算不收敛。虽然3种判据所得安全系数存在差异，但是由塑性区贯通至计算不收敛，折减系数变化在5%以内[24]。实际计算时只要采用统一标准，所得安全系数即可作为定性或定量标准。考虑到前两种方法需要结合云图人为判定，笔者采取计算不收敛作为边坡失稳判定的统一标准。

2 工程案例及模型建立

2.1 工程案例及适用性分析

工程案例以含水合物沉积物的海底斜坡为研究对象，探究在海水压力作用下，水合物分解对海底斜坡稳定性的影响。根据地质情况[25-26]并结合相关研究成果[17,19]，在不考虑地震、海平面变化、人为扰动等非常规因素影响时，可认为其主要受斜坡角度、海水深度、水合物分解程度、水合物埋深与水合物厚度等因素影响。

水合物分解会引起水合物储层力学参数的降低，因此，需要考虑的关键问题在于当水合物分解程度不同时，与之对应的水合物储层力学特性的变化；采用强度折减法对水合物分解后的边坡进行分析时，不同分解程度所对应的基数“1”（宏观海底斜坡整体力学参数）也不相同；此外，不同分解程度水合物储层在分解之前的状态是完全相同的（均是在上覆海水压力以及自重应力下的平衡状态），因而不能简单地将水合物分解后的力学参数赋予储层后再进行初始平衡和强度折减。通过以上分析，采用“两步折减法”可以简单而有效地解决上述含水合物沉积物海底斜坡问题。

2.2 模型建立

本文所建含水合物沉积物海底斜坡模型为二维平面模型（图1），根据地震反射剖面图以及似海底反射层（Bottom Simulating Reflector，缩写为 BSR）位置（图2），可确定水合物储层埋深、厚度等实际尺寸。依据本文参考文献[19,23]并考虑优化，模型坡长1 800 m、坡角6°，模拟水深800 m，水合物储层厚度30 m、埋深250 m，坡顶、坡底长800 m，模型总跨度3 390 m。将模型划分为上覆岩层、水合物层、周围岩层、下伏岩层共4层岩体，采用三角形平面应变单元类型，并对水合物层进行加密。本构模型采用摩尔—库仑模型，边界条件为：模型左右边界限制水平位移，模型底部边界限制各个方向位移。考虑到气、固、液三相耦合的非确定性，同时强度折减主要与c、φ相关，因此本文假设水合物分解过程中水、气可快速排出，不考虑孔隙压力的影响，即模拟砂质水合物储层的分解过程。根据水合物力学特性实验以及相关模拟研究成果[19,27-30]，经试算模拟后，本文力学参数如表1所示，水合物饱和度为25%。

图1 海底斜坡示意图

图2 地震反射剖面图（框选区域深色为BSR）

表1 海底斜坡力学参数表

3 水合物分解影响

考虑到引起水合物分解的原因众多，而地震、火山喷发、气候变化、海平面下降等[6]都会引起温压环境的显著变化，进而造成水合物的大范围分解，同时考虑到模型尺寸以及对“两步折减法”的有效验证，本文水合物分解为储层整体分解。图3、4为统一图例范围后不同水合物分解程度下的垂直应力、位移云图，对图中峰值数据进行汇总，得到表2。由图3、4及表2可知，水合物分解主要对位移云图产生影响，对于应力云图的影响则较小，不同分解程度下的应力云图基本一致；水合物分解后，储层上方产生了显著的位移变化，由坡脚至坡顶位移逐渐增大，最大值出现在水合物上覆岩层坡顶区域。随分解程度的增加，峰值区域逐渐由坡顶向坡脚扩散。

表2 水合物不同分解程度的应力、位移峰值表

图3 水合物不同分解程度应力云图

图4 水合物不同分解程度位移云图

由于应力峰值出现在模型底部，而水合物影响范围有限，整体云图中并不能体现出水合物分解对应力场所造成的影响。因此有必要对水合物区域的应力变化进行分析，同时考虑深度方向上的应力、位移变化，布设S1～S4共4条测线，S1沿水合物层方向，S2～S4则基本沿垂直方向（图5）。

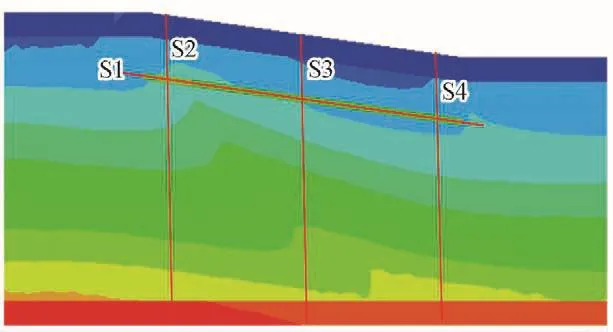
图5 测线布设图

3.1 横向分析

图6为S1测线应力、位移变化曲线，横坐标蓝色加粗为水合物储层区域，坐标200～2 000 m。由图6-a可知，不同分解程度位移曲线呈现相似的变化规律，均是坡顶位移大于坡脚位移，最大位移出现在图示坐标500 m处，与位移云图一致，即最大位移出现在距坡顶一定距离处；随水合物分解程度的增加，测线整体位移不断增大，峰值逐渐升高；值得注意的是水合物储层下边界处位移由初期的升高变为陡降，且陡降幅度随分解程度的升高而增大。这是因为当水合物分解后，应力释放，下边界处受到周围岩层的“挤压”作用（类似于采矿中的“底鼓”与“片帮”[31-32]）并产生“挤压位移”，其与分解造成的“分解位移”相互影响，分解初期水合物储层下边界的“分解位移”相对“挤压位移”要小，因此呈现升高的形态；随着分解程度的增大，“分解位移”不断增大，同时结合图6-b，水平方向“挤压位移”与“分解位移”方向相反，因此两者叠加的总位移相较于“分解位移”要小得多，即呈现出陡降的形态。

由图6-b可知，水平位移整体规律与图6-a类似，不同的是在水合物储层两端位移为负值，测线整体则为正值。这表明，在水合物分解过程中水合物储层水平位移沿储层倾向正方向，两端则沿倾向负方向，这是水合物分解后周围岩层的“挤压应力”与斜坡坡面水压共同作用的结果。由于斜坡的倾斜作用，坡面水压对岩层具有沿倾向负方向的推力作用，水合物储层下边界在“挤压应力”与坡面水压共同作用下产生了沿倾向负方向的水平位移；根据相关文献[33-34]，斜坡附加应力存在非对称性，越靠近斜面坡顶附加应力越小，即水合物储层上边界的“挤压应力”远小于下边界，因此上边界沿倾向正方向的“挤压应力”被坡面水压所影响，最终产生沿倾向负方向的水平位移；随水合物分解程度的升高，两端位移逐渐减小，由倾向负方向向正方向转变，这表明水合物分解所引起的位移效果在不断向两端扩展。

图6 S1测线应力、位移变化曲线图

根据图6-c，竖向位移变化规律与图6-a、b一致，随分解程度的增加，竖向位移不断增大，整体呈现负值，即产生了向下的竖向位移。同样在坡脚储层下边界处位移受水合物分解的影响较小，坡脚处位移的降低相对于6-a、b则要“平缓”，表明坡脚处位移的陡降主要由水平位移陡降所引起。

图6-d为应力变化规律图。在水合物层上下边界之外，应力基本不受水合物分解的影响，而在水合物层，随水合物分解程度的增加，应力不断降低，这与位移变化规律相反。当水合物分解程度相对较低时，应力曲线呈现坡顶高，坡脚低的趋势，峰值同样出现在图示坐标500 m处，这与位移曲线一致，而随水合物分解程度的增加，应力曲线逐渐趋于平缓，即水合物层区域应力基本保持一致。

由以上分析可知，水合物分解所引起的位移、应力变化主要对水合物储层区域产生影响，尤其是靠近坡顶处最为明显。考虑到目前水合物试采主要以直井为主[35]，因此对于实际海底斜坡区域的天然气水合物开采，其直井位置应尽量避免设置在坡顶附近，而应设置于坡脚或远离斜坡区域。

为了更加直观地了解水合物分解所造成的影响，取S1测线代表区段（300～2 000 m），对其进行上段（300～1 000 m）、下段（1 000～2 000 m）的划分，分别求得不同分解程度下代表区段、上段、下段的位移与应力均值，如图7-a所示；根据应力变化曲线图6-d，同样取上段（200～600 m）、下段（800～1 200 m）两个代表区段，分别求取不同分解程度下的应力均值，并作差，得图7-b。

由图7-a可知，无论是上段位移还是下段位移，均与水合物分解程度呈正相关的关系，且随分解程度的增加，其位移增长幅度也逐渐升高，相同分解程度下，上段位移大于下段位移，这与位移云图所对应；应力则随水合物分解程度的增加呈负相关的关系，即水合物分解程度越高，应力越小。

由图7-b可知，当水合物分解程度较低时，上、下段的应力差值较大，而随水合物分解程度的增加，上、下段的应力差值逐渐变小，直到水合物完全分解，上、下段应力几乎相等，即水合物分解对于“斜坡应力”分布具有“稀释均化”的影响效果。

图7 代表区段位移、应力变化曲线图

3.2 纵向分析

图8为水合物不同分解程度下的S2～S4测线位移变化曲线。根据图8-a，纵向方向上，位移变化主要集中在水合物储层及其上部区域，而水合物储层以下位移变化甚微；随水合物分解程度的增加，位移整体不断升高，随坐标自上而下，位移单调递减，且水合物分解程度越大，递减趋势越明显。

由图8-b，S2～S4呈现不同的变化规律，在水合物层及以上区域，随坐标自上而下，S2测线单调递减，S3及S4则单调递增，且越靠近坡脚，递增趋势越明显，同一坐标值下，S2位移最大，S3次之，S4最小；在水合物层以下区域，各测线单调递减，在同一坐标值下，S3位移最大，S2次之，S4最小，这一大小规律与水合物上部区域截然不同。

图8 S2～S4测线位移变化曲线图

结合位移云图，分析原因如下：由于斜坡的倾斜特性，水合物分解后，位移首先从坡顶位置开始逐渐向坡脚呈现“楔形”状扩散（图4），S2测线位于坡顶位置，当水合物分解50%时，S2测线水合物上部区域处于位移“完全发育”范围内（云图深红色区域）；而S3及S4由于远离坡顶，并未处于“完全发育”范围内，仅是靠近水合物层部分处于“楔尖”位置，因此该处位移大于其上部位移。S4处于坡脚位置，测线顶部位移变化相对较小，其与“楔尖”区域位移差值更大，递增趋势也更为明显。将图4中图例范围进一步离散发现，水合物层上部位移显著增加的同时，下部区域位移呈现下凹“圆弧形”分布，因此由于位置差异性，测线S3位移最大，S2及S4位移较小。基于S2～S4测线的位移大小关系，并注意到位移云图的“圆弧形”分布与最终形成滑坡的“圆弧形”坡面极为相似，可知，含水合物沉积物海底滑坡的形成与水合物分解所引起的位移变化具有直接关系。

3.3 影响实质

通过横、纵向的综合分析可知，水合物分解的影响范围有限，主要对纵向上部区域、横向储层范围区域产生影响。同时可以得出如下结论：水合物分解是一个应力释放、位移增加的动态过程，而位移增加的大小则与应力释放程度相关。由于海底斜坡的倾斜特性，地应力平衡后沿斜坡层面的应力分布存在不均匀性，这种不均匀性呈现坡顶大坡脚小的趋势。水合物分解过程中，岩层应力得以释放，其随斜坡分布的不均匀性消失，位移则重新呈现不均匀特性，即由坡顶至坡脚，位移逐渐减小，这与所释放的应力相对应。因此水合物分解的影响实质是将沿斜坡分布的“应力非均匀性”转换为“位移非均匀性”，且位移大小与分解前后应力差值成正相关关系。

从动量的角度分析，取水合物储层一微元，在水合物分解过程中，满足式（3）：

式中F表示水合物分解过程中微元所受平均合外力，N；Δt表示水合物分解时间，s；dm表示微元质量，kg；Δv表示水合物分解过程中微元平均速度变化量，m/s。

由图4可知，水合物分解过程伴随着位移的增大，即合外力发生了变化，而各微元质量dm近乎相等（排出的水、气相对储层质量较小），时间Δt相同，Δv由F所决定。根据图6-d，水合物分解之前，沿斜坡层面应力呈现坡顶大坡脚小，而在水合物分解结束后，沿斜坡方向应力几乎相等，因此这一过程中，沿坡脚至坡顶微元所受合外力F逐渐增大，即Δv沿坡脚至坡顶逐渐增大，则相同时间内，越靠近坡顶则位移越大。

同时根据上述分析，当对稳定性较差的海底斜坡区域进行天然气水合物开采，或由于水合物开采可能引起海底滑坡时，可考虑采取“直井＋水平井”并结合多分支孔的联合开采方式（图9），在水合物储层下部区域设置水平井，并将直井设置于远离斜坡区域，而这种非单一直井的多井联合作业模式也是未来水合物开采的发展趋势[36]。

图9 多井联合作业模式图

4 海底斜坡稳定性影响因素的正交试验

利用SPSS软件构建了考虑斜坡倾角、水深、水合物分解程度、水合物层厚度，水合物层埋深的5因素5水平正交模拟试验方案，以探究不同因素对于海底斜坡稳定性的影响，试验方案如表3所示。

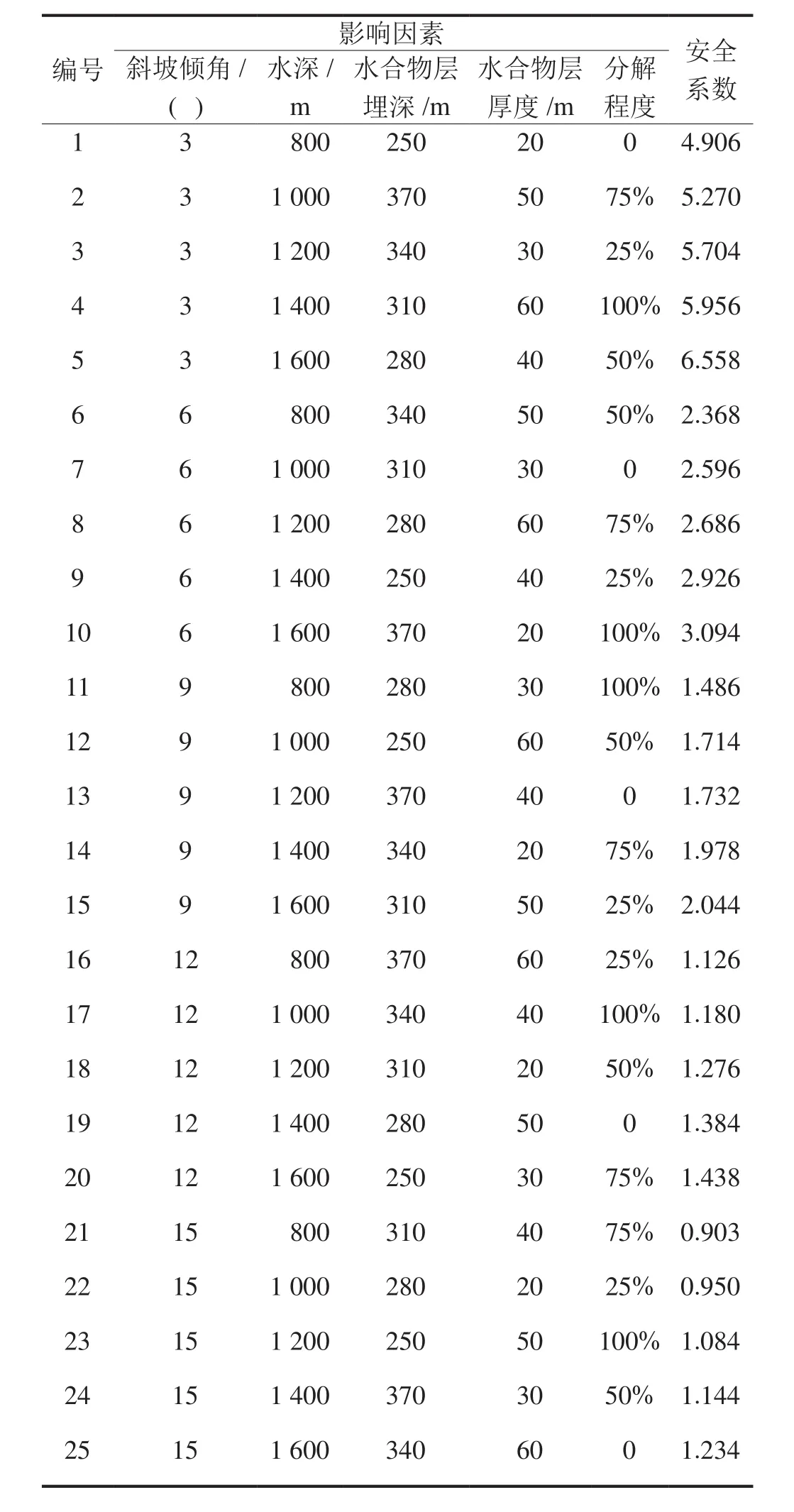
表3 正交试验设计表

4.1 极差分析

极差分析可以直观且简单的确定不同因素对于试验结果影响的主次关系。各因素水平的极差分析结果，如表4所示，其中Ⅰ～Ⅴ表示各因素的不同水平值，均由小至大排列，R表示极差。根据表4可知，RA（斜坡倾角）＞RB（水深）＞RE（分解程度）＞RD（水合物层厚度）＞RC（水合物层埋深）。即各因素对试验结果影响程度由强到弱依次为A（斜坡倾角）＞B（水深）＞E（分解程度）＞D（水合物层厚度）＞C（水合物层埋深）。同时还可发现RA、RB远大于 RC、RD、RE，而 RC、RD、RE之间差别并不明显。

表4 极差分析表

4.2 方差分析

极差分析虽然可以直观地确定影响因素间的主次关系，但是不能有效区分试验结果之间的差异来源，即无法判断试验结果差异是否是由于因素不同而引起的，而方差分析则可以弥补极差的不足，实现各因素对试验结果影响的显著性分析。方差分析结果如表5所示。根据表5，斜坡倾角、水深的显著性水平分别为0和0.047，均小于0.05，表明这两个因素对于海底斜坡安全系数具有显著影响，尤其是斜坡倾角对于海底斜坡的安全系数具有极其显著的影响；储层埋深、水合物层厚度、水合物分解程度的显著水平则远大于0.05，表明这3个因素对于斜坡安全系数的影响不显著。进一步比较各因素的显著性水平，可知对试验结果影响程度由强到弱依次为A（斜坡倾角）＞B（水深）＞E（分解程度）＞D（水合物层厚度）＞C（水合物层埋深），这与极差分析结果一致。

表5 方差分析表

4.3 边际均值、变化规律

图10为共计25种试验方案下的安全系数柱状图。从图10中可以看出，除个别试验方案外，绝大多数试验方案所得安全系数均在安全线以上，尤其是斜坡倾角3°时安全系数大于5，表明海底斜坡具有良好的稳定性。安全系数随试验方案的不同呈现较强的规律性，结合表3～5可知，图9的递减、递增规律分别由斜坡倾角和海水深度所引起，且这两个因素对安全系数的影响非常显著。当对不同因素水平下的边际均值进行求取时，就存在变化规律被斜坡倾角与海水深度所掩盖的可能性，这种误差是由于个别因素的异常显著性（Sig值）所引起的。因此，当需要对波动规律作进一步分析时，应首先排除异常显著性因素的干扰[17]。

图10 不同方案下的安全系数柱状图

对不同因素水平下的安全系数边际均值进行求取，获得安全系数变化规律（图11）。根据图11-a，安全系数与斜坡倾角呈负相关关系，随倾角的不断增加，安全系数的降低幅度逐渐减小，两者呈现类抛物线关系。倾角15°时，安全系数基本接近于安全线，海底斜坡处于临界稳定状态。将斜坡倾角与安全系数的关系进一步整理，分别以Fs、1/tanβ为坐标，得到图11-b，两者满足式（4）：

图11 各因素不同水平下安全系数变化规律图

式中Fs表示安全系数；β表示斜坡倾角，（）；k，b表示一次函数系数。根据式（4），安全系数与斜坡倾角正切值的倒数（1/tanβ）呈一次函数关系，并且式中b≈0，即安全系数与斜坡倾角正切值的倒数（1/tanβ）呈正比。这样通过坐标转换就将斜坡倾角与安全系数之间的非线性关系转变成了线性关系，同时表明斜坡倾角对安全系数的影响是通过倾角的正切值（tanβ）来体现的。

根据图11-c，安全系数与水深呈正相关关系，且单位水深增加所引起的安全系数增量为定值；由图11-d，安全系数与水合物层厚度、水合物层埋深、水合物分解程度的关系并不符合单调关系，而是随水平变化呈现一定波动。由之前图10的分析可知，这是由于斜坡倾角与海水深度的异常显著性所引起的，即水合物层厚度、水合物层埋深、分解程度对安全系数的作用效果被斜坡倾角与水深的误差所掩盖。

图12为在排除斜坡倾角、水深影响后，安全系数随分解程度、水合物层埋深、水合物层厚度变化规律图（倾角6 、水深800 m）。根据图12，安全系数随分解程度的增加单调递减，随水合物层埋深的增加单调递增，与水合物层厚度之间的关系则随水合物分解程度的不同而不同。由图12-b，当水合物分解程度不同时，安全系数与水合物层埋深之间基本为正相关关系，且随埋深的不断增加，安全系数增长幅度逐渐降低。因此预计，存在一个临界埋深，当埋深持续增长至大于临界埋深时，将基本不会对安全系数产生影响，即埋深对安全系数的影响是有一定限度的。

根据图12-c，当水合物分解程度不同时，安全系数与水合物层厚度之间的关系亦不同。分解程度较低时，安全系数与水合物层厚度之间为正相关关系，而分解程度较高时，两者为负相关关系。分析认为，这是不同分解程度下水合物储层与周围岩层之间的相对“力学差异性”所造成的。当分解程度较低时，其力学性质（力学参数）较周围岩层高，对海底斜坡具有“加固增强”作用；当分解程度较高时，其力学性质显著低于周围岩层，斜坡强度被“拉低”。因此，安全系数与水合物层埋深之间呈现出如图12-c所示的变化规律。