例谈“一题多变”在高中数学教学中的应用
2021-11-19汪爱爱
汪爱爱
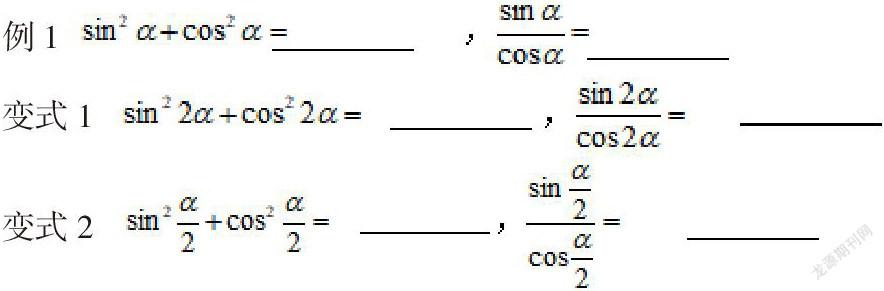

摘 要:高中数学内容较多且抽象,学生理解较为困难,因此会出现一听就会,一做就错,知识概念理解不透彻,应用不灵活等问题。本文将通过“一题多变”在“知识点、公式讲解”,“例题讲解”及习题练习过程中的应用进而有效解决上述问题。
关键词:一题多变; 高中数学
高中数学新课程标准指出: 培养和发展学生的数学思维能力是开发智力、全面培养数学能力的主要途径。因此,高中数学课程应该注重提高学生的数学思维能力,这也是高中数学教育的基本目标之一。学生如何学好数学?教师如何教好数学?这是很多教师,学生及家长一直关心和思考的问题。我认为教师要使学生学好数学,不是一味的题海战术,而是要以题目为载体激发其学习兴趣,促进其数学思维的行成与发展,提高其解决问题的能力,从而促进其全面发展。
我从教学中发现,一题多变是培养学生数学思维和方法的的有效手段。“变”是“一题多变”的关键和核心,“变”的精髓和价值在于求证“为何要变”、“如何去变”的过程,让学生在问题的认知、探索、发现、设计、解决、创造等方面进行全过程、全方位、深层次、主体性、实质性的参与,并从中获得对问题的深刻理解,从而体会万变不离其宗的本质,提高其数学思维能力,减轻学业负担,高效学习,成为学习主人[1]。下面就来谈谈我在教学中应用“一题多变” 的一些做法。
一、知识点讲解时采用一题多变,让学生理解更全面、更透彻
高中数学内容较多,数学概念、公理、定理及公式等内容比较抽象,学生理解起来比较困难得这将直接影响学生对相关问题求解的准确性与全面性。而“一题多变”式的讲解能够锻炼学生的数学思维,加深其对知识本质的理解,从而达到事半功倍的效果。
α为使得上述三角函数有意义的任意角。
上述变式使得学生深刻理解同角三角函数基本关系:同一个角α的正弦,余弦的平方和等于1,商等于角α的正切,而与α的具体取值没有关系;进一步加深理解,为后期公式的应用做好铺垫。
二、例题的讲解中采用一题多变,触类旁通,让学生融会贯通、活跃思维
高中教材中的例题相对较典型,但数量较多,如果在教学活动中出现太多题目则令学生眼花撩乱,使其陷入迷茫。因此,选择较为典型的例题,并改变题目中的已知条件转换为新的题型,不仅节省了大量阅读题目的时间,也能够大幅度降低高中学生的课业负担,最重要的是能够提升学生的思维能力和应变能力,让学生做到举一反三,灵活运用数学知识,提高对数学问题的分析能力以及解题能力。下面通过一个例题来说明一题多变在三角函数求值问题中的应用。
本例通过从已知和α所在的象限求的值,变化到已知不知α所在的象限求的值,再变化到已知求的值及含有代数式的值。使得学生会应用同角三角函数基本关系来知一求二,同时体会角α所在的象限对三角函数值符号的影响,巧妙避易错点。
三、一题多变在练习中的运用,让学生复习巩固、发散思维
在数学教学中,题海战术会让学生感到作业量太大。如果利用课本的习题,进行一些由简单到复杂、由易到难的演变,就不会让学生感到太难太多而无从下手甚至产生厌学情绪。经过这样长期的训练,学生的解题能力自然会不断提高,还能逐步发展他们的创新思维能力,在以后的练习或考试中即使遇到了未见过的新题也敢于尝试[2]。
注 在本例中通过了由只利用辅助角公式(或和差角公式)到先用降幂公式再用辅助角公式将所给函数恒等变化为。这种由浅入深的变化,使学生掌握了三角恒等变换的本质,进而对于类似问题也就有信心了。
四、結束语
综上所述,在高中数学教学中适当地采用“一题多变”,可以发散学生思维,能够极大地锻炼学生类推能力和归纳的能力,开拓学生视野,提高分析问题的能力,发展创造性思维。
参考文献:
[1] 张永平. 一题多变与一题多解在高中数学教学中的运用[J]. 教学论坛,2012,1(1):42.
[2] 王能华. 浅析“一题多变”在高中数学教学中的运用[J]. 安庆师范学院学报,2015,21(1):134-135.
