基于增强学习的工业机器人自主运动规划

刘景亚

（中冶赛迪技术研究中心有限公司智能机器人技术研究所，重庆，401122）

0 引 言

目前钢铁冶金行业面临资源和环境约束不断加强、人口老龄化、劳动力等生产要素成本不断上升等问题，各钢铁企业对降本、提质、增效需求迫切。工业机器人在钢铁冶金领域的应用有利于降低企业人力成本、生产维护成本和安全事故的发生，提高生产效率、工艺稳定性和产品质量。由于钢铁冶金流程非结构化的工作环境不确定性因素较多，故要求工业机器人具有更多的自主性和智能化程度。

增强学习是机器学习和智能控制领域的主要方法之一，关注的是智能体如何在环境中采取一系列行为从而获得最大的累积回报，是一种提高智能体的自主性和对环境适应能力的有效方法[1]。近年来，增强学习正在被越来越广泛地应用到机器人研究领域，如移动机器人路径搜索[2]、人形机器人步态规划[3]和多关节机器人控制[4]等。K.Shibata[5-7]等利用基于增强学习的TS算法，将视觉信号输入到神经网络，针对二自由度的机械臂进行了研究；A.A.Jafari[8]等将增强学习和自组织映射应用到机器人控制中，对二自由度机械臂的路径规划进行了研究；J.A.Martin和D.Maravall等[9-10]利用进化理论和增强学习建立了自主机器人通用的控制器，并且对多连杆机器人的运动学逆解问题进行了研究。

本文基于增强学习的Sarsa算法对应用在钢铁冶金领域的平面三自由度工业机器人进行研究，目的在于实现工业机器人的运动自主规划和在不确定工作环境中的自适应。首先，笔者建立了机器人自主运动规划模型；其次，研究了增强学习的Sarsa算法并编程实现；最后，利用仿真实验对模型进行了验证。

1 模型建立

1.1 任务描述

工业机器人在钢铁冶金领域具有十分广泛的应用，其运动规划功能在执行搬运、抓取等动作时尤为重要。传统的机器人运动规划通过人工示教或逆运动学计算求解。由于钢铁冶金环境的特殊性和任务可重复性不强，机器人在冶金流程应用时，传统运动规划方法效率低下且编程任务繁重。因此实现工业机器人的运动自规划和对不确定工作环境的自适应，将有利于机器人应用的推广。

本文研究中，机器人的任务可概括为以下两点：

1）在工作空间给定固定的目标点，机器人不依赖于人工示教和编程，通过自学习的方式到达目标点，实现运动路径的自主规划；

2）在工作空间随机给定目标点，机器人仍可通过自主规划的方式到达目标点。

1.2 机构运动模型

平面三自由度工业机器人的机构运动模型如图1所示。以工业机器人的底座中心O为原点，建立直角坐标系XOY。简化的运动模型中，机器人由连杆OA、连杆AB和连杆BC组成，假设三个连杆的杆长分别为L1、L2和L3，三个连杆之间的夹角分别为θ1、θ2和θ3，末端执行器的位置和姿态由C点坐标（xT，yT）和向量BC与X轴正方向的夹角φT来表示。

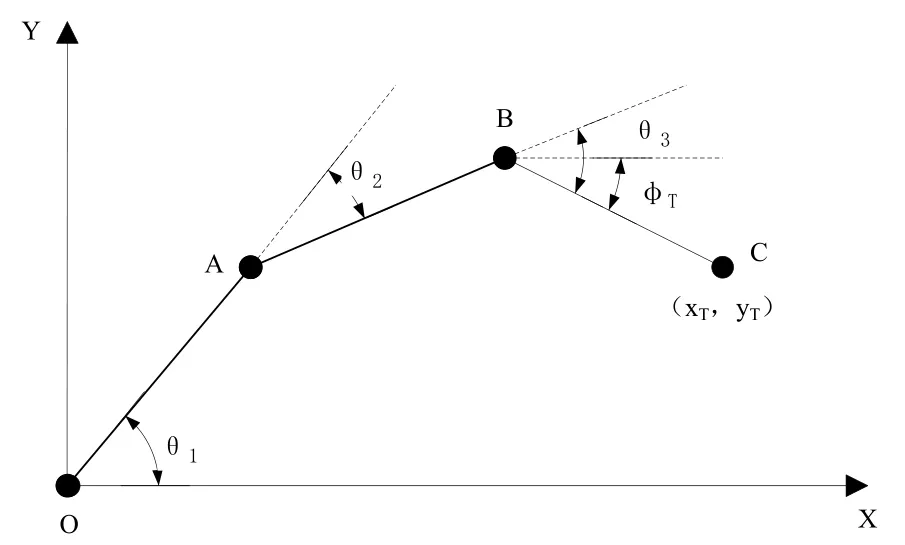
图1 机构运动模型

运动规划的目的为，已知目标点的位置，求解一系列满足期望要求的θ1、θ2和θ3，以使末端执行器到达目标位置。

根据几何关系，则有：

1.3 自主运动规划模型

根据马尔科夫决策过程的特点，笔者建立的自主运动规划模型如图2所示。

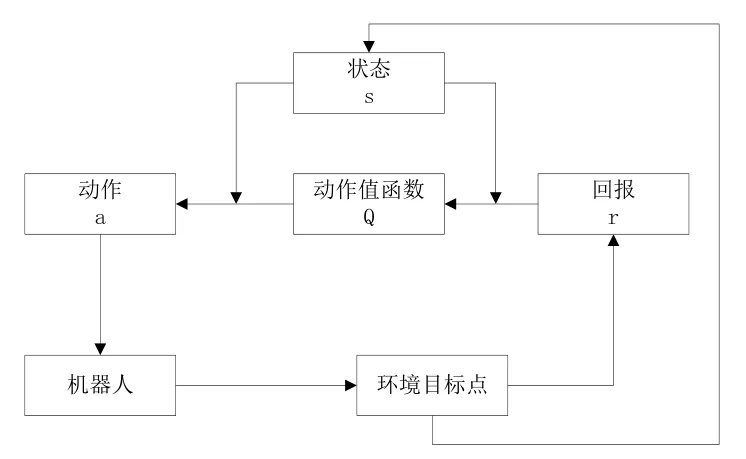
图2 自主运动规划模型

当目标位置给定后，自主规划模型根据当前的状态s和任意初始化的动作值函数Q选择动作a；该动作驱动机器人运动；外部环境对机器人的动作进行评价，给出回报函数r，同时改变状态s；根据回报函数r和更新的状态值对动作值函数进行更新；根据更新的状态s和动作值函数Q，再选择动作a。

上述过程进行迭代循环，使机器人采取一系列行为，从而获得最大的累积回报，并选择最优的策略使机器人自主到达目标位置。

上述建立的自主运动规划模型采用Sarsa算法实现，该算法是增强学习中的常用算法，经常用于决策控制问题中。该算法估计的是动作值函数，在下面任意状态s上所有可执行的动作a的动作值函数Q（s,a）。对于每个非终止的状态st，在达到下一个状态后，根据公式更新动作值函数Q（st,at），最终得到所有“状态—动作”对的动作值函数，并根据得到的动作值函数输出最优策略π。

动作值函数的更新公式如下：

Sarsa算法的流程如图3所示。其中，Epsiode表示学习次数，MaxEpsiodes表示最大学习次数，Step表示学习中的迭代步数，MaxSteps表示学习中的最大迭代步数。

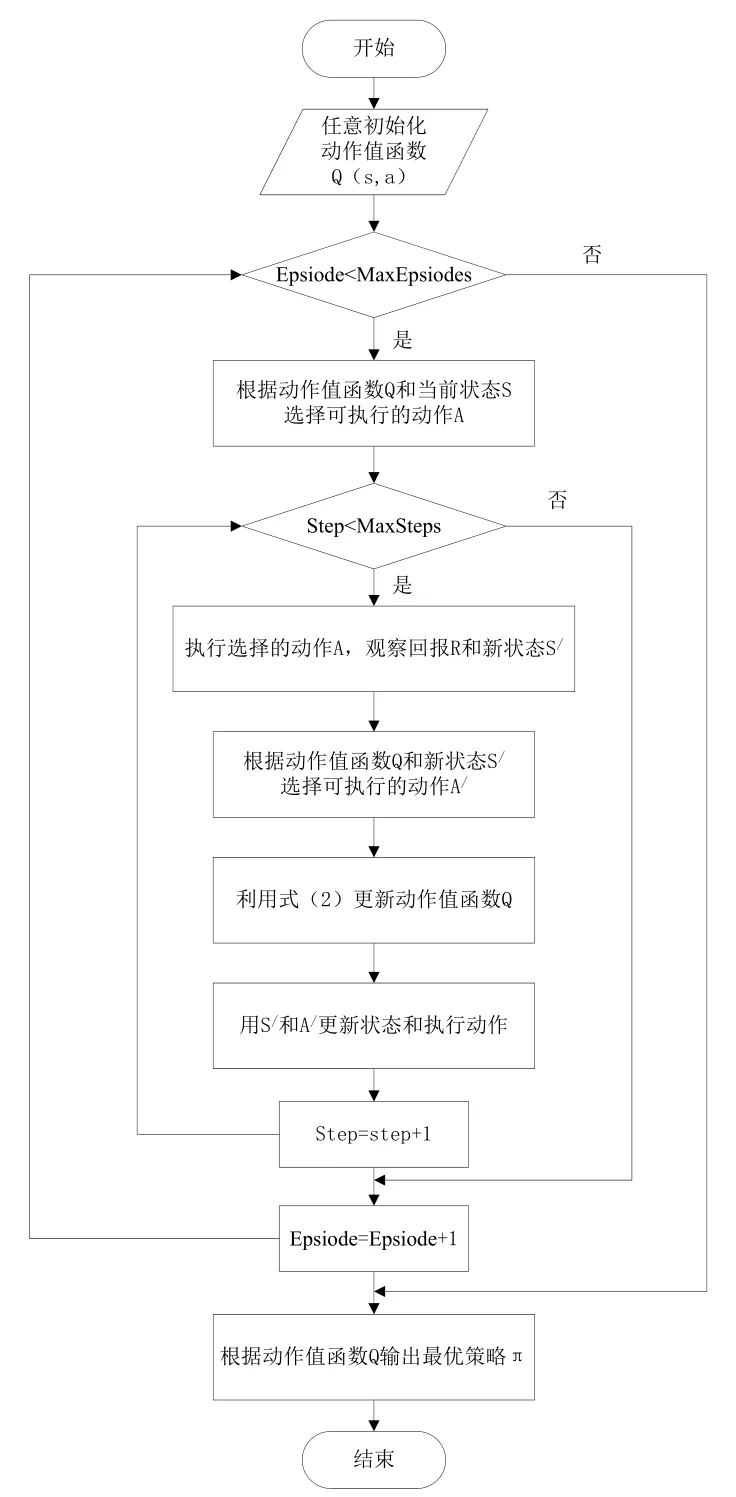
图3 算法流程图

2 仿真验证

笔者针对一个具体的算例进行仿真，对自主运动规划模型进行验证。平面三自由度工业机器人的具体几何参数如下：L1=8.625cm；L2=8.625cm；L3=6.125cm。

下面是仿真结果及分析。

图4和图5是目标位置固定的情况，机器人末端执行器的起始点坐标为（0,23.4），目标点坐标为（20,3）。图6、图7和图8是目标点为随机位置的情况，机器人末端执行器的起始点坐标仍为（0,23.4），目标点位置每次学习中随机确定。

图4 固定目标学习结果

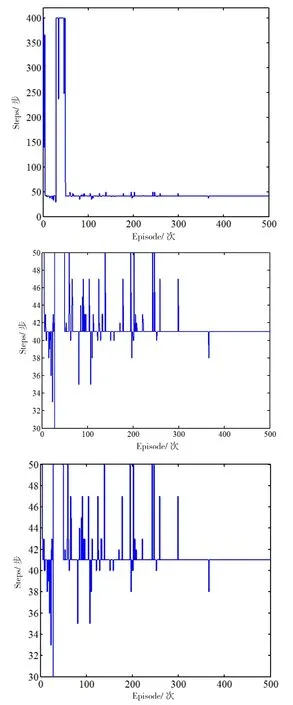
图5 固定目标学习步数

图6 随机目标学习步数

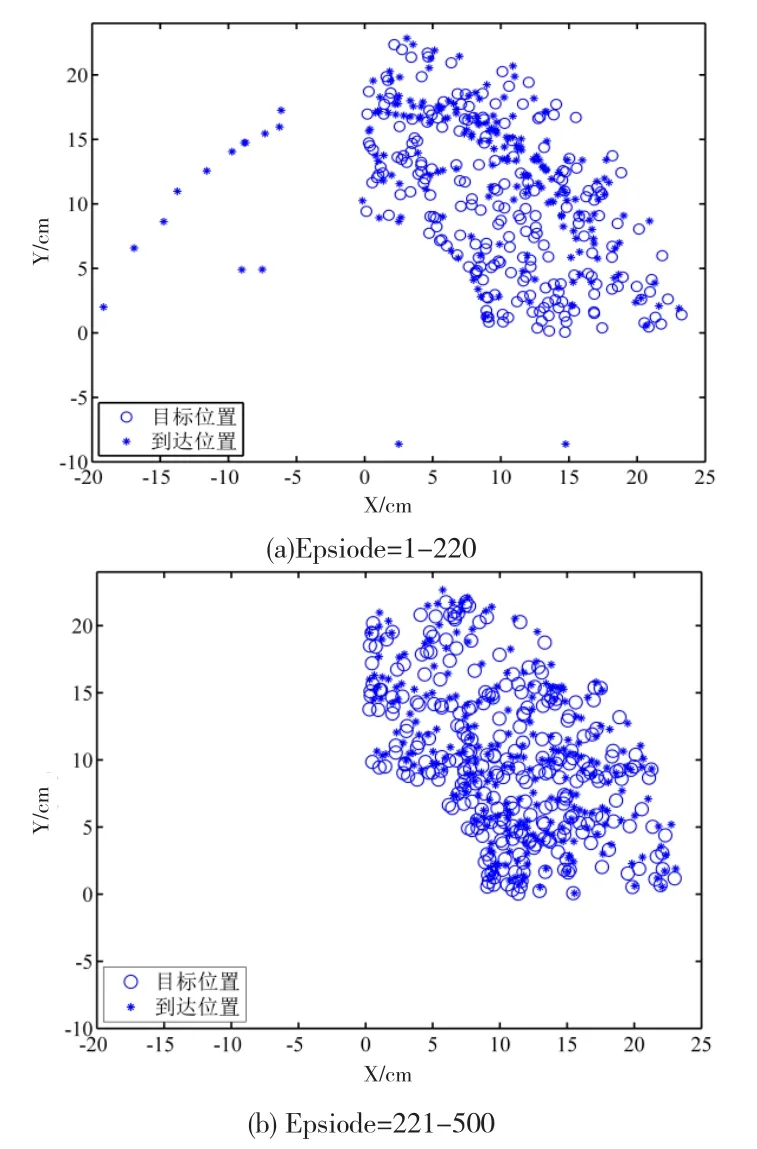
图7 随机目标学习结果

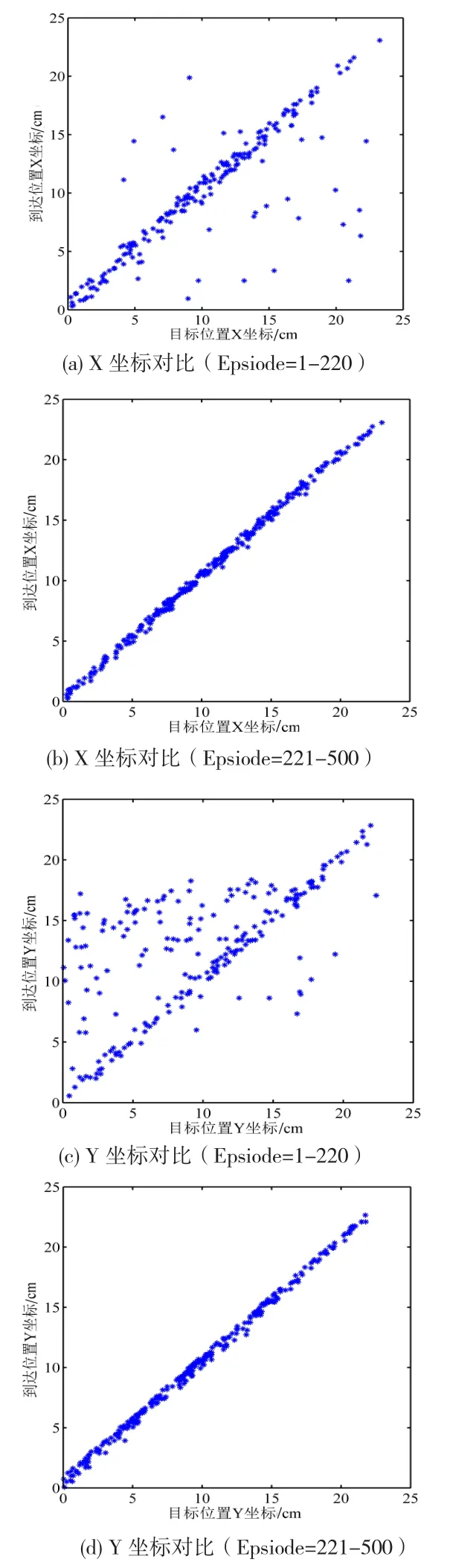
图8 随机目标学习效果对比

图4是目标位置固定时不同学习次数的学习结果。图4(a)为经过1次学习的情况，可以看出运动路径曲折，绕过目标点后再折回，并且在临近目标位置时存在振动；图4(b)为经过10次学习的情况，可以看出运动路径已经比较光滑柔顺，但在临近目标位置时仍存在振动；图4(c)为经过100次学习的情况，可以看出运动路径已经非常光滑并且运动轨迹也有优化，在临近目标位置时振动已经完全消除。

图5为经过不同的学习次数达到固定目标位置所用的步数。由图5可以看出，随着学习次数的增多，达到目标位置所需的步数越来越少。在开始阶段，经过400步还没达到目标位置，学习是失败的；随着学习的进行，都可以在400步以内达到目标位置，学习能够成功，但所需要的步数还较多；经过300次学习以后，稳定在41步即可学习成功，达到目标位置。

由图4和图5可知，机器人可以根据自主运动规划模型，通过自学习和不断试错的方式达到固定的目标点。

图6为经过不同的学习次数达到随机目标位置所用的步数。由图6可以看出，在1-220次的学习过程中，要达到目标位置所需的步数较多，其中很多未能在400步以内达到目标位置，学习失败；在221-500次的学习过程中，达到目标位置所需的步数变小，每次都可以学习成功，达到目标位置的步数在100步以内。

图7是随机目标位置学习结果图，图7（a）是1-220次学习过程中机器人达到位置与目标位置的对比图，图7（b）是221-500次学习过程中机器人达到位置与目标位置的对比图。由图7（a）可知，到达位置与目标位置重合度不高，且部分的到达位置与目标位置相距较远；根据计算结果，距离偏差值从0.05cm到32.61cm，中值为2.52cm，标准差为6.70cm。由图7（b）可知，到达位置与目标位置重合度非常高；根据计算结果，距离偏差值从0.04cm到1.00cm，中值为0.84cm，标准差为0.18cm。即经过不断学习，机器人都可以在较少的步数内到达目标位置，实现成功学习。

图8是随机目标学习效果对比图，图8（a）和（c）是1-220次学习过程中机器人到达位置和目标位置的X和Y坐标图，图8（b）和（d）是221-500次学习过程中机器人到达位置和目标位置的X和Y坐标图，在上述图中如果到达位置和目标位置重合，图中的标记点应该分布在对角直线上。

在1-220次的学习过程中，根据仿真计算结果目标位置与实际到达位置X坐标的偏差值从-10.82cm到32.61cm，中值为-0.22cm，标准差为6.49cm；Y坐标的偏差值从-15.96cm到19.67cm，中值为-0.71cm，标准差为5.15cm；由图8可知，无论是X坐标图还是Y坐标图都比较离散，表明机器人到达位置和目标位置重合度较低。

在221-500次的学习过程中，根据仿真计算结果，目标位置与实际到达位置X坐标的偏差值从-0.99cm到0.55cm，中值为-0.44cm，标准差为0.26cm；Y坐标的偏差值从-0.99cm到0.52cm，中值为-0.64cm，标准差为0.28cm；由图8可知，无论是X坐标图还是Y坐标图都比较集中，密集分布在对角直线上，表明机器人到达位置和目标位置重合，说明机器人经过学习，在不断地自我进化，逐渐掌握运动自主规划的能力。

由图6、图7和图8可知，当目标点为随机值时，机器人仍可根据自主运动规划模型达到目标点，所需要的学习迭代次数比固定目标位置时多。

3 结 论

基于增强学习的Sarsa算法，本文首先根据工作任务要求，建立了平面三自由度工业机器人的自主运动规划模型。其次，本文利用仿真实验对自主运动规划模型进行了验证：当目标点为固定值时，机器人可以通过自学习、不断试错的方式到达目标点；当目标点为随机值时，机器人仍可以通过自主规划方式到达目标点，所需要的学习迭代次数比固定目标位置多。

研究结果表明，基于增强学习，工业机器人可以实现在不确定工作环境中的自规划和自适应，这将有利于工业机器人在钢铁冶金等非结构工作环境中的应用。