多类型元件混合直流电网机电暂态建模仿真*

徐攀腾 朱 博 喻文翔 宋述波 李建勋 樊友平

(1. 中国南方电网有限责任公司超高压输电公司广州局 广州 510500；2. 武汉大学电气与自动化学院 武汉 430072)

1 引言

基于电压源型换流器的柔性直流输电(Voltage source converter based high voltage direct current transmmission, VSC-HVDC)具有有功/无功解耦控制、无换相失败等方面的优势，能够弥补传统直流输电的部分缺陷。模块化多电平电压源型换流器(Modular multilevel converter, MMC)是VSC 拓扑结构中的一种，具有很好的发展前景[1-4]。受全控功率半导体器件容量的限制，在相当一段时间内VSC-HVDC 还不能满足远距离大容量电力输送的要求[5]。因此，由技术较为成熟的电网换相换流器(Line commutated converter, LCC)与电压源型换流器构成的混合直流电网成为未来直流网络的一种新的表现形式[6-8]。由于混合直流电网同时具备电网换相换流器和电压源型换流器的优势，受到工程和学术界的广泛关注，为分析和研究服务的直流电网建模仿真技术也成为了研究的热点[9-11]。

传统的电力系统仿真模型和工具并不能满足直流电网应用的需要[12]。文献[13-14]提出LCC-MMC两端混联直流输电系统，搭建数学模型，设计控制策略。文献[15]基于基尔霍夫定律分割系统导纳阵，提出超大规模MMC 电磁暂态提速模型。文献[16-17]基于状态矩阵节点法，采用CPU 和FPGA并行计算技术，实现MMC 的实时和超实时仿真。这些研究主要集中在电磁暂态领域，在日趋于电力电子化的电力系统背景下，大量开关器件的使用极大地限制了电磁暂态仿真的速度和规模。目前而言，电磁暂态仿真并不适合用于大规模交直流电力系统的暂态稳定分析与计算[10]。

对混合直流系统的机电暂态建模研究的文献较少。文献[5]构建了适用于大型电力系统暂态稳定计算的LCC-MMC 型混合直流电网的机电暂态模型。文献[18]研究了多端直流输电系统的通用建模方法，并且提出了多端直流输电系统中各换流站间的协调控制策略。文献[19]提出了一种考虑多种控制方式以及换流变压器变比的混合多端直流输电系统交替迭代潮流计算方法。文献[10]提出了改进的LCC-MMC 型混合多端直流系统潮流计算和机电暂态建模方法。然而，上述文献主要针对LCC-MMC 型混合多端直流系统，实际混合直流电网中的元件类型更多，需要更加系统全面地对其进行机电暂态建模。

为此，本文详细介绍了VSC 的两电平或三电平拓扑结构以及模块化多电平拓扑结构的机电暂态模型，同时建立了DC/DC 变压器和串联VSC 换流器等值模型，提出了混合直流电网中不同类型换流器的控制系统模型。从而提出了更为全面的混合直流电网机电暂态建模方法，并通过对算例在不同工况下的仿真对比分析验证了所建立机电暂态模型的可靠性，仿真计算的速度得到显著的提高。

2 混合直流电网机电暂态模型建立

直流电网由VSC 换流站、LCC 换流站、DC/DC变压器、直流线路等元件构成，如图1 所示。

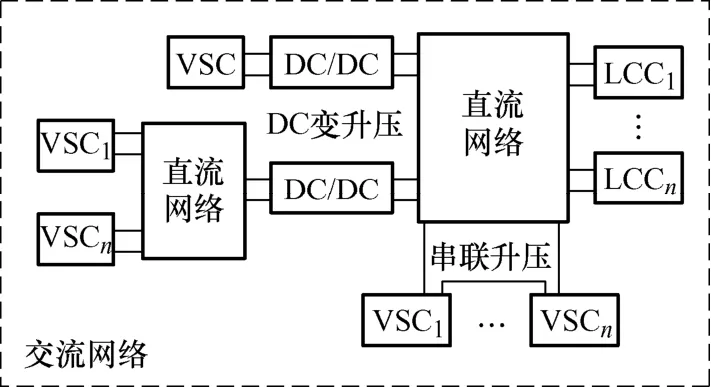
图1 直流电网示意图

2.1 LCC 换流站机电暂态模型建立

2.1.1 LCC 交流侧机电暂态等值模型

在系统对称平衡运行的条件下，LCC 作为整流站和逆变站的交流侧运行特征变量计算形式相同，LCC交流侧等值电路模型可以用以下代数方程组描述，图2 为LCC 作为整流站时的交流侧模型[2]。

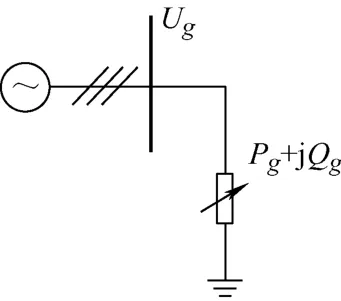
图2 LCC 交流侧模型(整流站)

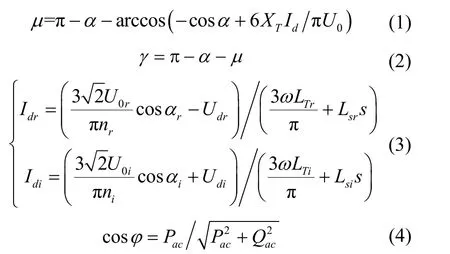
式中，α为LCC 的延迟触发角；μ和γ分别为LCC的换相角和关断角；P ac和Qac分别为LCC 的有功功率和无功功率；cosφ为功率因数；Ud和Id分别为直流电压和直流电流；U0为换流母线的线电压有效值；XT为LCC 等值压降阻抗。

LCC 的交流侧等效电路为代数方程描述的可变功率支路，需要用注入电流源来表示，具体的电流计算表达式可以参考文献[5, 10, 20-21]。

2.1.2 LCC 直流侧机电暂态等值模型

LCC 直流侧机电暂态等值模型如图3 所示。

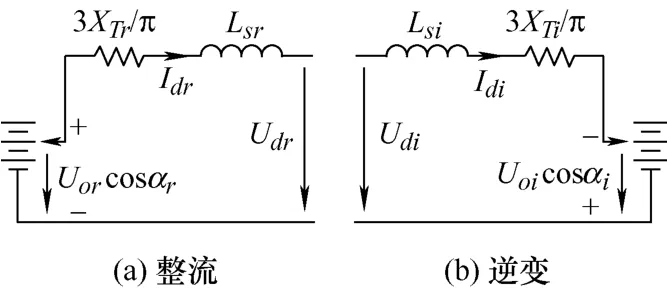
图3 LCC 直流侧机电暂态等值模型

LCC 作为整流站和逆变站可分别用以下代数方程来描述

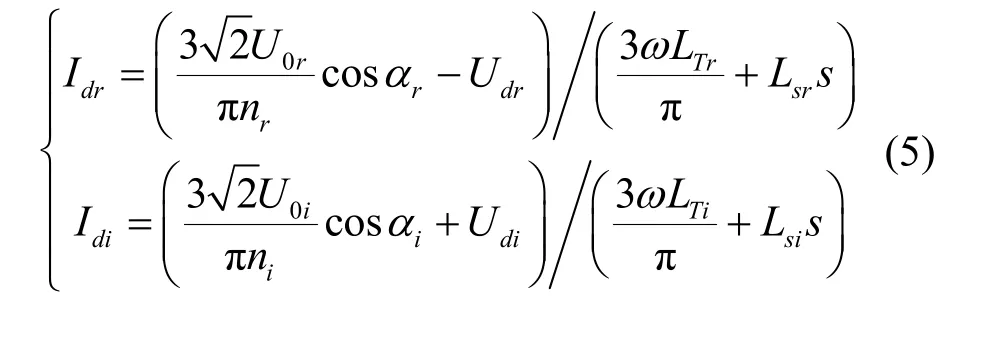
式中，r表示LCC 作为整流站；i表示LCC 作为逆变站。Lsr和Lsi分别为LCC 作为整流站和逆变站时平波电抗器的电感；L Tr和LTi为LCC 等值压降电感。

2.2 VSC 换流站机电暂态模型建立

2.2.1 VSC 交流侧机电暂态等值模型

在交流侧，VSC 换流器等效为幅值与相位可控的电压源，其与系统接口节点之间一般通过联结变压器与相电抗串联连接，存在无滤波器和有滤波器两种形式。

(1) 无并联交流滤波器

MMC 是典型的较高电平数VSC 换流器，无并联交流滤波器，其单相电路结构如图4 所示。

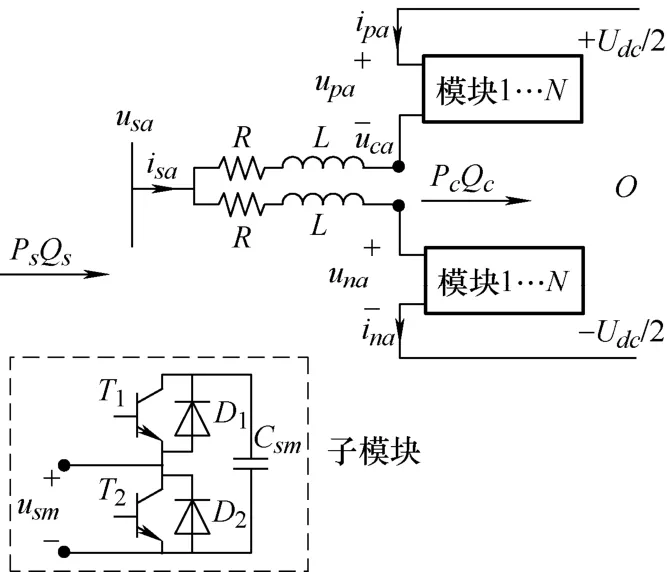
图4 MMC 型换流器模型结构图

设桥臂电阻、电感分别为R、L；接口节点电压分别为usa、usb、usc；换流器注入电压分别为uca、ucb、ucc；支路电流分别为isa、isb、isc。以交流到直流为功率正方向，接口节点有功和无功功率分别为Ps、Qs，换流器节点功率分别为Pc、Qc。

MMC 换流器外特性电压方程为

(2) 有并联交流滤波器

有交流滤波器时VSC 换流器模型如图5 所示。

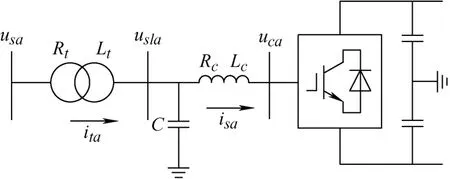
图5 VSC 模型示意图

设联结变压器二次侧节点电压分别为usla、uslb、uslc；变压器支路电流分别为ita、itb、itc；相电抗支路电流分别为isa、isb、isc；变压器忽略励磁支路，采用电阻与电感串联；滤波器等效电容为C。同样忽略交流侧等效电路的暂态过程，可得到交流侧等效稳态模型为

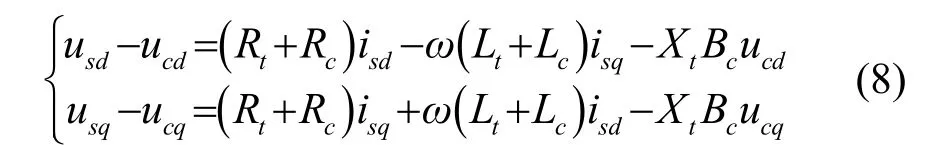
由式(7)和式(8)可以得到VSC 换流器交流侧机电暂态通用模型结构如图6 所示。当VSC 换流器交流侧无并联滤波器时，去掉电压uc的交叉耦合项，如图6 中虚线框所示。2.2.2 VSC 直流侧机电暂态等值模型

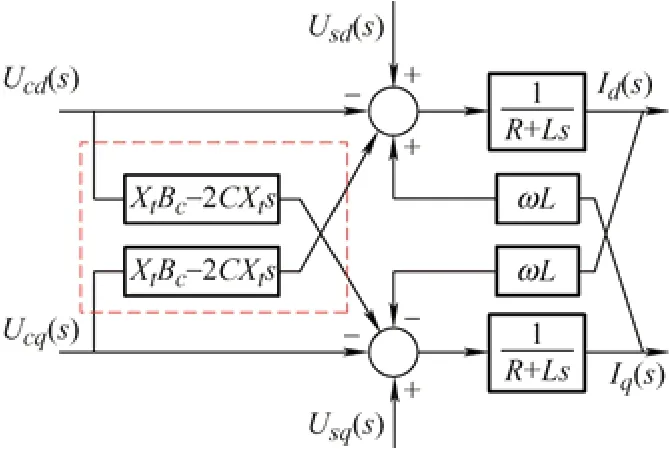
图6 VSC 换流器交流侧机电暂态通用模型结构

VSC 换流器在直流侧等效为受控的电流源，其等效模型如图7 所示。

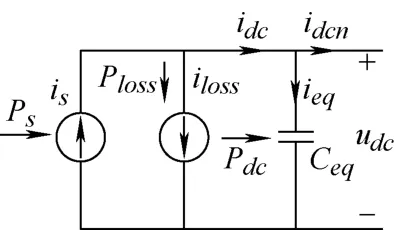
图7 VSC 换流器直流侧等效模型示意图

VSC 换流器的损耗采用等效电流源iloss表示，电流正方向与is正方向相反。R为损耗等效电阻，交直流侧功率平衡方程如下

式中，SP是交流侧注入功率；Pdc是注入直流网络的功率；Ploss是换流器等效损耗。

由图7 可列出集中电容接入换流器的直流侧数学模型

式中，idcn是换流器注入直流网络的电流；Ceq是等效电容。

对于MMC 结构的VSC 换流器，电容为分散式

连接方式，忽略阀组结构，在直流侧采用一个等效的集中电容来模拟分散连接的电容，即

式中，N为桥臂中的子模块个数；Csm为子模块电容大小。

2.2.3 功率方程

VSC 换流器直流侧等效模型中，受控电流源可以表示交流向直流注入的功率大小，理想情况下忽略换流器阀组的开关损耗，可列出标幺化的功率方程为

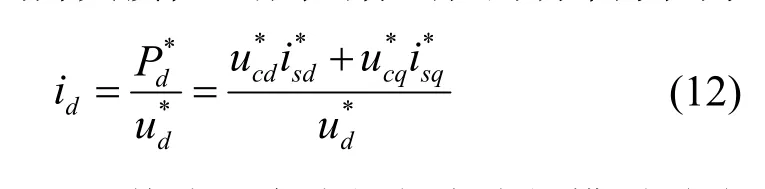
功率方程为VSC 换流器交流侧与直流侧模型联结的纽带。

2.2.4 串联VSC 换流器等值模型

直流电网中，为达到与LCC 换流器电压和容量匹配的目的，可串联VSC 换流器单元。以N单元串联为例，串联VSC 换流器机电暂态等值模型如下。

(1) 交流侧采用倍乘等值方法

式中，isd′ 、isq′ 是等值注入电流；Ceq′ 、R′分别是等值电容、电阻。

2.3 DC/DC 变压器机电暂态模型建立

多电压等级是直流电网的特征之一，将不同电压等级的直流输电线路互联，可采用DC/DC 变压器。本文基于外特性等值的方法，提出DC/DC 变压器的机电暂态等值模型，如图8 所示。

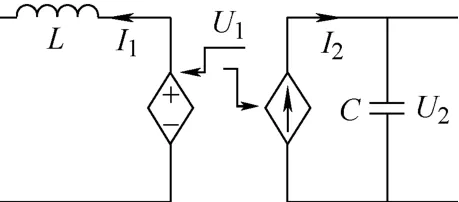
图8 DC/DC 变压器外特性等值模型

DC/DC 变压器机电暂态等值模型由可控电压源U1和电流源I2组成。可控电压源的直流电压由所连接直流网络的运行电压决定，可控电流源I2的数值通过支路有功功率和电压U2的量测值计算得出。

2.4 直流网络机电暂态模型建立

直流网络是各VSC 换流站、LCC 换流站、DC/DC 变压器之间的重要纽带。在直流电网机电暂态仿真计算时，直流网络模型是微分方程，其求解方法有别于交流网络相量模型的求解方法。任意拓扑形式的直流网络，指的是站与站之间的直流线路可任意相连，同时直流网络可以存在与换流站没有直接联系的联络节点。相应的微分方程列写如下。

(1) 对于第i个直流节点

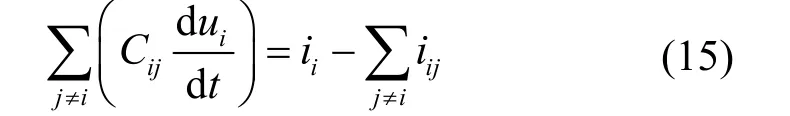
式中，Cij和iij分别为与节点i相关联的第j条支路的电容和电流；ui为第i个节点的直流电压，若该节点直接与LCC/MMC 直流侧电路相连接，则ii为LCC/MMC 直流侧电路馈入的直流电流，否则对于直流网络的中间联络节点，ii= 0。

(2) 对于第ij条支路

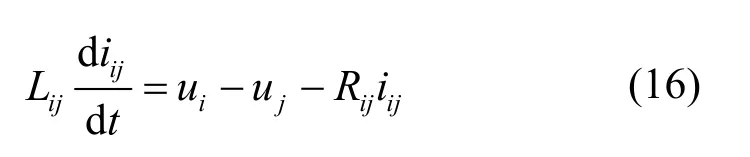
式中，Rij和Lij分别为第j条支路的电阻和电感；uj为第j个节点的直流电压。

直流线路的单π 集中参数模型如图9 所示。

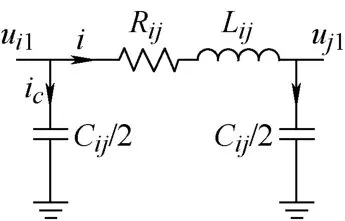
图9 直流线路单集中参数等值模型

3 换流器控制系统模型

3.1 LCC 换流控制器

通用的LCC 换流控制框图如图10 所示。LCC换流器是整流状态时，只有定电流控制起作用，触发角需要满足α＞αmin；LCC 换流器是逆变状态时，可以选择定电流控制或定熄弧角控制，也可以将定电流控制作为定熄弧角控制的后备控制方式，电流裕度一般取额定电流的10%[12]。

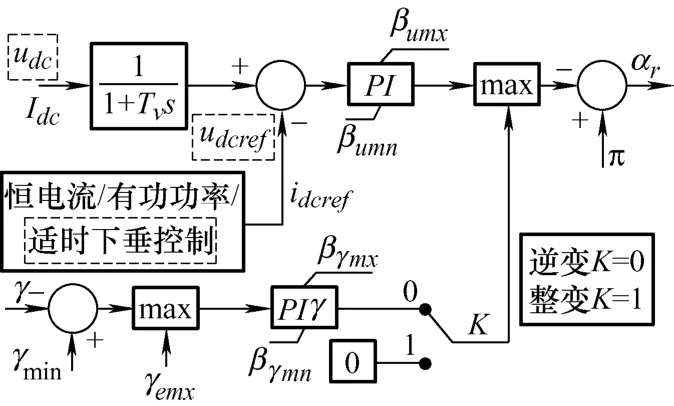
图10 LCC 换流器通用控制器框图

3.2 VSC 换流控制器

VSC 换流控制器可分为外环控制和内环控制。外环控制主要包括有功功率控制、直流电压控制、直流电压裕度控制、无功功率控制和交流电压限幅控制。内环控制为电流闭环控制，接受外环所计算的dq轴电流指令，计算换流器的注入电压。

3.2.1 外环控制

有功功率控制和直流电压控制均采用闭环的PI控制，直流电压裕度控制输入的直流电压指令udcrefh、udcrefl是与额定值一定存在偏差的电压裕度值，以实现当直流电压超标时限幅的作用。无功功率也采用闭环的PI 控制，交流电压限幅控制的原理与直流电压裕度控制类似，当母线电压超出范围时，交流电压限幅控制将启动，取得无功功率的控制权，从而稳定交流电压。

3.2.2 内环控制

内环控制控制策略依然为PI 控制。采用带有电流偏差的闭环控制模拟支路压降，能够实现正确的控制特性，如下所示

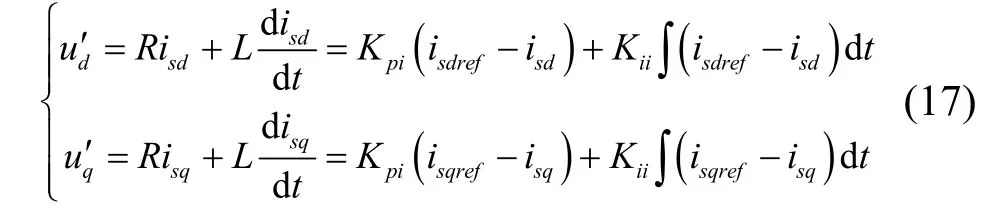
4 仿真验证

4.1 算例设计

为验证本文提出的混合直流电网机电暂态模型的准确性与快速性，设计了如图11 所示的四端混合直流电网。在PSCAD V4.5 中搭建了该仿真算例的电磁暂态模型，仿真步长是2 s，在PSS/E 中搭建了相应的机电暂态模型，仿真步长是1 ms。混合直流电网仿真系统的基本参数如表1 所示。混合直流电网仿真系统采用的控制策略如表2 所示。混合直流电网仿真系统的初始潮流如表3 所示。

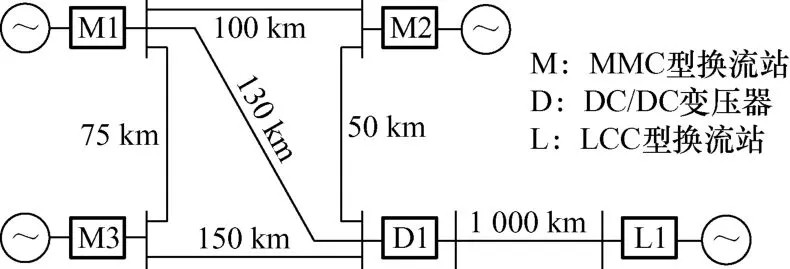
图11 四端混合直流电网示意图

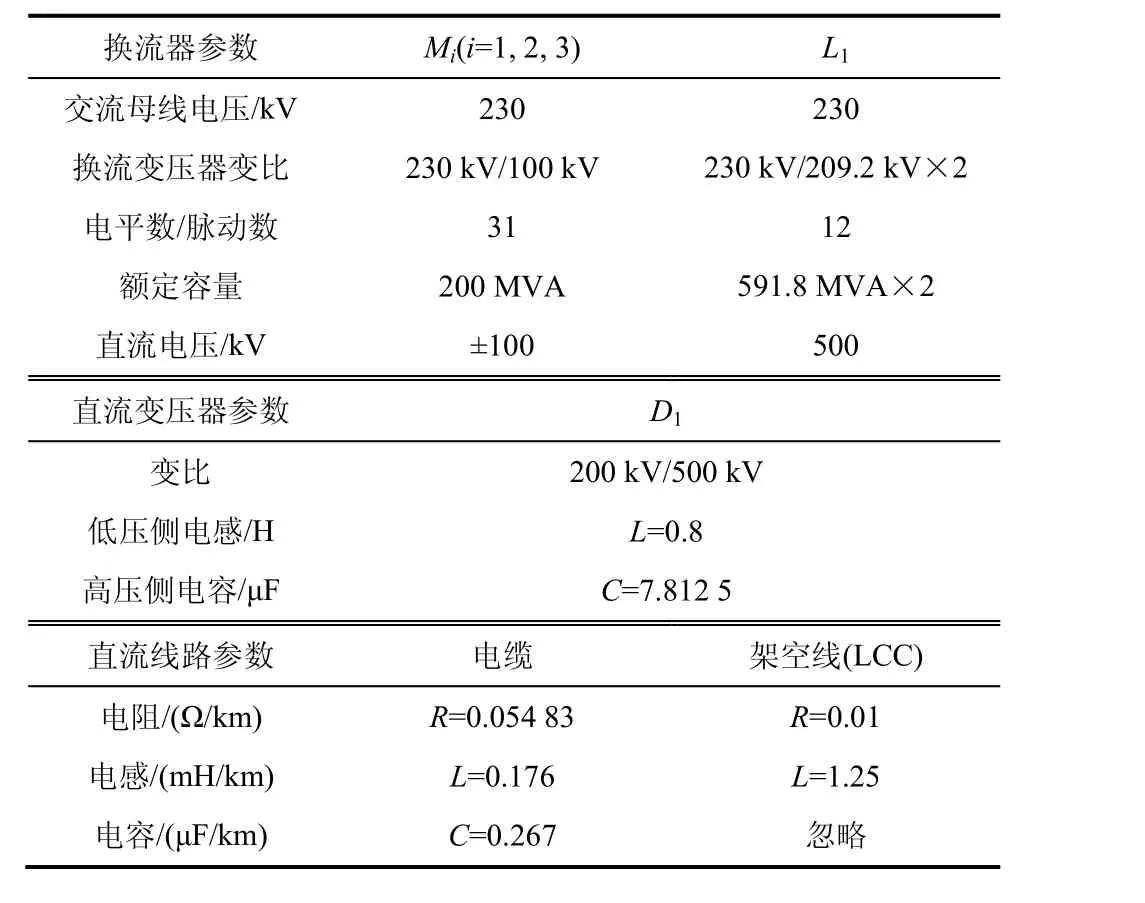
表1 混合直流电网仿真系统基本参数

表2 混合直流电网仿真系统控制策略

表3 混合直流电网仿真系统初始潮流

4.2 仿真结果对比分析

分别针对3种工况进行电磁/机电暂态仿真结果对比和适时下垂控制过程的分析。

4.2.1 直流电网内有功功率不平衡

站D1 功率参考值在0.1 s 由400 MW 阶跃到470 MW，支路D1L1 传输功率经过短暂的暂态过程控制到470 MW，如图12a 所示。直流电网功率缺额导致站M1、站D1 直流电压暂态下降，如图12e、12f 所示。站M1 控制直流电压，注入功率经过短暂的上冲，稳态控制到220 MW，站M2、M3 处于恒功率运行区间，稳态功率分别为210 MW 和160 MW，分别如图12b、12c、12d 所示。图12 中的电磁暂态仿真曲线和机电暂态仿真曲线基本吻合。表4 为暂态过程后的潮流分布表。电磁暂态仿真耗时3 084.66 s，机电暂态仿真耗时2.21 s，直流电网机电暂态模型可显著提高仿真速度。

图12 直流电网内有功功率不平衡仿真对比

表4 功率不平衡暂态过程前后潮流分布

4.2.2 直流电网拓扑变化

直流线路M2D1在0.5 s断线，功率瞬间降为零，直流电网潮流重新分布。仿真对比结果如图13 所示。经过短暂的暂态过程，支路M1M2、M1M3、M1D1、M3D1 的功率变化如图13a～13d 所示。支路D1L1 依然能够按恒功率400 MW 运行，如图13e 所示。由于直流网络潮流加重，导致网络损耗增加，站M1 注入有功功率变化如图13f 所示。

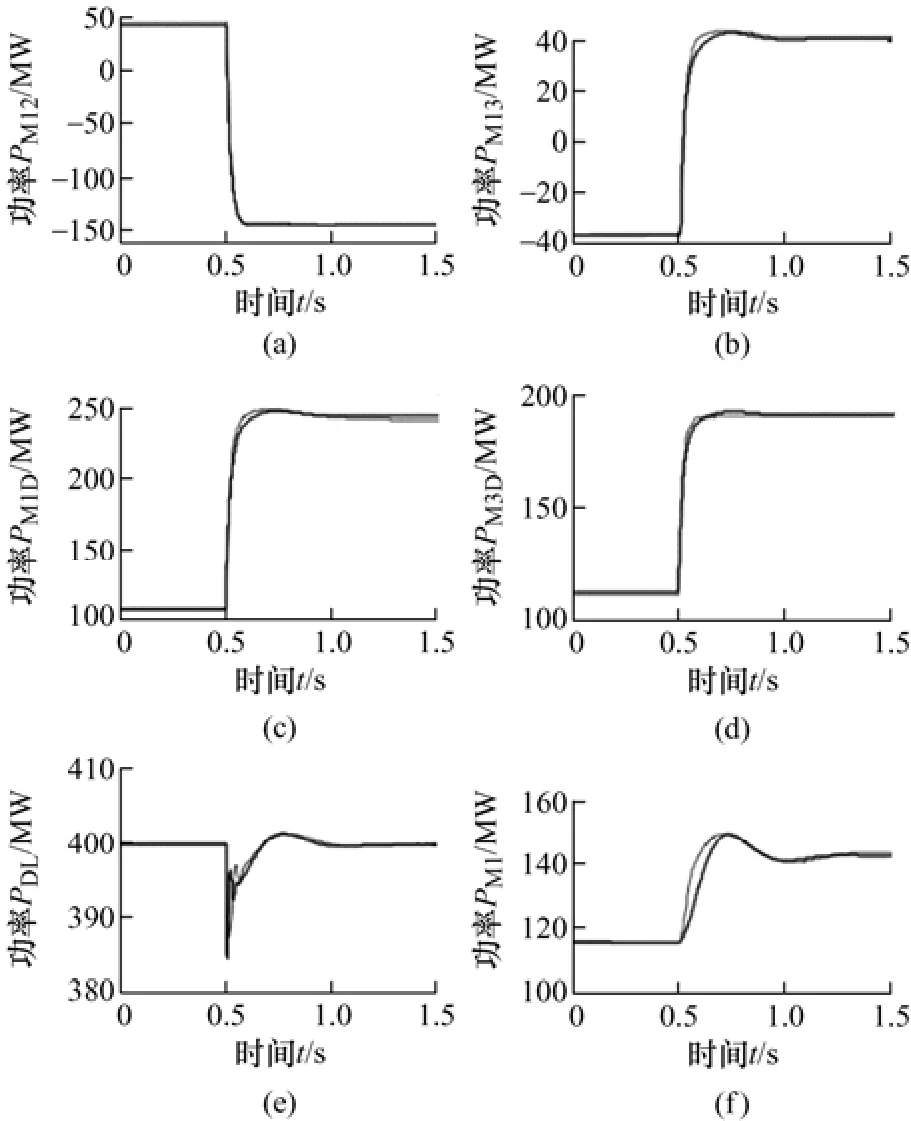
图13 直流电网拓扑变化仿真对比曲线(功率)

潮流重新分布导致直流母线电压发生变化，仿真对比结果如图14 所示。站M1 能够控制母线M1恒电压200 kV 运行，如图14a 所示。断线前后，母线M2、M3 的电压变化如图14b、14c 所示。站L1受扰前后的电压不变，如图14d 所示。表5 为暂态过程后的潮流分布表。

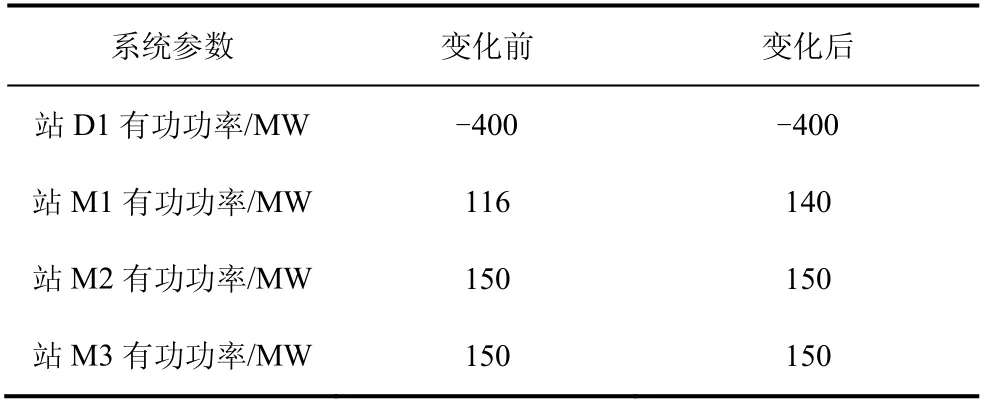
表5 系统拓扑变化暂态过程前后潮流分布

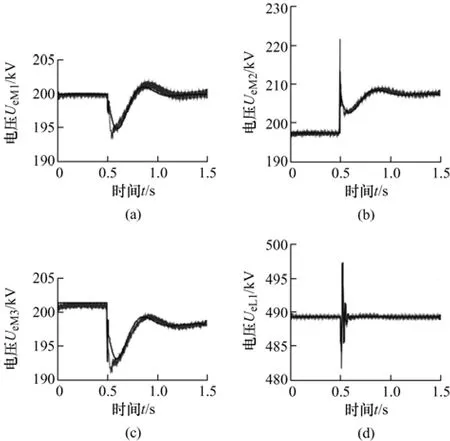
图14 直流电网拓扑变化仿真对比(电压)

电磁暂态仿真的曲线与机电暂态仿真的曲线基本一致。该工况电磁暂态仿真耗时2 407.22 s，机电暂态仿真耗时1.80 s，速度得到明显提升。

4.2.3 交流系统短路故障

站M1 换流变压器低压侧在0.5 s 发生三相接地短路故障，持续0.1 s。仿真对比结果如图15 所示。在故障前后，支路D1L1 保持恒功率389.6 MW，站L1 保持恒电压489.6 kV 运行。电磁与机电暂态仿真曲线基本吻合。该工况电磁暂态仿真耗时2 320.83 s，机电暂态仿真耗时1.97 s，仿真速度得到明显提升。

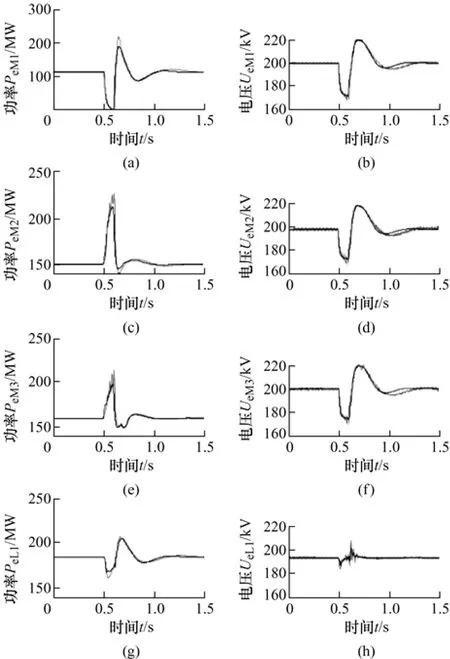
图15 交流系统短路故障仿真对比

3 种工况下电磁/机电暂态仿真耗时情况如表6所示，可以看出本文所提建模方法在仿真速度方面具有较大优势。

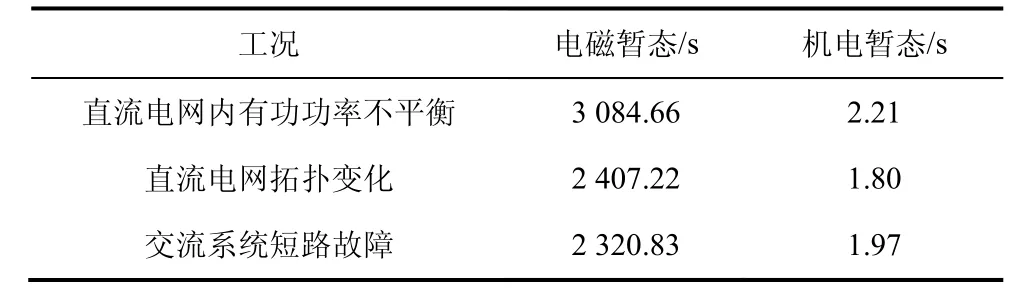
表6 电磁/机电暂态仿真耗时对比

5 结论

本文研究了包含DC/DC 变压器的LCC-VSC 混合直流电网的机电暂态模型建立方法。根据换流器基本数学模型和机电暂态仿真的特征，合理简化后提出直流电网基本元件的机电暂态模型。首先简述了LCC 换流器的机电暂态模型；随后分析较低电平数VSC 换流器和MMC 换流器的数学模型，提出了VSC换流器通用的机电暂态模型结构和参数等值方法，交流侧用交流电压源和集中电感等值，直流侧用直流电流源和集中电容等值；最后，基于外特性等值方法，提炼出DC/DC 直流变压器的机电暂态模型。设计了四端混合直流电网的仿真算例，分析不同工况下的运行特性。

电磁/机电暂态仿真对比表明，本文提出来的混合直流电网机电暂态建模仿真方法准确、可靠，仿真计算的速度得到显著的提高。