变流器交流电流直流成分抑制策略与设计*

俞 斌 谢 民高 博孙 辉 丁津津 张 峰王鹏肖华锋

(1. 国网安徽省电力有限公司 合肥 230001；2. 国网安徽省电力有限公司电力科学研究院 合肥 230601；3. 东南大学电气工程学院 南京 210096)

1 引言

非隔离并网逆变器(Transformerless inverter,TLI)由于其高效率、小体积、低成本等特性在分布式光伏并网系统中得到大量应用[1]。但同时，由于取消了连接至并网公共连接点(Point of common coupling，PCC)的工频变压器，进而失去了“变压器隔直”这一屏障，使得进网交流电流中可能存在直流成分[2]。该直流成分将引起一系列危害，如PCC上级变压器饱和、电缆腐蚀、计量误差等[3]。

为了促进TLI 应用和保证各电气设备安全可靠运行，各国并网标准对直流成分均提出了严格的指标限制[3]，如表1 所示。

表1 几种典型并网标准中的直流分量指标

引起直流成分的原因主要有功率器件的特性差异、门极驱动电路不对称、电流传感器的测量误差、信号调理电路和模数转换引入的直流偏差等[4]。

为了防止这些因素引起的直流成分超过并网标准规定的限值，一些有效的抑制措施被相继提出，大致可以分为三类，即检测反馈法、电容隔直法和智能算法。一般来讲，检测反馈法需要额外的检测电路或者较为复杂的运算方法来提取较大幅值的基波电流中占比很小的直流分量；智能算法是一种采用高级算法进行直流分量提取和抑制的策略，具有鲁棒性强的特点，但需要消耗较多的计算资源，实时性也有待提高。电容隔直法是一种利用电容“隔直通交”固有特性的策略，根据隔直电容的位置，可以分为直流侧和交流侧两种。半桥类拓扑是典型的直流侧含隔直电容的结构，具有内在的直流成分抑制能力，但也存在电容电压不平衡和直流电压利用率较低等不足[5]；而将隔直电容置于交流侧时，如图1a 所示，该方法简单直观，但也存在容值选取困难[6]、电容的串联电阻降低逆变器效率等不足。

为此，GUO 等[7]提出了虚拟电容的思路，如图1b 所示，在控制器中引入基于进网电流积分运算的前馈项来等价实现交侧串联电容的直流分量抑制效果。然而虚拟电容法也存在自身的问题，比如：影响原本电流控制器的稳定性和动态性能等。因此，应用虚拟电容法时往往要对电流控制器参数和虚拟电容的容值进行合理整定，才能满足直流成分抑制速度快并且基波电流响应又快又准的要求。文献[7]在对比了不同容值下系统的单位阶跃响应后，定性地给出了选取的容值，但没有具体分析虚拟电容对基波电流响应的影响；文献[8]借助根轨迹和伯德图等频域分析工具，综合分析了虚拟电容与比例协助(Proportional resonant，PR)电流控制的相互影响，但最终参数的选取仍是由仿真尝试后给出的经验取值，并不能形成一般的指导原则。文献[9-10]将虚拟电容的概念应用于三相并网逆变器系统，使用根轨迹法分析了比例积分谐振(Proportional integral resonant，PIR)控制器的参数选择。但论文中认为工程上对直流分量抑制的动态性能要求不高，因此直接选取了较大的虚拟电容容值，处理方式过于简单。以上文献在选取虚拟电容的容值和电流控制器参数时，均未对系统的时域指标进行约束；而文献[11]从稳态误差、开环系统基波幅值增益、幅值裕度和相位裕度角度对控制器参数设计提出了具体要求，并通过拟合约束条件曲线得到了参数选择的允许域，但步骤过于繁琐。

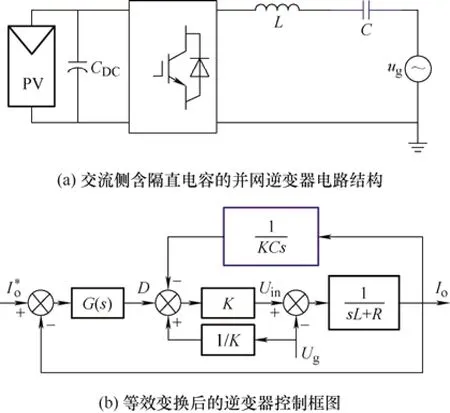
图1 交流侧含隔直电容的并网逆变器电路结构及其等效的控制框图

为了对电流控制器参数和虚拟电容的容值进行合理的整定，本文提出一种比例谐振控制器和虚拟电容(Proportional resonant controller and virtual capacitor，PR+C)控制参数优化方法，旨在兼顾直流成分抑制速度和基波电流跟踪效果。提出的评价指标计算简单易行，可以指导逆变器实际调试时控制器参数整定工作。

2 带虚拟电容的并网逆变器控制系统

当PR 控制器应用于进网基波电流控制时，式(1)中的ω应取100π，而比例系数kp和kr则需要进一步调节以达到期望的控制效果。

根据图1b 和式(1)可以得到逆变器系统的输入输出关系，如式(2)所示。由于电网电压前馈的作用，电网电压对系统的影响可以基本忽略[12-14]，从整体来看控制系统变为单输入单输出系统。

作为对比，将图1b 中的虚拟电容移除，得到输入输出闭环传递函数如式(3)所示

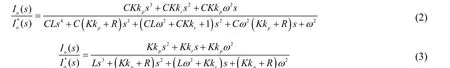
3 虚拟电容与PR 控制相互影响分析

为了阐明虚拟电容与PR 电流控制的相互影响，需要借助时域响应和频域响应曲线做进一步分析。首先要确定除C及kp、kr以外的参数，选定的逆变器基本参数如表2 所示。

表2 用于分析的逆变器基本参数

3.1 虚拟电容对直流成分抑制能力分析

在式(2)中，令s=jω=0，则有Io(jω)=0。即理论上，虚拟电容抑制直流分量的稳态误差为0。但不同的容值选取，会产生不同的直流成分抑制速度和不同的响应形式。

当PR 控制器参数kp=0.05、kr=10 时，以不同的虚拟电容容值，绘制逆变器系统的单位阶跃响应曲线进行对比，如图2 所示。在0 时刻输入单位阶跃信号，即参考电流由0 A 突变为1 A。

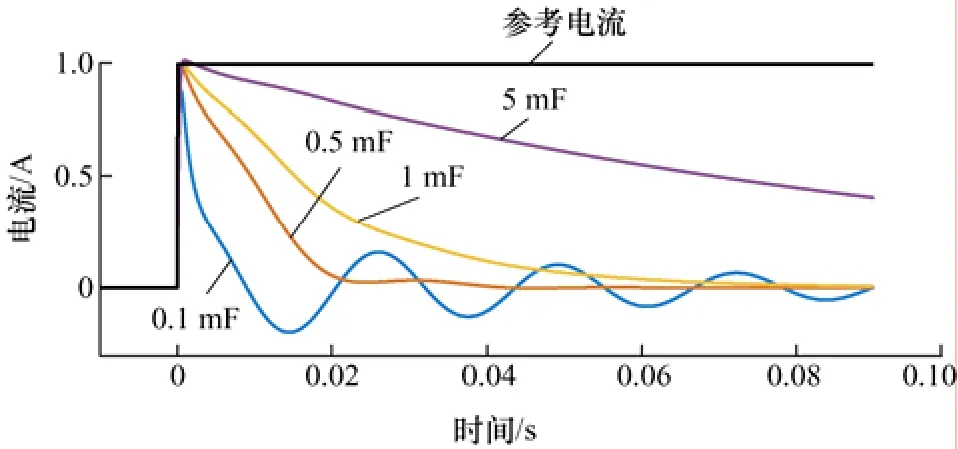
图2 虚拟电容容值不同时系统的阶跃响应

观察四种容值下的阶跃响应可以得出如下结论。

(1) 虚拟电容容值过大会导致直流抑制的动态响应变慢。

(2) 虚拟电容容值过小会导致系统输出产生振荡。

(3) 虚拟电容容值大小不影响系统阶跃响应的稳态值(时间趋于无穷)。

上述结论可以通过绘制系统闭环传递函数的频响曲线进行验证。图3 包含了虚拟电容容值C分别取0.1 mF、0.5 mF、1 mF、5 mF 的频响曲线，此外也包含了无虚拟电容时系统的频响曲线。从图3 可以看出，不设虚拟电容时，系统在低频(趋近于0)的增益为1，而当C从5 mF 减小到0.1 mF 时，系统对低频成分的衰减逐渐增大。同时也可以发现，在50 Hz 附近，电容越小，系统的幅值增益越大，因此当输入信号包含50 Hz 左右的成分时容易引起振荡。

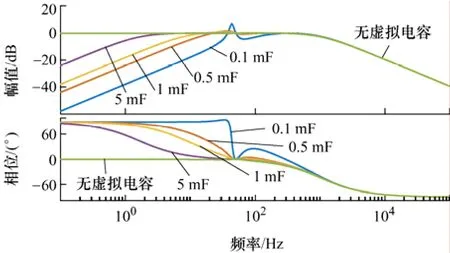
图3 虚拟电容容值不同时系统的频响曲线

综上所述，为了实现直流成分抑制速度快且振荡小的目标，虚拟电容的容值在选取时应存在一定的约束条件，下文中将给出具体指标。

3.2 虚拟电容对基波电流控制能力的影响分析

为了分析虚拟电容对PR 控制器动态跟踪能力的影响，图4 对比了进网电流参考突变时不同容值下的电流响应曲线。其中参考电流的幅值在0.265 s时由10 A 突变为5 A，PR 控制器参数kp仍取0.05、kr仍取10，而C分别取0.1 mF、0.5 mF、1 mF、5 mF。

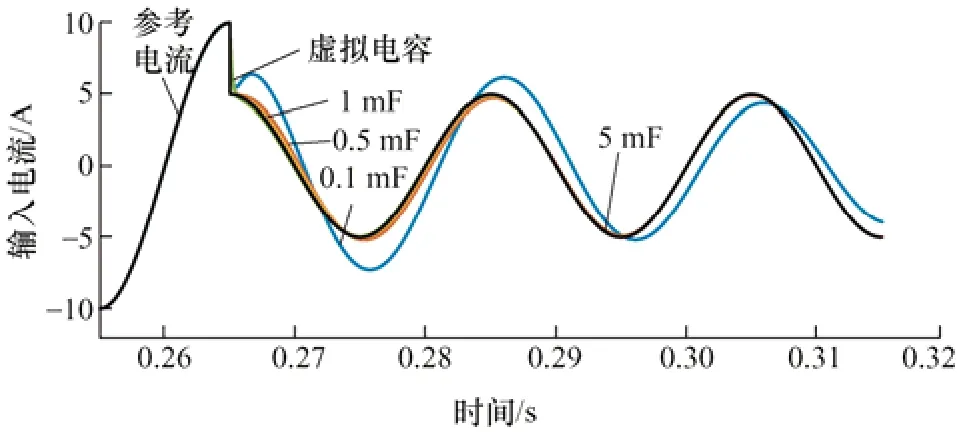
图4 不同容值下系统对基波输入电流的动态响应

3.3 PR 控制器对直流成分抑制能力的影响分析

为了说明PR 控制器参数对虚拟电容抑制直流的影响，下面对比不同的控制器参数下逆变器系统的单位阶跃响应。当虚拟电容容值C=1 mF、PR 控制器参数kr=10 时，将kp分别取为0、0.01、0.03和0.05 绘制系统的单位阶跃响应曲线，如图5 所示。此外，图6 对比了当虚拟电容容值C=1 mF、PR 控制器参数kp=0.05 时，kr分别取0、3、6 和10 下，逆变器系统的单位阶跃响应曲线。

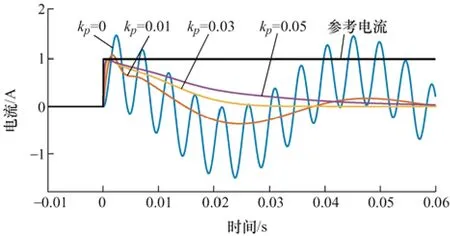
图5 比例参数kp 不同时系统的阶跃响应

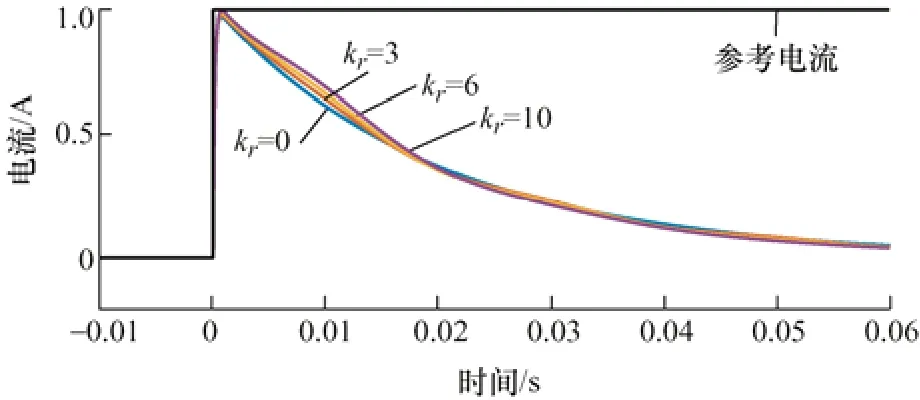
图6 谐振参数kr 不同时系统的阶跃响应

结合图5、6 可知，比例参数kp会显著影响系统的阶跃响应形式。当kp逐渐增大，阶跃响应的振荡逐渐消除的同时，直流成分的抑制速度也会逐渐放缓。而相较而言，谐振参数kr并不会对虚拟电容抑制进网电流成分的效果造成严重的干扰。上述两点结论同样可以通过系统的频响曲线进行验证，在此不再赘述。

综上，虚拟电容与PR 控制器相互耦合，共同影响着逆变器系统的基波电流跟踪性能和直流成分抑制能力。因此，有必要对参数选择的结果进行指标上的量化和约束，以达到期望的逆变器性能。

4 控制参数最优方法与实践

4.1 约束条件建立

4.1.1 频域指标

逆变器系统的幅值裕度和相位裕度应满足以下条件。

(1) 开环系统的相位裕度在30°～90°。(2) 开环系统的幅值裕度在6～8 dB[15-17]。

使用以上两个条件可以在参数空间求出一个区域，以便下文进行最优解的选择。由图1b 可求得控制系统的开环传递函数

由于系统使用了PR 控制器，因此幅值裕度为无穷大，自动满足幅值裕度约束。在已知逆变器系统的其他基本参数后可得频域指标，即kp、kr、C满足

很多人认为社保征收体制改革将会给企业带来致命性的打击，企业将无法承担由此带来的成本的增加，从而引发企业的倒闭潮，面临舆论的压力，国务院也于近日做出表态，保证社保征收体制改革以后总体上不会增加企业的负担。笔者认为：如果未来继续降低企业社保社保费率，而公务员的薪酬制度不做相应改变，这将可能进一步拉大公务员和企业人员收入差距，激化社会矛盾。

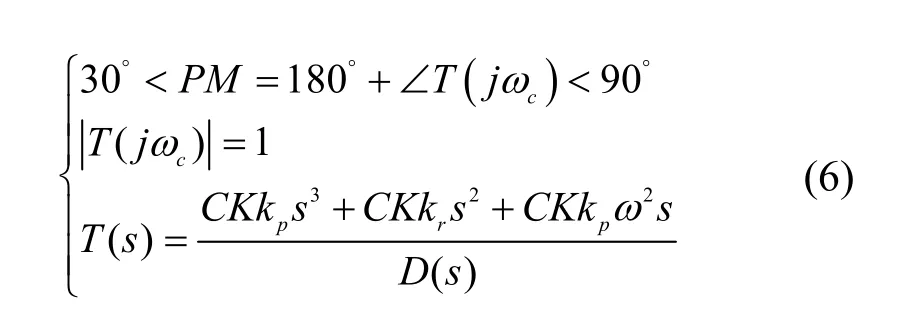
式中，PM代表相位裕度；等式|T(jωc)|=1 的解ωc为最大的开环截止频率。因此根据式(6)可以确定一个关于kp、kr、C的参数选择区域。

4.1.2 时域指标

频域约束并不能直接决定系统时域特征的优劣，本节将对系统具体的时域响应给出评价指标。这些指标从两个需求出发：直流成分的抑制效果和进网基波电流的跟踪效果。

根据前文分析，由于选择的控制参数不同，单位阶跃响应的形式可以按照是否出现负响应波形分为两类，即振荡衰减的响应形式和非振荡的响应形式。无论哪种形式均能达到期望的响应性能，本文重点讨论振荡衰减的类型。

当系统的单位阶跃响应出现正负振荡形式时，采用如下指标。

(1) 在阶跃响应中，令

式中，n代表一种衰减比，hmax、hmin分别是系统的单位阶跃响应最大、最小时的数值。当n越小时，说明振荡幅值衰减大，直流成分抑制效果越好。

(2) 在阶跃响应中，求解tnp时刻满足

式中，H(t)代表阶跃响应。当求解出的tnp越小时，说明振荡收敛越快，直流成分抑制效果越好。

(3) 在给定输入信号R(t)的响应中，令

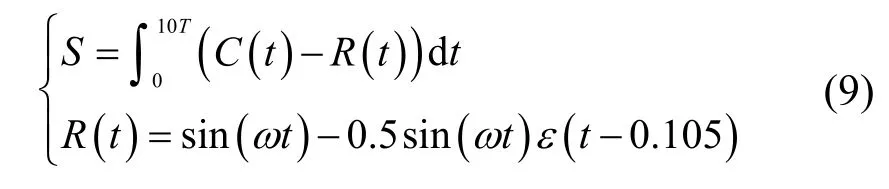
式中，积分数值S代表逆变器系统输入与输出之间的差值，C(t)为系统响应，ε(t- 0.105)为延时至0.105时刻的单位阶跃函数。因此当S越小时，说明基波电流跟踪越误差越小，PR 控制效果越好。

综上三点，得到评价逆变器系统交直流控制性能的目标函数

式中，α、β、γ分别为三种指标的权重，调节三者的大小可以满足不同的筛选偏好。

最后，将满足频域指标的参数组代入式(10)，找到使得目标函数最小的参数组，即找到了定义的最优参数组(kp、kr、C)。

4.2 参数优化求解

本节以表2 所列单相并网逆变器参数为例，进行控制参数优化的求解。

首先求解满足频域指标的参数组，即采用有限离散化数值运算的方式，求出控制参数不同时的系统相位裕度。考虑到计算机算力，此处kp离散化的分度取为0.001、取值范围为(0, 0.05]；kr离散化的分度为1、取值范围为(0, 20]；C离散化的分度为0.000 1、取值范围为(0, 5×10-3]。

相位裕度计算结果如图7 所示，该三维坐标系中的每一点都对应一个参数组(kp、kr、C)。图7 中左侧点的相位裕度小于30°，使用了空心圆圈进行标记；右侧区域为满足相位裕度(大于30°)的点，此处使用实线灰度的深浅表示不同参数下系统的相位裕度大小。

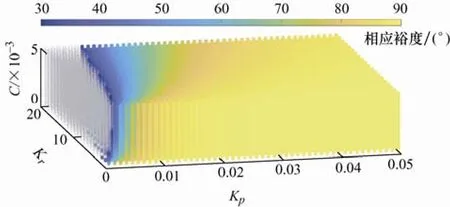
图7 相位裕度满足30°～90°的kp、kr、C 参数组

接着求解目标函数最小的参数组。由于不同待定参数下的约束指标数值相差很大，甚至不在一个数量级，因此需要对各组控制参数下的同一指标值进行归一化。例如

式(11)表示将每一组kp、kr、C下，求出的指标数值A，除以所有kp、kr、C取值下最大A与最小A的差值，把原本的数据归一化到区间[0, 1]上。以此类推，对所有的指标都进行上述归一化后，再对各个指标进行加权以计算目标函数值。

令α=1、β=1、γ=10，并筛选图7 中满足阶跃响应为衰减振荡形式的参数组，代入式(10)计算目标函数数值。此处同样以实线灰度的深浅区分数值大小，计算结果如图8 所示。

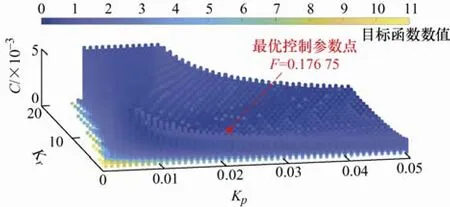
图8 阶跃响应有振荡时各参数组目标函数的数值

最终，将各参数组下的目标函数值从小到大排列，得到F有最小值0.176 75，如图8 所示。此时最优控制参数组为kp=0.024、kr=7、C=0.001 1。

5 仿真与试验验证

为了验证由传递函数数值计算得到的最优控制参数的正确性，本节进行在实际物理模型下的Simulink 仿真，逆变器硬件参数如表2 所示，控制参数kp=0.024、kr=7、C=0.001 1。给系统输入特定的参考电流波形，具体如下：参考电流从0 时刻到0.045 s 幅值均为5 A，0.045 s 后幅值突变为10 A；在0.08 s 时加入了2 A 的直流分量。

其次，为了对比虚拟电容与实际电容的差别，另于逆变器网侧串联1.1 mF 的电容进行仿真，导出输出电流并与使用虚拟电容时进行对比，仿真结果统一绘制在图9 中。

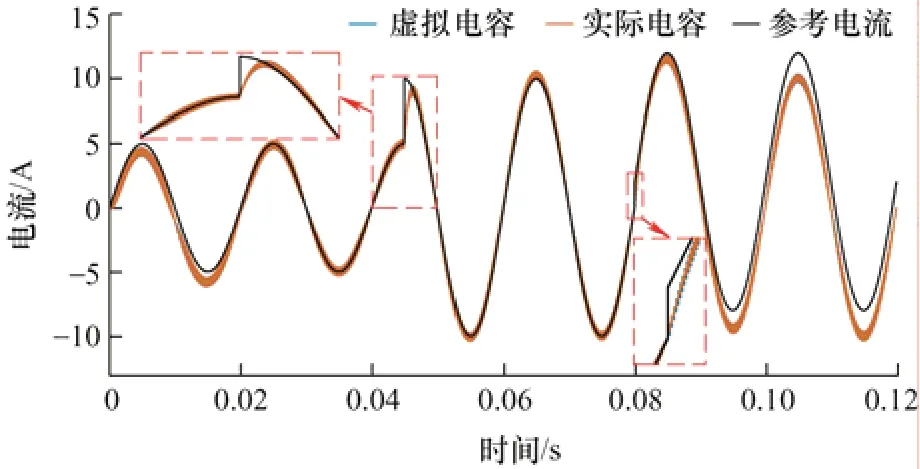
图9 系统电流跟踪和直流抑制在实际电容与虚拟电容下的对比

图10 为试验样机逆变器先经历软启动过程后电流保持在10 A 幅值运行，接着在正峰值处参考电流幅值突变为5 A，最后在由负向正过零点处给参考电流叠加 1 A 的直流分量，即参考电流为5sin(ωt)+1 工作情况下的波形图。

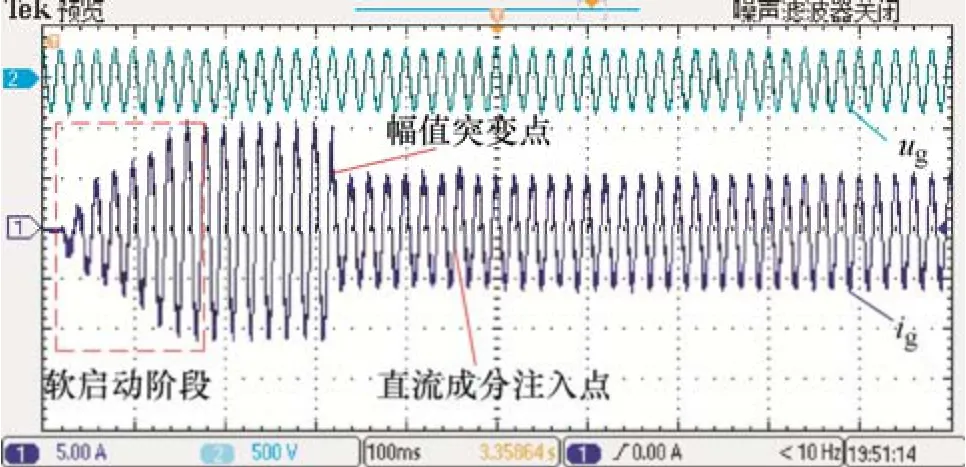
图10 进网电流动态响应过程波形

从仿真和试验波形可以看出，启动时输出电流能跟踪上参考电流，参考电流幅值突变时输出电流能够迅速反应；最后当参考电流引入了直流成分后，输出电流也能够在约一个电网周期后消除直流偏移。初步验证了参数选择的正确性。

此外，使用实际电容与虚拟电容抑制进网电流直流成分的结果基本重合，证实了虚拟电容法替代串联在电路中的实际电容切实可行，进一步验证了参数选择的正确性。

6 结论

虚拟电容与电流控制器相互耦合，共同影响着逆变器系统的基波电流跟踪性能和直流成分抑制能力。因此，使用虚拟电容法需要建立在合理选择虚拟电容容值和电流控制器控制参数的基础上。本文提出的一种PR+C 控制器参数优化方法，可使用数值计算的方式得出最优参数组，旨在为逆变器的控制器参数整定提供指导。通过调节目标函数的权重，可按需平衡并网逆变器进网直流抑制速度和基波电流跟踪效果。仿真结果表明方法切实有效。当然，该方法也存在自身的问题，例如：参数选择需要进行大量的数值运算、最优参数的选择仍然是建立在参数选择空间的遍历上而不能实现直接求解最终结果等，这都需要后续的工作进行改进。