基于等强度设计的制动器结构件轻量化探索*

潘全章，赵春光

（1 北京纵横机电科技有限公司， 北京 100094；2 中国铁道科学研究院集团有限公司 机车车辆研究所， 北京 100081）

1 多目标拓扑优化

随着产品的迭代周期缩短，基于参数化设计的方法在解决结构件轻量化问题上耗时长、效率低的特点影响了产品更新速度。需要利用拓扑优化的方法，根据负载、空间的约束，在给定区域内对材料分布进行优化。

交通领域是轻量化设计的典型应用领域，因此与可类比的实体设计相比较轻量化设计必须是安全的［1］。对于制动单元的拓扑优化，需要同时考虑到结构强度和刚度，并且在静载和振动载荷条件等多工况下进行，属于多目标拓扑优化。

结构多目标拓扑优化技术是将多目标优化技术应用于结构优化领域，是近年来各领域都在争先研究的领域。该问题中要求静态多刚度拓扑优化中的柔度目标不高于优化前水平，同时模态拓扑优化中的平均固有频率不低于优化前水平，因此须对多个目标函数进行处理才能实现对制动单元结构件的多目标拓扑优化。文中使用折衷规划法将多个目标函数整合为一个目标函数，并根据经验对各个目标函数添加权值，使用的公式为式（1）［2］：

式中：Ck（x）为静态刚度工况下的目标函数值；Cmink为第k个工况下的最小柔度；Cmaxk为第k个工况下的最大柔度值；Λmax为制动器上待优化零件的最大平均固有频率；Λmin为改进前的最小平均固有频率；Λ(λ)为模态拓扑优化中的目标函数。

2 点阵结构设计方法

随着高新技术的发展，人们已经不再满足于材料单纯的轻质化，而是寻找兼有轻质和其他某种或某几种优良性能相结合的先进材料以适应不同的需求［3］。点阵结构如图1 所示，也被称作微型桁架结构（Lattice or Truss），在2000 年左右由美国多个大学教授联合提出，该结构借鉴金属原子结构体心立方、面心立方等排布形式，形成了三角形、四面体、八面体、Kagome 等多种胞元形式如图2 所示。不同胞元形式会对结构宏观力学性能产生不同的影响［4］。

图1 点阵结构

图2 点阵结构胞元形式

点阵结构具有很高的比强度、比刚度，因此可以有效减少结构件质量，并且可以通过材料综合密度、胞元形式的优化组合，定制结构件力学性能。

随着制造水平的提升，点阵结构已经在航天、汽车、医疗等领域得以应用。近年来，相应制造工艺成本下降，为其在轨道交通行业的应用提供了可能。

点阵材料弹性模量计算为式（2）：

式中：C是一个常数，与胞元结构有关，对于三角形胞元C=1.15；Es为材料本身的杨氏模量；t为点阵结构胞元各边的厚度；l为胞元边长。

3 制动杠杆设计案例

以制动杠杆为例，运用上述方法，开展等强度结构优化设计如图3 所示。

3.1 有限元模型信息

材料：钢，对应参数为弹性模量210 GPa；泊松比0.3；材料密度7 850 kg/m³；模型质量7.73 kg。

约束条件：中间位置组孔5 自由度约束，可转动；右侧位置组孔6 自由度约束。

载荷条件：在左侧组孔位置施加纵向40 000 N的力载荷。

计算结果为：最大应力值237.5 MPa，加载点综合位移为0.61 mm。计算结果的应力云图、位移云图如图4、图5 所示。

图4 初始设计应力云图

图5 初始设计位移云图

3.2 优化及分析

首先根据提供的边界条件及力学环境条件，对该支架进行优化设计。仍然选取钢作为优化后材料。

优化变量：除加载孔以外材料为拓扑优化的设计空间，如图6 所示。

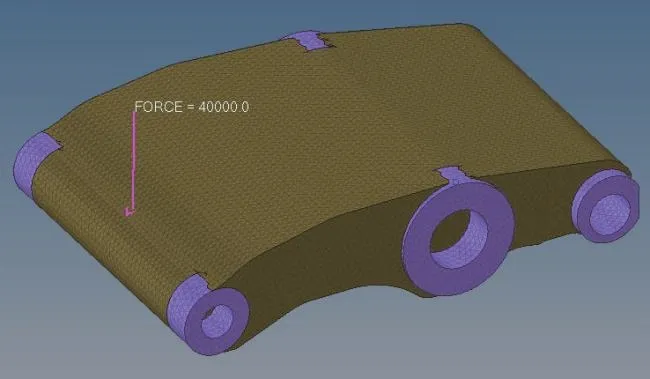
图6 优化空间

约束函数：应力小于235 MPa，加载点综合位移不大于0.65 mm。

目标函数：质量最小化。

优化计算结果如图7 所示。

图7 优化计算结果

3.3 拓扑优化方案及校核

根据优化后的结果，进行模型重建。重建的模型如图8 所示。

图8 几何重建后模型示意图

优化模型进行校核计算，优化计算结果的应力云图、位移云图如图9、图10 所示。

图9 拓扑优化方案应力云图

图10 拓扑优化方案位移云图

优化后模型质量5.4 kg；优化后的结构应力分布基本为等应力分布，应力最大值为225 MPa；加载点综合位移为0.65 mm，与优化前相比满足优化要求。

3.4 点阵结构方案及校核

根据设计空间，蒙皮采用shell 单元计算，内部点阵采用等效实体单元计算。设计模型如图11 所示，材料分布优化模型如图12 所示。

图11 设计模型

图12 优化模型

优化模型进行校核计算，优化计算结果的应力云图、位移云图如图13、图14 所示。

图13 三维点阵结构应力云图

图14 三维点阵结构位移云图

优化后模型质量3.7 kg；优化后的结构应力分布基本为等应力分布，应力最大值为210 MPa；加载点综合位移为0.65 mm，满足优化要求。

4 小 结

根据前期优化及设计、校核结果，目前设计指标对比见表1。

表1 优化前后设计指标对比

由上可知，通过等强度设计理念，可以利用拓扑优化及点阵结构更大限度地发挥所有材料的承载能力，从而有效降低结构件设计质量。

下一步，将会探索上述方案的工程实现方法，并对样机进行试验验证。