基于熵值-TOPSIS模型的区域物流发展能力研究

(福建农林大学交通与土木工程学院，福建 福州 350002)

伴随着我国社会经济的飞速发展，物流业也飞速发展。物流业作为我国国民经济发展的基础性产业，对于区域经济的发展具有举足轻重的作用。因此，研究区域物流发展能力，并比较其发展水平具有十分重要的现实意义[1-4]。在区域物流方面，前人已做了大量的研究，其中较为传统的是使用熵值法和层次分析法，结合实例进行求解，得出较为理想的结果[5]。也有学者运用R聚类法从众多指标中筛选出最优指标，并结合熵值法构建评级指标体系，通过使用模糊物元评价法对该研究地区进行综合评价[6-7]。不仅如此，在评价方案指标上，前人结合AHP法与TOPSIS法，建立AHP-TOPSIS的综合评价指标体系，以此建立模型并分析何种方法效果最优[8]。通过结合主观评价法和客观赋权法，创建多指标综合赋权评价体系，最后结合实例分析其可行有效性[9-11]。本文结合物流业与经济发展等因素，分析其发展关系，确定区域评价指标体系，使用熵权法确定其指标权重，并使用TPOSIS评价，分析区域物流业发展现状，评价区域物流发展能力[12-16]。

1 熵值法确定权重

在确定数据权重中，熵值法具有客观赋权性，可根据其指标所代表的数据确定指标权重。在熵值法中，设存在m与n个评价方案与指标，构建评价矩阵M=(Xij)mn，通过求解的离散程度确定该指标对评价对象的影响程度，从而可计算出各个指标的权重[17-18]。

1.1 贡献度的确定

选取指标，构建评价矩阵

(1)

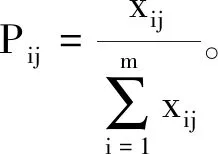
(2)

1.2 贡献总量的确定

属性值由所有方案差异大小来决定权系数的大小，可定义各方案贡献度的一致性。

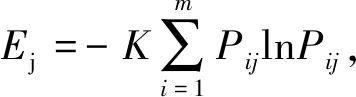
(3)

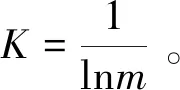
(4)

其中，Ej表示方案中Xj的贡献总量，m为方案数。

1.3 属性权重的确定

直接利用决策矩阵所给出的信息计算权重

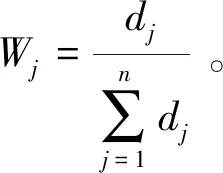
(5)

若已计算出主观估计权重，则可采用上述Wj对λj进行修正，如下所示

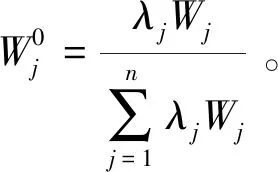
(6)

2 熵值-TOPSIS模型综合评判法

对多指标数据进行综合评价可选择逼近理想排序法，通过对评价研究对象的分析，对其与最优劣解间的距离进行分析。通常，接近最优解为最好，反之接近最差解为最差。本次模型建立不参杂任何主观因素，以此确保数据分析的客观证实可信度[19-22]。

2.1 归一化处理

对评价对象矩阵进行归一化数据处理，求标准化矩阵uij。正向指标归一化，

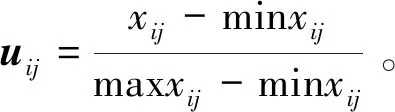
(7)

负向指标归一化，

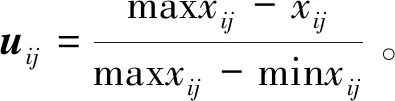
(8)

2.2 建立加权标准化矩阵

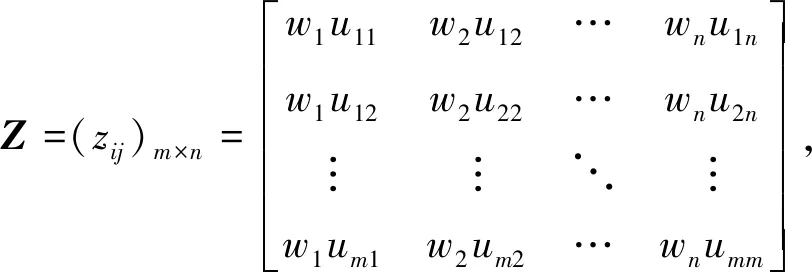
(9)

其中，Zij为熵权法确定的各个指标体系权重wn与归一化矩阵uij的每列相成所得。

2.3 确定正负理想解

理想解

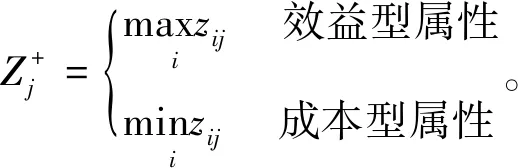
(10)

负理想解

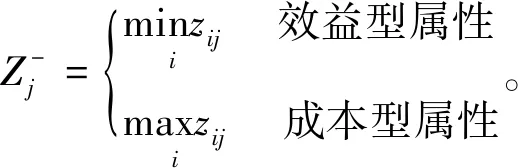
(11)

确定各研究对象到正负理想解之间的距离。到理想解之间的距离

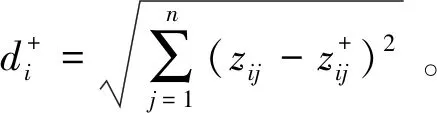
(12)

到负理想解之间的距离

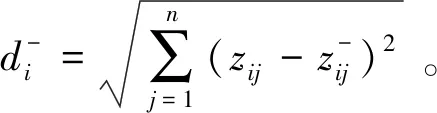
(13)

2.4 评判对象与理想解的接近程度

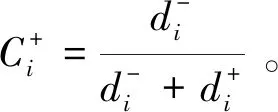
(14)

2.5 综合评判向量

(15)

将各个评判对象的优劣次序按由小到大对F进行排序。

3 实例分析

根据区域物流发展不平衡现状及区域经济水平[23]，对目前区域物流运输发展现状进行评价分析。在此基础上可得出区域物流发展较好的模式，与其他邻边区域协同发展，促进经济进步，加快物流发展。本次以福州，厦门、泉州和莆田4个邻近区域作为评价主体，根据传统评价指标体系以及区域特性构建区域物流评价指标体系(图1)。

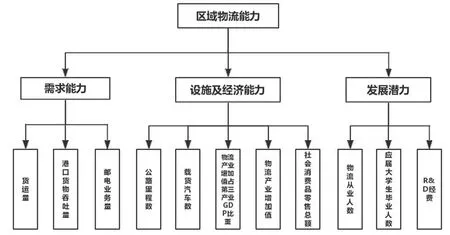
图1 区域物流评价指标体系Fig.1 Regional logistics evaluation index system

3.1 区域数据指标确定

经过比较分析近五年的城市统计年鉴，福州、厦门、泉州和莆田各评价指标均呈现稳步增长，因此，本次研究选取数据来自《福建统计年鉴-2019》[24]中2018年度数据(表1)。

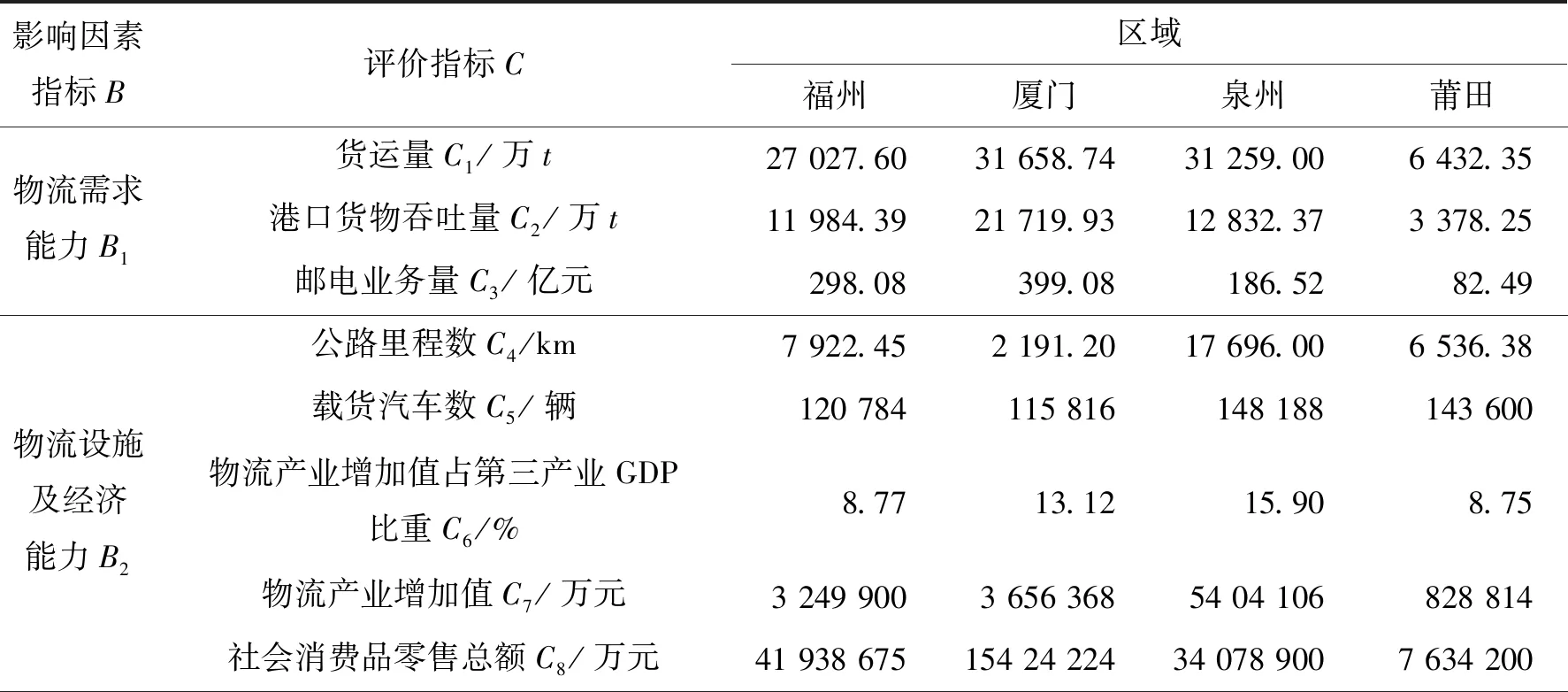
表1 2018年区域物流能力评价指标数据

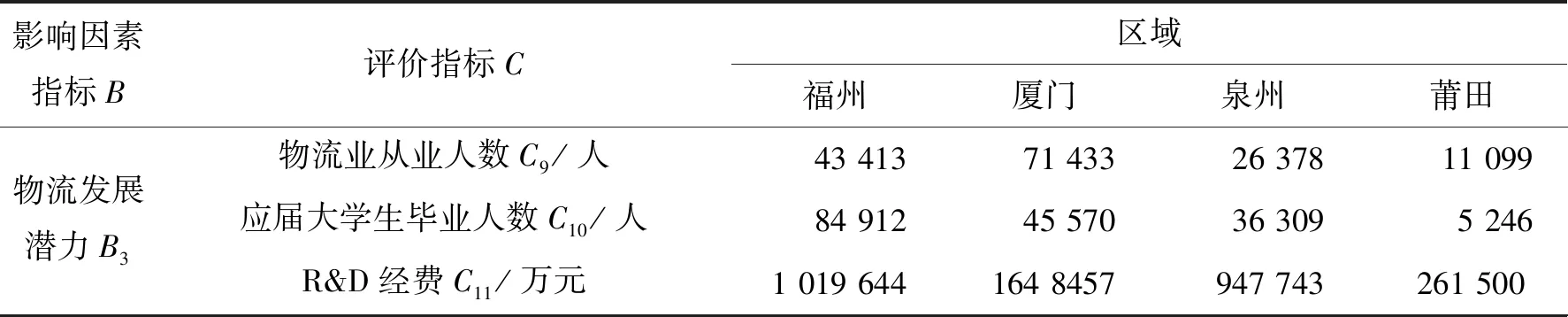
续表

本次选取的指标应为本区域物流发展的代表性指标，并能最大程度反应物流发展现状。物流发展模式的评价为一个整体工作，牵扯面广，因此有必要对其进行整体分析。在评价体系中，准则层选取物流需求能力、物流设施及经济能力和物流发展潜力3个指标。其中，物流需求能力由货运量，港口货物吞吐量和邮电业务量构成；设施及经济能力由公路里程数，载货汽车数，物流产业增加值，物流产业增加值占第三产业GDP比重和社会消费品零售总额构成；物流从业人员，应届大学生毕业人数和R&D经费构成了物流发展潜力。在此基础上，从2018 年统计年鉴中选取其指标所对应的数据。

3.2 熵值法指标权重确定

借鉴了熵值法，在此基础上确定福州、厦门、泉州和莆田4个城市所选取数据指标的权重。

1)根据式(1)～式(2)，求得第j个属性下第i个方案Ai的贡献度，如表2所示。

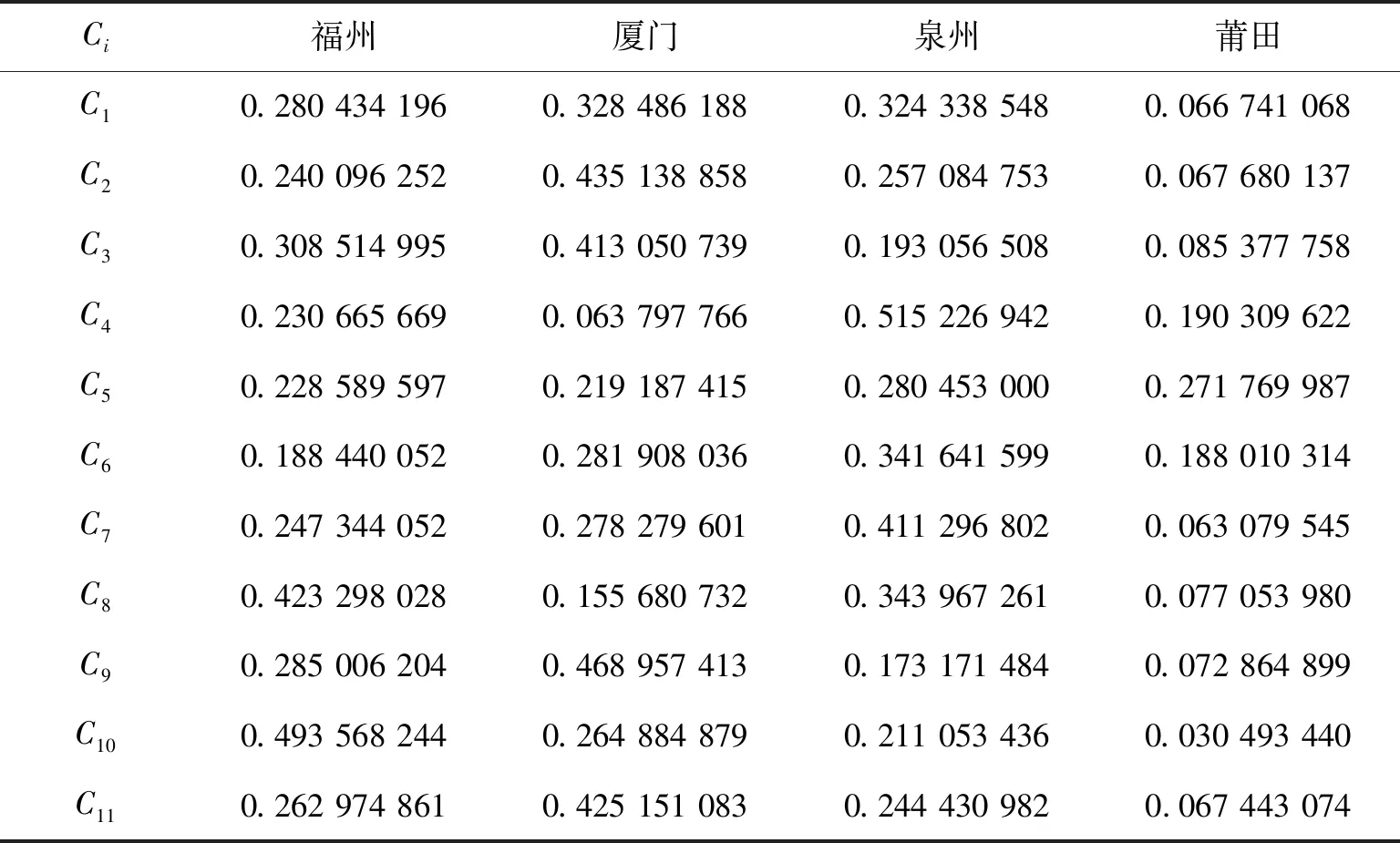
表2 各数据指标贡献度

2)根据式(3)求出Xi的贡献总量，数据处理如表3所示。

3)根据式(4)～式(6)求出常数k，k为1/ln(方案数)，并求Wj,结果如表4所示

k=1/ln(4)=0.721 34。

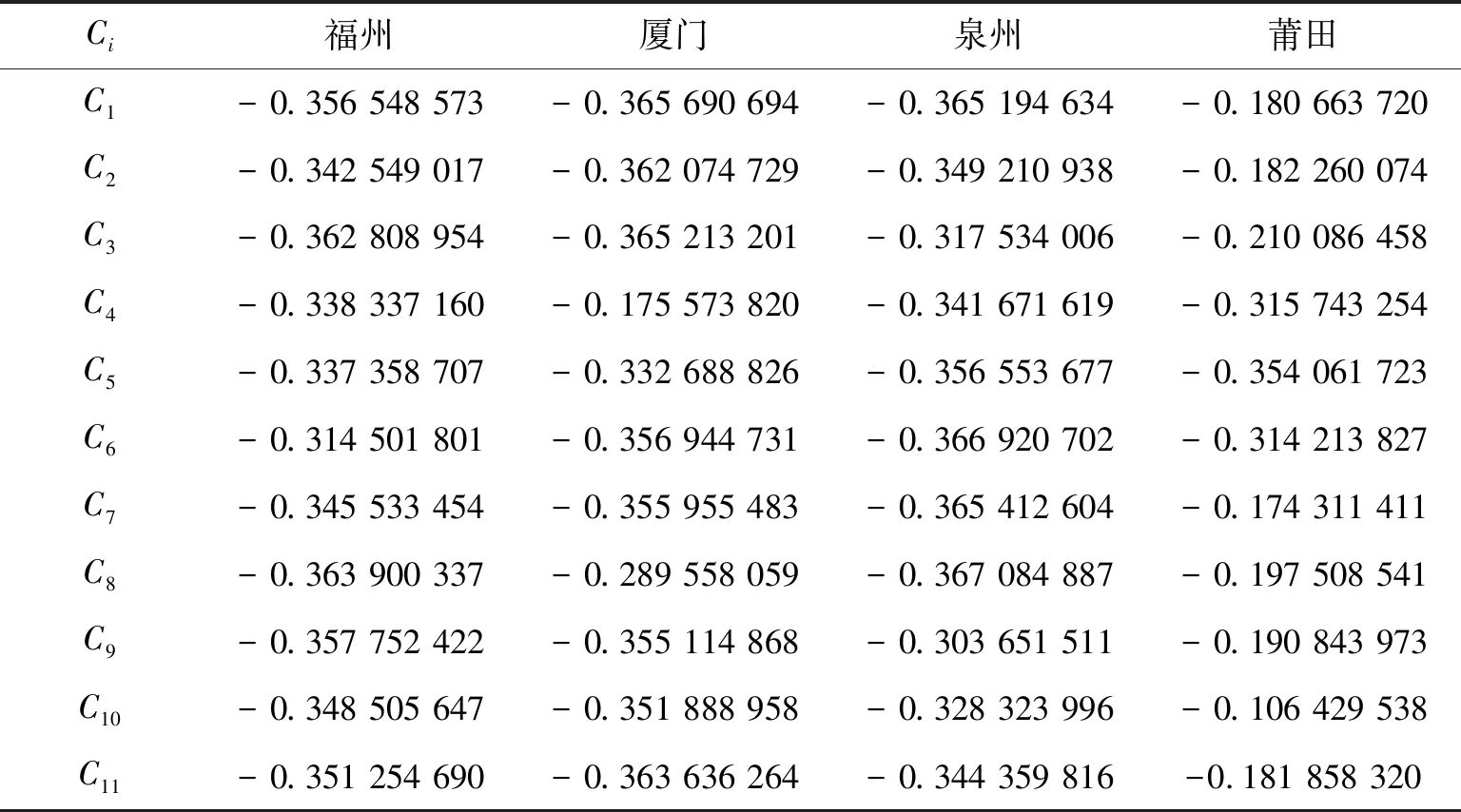
表3 各数据指标贡献总量

表4 各指标相对权重

3.3 TOPSIS法综合指标评判

3.3.1 物流需求能力分析

根据式(7)～式(9)，构建评判矩阵与加权规范矩阵。

根据式(10)～式(11)，在此需求指标中，物流货运量、港口货物吞吐量和邮电业务量均属于效益型属性，基于此，正负理想解如表5所示。

表5 需求指标正负理想解

根据式(12)～式(13)式确定各指标到正负理想解之间的距离。

表6 需求指标到正负理想解距离

通过与理想解的贴近度分析可知，在物流需求能力评判指标中，厦门的物流需求能力最强，最差为莆田。由于厦门在物流需求能力指标中全为最大，莆田在物流需求能力中全为最小，且评价指标均为效益性指标，因此出现了厦门与理想解的贴近度为“1”，而莆田与理想解的贴近度为“0”的结果。

3.3.2 物流设施及经济能力分析

如上物流需求能力分析，同理可得，物流设施及经济能力中各指标到正负理想解之间的距离如表7所示。

表7 设施及经济指标到正负理想解距离

通过与理想解的贴近度分析可知，在物流设施及经济能力评判指标中，泉州的物流设施及经济能力最强，说明泉州作为福建经济实力最强的城市，在物流行业发展方面也比较强。

3.3.3 物流发展潜力能力分析

各指标到正负理想解之间的距离如表8所示。

通过与理想解的贴近度分析可知，在物流发展潜力能力评判指标体系中，福州物流发展趋势最好，厦门物流发展潜力能力仅次于福州。

表8 发展潜力指标到正负理想解距离

3.4 熵值法-TOPSIS法综合评判

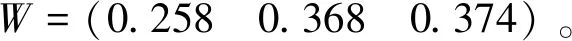
根据式(14)～ 式(15)计算得各区域指标与理想解的贴近度矩阵为

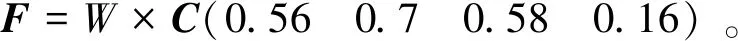
根据以上综合各项指标因素分析，物流总体能力从大到小依次为厦门、泉州、福州、莆田。泉州在物流设施及经济能力这一指标上得分最高，福州在物流发展潜力能力评判指标上领先，而莆田各项指标均较弱。

3.5 物流能力差异分析

本次研究在构建指标的基础上，通过对其物流需求能力，物流设备和物流发展潜力3个方面进行了数据分析，从结果中可以看出4城市间物流能力发展现状。在分析中发现，在物流需求能力上，厦门在货运量、港口货物吞吐量、邮电业务量3个方面在4个城市中呈领先地位，分析显示厦门物流需求能力与理想解的贴近度为1，发展模式相对较好。在物流设施及经济能力上，泉州的分析结果与理想解的贴近度为0.64，得益于物流产业增加值和物流产业占第三产业GDP比重相对较高，说明泉州较重视物流业的发展，使其在物流设施及经济能力相对于其他城市较为突出。在物流发展潜力能力，福州与厦门相对泉州和莆田较高，应届大学生人数和R&D经费为这两个城市提供了充足并且稳定的发展潜力，这对于今后物流业的发展具有重要意义。通过分析探讨，厦门、泉州和福州分别在物流需求能力，物流设施及经济能力和物流发展潜力上各自达到领先地位。通过综合评判，厦门物流总体能力分析结果与理想解的贴近度为0.7，达到4个城市的最大值。同为沿海城市，莆田的物流发展能力相对较差，这可能由于其交通基础设施建设相对较少、物流人才较少、资源投入不够等原因。

4 结论与建议

本文将区域物流业的发展与区域经济发展等因素相结合，构建了区域物流能力评价指标体系。研究结果表明，区域物流能力发展不均衡，其中厦门市物流能力最强，与莆田市差距较大，主要是由于物流需求能力、物流设施及经济能力、物流发展潜力等方面差距明显造成的。因此，对福州、厦门、泉州和莆田区域物流业发展提出以下建议：

1)提高物流发展需求，加强区域经济发展。从研究结果中发现，厦门、泉州经济能力较强的城市其物流能力也往往比较高。经济能力较弱的城市可依靠经济较强的城市发展，以经济发展为中心，提高经济能力，增强物流发展能力。

2)加强物流业基础设施建设，促进区域物流业发展。泉州的物流基础设施使其在物流能力评价中处于较为靠前的位置。因此，经济能力较弱的区域应更加注重物流基础设施对物流能力的促进作用，可加强对路网等物流基础设施的建设，提高区域物流业的输送效率。

3)加强物流业科技创新，提升区域物流创新能力。随着物流业发展的智能化，对现代物流业的发展提出了更高的要求。因此，各区域可通过培养物流专业人才以及人才引进方式，提高物流从业人员的专业能力，提高区域物流能力。

4)加强区域合作，构建区域物流发展体系。区域物流一体化发展有利于城市间共享有利资源，优势互补，加快物流服务产业升级，形成物流产业圈，提高区域供应链的竞争力。