基于PSO-RBF算法的冷凝器运行特性分析

耿洪健，姜 伟

(海军工程大学舰船综合试验训练基地，湖北 武汉 430033)

1 引言

冷凝器负荷动态过程是维持舰艇动力装置的安全稳定运行的重要因素[1]。对于冷凝器动态特性的数学建模问题，根据应用场合标准和要求的不同主要可以分为两类：第一类是机理建模，如为分析冷凝器内各个相区长度随时间的变化，北京航空航天大学的王武超等提出了采用移动边界法建立冷凝器动态仿真数学模型，从而兼顾了仿真的效率和精度[2]。上海理工大学的汪敏等建立了平行流式冷凝器的计算模型，并分别对不同风速、环境温度、质量流量下的传热和流动特性进行了模拟计算[3]。在实际研究中，机理分析总是基于很多简化和假设之上，这就使得机理建模与实际过程之间有一定的误差，特别是随着舰艇服役时间的增加，运行状态必然会发生改变，此时机理模型不能跟实际设备有一致的响应，难以满足实时计算的要求。

另一类是直接采用试验结果进行数据拟合的方法进行建模研究，该类方法又称为辨识建模，是指通过将一系列测试信号(试验数据)输入实际过程，测试其响应，从而建立过程模型，被称为“黑箱”建模，如重庆大学的黄光勤等通过拟合的方式得到了热泵机组蒸发器、冷凝器的水温和水量修正系数的多项式函数，从而建立机组在变工况时的能效模型[4]，但其采用的数据外插拟合精度难以控制，并且没有显示的计算公式，在一些应用领域难以满足数值精度要求。另外，上海交通大学的丁国良等建立了结合人工神经网络的翅片管式冷凝器快速仿真模型[5]，武汉第二船舶设计研究院的游加明等利用神经网络的非线性映射和泛化能力建立了一个冷凝器的BP神经网络模型[6]，但其采用的神经网络结构复杂，缺少统一的方程形式，并且计算时间较长。

混合建模是将先验知识和辨识建模方法结合在一起的一种“灰箱”建模策略，由于充分利用了过程的各种先验知识，从而降低了对样本数据的要求，使模型不仅具有良好的局部逼近性能，而且还有较好的全局性能，克服了传统非线性模型，如神经网络模型和模糊系统所存在的外延性差等问题。

PSO-RBF改进算法是在RBF神经网络算法和粒子群优化(Particle Swarm Optimization)算法(简称PSO算法)的基础上演化而来。相比于BP网络，RBF网络具有更好的泛化能力和逼近、拟合的能力，并且不存在局部极小点的问题，适合于建模设计，因此本文利用试验数据，采用RBF神经网络进行冷凝器机理模型优化。粒子群优化算法概念简单，实现方便，具有强大的全局搜索能力，对径向基神经网络的参数寻优具有良好的效果，因此采用粒子群优化算法用来寻求最佳的RBF参数可以解决RBF参数较难准确获取的问题[7-8]。在一般的粒子群优化中，都是对粒子的速度进行最大的限制约束，很少会对粒子位置进行约束限制。但是在径向基神经网络中，需要被优化的参数除了网络权值和阈值外，还有高斯中心和高斯宽度，而高斯中心和高斯宽度的取值一般只与网络的输入样本有关，因而针对径向基神经的参数特征，提出对粒子的位置向量进行分段限制策略，即PSO-RBF改进算法。

以某型舰用冷凝器为研究对象，在深入分析系统运行机理的基础上，建立冷凝器机理模型，根据实船的历史运行数据，采用PSO-RBF改进算法对冷凝器机理模型进行修正完善。所提方法以冷凝器机理模型为基础，能够较好地描述冷凝器的工作原理和特性，又以数据驱动的方法，充分利用实船历史数据，提高了模型的泛化能力，避免了装置长时间运行后，状态慢慢发生变化，模型精度逐渐降低的问题，具有较高的理论及工程应用价值。

2 冷凝器运行机理模型

为准确分析冷凝器热交换该过程，将冷凝器机理模型分为冷凝器壳体、冷却水流动换热过程两部分，如图1所示，并根据过程的复杂程度，分别采用集中参数法和分布参数法进行建模[9]。

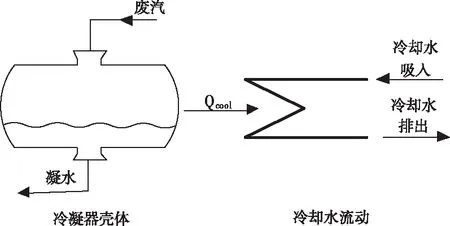
图1 冷凝器系统建模原理图

2.1 冷凝器壳体建模

采用集总参数法建立冷凝器壳体流动放热过程：

质量平衡

d(M)=ws-wc

(1)

能量平衡

d(E)=wshs-wchl-Qcond

(2)

冷凝器金属能量平衡

d(Em)=Qcond-Qcool

(3)

Qcond=hcAc(Ts-Tm)

(4)

式中：M为冷凝器内蒸汽及冷凝水的总质量，ws为废汽进口流量，wc为冷凝水出口流量，E为冷凝器内总能量，hs为废汽焓值，hl为冷凝水焓值，Em为冷凝器金属总能量，Qcool为蒸汽与冷却水管路的热交换量，Qcond为冷凝器金属吸热量，hc为蒸汽与管壁之间的换热系数，Ac为冷凝面积，Ts为蒸汽温度，Tm金属平均温度。

2.2 冷却水流动换热过程建模

冷却水在冷凝器管路中流动，吸收废汽传给金属管的热量，如图2所示。为准确分析冷却水吸热情况及温度变化，考虑流体参数在空间域的分布，采用分布参数法建立冷却水在管路中一维流动的吸热模型，并作系列假设[9-10]。

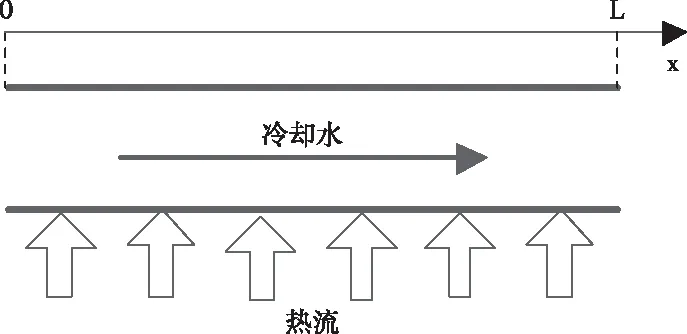
图2 冷却水一维流动换热

换热过程质量守恒、能量守恒和动量守恒模型分别为

(5)

(6)

(7)

式中：A为管路截面积，ρ为流体密度，w为质量流量，z为管路直径，S为圆周长，φext为热流量，g为重力加速度，h为冷却水比焓，v为冷却水比体积，Cf为摩擦系数。

3 PSO-RBF改进算法的冷凝器建模

3.1 冷凝器模型优化方法

在建立冷凝器机理模型的基础上，采用RBF神经网络建立冷凝器的辨识模型，并采用粒子群优化算法寻求最佳的RBF参数。但是在径向基神经网络中，需要被优化的参数除了网络权值和阈值外，还有高斯中心和高斯宽度，而高斯中心和高斯宽度的取值一般只与网络的输入样本有关，因此提出了PSO-RBF改进算法，即在寻优过程中，对粒子的速度进行最大的限制约束的同时，对粒子的位置向量也进行了分段限制。

3.1.1 RBF神经网络

在径向基神经网络中，输入向量直接通过径向基函数映射到隐含层，在这之间无需连接权值的调整，因此RBF神经网络的结构一般只有三层，一层输入层，一层为隐含的径向基层，另一层为线性输出层。其网络结构如图3所示。

图3 RBF神经网络

第一层为输入层，输入向量Xk=(x1k，x2k，…，xmk)T为与转速预测有关的变量，其中m为输入数据的维数，k=1，2，…，n为输入数据的个数。

第二层为隐含层，由I个神经元组成，接受输入层数据，隐含层选用高斯函数作为径向基函数，隐含层输出由输入向量与径向基函数中心之间的距离确定，当网络输入为Xk时，隐含层输出为

(8)

其中：ci为高斯函数的中心向量，σi为第i个高斯函数的宽度。

第三层为输出层，它对输入模式的作用做出响应，从隐含层的输出R(xi)到输出层y是线性映射，即

(9)

其中wi为隐含层与输出层之间的权值。

3.1.2 PSO-RBF改进算法

粒子群算法优化RBF网络的主要方法是用粒子群算法搜索RBF网络中的关键参数的全局最优值，流程如图4所示。

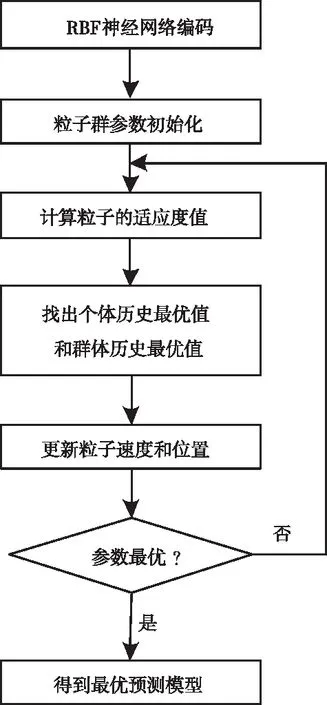
图4 粒子群优化RBF神经网络流程

具体步骤如下：

根据RBF神经网络的参数分析可知，在径向基神经网络中，高斯中心的位置必然位于输入样本之间，高斯宽度的最大值也要尽量小于样本的最大差值；而从一般确定径向基神经网络权值和阈值的方法中可以发现，网络的权值和阈值一般不超过输出理想值[11]。在粒子群优化径向基神经网络中，径向基神经网络的参数直接对应着粒子群的位置向量，因而对粒子群的位置向量提出如下策略

(10)

式中，W(j)表示粒子群的位置向量，P、T分别为网络的输入数据和理想输出数据，N为输入样本的总长度。前1～n维的粒子对应着高斯中心，取值范围为输入样本的最大值和最小值；n+1～m维的粒子对应着高斯宽度，范围最大值取输入样本最大值与最小值之差，范围最小值取输入样本最大值与最小值之差的1/N倍；m+1～K维的粒子对应着网络权值和阈值，取值范围为理想输出样本的正、负最大值。

在粒子群优化径向基神经网络中，除了对位置向量作出改进外，选择合适的惯性权重和加速因子也可以使得网络获得更好的优化性能。由于径向基神经网络具有良好的局部逼近能力，没有BP网络易陷入局部极小值的缺陷，因而对惯性权重和加速因子做简单的非线性动态调整即可，其权重动态调整公式可表示为

(11)

加速因子的动态调整公式表示为

(12)

式中，ωmax、ωmin为权重的最大值和最小值，cmax、cmin为加速因子的最大值和最小值，iter为当前迭代次数，itmax为最大迭代次数，a、b为常数。

3.2 预测模型的建立

利用粒子群优化后的RBF神经网络建立冷凝器主要参数的预测模型：

1)冷凝器真空度预测模型

冷凝器真空度影响因素包括当前冷凝器真空度、冷却水流量、排汽量、排汽温度、排汽比焓、排汽阀开度，定义上述参数变量符号分别为Pv、wc、wv、Tv、hv、E。根据经验取输出的真空度的反馈阶次为2，冷却水流量时延阶次为1，排汽阀开度时延阶次为1，其余参数不设时延，得到冷凝器真空度预测模型方程为：

Pvt+1=F(Pvt，Pvt-1，wct，wct-1，wvt，wvt-1，Tv，hv，Et，Et-1)

(13)

因此在冷凝器真空度的RBF神经网络模型中，网络输入为(Pvt，Pvt-1，wct，wct-1，wvt，wvt-1，Tv，hv，Et，Et-1)，输出为下一时刻的真空度。

2)冷凝器凝水温度预测模型

冷凝器凝水温度的预测主要与排汽量大小、冷却水流量、排汽温度和比焓以及排气阀开度有关，按真空度预测模型定义上述参数变量符号。根据经验取输出的凝水温度反馈阶次为1，冷却水流量时延阶次为1，排汽阀开度时延阶次为1，其余参数不设时延，得到冷凝器真空度预测模型方程为

Tt+1=F(Tt，Pvt，wct，wct-1，wvt，wvt-1，Tv，hv，Et，Et-1)

(14)

因此在冷凝器真空度的RBF神经网络模型中，网络输入为F(Tt，Pvt，wct，wct-1，wvt，wvt-1，Tv，hv，Et，Et-1)，输出为下一时刻的凝水温度。

3.3 结果分析

试验过程中，记录其在主机尾轴转速280r/min降低至主机尾轴转速180r/min过程数据。将工况转变过程中废汽排汽量、温度、比焓，冷却水流量、温度等历史数据作为冷凝器模型的输入，分别采用机理模型和基于PSO-RBF改进算法的RBF神经网络模型计算冷凝器真空度及凝水温度，并与试验结果进行对比，以验证模型的有效性。

编程过程中，RBF网络的隐含层的中心数目取12，PSO参数分别为：c1=c2=2.0，粒子种群数为50，最大迭代次数为200次。图5所示为两种模型的计算结果与试验数据的比较，其中图5(a)为冷凝器凝水温度的仿真结果，图5(b)为冷凝器真空度仿真结果。

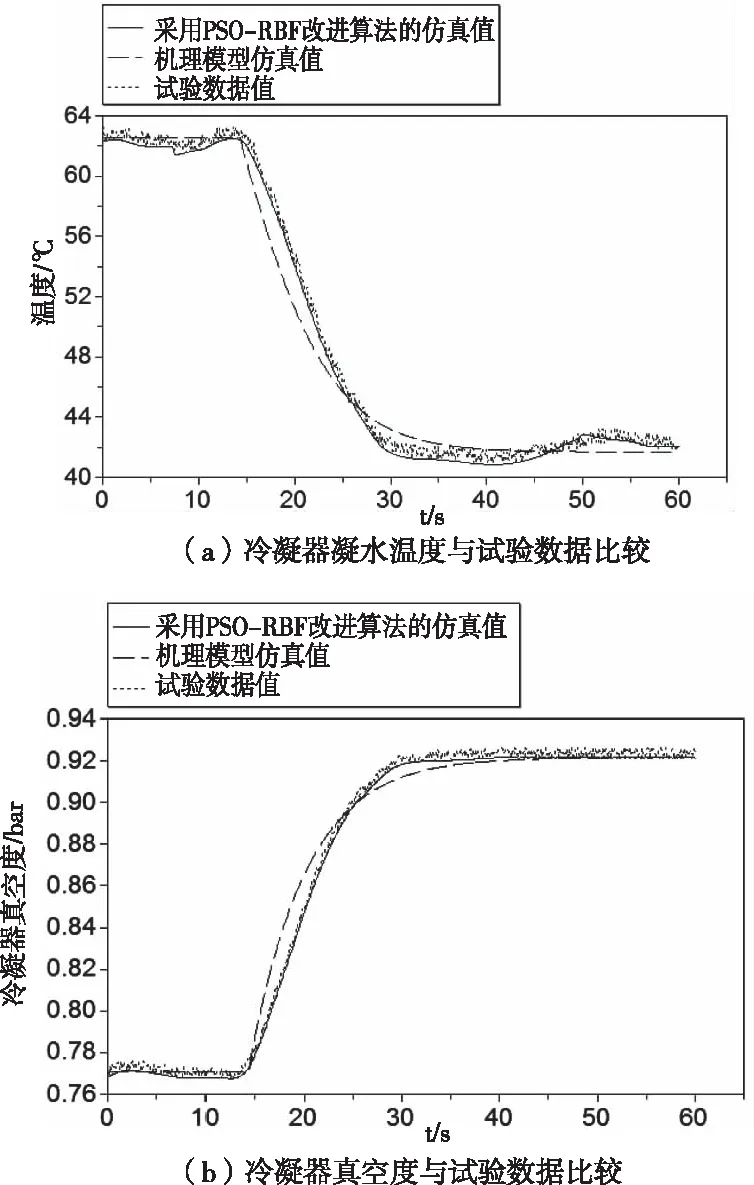
图5 2种模型计算值与试验数据比较

从图5中可以看出，机理模型的仿真结果与RBF神经网络的训练结果都与试验数据比较吻合，并且可以明显看出，采用PSO-RBF改进算法的神经网络模型的仿真结果，其适应度和拟合精度都较机理模型高，其建模思路是正确的，可以认为所建立的冷凝器辨识模型与实际设备具有一致的输出响应。

4 冷凝器运行特性分析

通过采用PSO-RBF改进算法经神经网络训练所得的冷凝器动力学特性计算模型可以作为部件模型存入该舰动力装置的计算模型库中，通过模型的搭接，构建该舰主动力装置总体性能仿真模型。通过对模型中其它部件的控制，可以分析该冷凝器模型在其各种工况下的动态特性。分析研究了汽轮机额定工况下转速负向阶跃20%以及冷却水流量负向阶跃20%，冷凝器部分参数包括冷凝器真空度、凝水温度、蒸汽凝结量、冷却水出口温度的动态响应。设置仿真时间为60s，仿真开始时刻投入系统控制参数的阶跃信号，研究冷凝器各参数的动态响应，仿真结果如图6所示。

图6 冷凝器在汽轮机转速、冷却水流量影响下的动态响应曲线

5 结论

本文以某型舰用冷凝器为研究对象，提出了一种基于机理和历史运行数据的两阶段建模方法，在机理模型的基础上，利用实船历史数据，采用RBF神经网络建立了冷凝器辨识模型，进行了仿真，分析了不同状态下冷凝器主要性能参数的动态特性。所得结论如下：

1)基于PSO-RBF改进算法的模型辨识属于一种灰箱建模方法，在给定的历史运行数据的基础上能够建立拟合度较高的计算模型，可以作为部件级的数学模型，对动力装置系统的总体性能进行预测和实时分析。

2)通过与实测数据相比，证明了模型具有较高的精度，可用于分析不同状态下冷凝器主要性能参数的动态特性，分析结果可为冷凝器的优化设计和控制策略的制定提供参考。