基于CVAE的超高速碰撞碎片云运动过程的快速预测技术

2021-11-19李毅任磊生

实验流体力学 2021年5期

周浩，李毅,*，张浩，陈鸿，任磊生

1.中国空气动力研究与发展中心超高速空气动力研究所，四川绵阳 621000 2.中国工程物理研究院计算机应用研究所，四川绵阳 621000

0 引言

人类航天活动形成了大量空间碎片，这些空间碎片速度能够达到几公里每秒甚至十几公里每秒[1]，严重影响航天器安全，因此需要采取必要防护措施。目前主流的防护技术是Whipple 屏[2]及其改进防护屏技术，该技术是在航天器舱壁前一定距离处设置一防护屏。在空间碎片超高速撞击防护屏产生的高温高压下，弹靶材料撞击区呈流体状态，破碎后形成扩张的碎片云，使入射弹丸动能被高度分散并部分耗散，从而实现对航天器的有效保护。由于碎片云的形状、速度和质量分布对其后续侵彻舱壁的过程具有重要影响，在很大程度上决定了防护屏的防护能力，因此，快速预测弹丸超高速撞击防护屏产生碎片云的质量分布及其随时间变化规律具有重要意义。

在弹道靶上开展地面超高速撞击试验是获取不同防护屏设计方案中碎片云分布特征的最有效方法，但试验存在成本、效率、测量难度以及参数范围限制等一系列问题。数值模拟具有成本低、获取数据丰富的优点，目前已成为研究碎片云的重要手段，但数值模拟同样存在效率低的问题，难以完全满足空间碎片防护分析设计的需求。为此，学者们提出了很多工程模型来快速预测碎片云特性。Swift 等[3]将碎片云简化为质量均匀分布的球形；Schäfer[4]将碎片云分为3 个部分（一个质量均匀分布的椭球壳、一个质量均匀分布且内切于椭球壳的球壳和一个位于碎片云前端的大碎片），如图1（a）所示。此外，还有一些更加复杂的改进方案[5-7]，如Huang等[6]从碎片云中碎片特征（质量、速度和空间角度等）的统计规律出发，采用蒙特卡罗抽样方法，构建了一个碎片云工程模型，如图1（b）所示。这些工程模型虽然计算效率高，但存在过度简化问题，碎片云形态比较粗糙，而且一般忽略了反溅碎片云。

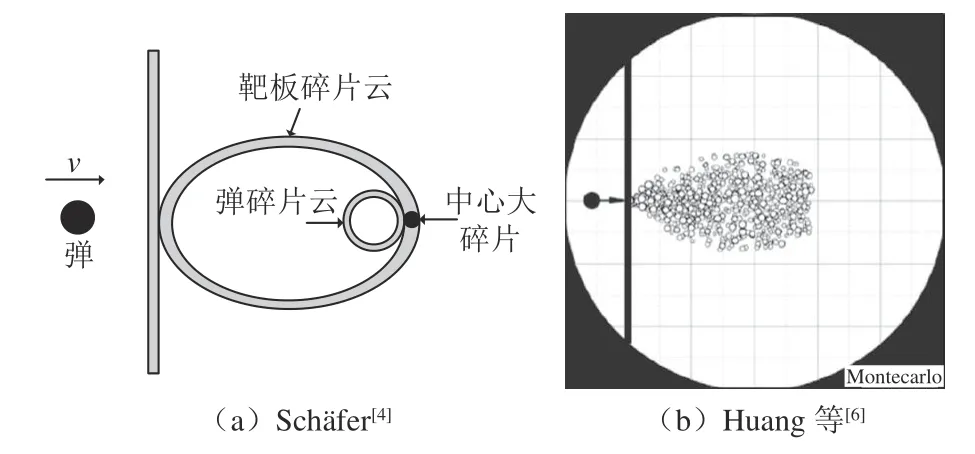
图1 典型超高速碰撞碎片云工程模型Fig.1 Typical HVI debris engineering model

当前，基于大量试验和模拟数据的深度学习建模技术被广泛应用于航空航天与国民经济的各个方面，在工程预测的精度或效率方面明显优于传统方法。在空间碎片防护领域，深度学习建模技术也开始在铝板防护设计优化[8]、弹丸穿靶后在平板上形成的入射孔径的大小预测[9]、弹丸在平板上成坑、穿孔等不同损伤模式预测[10]等方面得到初步应用。CVAE[11-12]是一种经典的应用于图像生成的深度学习模型，其基本功能是根据给定的标签生成样本，现已成功应用于湍流模拟[13]、外形阻力系数优化[14]、蛋白质折叠模拟[15]、分子结构设计[16]等领域。预测给定条件（如弹丸速度、弹丸大小、防护屏厚度、观测时间等）下的碎片云二维质量分布，其过程与CVAE 模型的作用非常类似，且碎片云二维质量分布刚好可以用一张灰度图来表示。此外，深度学习需要大量训练数据，而中国空气动力研究与发展中心依托大型弹道靶设备，积累了大量超高速撞击试验数据，且初步建设了试验大数据系统。因此，本研究团队对采用CVAE 模型从大量数据中提取规律进行了初步尝试。由于大量试验数据的格式不统一，且某些数据信息不全（如受限于试验测试能力，无法定量得到碎片云中的质量分布），因此，在对代码进行必要验证的前提下，暂时采用数值模拟方法生成大量格式统一的数据进行训练，以初步验证方法的可行性。本研究团队前期模拟了大量弹丸超高速碰撞典型航天器部件的问题，分析了弹丸速度、碰撞角度以及撞击点偏差3 个变量对固定时刻碎片云质量分布的影响。在数值模拟结果中，利用碎片识别程序提取出碎片云中所有碎片的质量和位置信息，从而得到碎片云二维质量分布，并将其作为训练样本。在此基础上构建了CVAE 深度学习模型[17]，用于预测固定时刻的碎片云质量分布，结果表明：预测精度远高于传统的工程模型，而且计算效率远高于数值模拟。

本文在前期研究的基础上，进行了以下改进：1）考虑了时间因素，从而可以预测碎片云的发展变化过程，这也就隐式地给出了碎片云中部分速度信息。2）训练样本直接从每个SPH 粒子得到，而不是从碎片识别数据（质量和位置）得到，大幅提高了输入数据的精度。因为有些大碎片尺寸超过了背景网格，将此碎片质量全部计入其质心位置所在网格与事实不符，会导致样本精度不高。此外，由于碎片质量差别过大，前期研究中还剔除了尺寸最大的碎片，导致碎片云中没有防护屏的位置信息。3）由于弹丸速度差别较大，因此碎片云的分布区域差别也较大。为了减少图像中的空白区域，增加图像中的信息量，前期研究中对碎片云按速度进行了缩放。人为缩放后更加容易训练，但是导致每个网格的预测结果缺少统一的物理意义。此外，缩放后再还原到物理空间实际上就隐含了碎片云实际范围正比于速度的物理意义。人为缩放相当于只考虑碎片云的形状，而忽略碎片云的实际大小。本文在一个足够大的固定空间中统计碎片云质量分布，让模型自主学习碎片云的所有运动规律。4）精简网络结构，采用全局平均池化技术代替部分全连接层，将参数总量由近2000 万降至500 万以下。

1 数据与模型

1.1 数据集

考虑球形铝弹丸超高速正撞击铝防护屏过程中的碎片云发展过程。研究影响碎片云形状的4 个控制条件，即入射速度（v）、防护屏厚度（d）、弹丸半径（r）以及观测时间（t）。输入数据由PTS 软件[18]批量计算，采用的数值方法为光滑粒子流体动力学（SPH）方法。以（最小值、间隔、最大值）表示变量取值范围，则入射速度范围为（3.00 km/s、1.00 km/s、8.00 km/s），防护屏厚度范围是（1.000 mm、1.000 mm、4.000 mm），弹丸半径范围是（2.00 mm、1.00 mm、8.00 mm），观测时间范围是（1.0 μs、1.0 μs、12.0 μs）。以2016 个数据作为训练集，在其中随机抽取1%作为验证集。

典型的超高速碰撞碎片云发展过程的试验结果如图2 和3所示[19]。在图2 中，圆柱锌弹丸的半径为1.99 mm，长度为14.15 mm，入射速度为4.97 km/s，锌板厚度为0.965 mm，观测时间为10.5 μs。在图3 中，圆柱铜弹丸半径为5.59 mm，长度为3.45 mm，入射速度为5.55 km/s，防护屏材料为铝，厚度为2.870 mm，观测时间为6.4 μs。图2 和3 中同时也给出了对应时刻的PTS 软件模拟结果。图4 给出了中国空气动力研究与发展中心测试得到的典型碎片云序列阴影图像以及PTS 软件模拟结果[20]。其中，铝弹丸的半径为3.00 mm，入射速度为8.31 km/s；防护屏材料为铝，厚度为2.000 mm。可以看到，PTS 软件模拟的碎片云轮廓与试验基本一致。因此，本文暂采用PTS 软件模拟得到的碎片云质量分布作为训练集。

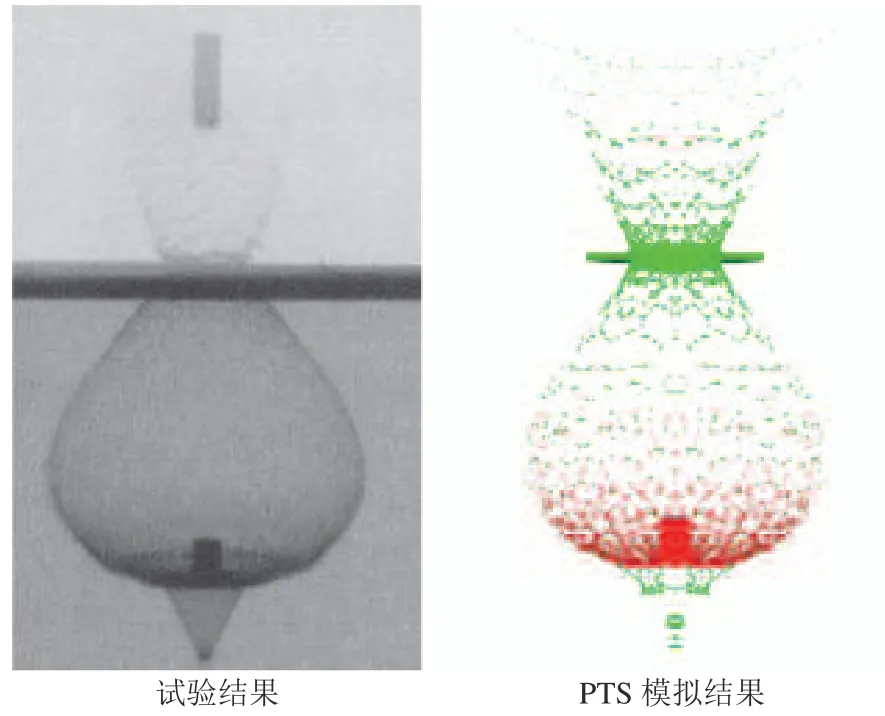
图2 锌弹丸超高速撞击锌板Fig.2 Zinc projectile impact Zinc plate

图3 铜弹丸超高速撞击铝板Fig.3 Copper projectile impact aluminum plate

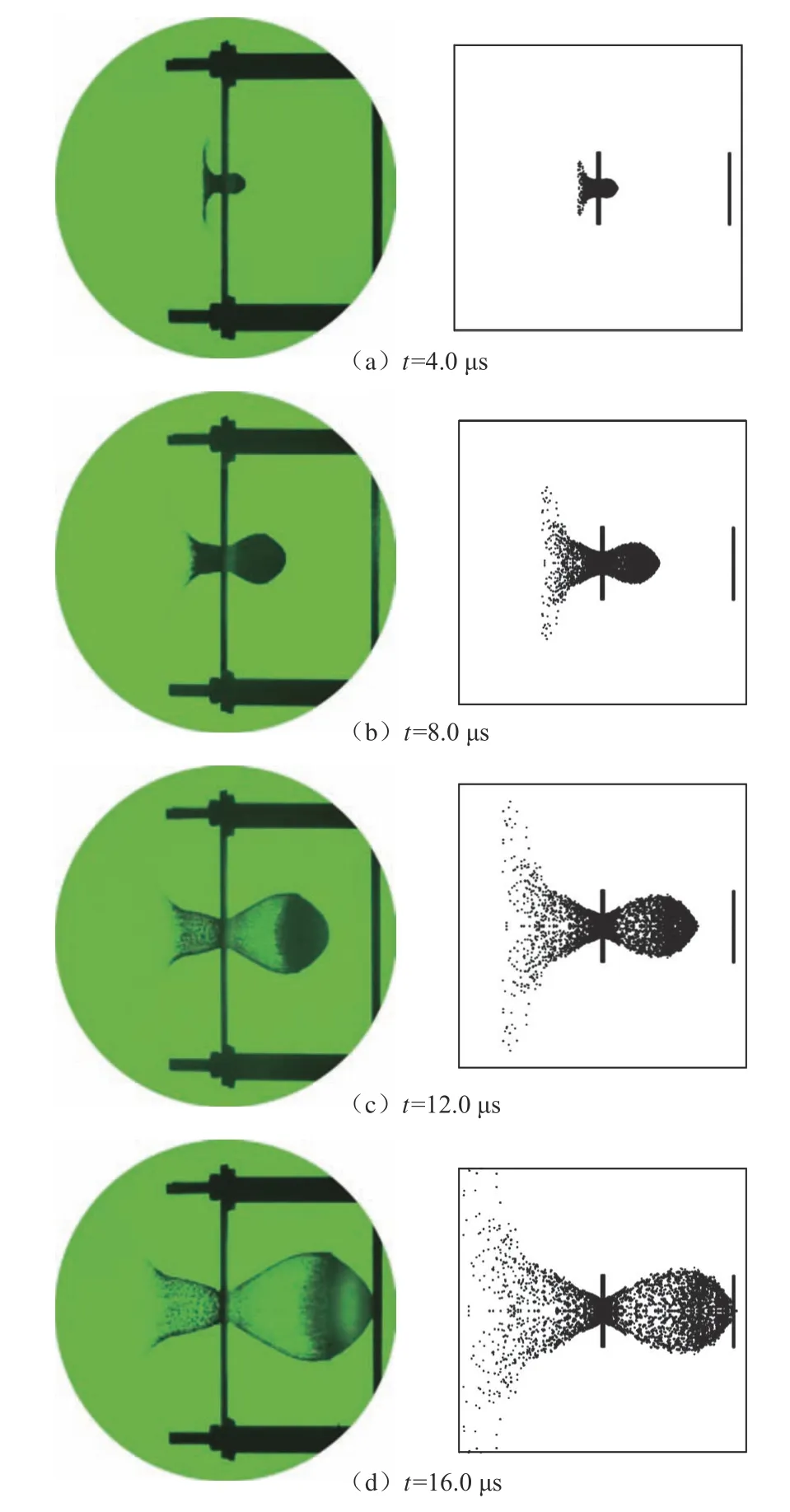
图4 典型超高速碰撞碎片云发展过程试验（左）与SPH 数值模拟（右）结果对比Fig.4 Comparison of experiment and SPH simulation for a typical HVI impact

忽略反溅碎片云后部质量较低的区域，仅考虑x轴范围为–4～10 cm、y轴范围为–7～7 cm 的方形区域（以弹丸入射位置为坐标原点）。将该区域划分为100×100 的网格，统计每个网格中的总质量，以这10000 个质量数据表征碎片云的质量分布。由于每个网格中质量数据差别很大，对其取对数，并以全局最小和最大网格质量为标准进行归一化。网络的输出层采用sigmoid 激活函数，因此模型预测结果是归一化的，参考同样的全局最小和最大网格质量可将其还原为真实质量。

1.2 CVAE 模型构建

根据CVAE 基本原理，本文构建了如图5所示的碎片云生成模型。在编码器中，将碎片云质量分布数据及其标签（弹丸速度、板厚、弹丸半径和时间）采用Concatenate 层连接在起来，形成一个100×104 的矩阵，其中最后4 列为控制条件；然后通过一系列卷积层（Filters = 1、16、32、64、128、256）提取不同层次的图像特征；使用全局平均池化技术降维，并用两个全连接网络生成样本的均值和方差，最后高斯抽样得到隐藏层数据。在解码层，同样采用Concatenate 层将隐藏层输入和隐藏层标签连接起来，采用全连接层升维，最后采用一系列反卷积层（Filters = 512、256、128、96、1）得到原始图片。损失函数由两部分组成：第一部分描述生成图像与训练样本的相似度，用交叉熵表示；第二部分描述隐藏空间的分布与标准正态分布的相似度，用KL散度表示。

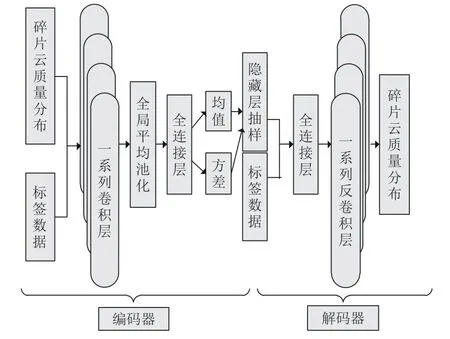
图5 CVAE 模型Fig.5 Structure of the CVAE model

CVAE 模型实现采用Keras 函数库，后台使用TensorFlow 深度学习框架执行模型训练。模型优化使用Rmsprop 算法，参数为默认参数。训练过程共执行1000 个Epochs，训练集误差与验证集误差曲线如图6所示。

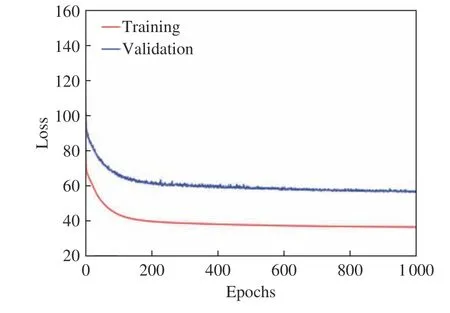
图6 CVAE 模型训练过程Fig.6 Training of the CVAE model

2 模型评估

2.1 模型还原能力

考察模型复现训练集数据的能力。取弹丸速度8.00 km/s、半径2.00 mm，板厚4.000 mm。此时，弹丸较小、板较厚，弹丸破碎比较严重。图7 比较了在此参数下的数值模拟和CVAE 模型预测的碎片云发展情况，其中上为预测结果，下为数值模拟结果。

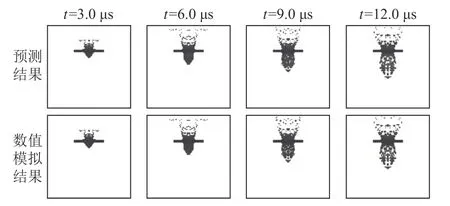
图7 碎片云发展过程的CVAE 模型预测与数值模拟结果对比（v =8.00 km/s，d = 4.000 mm，r = 2.00 mm）Fig.7 Comparison of the CVAE model prediction and numerical simulation of the evolution of debris(v = 8.00 km/s，d = 4.000 mm，r =2.00 mm)

取弹丸速度为8.00 km/s、半径为8.00 mm，板厚为1.000 mm。此时弹丸较大、板较薄，弹丸破碎不严重，形成了一个中心大碎片。数值模拟和CVAE 模型预测对比如图8所示。

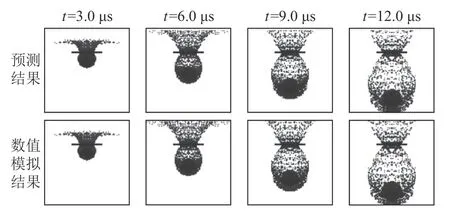
图8 碎片云发展过程的CVAE 模型预测与数值模拟结果对比（v=8.00 km/s，d = 1.000 mm，r= 8.00 mm）Fig.8 Comparison of the CVAE model prediction and numerical simulation of the evolution of debris(v = 8 km/s，d = 1 mm，r = 8 mm)

从图7 和8 可以看到，深度学习模型预测的碎片云质量分布图像比较逼真，精度远高于传统工程模型。假设每个碎片的速度变化不大，则碎片云的外形尺寸应大致正比于弹丸速度和观测时间。这一结论与图7 和8 定性相符，说明本文CVAE 模型能够自主学习到这一基本结论。

为了定量描述模型的精度，需要定义每个网格内的相对误差。很多网格内的质量为0，而所有输入数据中防护屏内部网格质量是常数，可以选为基准。定义每个网格质量相对百分比误差和总体平均误差分别为

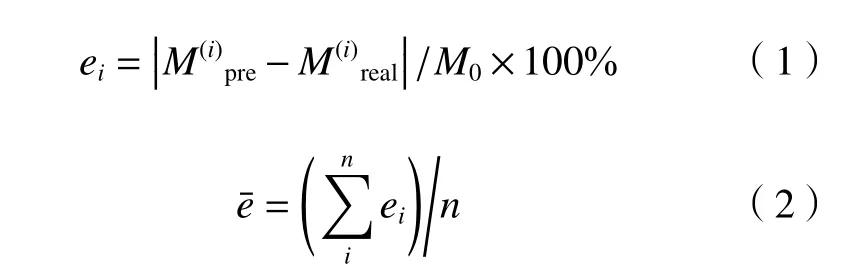
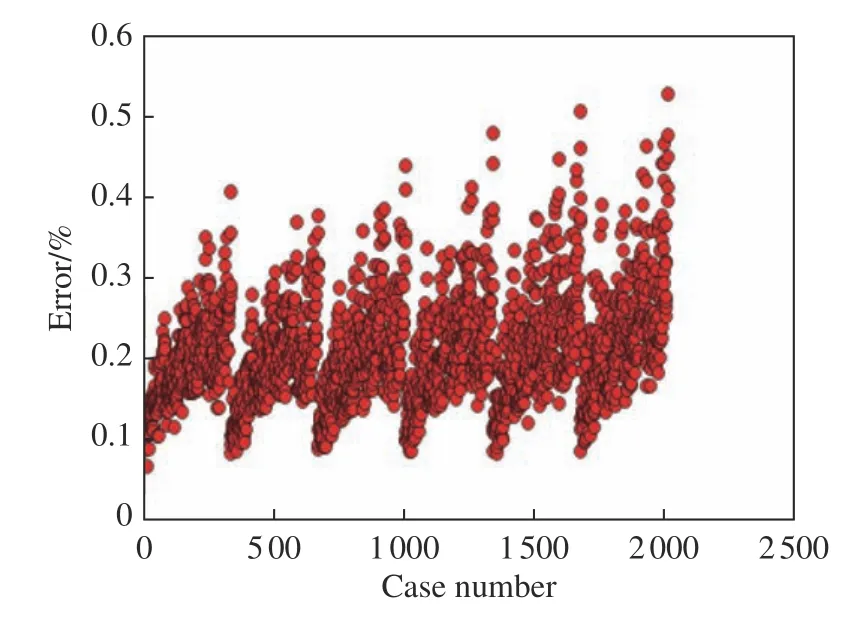
图9 训练集中2 016 个数据的平均误差Fig.9 Average error of 2 016 data on the training set

2.2 模型内插能力

取板厚1.000 mm、弹丸半径8.00 mm、观测时间12.0 μs，考察模型在入射速度6.00～7.00 km/s 之间的插值能力，如图10所示。可以看到，插值结果连续且稳定。碎片云长度随着速度增大而增大，与事实吻合。

图10 模型在速度上的内插能力（d = 1.000 mm，r = 8.00 mm，t=12.0 μs）Fig.10 Interpolation capability of the model at the velocity direction(d = 1.000 mm，r = 8.00 mm， t = 12.0 μs)

为了定量考察模型的内插能力，取速度范围（3.50 km/s、2.00 km/s、7.50 km/s）、防护屏厚度范围（1.500 mm、1.000 mm、3.500 mm）、弹丸半径范围（3.50 mm、2.00 mm、7.50 mm）、观测时间范围（1.5 μs、3.0 μs、7.5 μs）内的81 个数据作为测试集。误差在0.6%以内，如图11所示。由于时间是影响平均误差最大因素，而测试集的最大时间仅到7.5 μs，导致测试集误差反而略小于训练集。

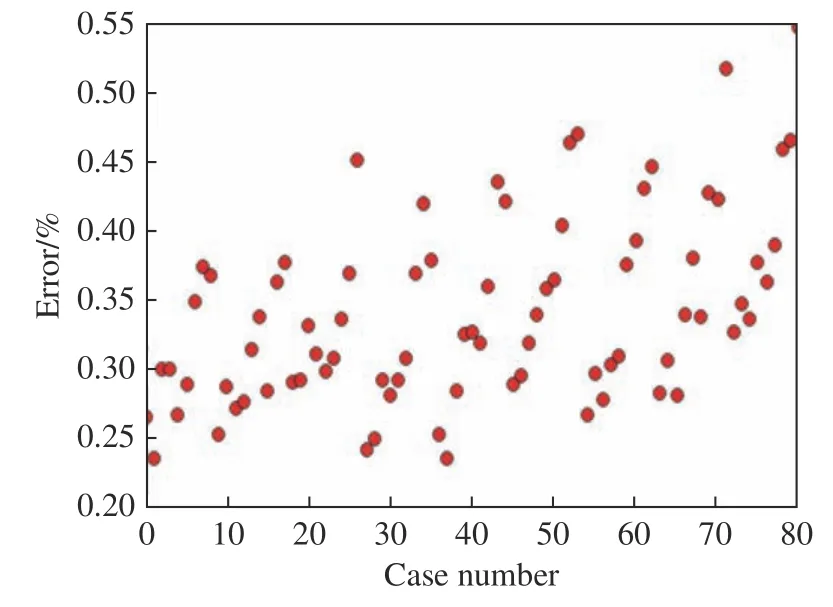
图11 测试集中81 个数据的平均误差Fig.11 Average error of 81 data on the testing set

2.3 模型外插能力

为了考察模型在训练参数范围以外的泛化能力，取弹丸速度8.00～9.00 km/s，板厚1.000 mm，弹丸半径8.00 mm，观测时间6.0 μs。预测结果如图12所示，当速度大于8.00 km/s 时，碎片云长度并未随着速度的增大而增大，可以看出，本模型在外推方面具有一定局限性。

图12 模型在速度上的外插能力Fig.12 Extrapolation capability of the model at the velocity direction

2.4 模型训练与预测效率

在NVIDIA K6000 GPU 卡上训练1000 个Epochs大约需要14 h。加载已经训练好的模型后，在i7-6700 CPU、内存8 G 的台式机上生成1 个碎片云图像的平均时间小于7 ms。

2.5 模型局限性

本文目前仅考虑了碎片云二维质量分布，进一步提高训练效率后可以推广到三维。为了提高训练效率，本模型仅考虑了铝材料和正碰撞，实用性还有待提高。下一步，可以将弹丸和防护屏的力学性能参数（如材料密度、声速、剪切模量以及屈服强度等）以及弹丸着靶姿态考虑进去。本模型在外推方面还具有局限性，需要对本文模型的结构进行改进。