一种小推力航天器变轨优化方法

迟进梓 余红英 张子雄

中北大学，太原 030051

0 引言

目前，化学燃料推进和电推进是航天器的主要推力来源[1]。由于化学燃料推进方式比冲小，能量密度低，在执行任务时，携带大量推进剂，增加了卫星发射成本[2]。而电推进属于小推力推进方式，由于其具有比冲大、控制精度高等特点，提高了探测器有效载荷的比重，具有优秀的研究应用前景[3]。电推进技术[4]是利用电力技术使推进剂膨胀，向后高速喷发，产生航天器所需推力的技术，适用于速度矢量较大以及保持轨道精度等变轨情况。

使卫星等航天器从原轨道转移至期望轨道上，此过程称之为轨道机动[5]，本文针对小推力类轨道机动的轨道转移问题进行研究。针对卫星等航天器模型的变轨问题，Kluever[6]提出了一种电推进轨道转换权衡的算法，主要对化学-电混合推进的GEO轨道转移方案进行研究，实现了快速开展大推力轨道变换。Fakoor等[7]将解析方法与基于种群的人工蜂群算法相结合，通过人工蜂群算法搜索控制变量的初值和目标函数的终止时间，给出了轨道转移过程中状态和控制变量的变化率，所得结果具有相当的收敛性和足够的精度。Caillau等[8]对从GEO轨道到地月系L1点和月球轨道的航天器转移轨道进行相关研究，虽然能实现航天器的轨道转移，但此方法并未对小推力转移轨道优化问题进行研究。付磊等[9]建立了多冲量变轨模型，得到最优冲量的时刻和大小，解决了远程导引多冲量变轨问题。黎桪等[10]创造性地使用两次伪谱法优化小推力轨道，较好克服一次伪谱法在求解燃料最优时产生的震荡问题。Pontani等[11]联合使用VTD-NOG和PD-RM控制完成了低推力月球轨道转移。

本文提出一种新的轨道转移和规划算法，将小推力卫星变轨过程转化为最优控制中两点边值问题，然后针对该问题引入混合遗传算法进行解算，完成小推力航天器轨道转移，实现了对小推力航天器由低轨向高轨的飞行轨道规划和优化设计。

1 动力学模型

小推力航天器质量随燃料消耗而减小，在飞行时主要受到发动机推力与地球重力作用，而春分点轨道根数与春分点坐标系OE-xyz相联系，坐标系变换见文献[2]。经过计算，以春分点轨道根数和卫星的燃料质量[r′,xh,yh,n1,n2,λ,m]为状态量，不考虑摄动，改进春分点根数下的动力学模型为：

(1)

2 轨道转移优化问题

轨道转移优化是在已知航天器姿态以及初始状态情形下，并在航天器满足以春分点根数变分方程为基础的航天器运动方程条件下，通过优化算法得到变轨过程中燃料消耗和时长的最优解。

2.1 小推力航天器运动方程

本文用春分点根数变分方程表示航天器的运动方程：

(2)

以k=[r,xh,yh,n1,n2,λ]T表示t时刻轨道状态向量，k可表示为位置和速度的函数：

(3)

则有：

(4)

其中有：

(5)

P与m分别表示推力矢量与卫星的燃料质量，R为从地心到在轨服务对象的位置矢径。式(4)中的春分点根数相对于位置和速度的偏导数通过春分点根数间的泊松括号与位置速度对于春分点根数的偏导数联系起来，求得春分点轨迹根数矢量状态变分表达式：

(6)

由式(6)可知，求出春分点根数关于速度的偏导数，代入式(5)得到最终的轨道根数变分方程。

2.2 最优控制问题描述

小推力变轨机动的轨迹优化，本质上是求燃料消耗最少且用时最短的轨迹。由于研究问题的背景不同，约束条件不同，导致最优控制问题不尽相同，需利用数值方法得解析解。本文选取的优化量是推力方向矢量。而目标函数分为燃料消耗以及时间消耗两类。但如果变轨过程中持续推力一直为最大值，则两类目标函数效果是一致的。根据飞行任务，目标卫星最终状态要符合前期需求中的限定因素。在最短时间的约束条件下，其模型性能指标可表示为：

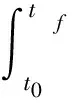
(7)

tf为最终时间，t0为初始时间。根据极大值原理以及式(1)中的燃料质量方程和式(2)，哈密顿函数(H函数)为：

(8)

式(8)中，λxT为协态变量矩阵，λλ和λm为协态变量。由最优控制理论可知，若要达到最优控制目标，需使H函数可在某区间内取到极小值。而由式(8)，航天器最佳推力方向应与矢量λxTN反向，即：

(9)

P应该满足约束：

0≤P≤Pmax

(10)

P应该在这一区间内使H函数取到极小值，将H对P求偏导，得：

(11)

为H取极小值，选取合适点火开关函数[12]。协态方程为：

(12)

δ和η分别为推力的方位角和高低角，由δ和η确定推力方向角。协态变量在函数中还需要受到截断因素的影响：

(13)

式(13)中，拉格朗日乘子用γ进行表示。由于tf自由，因此在最佳轨道时刻，哈密顿方程理应满足以下表达：

H[k*(tf*)，λ*(tf*)，P*(tf*),tf*]=

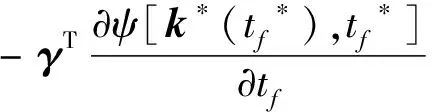
(14)

将式(8)、式(13)第二式代入式(14)可得：

(15)

式(7)～(13)一起组成最短时间约束条件下最佳目标参数函数方程组。本文求解该方程组思路是将状态变量和协态变量转化为两点边值问题，然后选用混合遗传算法进行求解。

3 算法流程

遗传算法具有较强的全局遍历能力，使时间效率得到有效提高，但其局部查找能力不强，而经典优化算法恰好具有与之相反的特点。因此本文取两者进行混合使用，使整个算法有良好的时间复杂度。

遗传算法是一种通过分析系统整体特征，产生具有自我优化参数能力的算法模型。由于当前模型的特殊性，惩罚函数进行如式(16)定义：

(16)

p为整数，通常取1或2。βj是表示约束权重的因子。dj(Z)=0(j=1,2,…,n)表示等式约束。广义适应度函数在惩罚函数约束下为：

F(Z)=J(Z)-φQ(Z)

(17)

式(17)中，φ为惩罚因子，当φ>0，φ→+∞时，原函数收敛得到最终结果。但因子系数较高或较低会导致结果与真实结果值相去甚远，甚至破坏种群更迭条件。因此，本文使用具有自我调节能力退火筛选函数约束：T=T0，种群中惩罚因子为：

(18)

式(18)中，μ∈[0,1]表示温度制冷速率常数；G代表种群繁衍层数，Tf是退火凝结温度。式(16)中的βj选择可以通过随机权重的方法进行获取：

(19)

式(19)中，lj是非负随机数。

4 仿真实验及结果

本章基于电推式小推力卫星轨道规划的理论基础，在开源科学工程计算软件SCILAB6.0.1上的SiROS下开发了仿真模块。并利用仿真模块搭建了GTO-GEO轨道转移仿真模型，对电推式小推力卫星变轨机动方案的优化算法进行验证。

4.1 仿真模型搭建

本文4个仿真模块是在SiROS下的宇航函数库中开发的，分别是模块1：初始轨道规划模块，模块2：轨道优化模块，模块3：轨道动力学模块，模块4：变轨制导控制算法模块。初始轨道规划模块封装及连接如图2所示。其是基于标称轨道法设计的，输出为小推力轨道优化结果，表示多圈小推力标称轨道上各分段节点的轨道根数初值。

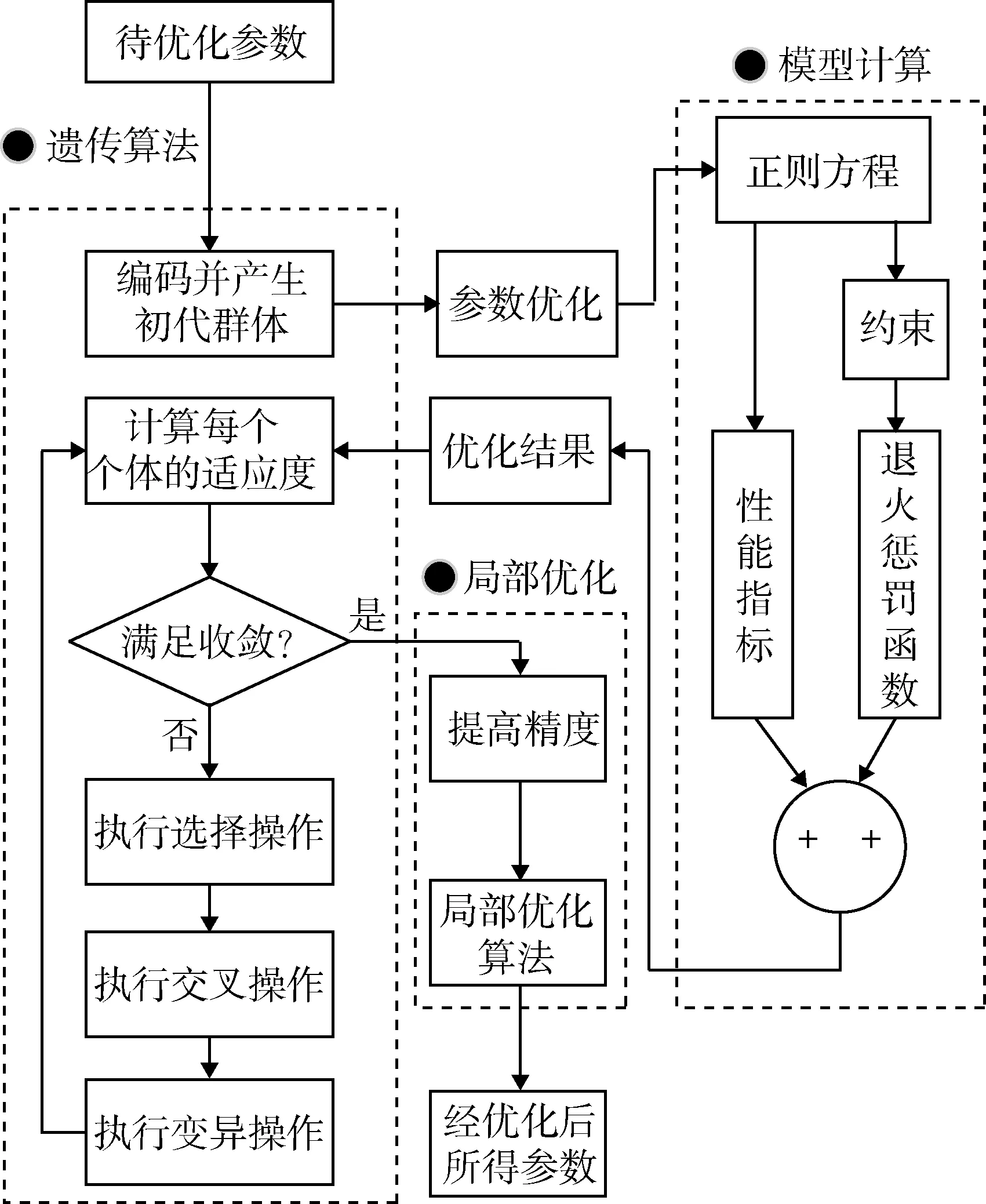
图1 混合遗传算法流程图

图2 初始轨道规划模块封装及连线

如图3所示为轨道优化模块封装及连接图，轨道优化设计模块是根据本文优化方法开发的，给出基于退火遗传算法得到的小推力轨道优化结果，其结果表示小推力轨道上各分段节点的轨道根数初值，参数值与初始标称轨道规划模块一致。

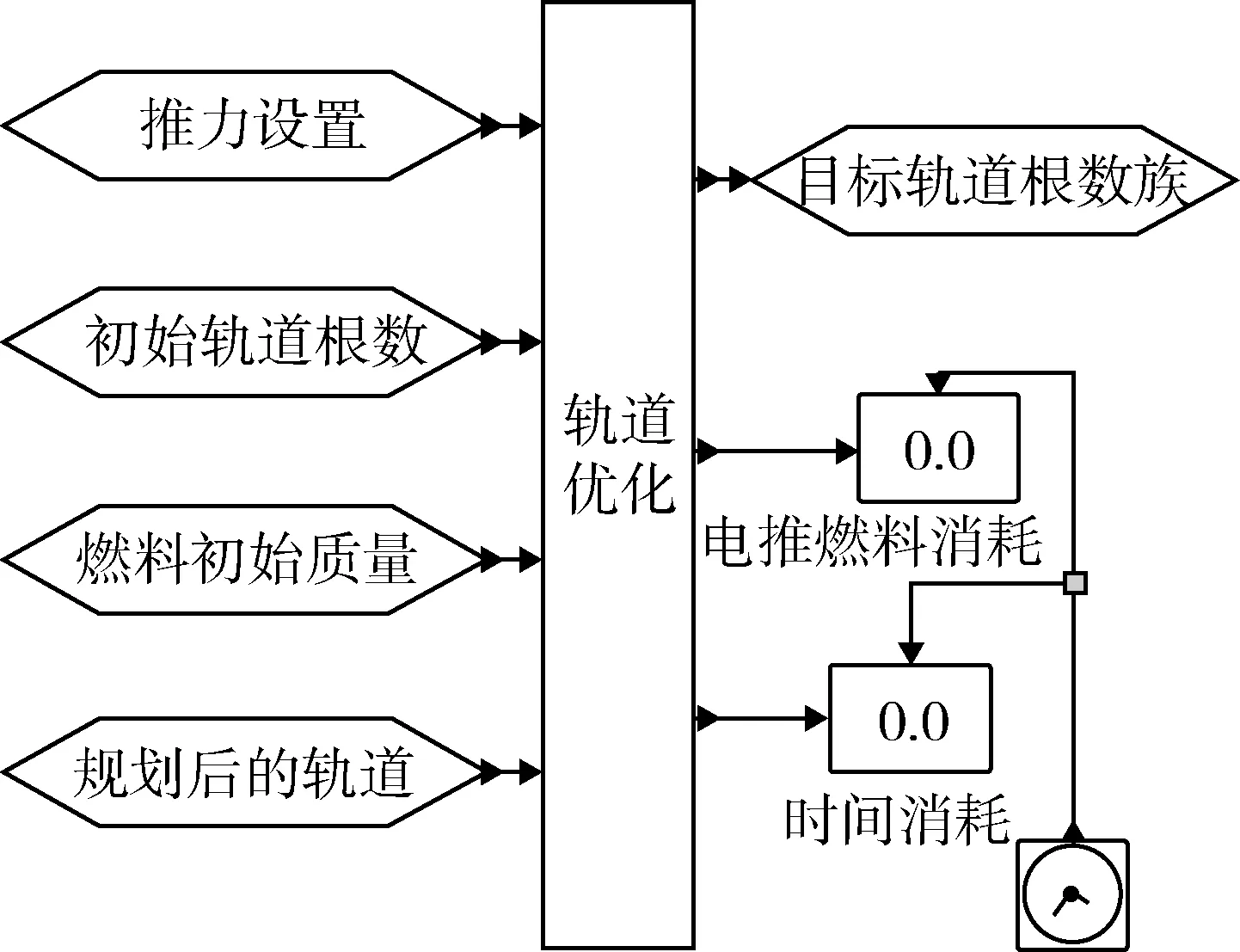
图3 轨道优化模块封装及连线

如图4所示为轨道动力模块封装及连接图，将该模块数据输入模块4，随仿真时间的推进不断计算新的轨道根数、飞行器质量、推力，直至仿真任务完成。该模块的摄动加速度设置为常量。

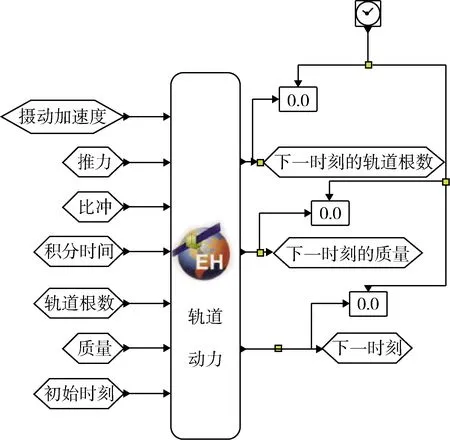
图4 轨道动力模块封装及连线

而变轨制导控制模块用来对规划好的轨道进行跟踪。变轨制导控制模块封装及连接如图5所示。

图5 变轨制导模块封装及连线

各模块需要配置参数如表1，输出参数如表2。

表1 各模块参数配置

表2 各模块输出参数

4.2 轨道转移仿真与分析

变轨开始时间为2020年1月1日0时0分，初始质量为1500 kg，电推力比冲为3800，推力方位角上限为6.28 rad，推力上限为1 N。GTO-GEO轨道转移仿真模型如图6所示，各参数如表3所示。

表3 模型各参数初值

图6 GTO-GEO轨道转移仿真模型图

为验证该算法的正确性和有效性，将本文所提方法解与最优解进行性能比较。图7为半长轴随时间变化图。图8为偏心率矢量随时间变化图，图9为倾角随时间变化图，图10为推力随时间变化图。虚拟小推力飞行器模型在2020年01月01日00时00分出发，携带的初始燃料质量为1500 kg，在2020年02月 13日21时36分到达，所用的时间是44.9天，消耗燃料为171.2 kg。

图7 半长轴随时间变化图

图8 偏心率矢量随时间变化图

图9 倾角随时间变化图

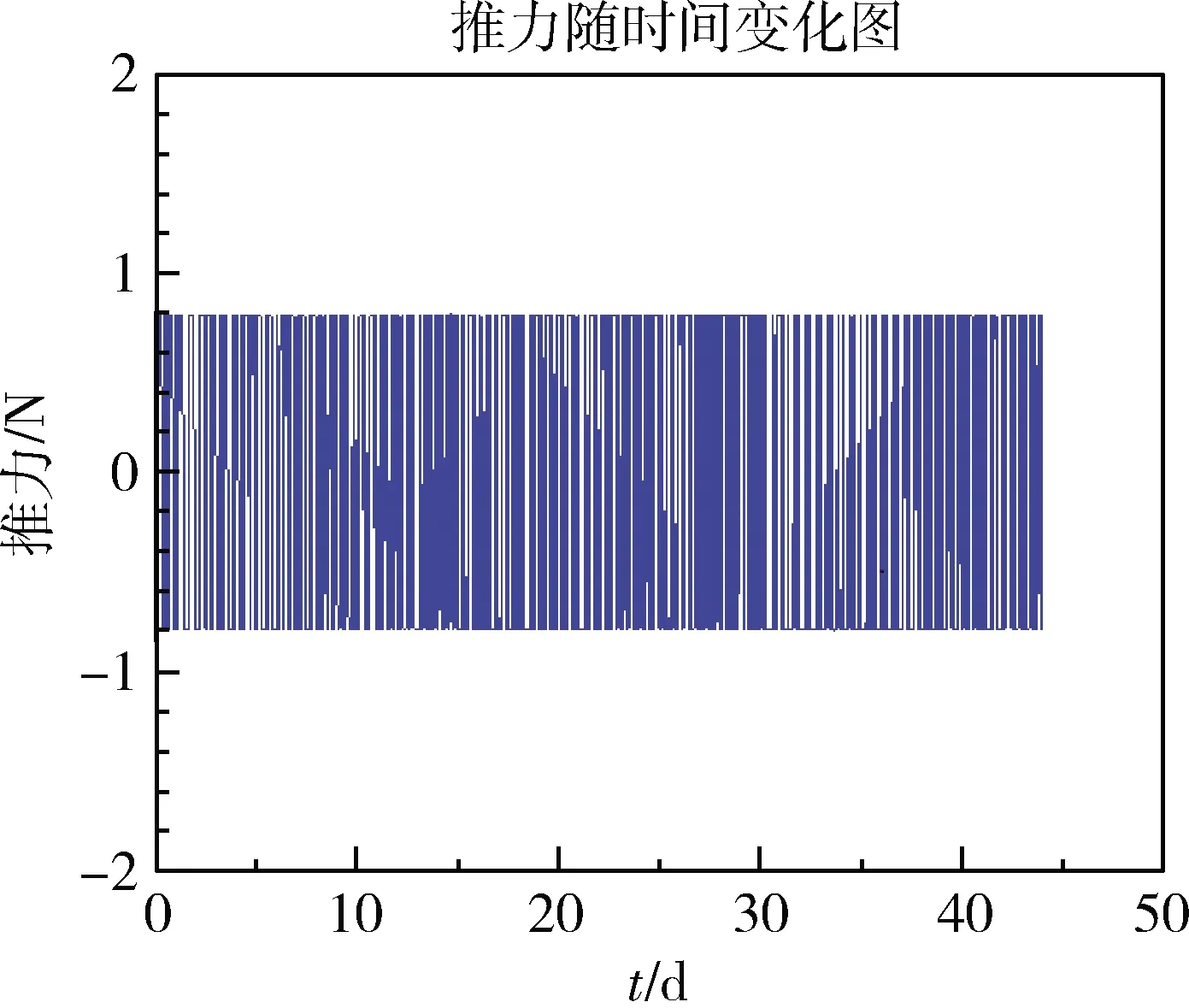
图10 推力随时间变化图

图11所示为推力示意图，其中Ux，Uy和Uz分别为径向、切向和法向小推力加速度，各推力分量变化如图12～14所示，推力方位角变化如图15～16所示。

图11 推力示意图

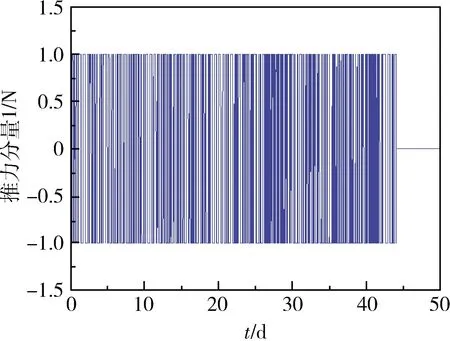
图12 推力分量1示意图

图13 推力分量2示意图

图14 推力分量3示意图

图15 推力方位角1变化示意图

图16 推力方位角2变化示意图

在航天器由GTO轨道转移到目标轨道时，由公式(1)可知，推力器产生的推力使轨道半长轴增大，轨道偏心率降低，轨道倾角减小。由图7～10可知，在小推力航天器进行轨道变换期间，偏心率矢量与轨道倾角单调下降，而半长轴单调上升，推力的方向和大小都成周期性变化，与理论分析相符。推力方位角1在[-45°，45°]范围内变化，推力方位角2在[-90°，90°]范围内变化，直至变轨结束。通过对GTO-GEO轨道转移的过程进行仿真与分析，可以得到仿真结果如表4所示。

其中，最优解结果是不考虑对轨道产生显著影响的摄动因素的结果，混合动力是本算法下化学燃料和电推进混合推进方式。由表4可知，本文所提算法消耗了占总质量的11.4%的燃料，在燃料消耗上，仅比最优解多1.2%，而相较于传统遗传算法，本文算法节省了3.7%的燃料，相较于混合动力模型，本文算法节省了10.7%的燃料。本文所提算法完成变轨用时44.9天，时间消耗上，仅比最优解多13.9%，而相较于传统遗传算法，本文算法节省了30.9%的时间，相较于混合动力模型，本文算法节省了19.8%的时间。由此可见，本文所提算法能顺利完成GTO轨道至GEO轨道的转移任务，各模块运行正常，能以接近于最优控制解的结论完成变轨，输出预期的结果值，具有燃料消耗次优的特点，降低了发射成本。

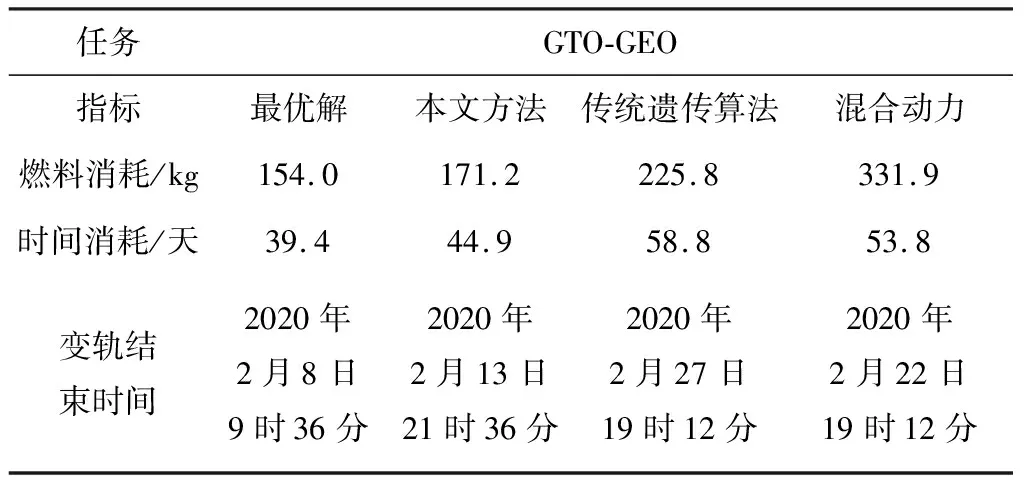
表4 GTO-GEO变轨燃料和时间消耗

5 结论

在连续小推力卫星变轨以及制导控制过程中，本文将电推进式小推力卫星模型的变轨过程转化为最优控制中两点边值问题，然后针对该问题使用混合遗传算法进行解算。在SCILAB6.0.1上进行实验，验证了本文提出的小推力卫星变轨算法优化设计方法。实验结果表明，变轨实际消耗燃料较最优解仅多1.2%，消耗时间较最优解仅多13.9%，且相较于传统遗传算法以及传统动力模型，燃料和时间消耗都大大减少，完成了小推力航天器由低轨向高轨的飞行轨道规划及优化。