带壁厚偏差管大变形推压缩径端部周向褶皱研究

2021-11-18王连东谭启莹王晓迪宋希亮

中国机械工程 2021年21期

刘恒王连东谭启莹王晓迪宋希亮

1.燕山大学河北省特种运载装备重点实验室，秦皇岛，066004 2.燕山大学车辆与能源学院，秦皇岛，0660043.燕山大学机械工程学院，秦皇岛，066004

0 引言

推压缩径是指使管坯通过锥形凹模以减小其外径的冷成形加工方法[1]，具有模具结构简单、制造成本低、生产效率高等优势，已经广泛应用于汽车、工程机械及航空航天等工业领域的变径管件制造[2-3]。

目前关于管坯推压缩径的研究较多。彭俊阳等[4]进行了不同缩径系数的缩径实验，研究了缩径过程中壁厚及最大轴向力的变化规律。王连东等[5]分析了推压缩径管坯端部存在翘曲的原因，并研究了工艺参数对端部翘曲的影响规律。刘恒等[6]研究了自由推压缩径管坯残余应力分布，结果表明端部翘曲区存在剪应力，并且端部由内表面层到外表面层均为周向拉应力。

推压缩径时，缩径力过大会引起管坯传力区轴向失稳起皱。孙志超等[7]对管轴压失稳起皱的力学过程、影响因素及影响规律进行了研究，并给出了失稳判据。LIU等[8]采用有限元模拟研究了温度对传动轴热挤压缩径传力区轴向失稳的影响，并给出了轴向不失稳的最佳成形工艺参数。TENG等[9]通过有限元模拟和试验研究了凹模锥角对薄壁圆筒杯形件缩口起皱的影响，结果表明锥角越大，越容易起皱。刘超等[10]研究了壁厚偏差对推压-拉拔复合缩径传力区轴向起皱的影响规律，并给出了传力区不失稳的最大壁厚偏差。

与推压缩径不同，采用黏性或固体颗粒介质对薄壁管中部外压缩径时，管坯中部变形区内、外壁均存在周向失稳起皱现象。关于薄壁合金管外压缩径周向起皱失稳的研究较多，高铁军等[11]分析了薄壁圆筒外压缩径失稳起皱过程中几何形状和应力的变化规律，并分析了坯料端部约束条件对起皱的影响。ZHAO等[12]针对薄壁管件外压缩径失稳起皱进行了分析，研究了成形因素对薄壁管件外压缩径抗皱性能的影响。张鑫等[13]针对薄壁管材外压缩径，采用有限元模拟研究了屈曲模态和厚度不均缺陷对起皱失稳的影响。

近期在工程实践中发现无缝钢管在大变形推压缩径时端部内壁存在凹凸不平的周向褶皱现象，定径区周向褶皱不明显。端部周向褶皱严重影响制件质量，而关于推压缩径管坯端部周向褶皱的研究尚未见文献报道。

本文通过理论分析，揭示了推压缩径管坯端部周向褶皱的生成机理；通过试验和有限元模拟验证理论分析的正确性，并揭示出不平度、相对不平度的演变规律及工艺参数对其的影响规律；提出了减小端部周向褶皱的措施。

1 无缝钢管壁厚测量

大变形推压缩径工艺一般选用热轧无缝钢管，由于轧制芯棒跳动、磨损及钢管加热不均等，导致管坯存在不可避免的壁厚偏差缺陷[14-15]。以某载重6.5t胀压成形汽车桥壳选用热轧Q345B无缝钢管(GB/T 8162—2018)为研究对象，初始管坯长度L0=1340 mm、外径d0=219 mm、理论壁厚为7.5 mm。自初始管坯端部沿轴向等间距确定11个测量横截面，并画出周向线；再在管坯外表面以等角度15°的周向间隔画出轴向线，则周向线与轴向线的交点即为壁厚测量点，如图1所示。随机选取10根管坯，采用MT-160型超声波测厚仪测量壁厚，其中3根管坯部分横截面一半的壁厚测量结果见表1，另一半壁厚分布基本对称。初始情况下，横截面上最大、最小壁厚分别为tm0、tn0，平均壁厚为t0，壁厚最大偏差δ0=tm0-tn0，壁厚最大正偏差δm=tm0-t0，壁厚最大负偏差δn=tn0-t0。

图1 管坯壁厚测量示意图Fig.1 Diagram of tube blank wall thickness measurement

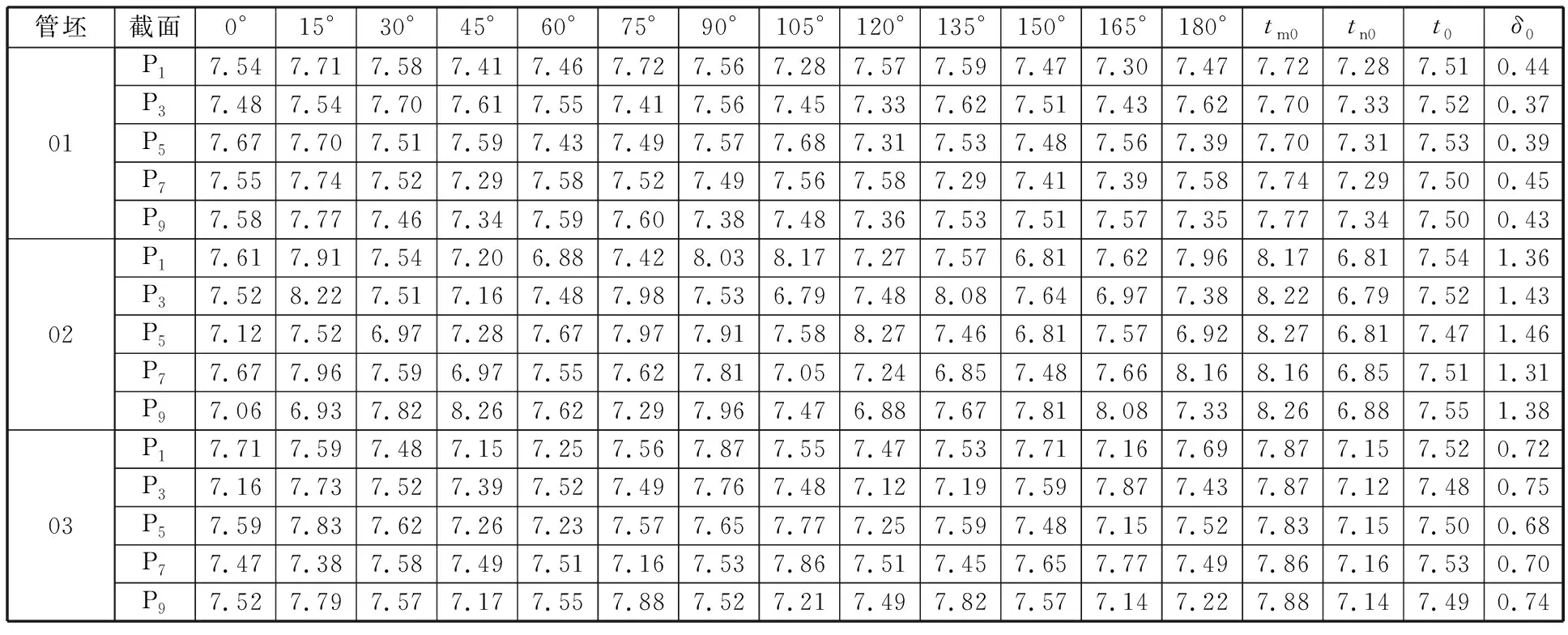
表1 初始管坯壁厚测量结果Tab.1 Results of initial tube blank wall thickness measurement mm

通过分析测量结果可发现：①管坯壁厚沿周向分布存在一定的薄厚交替性变化规律，如图2所示，01号管P1、P7横截面，02号管P3、P7横截面，03号管P5、P9横截面，自0°到180°壁厚大小均交替变化；②同一横截面壁厚最大正偏差δm与最大负偏差δn的绝对值较接近，01号管P1横截面δm=0.21 mm、δn=-0.23 mm，02号管P3横截面δm=0.70 mm、δn=-0.73 mm，03号管P5横截面δm=0.33 mm、δn=-0.35 mm。

图2 周向壁厚分布Fig.2 Circumferential wall thickness distribution

2 端部周向褶皱分析

管坯推压缩径时，上下夹持模固定管坯中部，缩径凹模由管坯端部向内侧缩径，缩径凹模型腔分为减径区、圆角区及出口区，见图3。

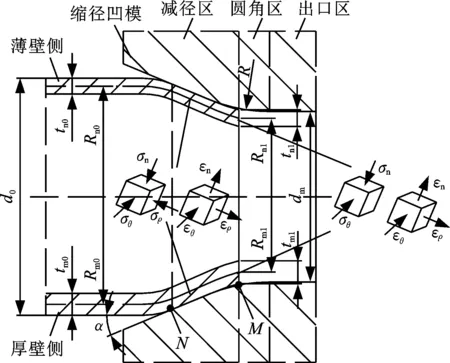
图3 减径阶段Fig.3 Diameter-reducing stage

将管坯横截面上最大壁厚tm与最小壁厚tn的差值定义为不平度δ，即

δ=tm-tn

(1)

将管坯不平度δ与平均内径di的比值定义为相对不平度η：

η=(tm-tn)/di

(2)

η作为是否产生周向褶皱的评价指标。

将国家标准所允许的无缝钢管最大壁厚偏差δx与其内径di0的比值作为临界相对不平度ηc：

ηc=δx/di0

(3)

当缩径后管坯相对不平度η大于临界相对不平度ηc时，即评价为产生周向褶皱。

由于初始管坯壁厚沿周向呈薄厚交替性变化，为便于分析，在建立带壁厚偏差的管坯推压缩径力学模型时，将管坯上侧定为壁厚较薄侧，下侧定为壁厚较厚侧，并假设初始管坯壁厚沿轴向不变，管坯外表面为圆柱面。

图3为带壁厚偏差管坯流经减径区的变形简图，缩径凹模的半锥角为α、出口处内径为dm、锥面与出口处的过渡圆角半径为R，减径阶段的起始与结束位置点分别为点N、M。管坯缩径前外径为d0，薄壁侧中间层半径为Rn0、壁厚为tn0，厚壁侧中间层半径为Rm0、壁厚为tm0，减径后薄壁侧中间层半径减至Rn1、壁厚增至tn1，厚壁侧中间层半径减至Rm1、壁厚增至tm1。

将管坯变形前后中间层半径比值的对数作为周向应变，则端部薄壁侧、厚壁侧在减径阶段的周向应变分别为

(4)

端部薄壁侧、厚壁侧在减径阶段的法向应变分别为

(5)

法向应变与周向应变的比值用λ表示，即

εn=λεθ

(6)

管坯减径的同时，壁厚增厚轴向伸长，周向压应变为主变形，使厚壁侧金属向邻近薄壁侧流动，有利于减小不平度。周向存在较大的压应力σθ，法向压应力σn较周向压应力σθ的数值很小；端部轴向应力σρ近似为零，端部内侧轴向应力为压应力，其数值大小由M点到N点逐渐增大。端部为自由端，由塑性变形关系可知端部法向应变比λ的绝对值近似为0.5，而端部内侧法向应变比λ的绝对值大于0.5，即当端部和定径区金属均减径变形到M点时，端部壁厚小于端部内侧。

端部经减径阶段变形后流入圆角区继续发生轴向弯曲变形，中间层外侧金属沿轴向缩短、厚度增厚，中间层内侧金属沿轴向伸长、厚度减薄，如图4a所示，薄壁侧中间层半径变为Rn2、壁厚变为tn2，厚壁侧中间层半径变为Rm2、壁厚变为tm2。在圆角变形区截取包含管坯内外表面的基元体，其轴向长度为单位1，周向角度为单位1，壁厚为te，如图4b所示。为便于分析，假设：管坯壁厚中间层与中性层重合；中间层外侧轴向压应力以等效应力σρe1作用于其厚度一半处，中间层内侧轴向拉应力以等效应力σρe2作用于其厚度一半处，且中间层内外侧等效轴向应力大小相等。

(a) 弯曲变形 (b) 圆角区基元体图4 圆角阶段Fig.4 Rounded corner stage

则基元体左侧面上的力矩dM为

(7)

假设在管坯同一横截面上，任意周向单位角度微面上中间层内外两侧的轴向应力对其形成的力矩大小均相等。由于存在壁厚偏差，则由式(7)可知，薄壁中间层内侧金属的轴向拉应力大于厚壁侧，则薄壁中间层内侧金属轴向变形大于厚壁侧，致使薄壁中间层内侧金属减薄大于厚壁中间层内侧，使端部内壁的不平度增大。

端部经圆角区流出后，由于中间层内侧金属轴向伸长大于外侧，存在剪切变形γ和剪应力τρn，端部内表面层到外表面层均为周向拉应力σθ[6]，端部发生翘曲变形，产生周向扩径，引起壁厚减薄。如图5a所示，薄壁侧中间层半径增至Rn3、壁厚减至tn3，厚壁侧中间层半径增至Rm3、壁厚减至tm3。在端部翘曲区截取包含管坯内外表面及右端面的基元体，其轴向长度为单位1，左侧面为厚壁侧、壁厚为tm3、周向拉应力为σθm，右侧面为薄壁侧、壁厚为tn3、周向拉应力为σθn，左侧面与右侧面的周向夹角为θ，如图5b所示。根据切线方向力的平衡条件，可得

(8)

(a) 出口变形 (b) 端部基元体图5 出口阶段Fig.5 Exit stage

由式(8)可知，薄壁侧周向拉应力大于厚壁侧，则薄壁侧周向变形大于厚壁侧，致使薄壁侧壁厚减薄大于厚壁侧，使端部不平度进一步增大，若相对不平度超过临界值即产生周向褶皱。而端部内侧金属在出口区不再发生翘曲变形，不平度亦不再变化，即形成管坯定径区。

3 推压缩径试验研究

3.1 试验方案

选用GB/T 8162—2018热轧Q345B无缝钢管，外径d0为219 mm、理论壁厚为7.5 mm。选取最大壁厚偏差δ0(即初始不平度)分别为0.4 mm、0.8 mm、1.2 mm的三根管坯，根据国家标准该规格管坯壁厚最大允许偏差为2.25 mm，则临界相对不平度ηc为1.10%。根据工程实践经验，将缩径后管件相对不平度位于1.10%～1.40%的评价为一般周向褶皱(即允许质量缺陷)，将相对不平度大于1.40%的评价为严重周向褶皱。

在THP63-200/300/100×2型专用缩径液压机上分别进行四道次推压缩径，缩径时对管坯中部进行夹持，保持456 mm的长度区域不变形，如图6所示。各道次的缩径凹模内径及总缩径系数(管坯缩径后外径与初始管坯外径的比值)见表2。

(a) 初始管坯

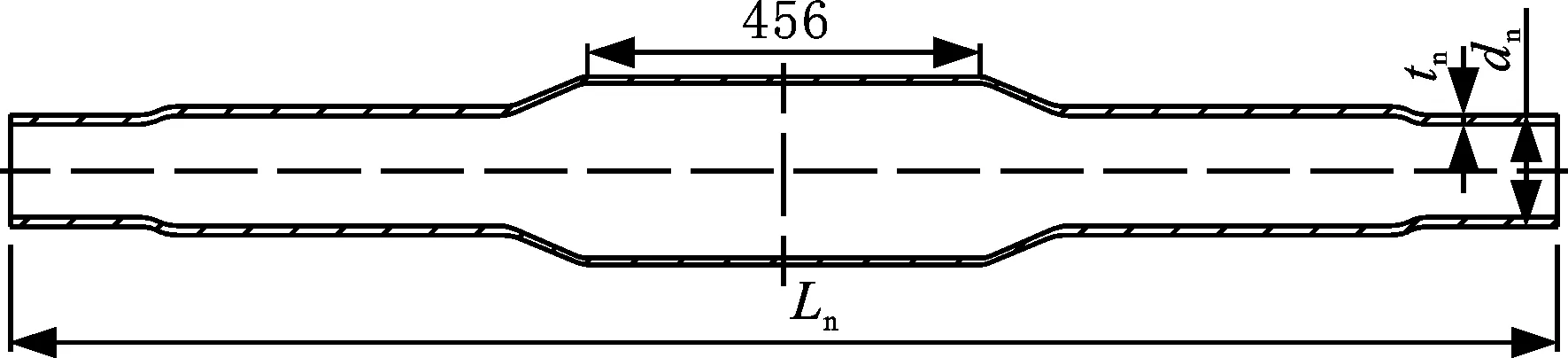
(b) 第四道次缩径管坯图6 缩径工艺示意图Fig.6 Process diagram of diameter-reducing

表2 四道次缩径参数Tab.2 Parameters of four times diameter-reducing

推压缩径模具如图7所示。进行不同道次推压缩径时，只需更换缩径凹模。缩径前将管坯两侧拟缩径区域外壁、缩径凹模内壁涂抹润滑油，将管坯放入下夹持模并进行中心对正定位；缩径时液压机主滑块带动上模座与上夹持模向下运动夹持管坯中部，液压机左右滑块分别带动左右缩径凹模由管坯两侧端部向内侧缩径。

1.左支撑筒 2.左缩径凹模 3.上模座 4.上夹持模 5.下夹持模 6.下模座 7.右缩径凹模 8.右支撑筒图7 推压缩径模具Fig.7 Die of pushing diameter-reducing

3.2 试验结果及分析

每道次缩径完成后，分别测量管坯端部最大与最小壁厚、端部翘曲量(端部与定径区半径的差值)，并在缩径管坯右侧距端部50 mm处沿横向剖切，测量定径区最大与最小壁厚。

如图8所示，缩径后管坯端部不平度δd分别为0.86 mm、1.51 mm、2.43 mm，凹凸波数分别为14、16、18，δ0=1.2 mm管坯端部内壁存在明显周向褶皱；定径区不平度δi分别为0.35 mm、0.61 mm、0.85 mm；各缩径管坯端部均存在翘曲，并且端部周向褶皱主要分布于翘曲区内壁，端部翘曲量分别为1.64 mm、1.66 mm、1.69 mm，翘曲区长度分别为23.35 mm、23.61 mm、23.82 mm。

(a) δ0=0.4 mm端部 (b) δ0=0.8 mm端部

取最大壁厚与最小壁厚的均值为平均壁厚，则各道次缩径管坯端部及定径区平均壁厚见表3，可以看出端部平均壁厚td均小于定径区平均壁厚ti，与理论分析吻合。

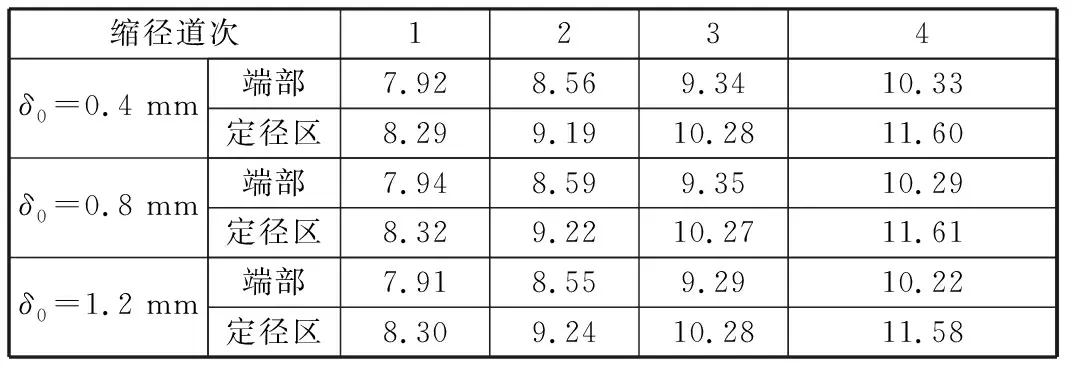
表3 缩径管坯平均壁厚Tab.3 Average wall thickness of diameter-reducing tube mm

不同δ0管坯四道次缩径后不平度如图9a所示，端部不平度δd大于初始不平度δ0，定径区不平度δi均小于初始不平度δ0；随着壁厚偏差增大、缩径道次增大(即减径变形量增大)，端部不平度δd急剧增大，定径区不平度δi缓慢增大。δ0=0.4 mm、δ0=0.8 mm和δ0=1.2 mm管坯四道次缩径后端部δd分别为0.86 mm、1.51 mm、2.43 mm，定径区δi分别为0.35 mm、0.61 mm、0.85 mm。

由图9b可知，随着壁厚偏差增大、缩径道次增加，端部相对不平度ηd急剧增大。δ0=0.4 mm管坯四道次缩径端部均没有周向褶皱；δ0=0.8 mm管坯第4道次缩径端部产生严重褶皱；δ0=1.2 mm管坯第2道次缩径端部产生一般褶皱，第3和第4道次缩径端部均产生严重褶皱。

(a) 不平度

(b) 相对不平度图9 试验不平度与相对不平度Fig.9 Unevenness and relative unevenness of the tests

4 周向褶皱模拟研究

4.1 管坯材料属性

根据GB/T 228.1—2010标准制取比例拉伸试样，在初始管坯和前3道次缩径管坯定径区的中部，沿轴向进行线切割，发现除初始管坯的试样外，各道次缩径管坯试样的两夹持端均存在向上翘曲现象。将拉伸试样两夹持端压平，室温条件下，在Inspekt-Table100型电子万能试验机上进行单向拉伸试验，得到初始管坯和各缩径管坯的应力-应变曲线，并采用幂函数形式拟合得到应力-应变关系，如图10所示。

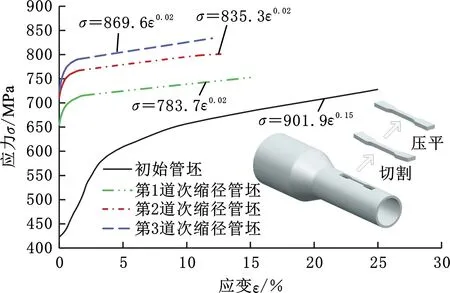
图10 应力-应变关系曲线Fig.10 Stress-strain curve

由单向拉伸试验结果可以发现，各道次缩径管坯的屈服强度和抗拉强度均明显高于初始管坯，并且随着缩径道次增加，管坯的屈服强度和抗拉强度均增大。各道次缩径管坯的延伸率和断面收缩率见表4，可以看出随着缩径道次增加，管坯的延伸率和断面收缩率均逐渐降低，即缩径管坯的塑性变形能力随缩径道次的增加而逐渐变差，可能产生开裂现象。

4.2 壁厚偏差管几何模型及缩径有限元模型

基于无缝钢管壁厚测量结果，做出以下假设：①管坯外表面形状为圆形，内表面形状为周期性变化的正弦曲线；②同一横截面上的壁厚最大正偏差δm与最大负偏差δn的绝对值相等；③同一轴线上的壁厚相同。

根据上述假设，建立内表面为周期性正弦变化的壁厚偏差管坯几何模型，如图11所示。内壁正弦曲线的波谷即为最小壁厚tn0，波峰即为最大壁厚tm0；波幅即为δ0/2，周期角度为θn，波数为n。

图11 壁厚偏差管坯几何模型Fig.11 Geometrical model of tube with wall thickness deviation

分别建立δ0为0.4 mm、0.8 mm、1.2 mm、1.6 mm，d0为219 mm，t0为7.5 mm，波数n为15的壁厚偏差管坯几何模型，针对图6所示工艺，采用有限元软件ABAQUS进行四道次推压缩径模拟。由于初始管坯、缩径凹模均为轴对称结构，为便于计算分析，分别建立壁厚偏差管四道次推压缩径的1/4有限元模型，如图12所示。

图12 有限元模型Fig.12 Finite element model

在管坯纵向中心截面和中间横截面上分别设置对称约束；采用上下夹持模固定管坯中部，各道次缩径凹模、夹持模均设定为刚体，管坯设定为变形体，管坯网格类型采用六面体单元C3D8R。采用库仑摩擦模型，夹持模与管坯间建立刚-柔接触，其接触动摩擦因数设定为0.15；各缩径凹模与管坯间建立刚-柔接触，其接触动摩擦因数设定为0.10。

4.3 周向褶皱产生与发展过程

4.3.1δ0=1.2mm管坯第1道次缩径变形过程

图13所示为δ0=1.2 mm管坯第1道次缩径变形过程，管坯上侧为最小壁厚的波谷侧，下侧为最大壁厚的波峰侧。在端部波谷侧、波峰侧的内外表面分别选取测量点B、A、E、F；在距端部25 mm的端部内侧波谷侧、波峰侧内外表面分别选取测量点D、C、G、H。

(a) 缩径前管坯

(b) 减径阶段

(d) 出口阶段图13 δ0=1.2 mm管坯第1道次缩径变形周向应力云图Fig.13 Cloud chart of circumferential stress of the 1st tube diameter-reducing deformation with δ0=1.2 mm

(1)减径阶段。在减径区，各测量点周向应力σθ和法向应力σn均为压应力。端部完成减径阶段变形时，外径减至183.91 mm，最大法向压应力数值为C点的83.67 MPa，远小于该点的周向压应力值795.64 MPa；端部点A、B、E、F轴向应力大小均趋于零，点C、D、G、H轴向应力均为压应力，大小分别为452.29 MPa、468.34 MPa、495.15 MPa、519.36 MPa；端部波谷、波峰侧壁厚则分别增至7.47 mm、8.68 mm，不平度δd为1.21 mm，基本无变化。端部内侧完成减径阶段变形时，外径减至190.15 mm，波谷、波峰侧壁厚分别增至7.71 mm、8.62 mm，不平度δi减小至0.91 mm。

(2)圆角阶段。由于端部经减径区变形后外径较小，在端部完成圆角阶段变形时，外径增大至188.08 mm，点A、B、E、F周向应力为拉应力，大小分别为635.91 MPa、618.78 MPa、621.97 MPa、642.41 MPa；外表面层点C、H轴向应力为压应力，大小分别为447.47 MPa、415.05 MPa，内表面层点D、G轴向应力为拉应力，大小分别为449.50 MPa、406.51 MPa，与理论分析相吻合。端部波谷、波峰侧壁厚分别减薄至7.36 mm、8.65 mm，波谷侧减薄量远大于波峰侧，不平度δd增大至1.29 mm。端部内侧完成圆角阶段变形时，外径减小至187.82 mm，波谷、波峰侧壁厚分别增厚至7.93 mm、8.69 mm，不平度δi减小至0.76 mm。

(3)出口阶段。端部在出口区继续发生翘曲变形，端部外径扩径至190.21 mm，点A、B、E、F周向拉应力大小分别为642.31 MPa、619.21 MPa、607.49 MPa、640.57 MPa，端部翘曲区由外表面到内表面均存在剪应力τρn，其中波谷、波峰侧最大剪应力大小分别为86.82 MPa、84.46 MPa；波谷、波峰侧壁厚分别减薄至7.27 mm、8.61 mm，波谷侧减薄量远大于波峰侧，且不平度δd进一步增大至1.34 mm。而端部内侧在出口区不再发生翘曲变形，不平度δi亦不再变化。有限元模拟结果与理论分析相吻合。

4.3.2δ0=1.2mm管坯多道次缩径结果

δ0=1.2 mm管坯第2、第3、第4道次缩径结果如图14所示。可以看出，随着缩径道次增加即缩径变形量增大，端部不平度δd明显增大，与试验结果趋势吻合。

(a) 第2道次缩径

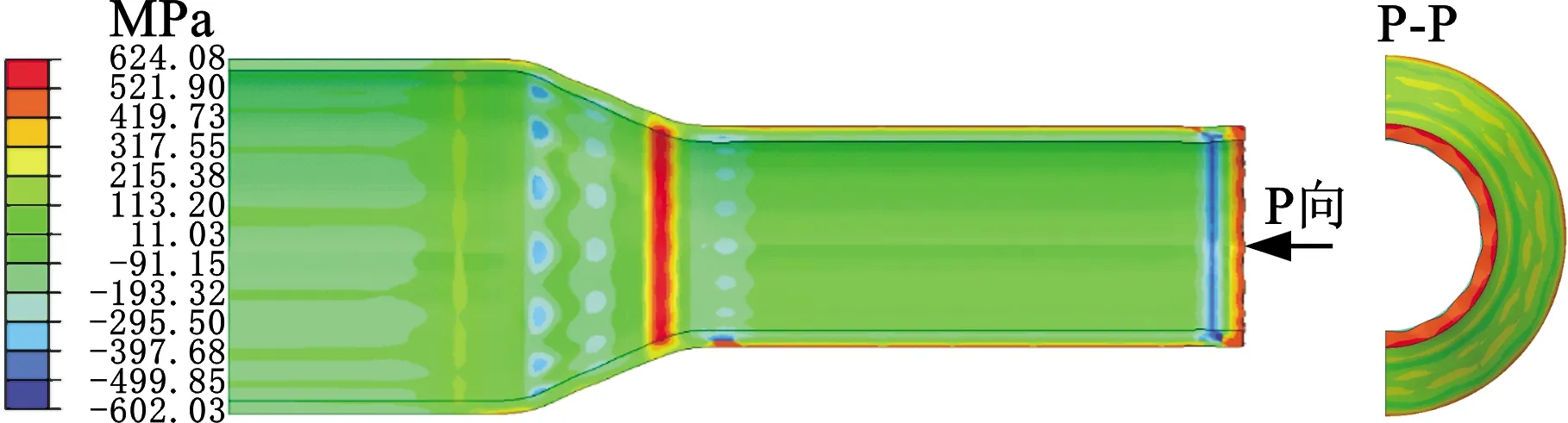
(b) 第3道次缩径

各道次缩径管坯端部不平度δd分别为1.62 mm、1.79 mm、2.20 mm，定径区不平度δi分别为0.75 mm、0.87 mm、0.96 mm；端部相对不平度ηd分别为1.12%、1.55%、2.33%，即第2道次缩径端部产生一般褶皱、第3和第4道次缩径端部均产生严重褶皱。端部周向褶皱主要位于翘曲区内，翘曲量分别为1.70 mm、1.78 mm、1.79 mm，翘曲长度分别为23.73 mm、23.80 mm、23.87 mm。

4.4 不同δ0管坯缩径模拟结果分析

4.4.1管坯缩径壁厚变化规律

不同δ0管坯第1道次缩径各变形阶段端部和端部内侧的壁厚变化如图15所示。可以看出，在减径阶段，端部波谷侧与波峰侧均发生增厚，自圆角阶段到出口阶段，端部波谷侧发生明显减薄，波峰侧减薄量较小；端部内侧自减径阶段到圆角阶段，波谷侧与波峰侧均发生增厚，且波谷侧增厚显著，而在出口阶段，波谷侧、波峰侧壁厚均不再发生变化；管坯缩径完成时，端部壁厚均小于定径区壁厚。

图15 壁厚变化过程Fig.15 Wall thickness change process

4.4.2管坯缩径相对不平度演变规律

不同δ0管坯第1道次缩径各变形阶段的端部和端部内侧相对不平度变化如图16所示。可以看出，端部相对不平度ηd和端部内侧相对不平度ηi均小于临界相对不平度ηc，端部相对不平度ηd自减径阶段到出口阶段均逐渐增大，而端部内侧相对不平度ηi自减径阶段到圆角阶段均逐渐减小，在出口阶段相对不平度ηi不再变化。

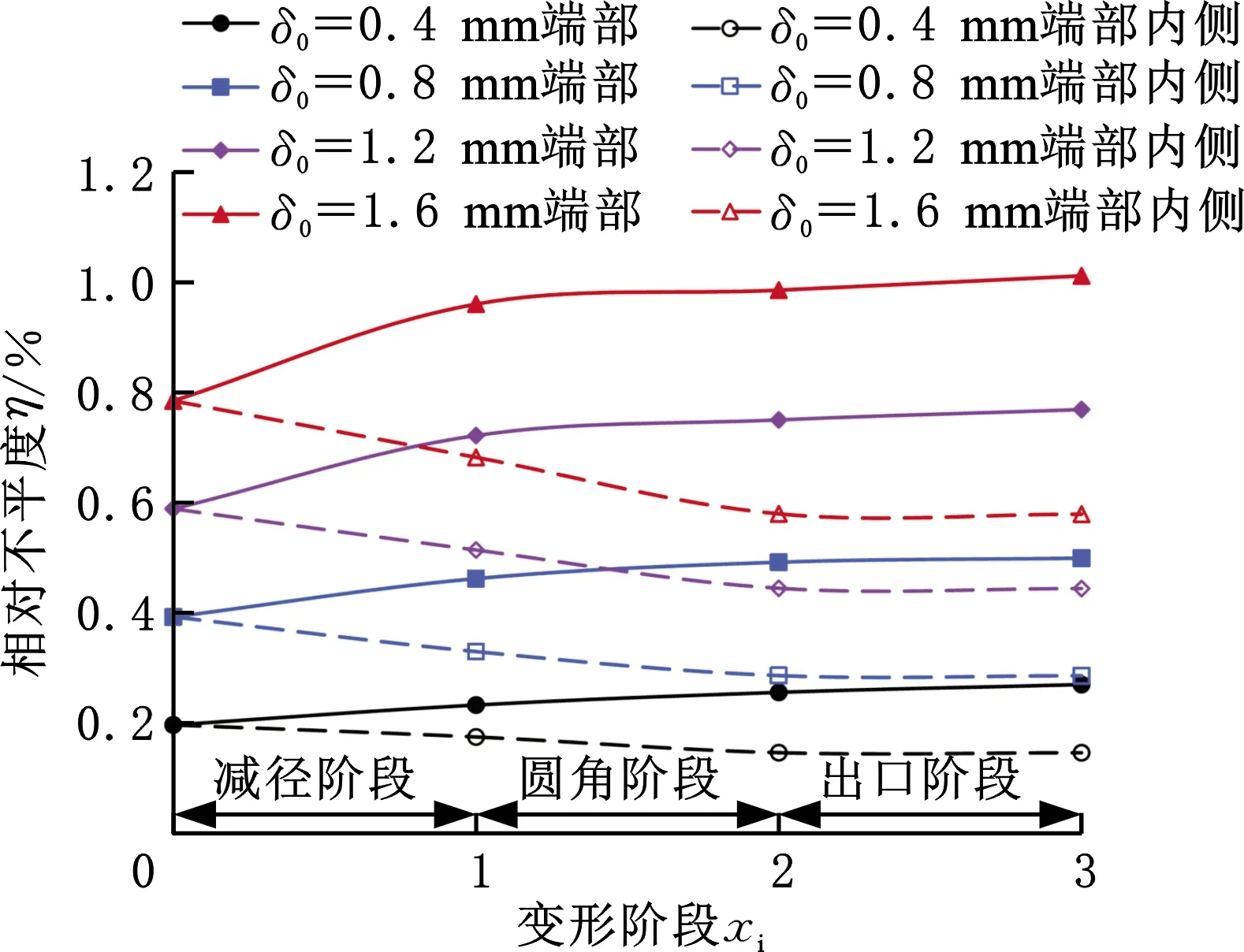
图16 相对不平度演变过程Fig.16 Relative unevenness evolution process

4.4.3工艺参数对不平度影响规律

不同δ0管坯缩径后不平度如图17a所示，可以看出，端部不平度δd均大于初始不平度δ0，定径区不平度δi均小于δ0；随着壁厚偏差增大、缩径道次增加，端部不平度δd急剧增大，定径区不平度δi缓慢增大。δ0=0.4 mm与δ0=1.6 mm管坯四道次缩径后端部不平度δd分别为0.78 mm、2.76 mm，定径区不平度δi分别为0.39 mm、1.48 mm。

由图17b可知，随着壁厚偏差增大、缩径道次增加，端部相对不平度ηd急剧增大。δ0=0.4 mm管坯四道次缩径端部均没有周向褶皱，δ0=1.6 mm管坯第2、第3和第4道次缩径端部均产生严重周向褶皱。

(a) 不平度δ

(b) 端部相对不平度ηd图17 不平度模拟与试验结果对比Fig.17 Comparison of unevenness between simulation and test results

对比不平度与相对不平度的模拟值与试验值可以看出，模拟与试验结果的趋势一致，但数值大小存在一定偏差。端部不平度、相对不平度的模拟值较试验值最大相差11.38%和11.22%，均为δ0=0.8 mm管坯第1道次缩径；定径区不平度最大相差12.94%，为δ0=1.2 mm管坯第4道次缩径。差值主要是由于有限元模型的管坯壁厚偏差分布、边界条件设置等与实际试验条件存在一定差别，并且试验测量也存在一定误差，但整体结果可靠，验证了所建立壁厚偏差管几何模型及有限元模拟结果的可靠性。

5 周向褶皱调控

5.1 调控方法

针对壁厚偏差较大的管坯，采用推压-拉拔缩径，在管坯内部施加芯轴，并在缩径凹模工进减径的同时向外拉动芯轴，在缩径凹模和芯轴的共同挤压作用下使端部不平度δd减小。图18为推压-拉拔缩径示意图，芯轴外径为dn，缩径前将芯轴推入管坯内部，当缩径凹模在推力Fs1的作用下以速度v0由管坯外端向内缩径的同时，芯轴在拉力Fm拉动下以速度vm由管坯内部向外端运动，且芯轴外拉速度vm大于凹模运动速度v0。

图18 管坯推压-拉拔缩径Fig.18 Pushing-pulling diameter-reducing

5.2 推压-拉拔缩径有限元模拟及结果分析

针对δ0=1.2 mm管坯采用有限元软件ABAQUS进行四道次推压-拉拔缩径模拟分析，基于管坯传力区轴向不失稳[16]，确定各道次芯轴外径分别为173.8 mm、144.8 mm、118.6 mm、93.7 mm。推压-拉拔缩径有限元模型如图19所示，管坯、夹持模与缩径凹模的设定与推压缩径有限元模型相同，将芯轴设定为刚体，芯轴与管坯间摩擦因数设定为0.15，凹模工进速度为10 mm/s，芯轴外拉速度为12 mm/s。

图19 推压-拉拔缩径有限元模型Fig.19 Finite element model of pushing-pulling diameter-reducing

δ0=1.2 mm管坯推压-拉拔缩径模拟结果如图20所示，可以看出，推压-拉拔缩径管坯端部无明显周向褶皱和翘曲。

(a) 第1道次缩径

(b) 第4道次缩径图20 δ0=1.2 mm管坯推压-拉拔缩径模拟周向应力云图Fig.20 Cloud chart of circumferential stress of tube pushing-pulling diameter-reducing with δ0=1.2 mm

各道次缩径管坯端部不平度δd分别为0.42 mm、0.29 mm、0.31 mm、0.33 mm，均小于推压缩径的1.34 mm、1.62 mm、1.79 mm、2.20 mm；端部相对不平度ηd分别为0.24%、0.20%、0.26%、0.35%，均小于推压缩径的0.77%、1.12%、1.55%、2.33%；端部翘曲量分别为0.16 mm、0.18 mm、0.17 mm、0.18 mm，较推压缩径的1.69 mm、1.70 mm、1.78 mm、1.79 mm大幅减小。

5.3 试验验证

选取δ0=1.2 mm管坯在THP63-200/300/100×2型专用缩径液压机上进行四道次推压-拉拔缩径试验，各道次缩径凹模与推压缩径相同，各道次芯轴外径大小与有限元模拟值相同，如图21所示。

(a) 第一道次芯轴 (b) 第二道次芯轴

每道次缩径前，将芯轴置入管坯内部，在缩径凹模以10 mm/s的速度工进缩径的同时，以12 mm/s的速度外拉芯轴，缩径后管坯如图22所示，为便于测量观察，将第4道次缩径后管坯沿1/4纵截面剖开。可以看出，各道次缩径管坯均没有周向褶皱，且第1道次缩径管坯内壁沿周向存在交替间隔的光亮处，即厚壁处受凹模与芯轴的挤压作用显著，使厚壁处金属向邻近薄壁处流动。

(a) 第1道次缩径管坯

(b) 第4道次缩径管坯图22 推压-拉拔缩径管坯Fig.22 Pushing-pulling diameter-reducing tube

各道次推压-拉拔缩径与推压缩径管坯端部翘曲、不平度与相对不平度对比结果见表5。对比结果表明：①推压-拉拔缩径可以有效降低端部不平度和相对不平度，各道次缩径管坯端部不平度δd较推压缩径分别减小了52.82%、69.46%、74.48%、80.25%，端部相对不平度ηd明显减小，且均小于初始相对不平度0.59%和临界相对不平度1.10%，有效控制了端部周向褶皱；②推压-拉拔缩径可以大幅减小端部翘曲，各道次缩径管坯端部翘曲量较推压缩径分别减小了70.91%、80.86%、84.15%、86.98%，缩径后管坯成形质量较好。模拟与试验结论相吻合。

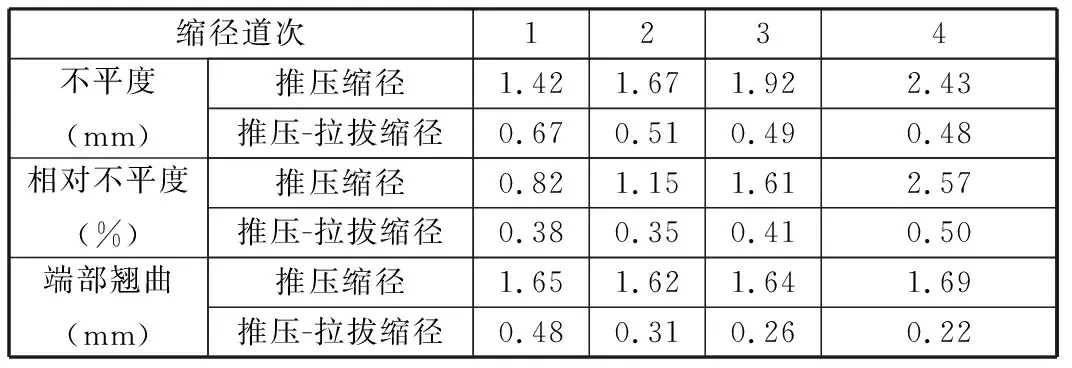
表5 试验结果对比Tab.5 Comparison of test results

6 结论

(1)本文通过建立带壁厚偏差管坯的推压缩径力学模型，分析了管坯薄壁侧、厚壁侧在减径区、圆角区及出口区的应力应变状态及变形特征，揭示出端部、端部内侧不平度的变化趋势以及端部翘曲区内壁周向褶皱的生成机理。

(2)通过测量无缝钢管壁厚，发现壁厚沿周向分布存在薄厚交替性变化规律。进行不同壁厚偏差管四道次推压缩径试验，结果表明：端部不平度均大于初始不平度，定径区不平度均小于初始不平度；随着壁厚偏差增大、缩径道次增加，定径区不平度缓慢增大，而端部不平度、相对不平度均急剧增大；试验结果与理论分析吻合，并给出了产生周向褶皱的工艺参数范围，且周向褶皱主要位于端部翘曲区内壁。

(3)基于无缝钢管壁厚测量结果，建立了内表面为周期性正弦变化的壁厚偏差管几何模型；模拟出了端部周向褶皱的产生与发展过程，分析了缩径各阶段应力与变形，揭示出壁厚、相对不平度的演变规律，与理论分析吻合；并揭示出壁厚偏差和缩径道次对不平度和相对不平度的影响规律，与试验结果趋势一致。

(4)针对δ0=1.2 mm管坯进行四道次推压-拉拔缩径有限元模拟和试验验证，结果表明：与推压缩径相比，端部翘曲明显减小，端部不平度、相对不平度大幅减小，有效提高了成形质量。