工序尺寸换算中虚公差的产生原因及处理方法
2021-11-18冯文慧马晓三
冯文慧 马晓三
(1.黄河交通学院机电工程学院,河南 焦作 454950;2.焦作市物料输送设备关键件制造工艺与装备工程技术研究中心,河南 焦作 454950;3.河南理工大学机械与动力工程学院,河南 焦作 454000)
在偏心型食品搅拌机机架、搅拌器[1]等具有复杂结构的机械零件加工工艺规程编制过程中,当工艺基准与设计基准不重合时,在确定工序余量之后,需通过工艺尺寸链对工序尺寸及其极限偏差进行换算。在工艺尺寸链计算过程中,有时候会出现换算出的工序尺寸上极限偏差小于下极限偏差的情况,即工序尺寸公差值为负值,这种尺寸公差被称为虚公差[2]。在工程实践中,工序尺寸虚公差的出现将导致工艺规程无法指导零件的加工和检验。因此,对工序尺寸虚公差产生的原因进行分析,并且在工艺尺寸链计算过程中,对有关尺寸采取有针对性的处理措施,避免工序尺寸虚公差的产生,对于保证机械加工工艺规程在生产现场的可执行性是十分必要的。
目前,有中国学者[2-6]围绕虚公差的基础理论及其在装配尺寸链中的应用展开了大量研究,并得到了国际学界的关注和认可。2016年9月,在第41届ISO/TC213年会上,专门就虚公差理论及应用进行了主题为《Chinese input on potential new work on virtual tolerances》的研讨[3]。而对于机械加工中工序尺寸虚公差现象,目前尚未有研究成果见诸报道。
基于以上情况,文章拟通过分析工序尺寸换算中工艺尺寸链极值计算法的原理和特点,对工序尺寸虚公差产生的原因进行研究,并以工艺尺寸链中各组成环尺寸之间的误差补偿关系为基础,从封闭环的选择、已知组成环尺寸公差的合理压缩以及根据其他组成环尺寸的实际偏差确定工序尺寸公差3方面,提出工艺尺寸链处理和改进方法,以期为解决工程实践中的工序尺寸虚公差问题提供理论依据。
1 工序尺寸虚公差产生原因
1.1 虚公差产生原因理论分析
在零件工艺基准与设计基准不重合的情况下,利用工艺尺寸链对加工工序尺寸进行计算的目的就是通过合理确定工序尺寸的基本尺寸H、上极限偏差ES(H)和下极限偏差EI(H),间接保证最终设计尺寸满足设计图要求。工序尺寸在设计图纸中不直接标出,但在工艺尺寸链中作为组成环,需要在加工中直接保证。工艺尺寸链的封闭环通常是在零件设计图纸中直接标出的设计尺寸,但需要在加工过程中间接保证[7-9]。工序尺寸换算过程中需要对工艺尺寸链极值法反计算[10],求出工序尺寸及其极限偏差。因为在尺寸链的计算中,封闭环尺寸的公差等于所有组成环尺寸的公差之和,所以工艺尺寸链中各尺寸的公差满足以下关系:
T(H)=T(M∑)-∑T(M),
(1)
式中:
T(H)——工序尺寸的公差;
T(M∑)——封闭环设计尺寸的公差;
∑T(M)——工艺尺寸链中除工序尺寸之外的其他所有组成环尺寸(即已知组成环尺寸)的公差之和。
从式(1)可以看出,当工艺尺寸链中的封闭环尺寸的公差小于已知组成环尺寸的公差之和时,封闭环的公差不足以向作为其中一个组成环的工序尺寸分配,就会出现工序尺寸的公差为负值,即虚公差的情况。
1.2 虚公差产生原因实例分析
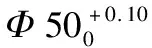
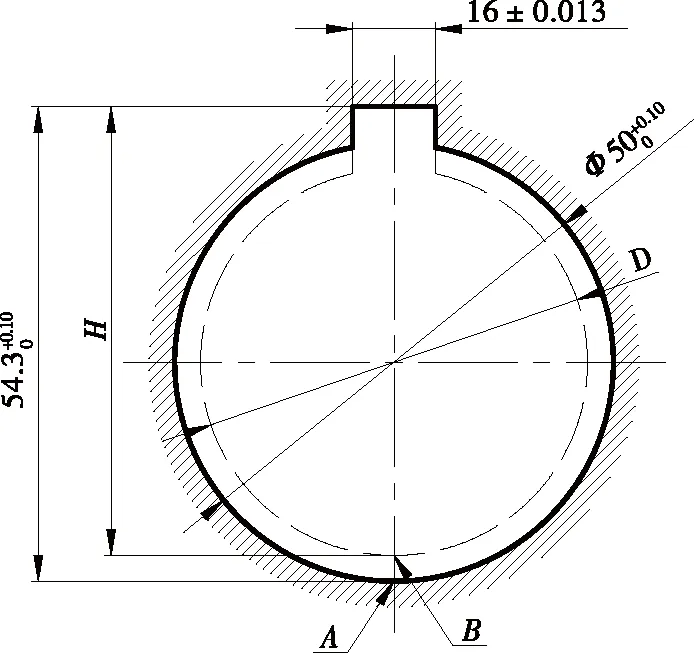
图1 某零件内孔及键槽设计尺寸和工序尺寸示意图
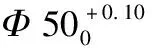
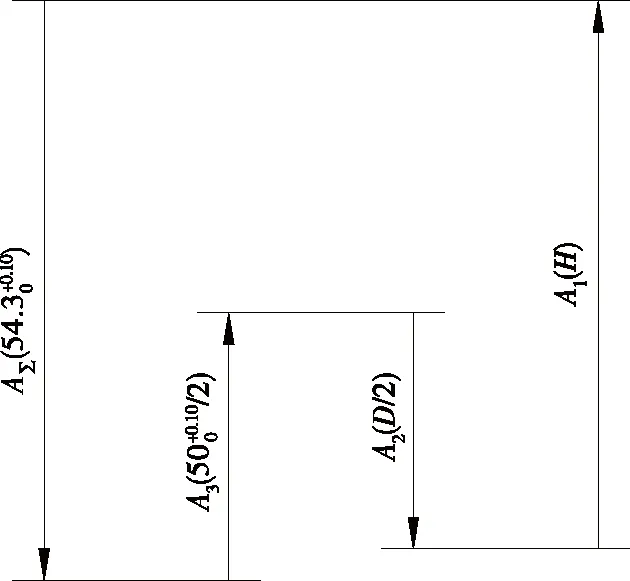
图2 某零件加工内孔及键槽工艺尺寸链示意图
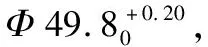
将以上各尺寸的公差代入式(1),可得工序尺寸H的公差:
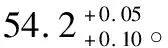
2 避免工序尺寸虚公差的工艺尺寸链处理方法
如前所述,在尺寸链的计算中,封闭环尺寸的公差为所有组成环尺寸的公差之和。因此,避免工序尺寸换算过程中产生虚公差,就是在建立和计算工艺尺寸链过程中,避免已知组成环尺寸的公差之和大于封闭环公差。具体而言,需从以下3方面对工艺尺寸链采取处理措施。
2.1 合理选择工艺尺寸链的封闭环
在采用极值法对尺寸链计算过程中,封闭环的公差是所有组成环的公差之和,封闭环一定是尺寸链所有尺寸中公差最大的。因此在建立工艺尺寸链时,封闭环的公差应尽可能大,必须将加工最后形成的尺寸中公差最大的作为封闭环进行间接保证。否则,除工序尺寸之外的其他所有组成环的公差之和大于封闭环公差的情况将不可避免,并出现虚公差。
2.2 合理压缩工艺尺寸链中已知组成环尺寸公差
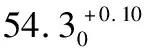
因此,在工序尺寸换算过程中,工艺尺寸链建立后,必须验证封闭环尺寸是否满足大于已知组成环尺寸公差之和的条件,如果不满足,则需通过合理压缩各个组成环尺寸的公差的方法满足该条件。在此过程中,从以下方面注意公差压缩处理的合理性。
(1)当已知组成环尺寸的基本尺寸与原公差带的中心值不重合时,应将其公差向原公差带的中心值附近压缩,而不能向基本尺寸附近压缩,避免加工后的零件尺寸相对于设计尺寸出现系统性误差[13-14]。
(2)尺寸公差与零件的加工工艺性直接相关,因此工艺尺寸链中各已知组成环尺寸的公差并非压缩得越小越好。对已知组成环尺寸公差压缩过程中,应结合形成各尺寸的工序的加工特点和实际情况,综合考虑零件加工工艺性。
2.3 根据工艺尺寸链其他组成环实际尺寸确定工序尺寸公差
在工程实践中,对工艺尺寸链中已知组成环尺寸公差的压缩,往往会提高零件的加工精度和加工难度。因此,由于零件加工工艺性和经济性限制,对工艺尺寸链已知组成环尺寸公差的压缩,并不能满足所有虚公差问题处理的需要。当工艺尺寸链已知组成环尺寸公差压缩至零件加工工艺性允许的极限,计算出的工序尺寸公差仍为负值时,可以在工艺尺寸链计算中用先于工序尺寸生成的组成环尺寸的实际偏差代替其上下极限偏差,从而避免虚公差现象的产生。
工序尺寸为加工过程中生成的尺寸,加工生成工序尺寸之前,在工艺尺寸链中属于组成环的部分尺寸可能已经生成,部分尺寸尚未生成。在零件加工过程中,当工序尺寸形成在比较靠后的工序中生成,即有较多工艺尺寸链组成环尺寸先于工序尺寸生成时,可根据先于工序尺寸生成的组成环尺寸加工实际数值,再结合封闭环设计尺寸的公差要求,确定工序尺寸公差。
将工艺尺寸链中所有增环分成在零件加工过程中先于工序尺寸生成的增环Mp1和在工序尺寸加工之后生成的增环Mp2,将工艺尺寸链中所有减环分成先于工序尺寸生成的减环Mq1和在工序尺寸加工之后生成的减环Mq2。对于Mp1和Mq1在工序尺寸加工之前已经生成,在计算工序尺寸公差时就不再考虑这些尺寸的上下极限偏差,而需要考虑尺寸的实际偏差[15]。在这种情况下,在每个零件的工艺尺寸链计算时,相当于将Mp1和Mq1的公差记为零,且根据工艺编制过程中工序安排先粗后精的原则[16],其设计公差要求比后续生成的尺寸Mp2和Mq2大,这样将大大降低计算出的工序尺寸为负值的可能性,从而有效避免工序尺寸虚公差的产生。
如果工序尺寸在工艺尺寸链中为增环,则对工艺尺寸链采用极值法计算得出的工序尺寸及其上下极限偏差计算公式:
H=M∑+(∑Mq1-∑MP1)+(∑Mq2-∑Mp2),
(2)
(3)
(4)
式中:
H——工序尺寸的基本尺寸;
ES(H)——工序尺寸的上极限偏差;
EI(H)——工序尺寸的下极限偏差;
M∑——封闭环设计尺寸;
ES(Mq2)、ES(Mq2)——后于工序尺寸生成的减环尺寸Mq2和减环尺寸Mp2的上极限偏差;
EI(Mq2)、EI(Mq2)——后于工序尺寸生成的减环尺寸Mq2和减环尺寸Mp2的下极限偏差。
同理可以得出工序尺寸在工艺尺寸链中为减环情况下,得出的工序尺寸及其上下极限偏差计算公式:
H=(∑Mp1-∑Mq1)+(∑Mp2-∑Mq2)-M∑,
(5)
(6)
(7)
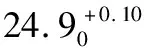
H=54.3+24.9-25=54.2 mm;
ES(H)=0.10+0.07-0.05=0.12 mm;
EI(H)=0+0.07-0=0.07 mm。
2.4 工序尺寸虚公差处理流程
综合以上所述,当工艺尺寸链虚公差现象发生后,可在工艺尺寸链建立和计算过程中,采取的改进和处理措施流程如图3所示。
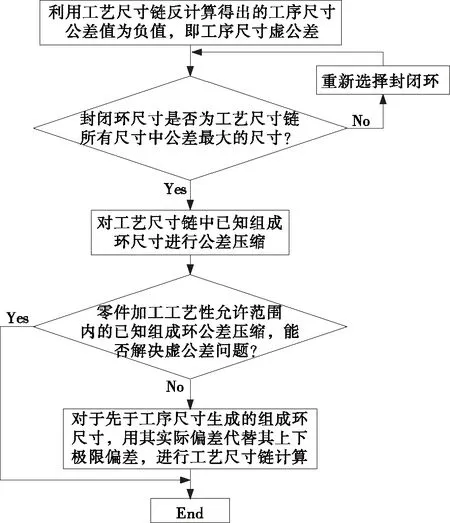
图3 针对工序尺寸虚公差现象的工艺尺寸链处理和改进流程
3 结论
工序尺寸虚公差是零件工艺基准和设计基准情况下,工艺尺寸链计算中的一种常见现象,而目前关于虚公差理论的研究,都是围绕装配尺寸链进行,对于零件机械加工工艺尺寸链计算中的工序尺寸虚公差问题的研究尚未开展。根据工艺尺寸链极值法计算的原理和特点,对工序尺寸虚公差产生的原因进行了分析,并从封闭环的选择、已知组成环尺寸公差的合理压缩以及根据先于工序尺寸形成的组成环尺寸的实际偏差确定工序尺寸公差3方面,提出了工艺尺寸链处理方法,避免工序尺寸虚公差现象的发生,并结合实例证明了上述原因分析的正确性和工艺尺寸链处理方法的可行性。相关研究方法和成果,为机械加工工艺编制过程中工序尺寸虚公差问题的处理提供了理论依据,同时为工序尺寸零公差或公差过小、工艺尺寸链中多个工序尺寸公差的分配等类似技术问题的处理提供了参考。
