基于卷积神经网络的白酒酒花分类研究

2021-11-18姚娅川

食品与机械 2021年10期

潘斌韩强姚娅川

(1.四川轻化工大学自动化与信息工程学院，四川自贡 643000；2.人工智能四川省重点实验室，四川自贡 643000；3.四川轻化工大学物理与电子工程学院，四川自贡 643000)

中国白酒生产工艺中摘酒是非常重要的环节，目前绝大数酒厂摘酒多由工人凭借经验按酒花进行分类，效率低下且分类不够客观、准确。为实现酒花自动分类，进一步实现自动化摘酒，国内外许多学者对代替人眼进行酒花分类开展了大量研究，赵平[1]设计了一种白酒量质摘酒过程中的图像采集和传输装置，避免了摘酒工需要进入生产车间，但仍然没有消除摘酒过程中的人工干预。何盛国等[2]在白酒蒸馏的甑罐出口设置了酒精度、风味物质在线检测仪器，完成分段摘酒。但该方法使用的在线检测仪器价格昂贵，难以实现大规模的自动化摘酒。范明明[3]利用近红外技术，开发了基于近红外技术的白酒摘酒在线检测装置，取得了较好的试验效果，但需要在白酒生产线上进行实用化试验。余锴鑫[4]提出了基于图像分类算法的自动化摘酒方法研究，将深度学习引入到白酒摘酒环节，但受到了计算量的限制，分类速度缓慢。陈林等[5]提出酒精度重建模型配合分段摘酒装置，通过音叉密度计建立基酒与酒精度模型的关系，来预测基酒酒精度。杨静娴等[6]提出基于图像处理的白酒酒花轮廓检测，采用模式识别的方式实现智能摘酒。

虽然目前已有酒企采用接触式设备进行智能摘酒，脱离了人工摘酒，但设备价格昂贵、维护成本高、不易实现大规模生产。而非接触式的机器视觉技术，因为成本低，方便快捷，易于大规模实现。研究拟提出基于卷积神经网络的酒花分类方法，以期实现智能摘酒。

1 酒花特征分析与数据集构建

1.1 酒花气泡特征分析

相同的温度和压强下，不同成分的酒会具有不同的黏度和表面张力，因此酒花会有所不同[7-8]。不同酒精度的基酒产生的酒花会不同即酒花与基酒酒精度有对应关系。酒花特征与酒精度的关系如表1所示。

表1 酒花特征与酒精度

1.2 酒花数据集构建

目前中国没有完整的酒花数据，需要人工采集，因此需要自行构建白酒酒花数据集。

1.2.1 工业相机选型工业相机具有高的成像质量、更快的传输速度、更好的图像稳定性和更强的抗干扰能力，考虑到图像传感器类型、分辨率、帧率、接口类型等，选择中国海康威视公司生产的MV-CA050-20GM/GC型工业面阵相机。其性能参数如表2所示。

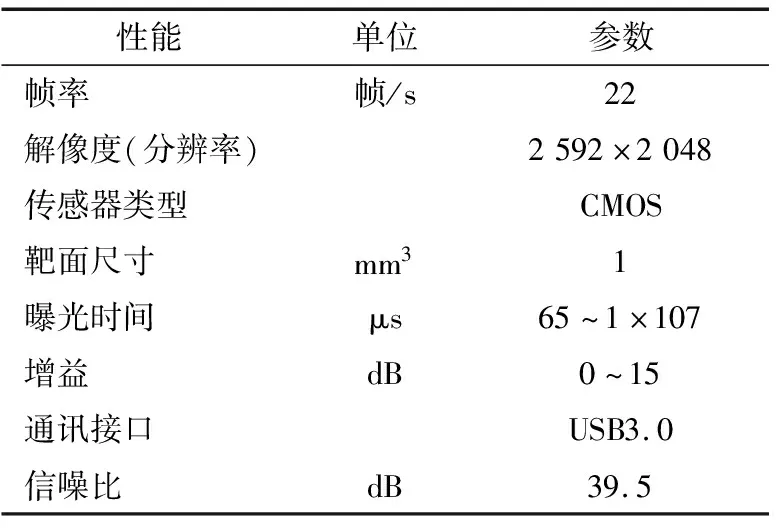
表2 MV-CA050-20型工业相机性能参数

1.2.2 数据采集为实现精确的酒花分类，采用控制变量法采集数据，利用蒸汽阀门控制流酒速度，盛酒器与流酒管高度固定。酒花数据来自中国某酒厂，采用MV-CA050-20GM/GC型工业面阵相机，由2名生产组组长协同采集(四段)酒花视频数据以保证样本的正确性。四段酒花数据包含不同角度、不同光照条件、不同摘酒现场的样本，基本考虑到了摘酒现场各种可能出现的因素。从四段酒花视频中分别逐帧提取头段酒花、中段酒花、末段酒花、酒尾酒花原始样本，分别获取1 375，1 386，1 369，1 386个样本，样本图像大小544×960×3，图像类型为JPG格式。

2 图像预处理

为了提高系统后续输入图像的可信度与分类准确率，减少分类时间，对图像进行预处理，包括：输入图像、图像灰度化、Gamam校正、图像滤波4步。

2.1 图像灰度化与Gamma 校正

图像灰度化是指将彩色图像中多个通道各种对应的分量通过一种方法转化为一个通道的灰度图[9]。文中选用加权平均法作为图像灰度化的方法，其数学表达式：

Gray=R×ωR+G×ωG+B×ωB，

(1)

式中：

R、G、B——对应通道的像素值；

ωR——R通道的权重，取0.299；

ωG——G通道的权重，取0.114；

ωR——B通道的权重，取0.587。

Gamma校正的压缩计算公式：

I(x,y)=I(x,y)g，

(2)

式中：

I(x,y)——灰度图；

g——校正值。

2.2 图像滤波

均值滤波是将滤波核内像素的平均值代替滤波核中心位置像素值[10]。假设现在使用3×3的模板对m×n的图像进形滤波，图解如图1所示。

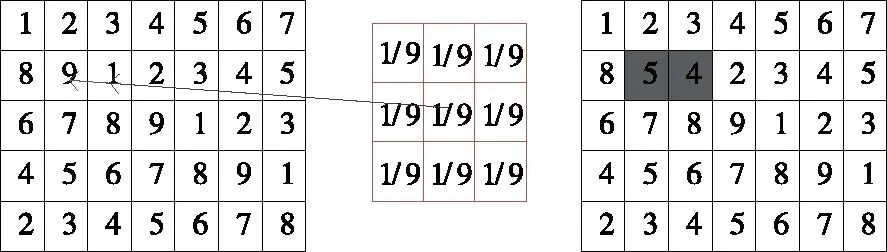
图1 均值滤波

由图2可知，均值滤波算法可表示为：

(3)

式中：

2≤x≤m-1;

2≤y≤n-1;

fa(x,y)——输出图像；

f(x,y)——原始图像；

m、n——图片大小。

中值滤波属于非线性滤波方法，基本思想是将滤波核的中心像素，由邻域像素灰度值的中值代替[11]，中值滤波示意如图2所示。

在图2中，采用3×3滤波核，滤波核的大小可以自己确定，常用滤波核大小有5×5，9×9形式，滤波核的大小通常为奇数。以3×3为例中值抑噪可由式(4)表示。

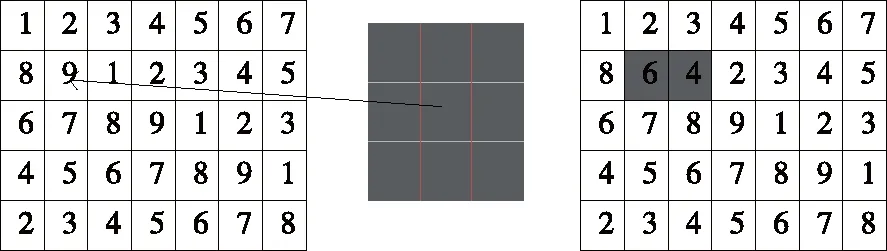
图2 中值滤波示意图

fm(x,y)=med[f(x+k,y+l)],(k,l∈[-1,1])，

(4)

式中：

f(x,y)——原始图像；

fm(x,y)——中值滤波后的结果图。

高斯滤波是一种线性平滑滤波，能为邻域内每个像素赋予权值，滤波核的中心像素由不同权值的邻域像素加权平均值确定[12]，高斯滤波图解如图3所示。

图3 高斯滤波

图3中高斯卷积核由二维高斯函数进行离散化得到，二维高斯函数如式(5)所示。

(5)

由式(5)离散化得到式(6):

(6)

式中：

k——核矩阵的维数；

σ——方差；

i、j——核矩阵中各点到中心点的距离。

以头段酒花为例各滤波示意图如图4所示。

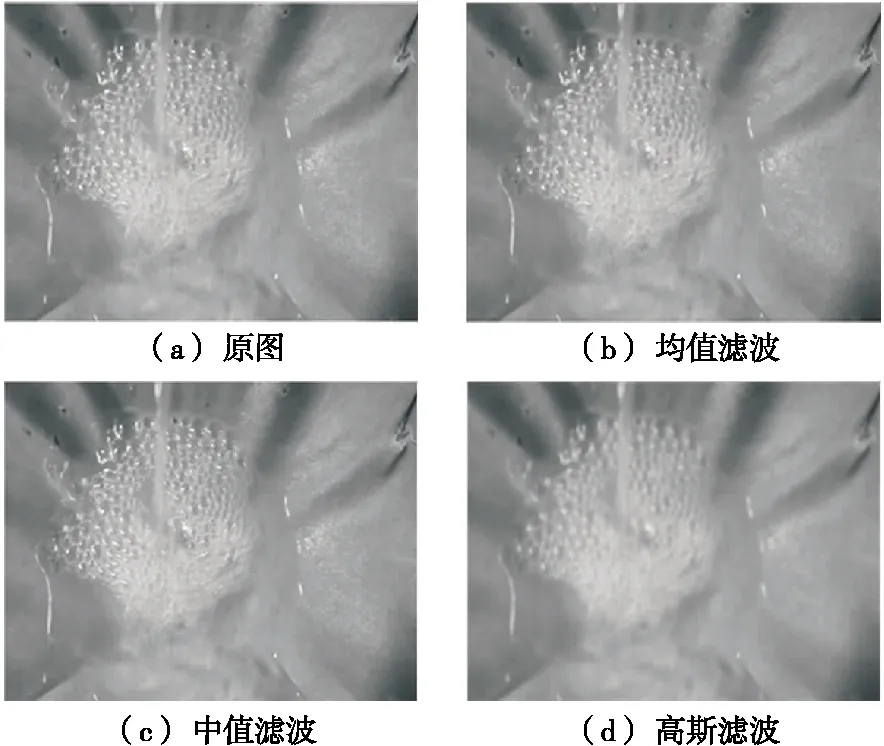
图4 滤波示意图

通过研究表明，白酒酒花图像中存在的噪声多为高斯噪声，因此选用高斯滤波。

3 基于卷积神经网络酒花分类模型设计

3.1 卷积神经网络

卷积神经网络是一种多层前馈神经网络，具备良好的自学习特征能力，强大的并行处理能力，以及优秀的鲁棒性，卷积网络的基本结构如图5所示。主要由输入层、卷积层、激活层和池化层、全连接层构成。

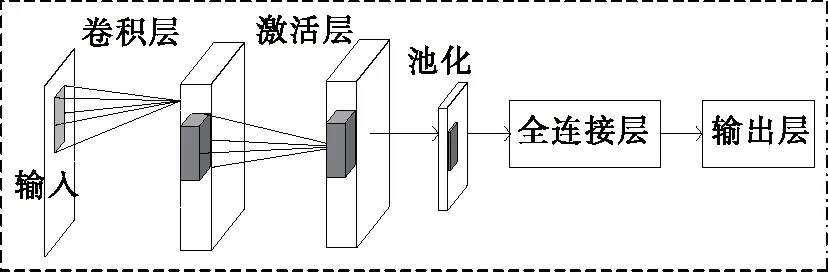
图5 卷积神经网络基本结构

(1)数据输入层：对待输入的样本图片进行一些预处理，例如将所有样本统一成相同的大小，方便后续的其他操作。

(2)卷积层：卷积层也叫特征提取层，是卷积神经网络的核心部分。卷积过程如图6所示。

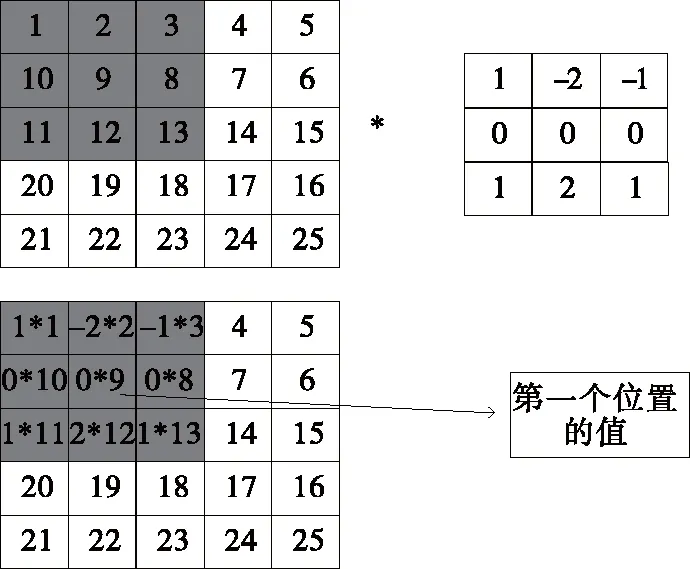
图6 卷积过程

(3)池化层：也被称为下采样层。池化就是对图像某个区域的特征进行统计分析，并将统计的结果用来表示整个区域的总体特征。运算过程如图7所示。

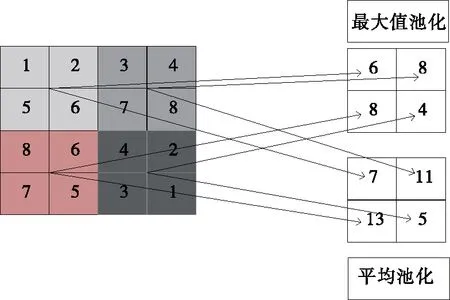
图7 池化过程

(4)激活层：解决线性模型所不能解决的问题，常见的激活函数有Sigmoid、Tanh、ReLU、PreLU、Maxout等。

(5)全连接层：将最后得到的图像特征，映射成一个固定长度的特征向量，传入分类器完成最终分类。

(6)输出层：输出层一般为分类器层，最后输出的是一个将制定分类的种类数目作为维度的概率向量。

3.2 基于改进Vgg16+迁移学习的模型设计

3.2.1 Vgg16模型传统Vgg16模型结构如表3所示，Vgg16总网络深度为16，其中包含13个卷积层和3个全连接层。输入图片大小为224×224×3的彩色图片，其卷积核采用随机初始化，池化层采用最大池化，激活函数采用ReLU激活函数，分类器采用Soft_max。

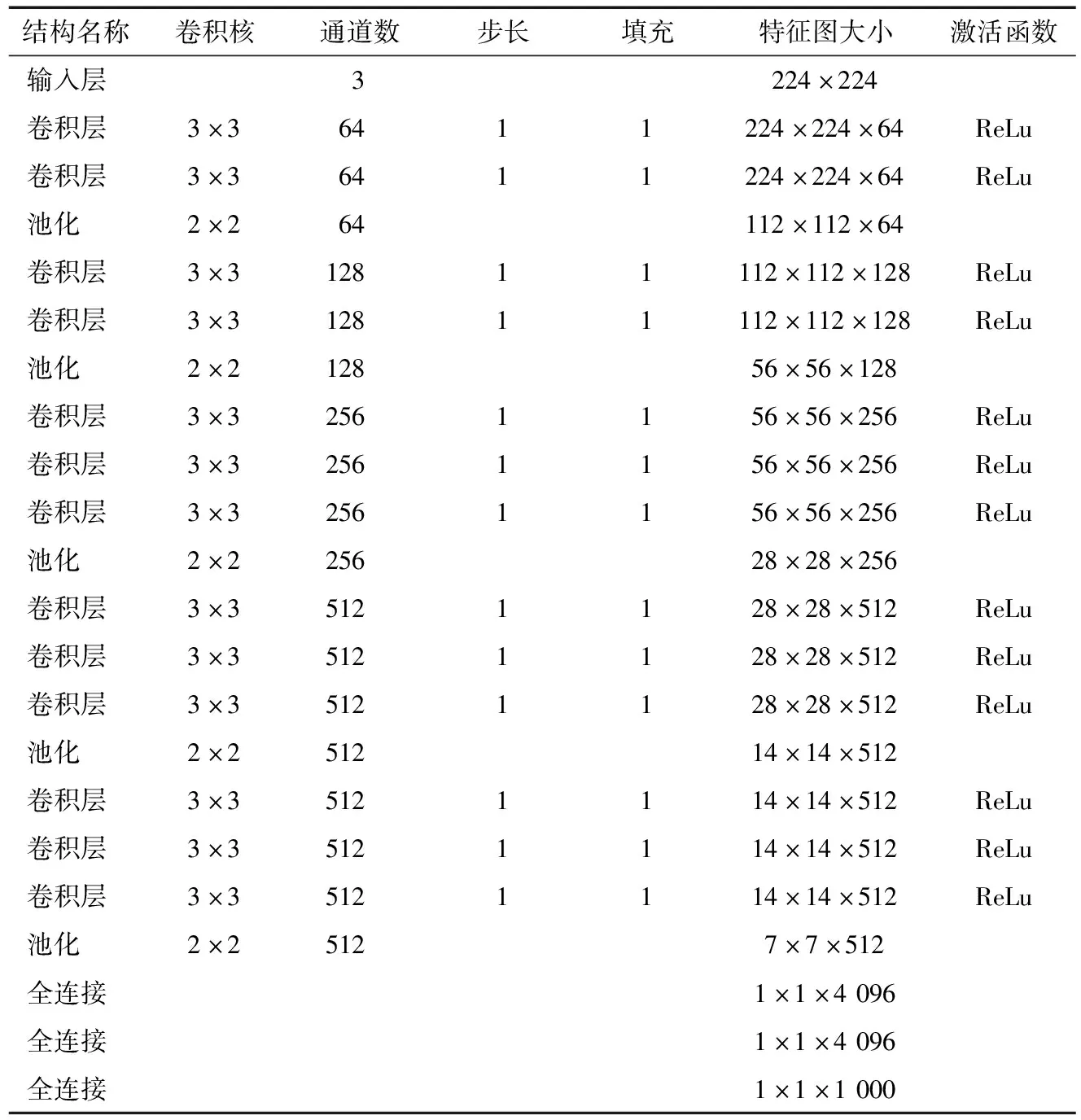
表3 Vgg16模型结构

3.2.2 迁移学习传统的数据挖掘和机器学习算法使用带标签或不带标签的数据集，统计模型对未来数据进行预测。半监督分类使用大量未标注的数据集和少量标注数据集，解决标签数据集太少而无法训练良好的分类器的问题，大多数是基于假设标记样本和未标记样本具有相同的分布。然而在实际应用中，搜集样本费时费力，带标签的训练样本数量更是有限，所以服从统一分布的数据的假设很难满足。统计模型必须根据不同数据分布重构模型，重构模型和重采集训练样本的代价太大。针对以上问题，迁移学习可以解决数据重采集和模型重构的问题，而且迁移学习还可以实现异类数据集之间的知识转移[13]。迁移学习的动机是人们可以智能地应用以前学习到的知识来更快地解决新的问题，或者有更好的解决方案。

3.2.3 池化层设计为在保留图像轮廓的完整性的同时，尽可能多地保留图像特征信息，文中结合最大池化与平均池化的优点提出最大—均值池化方式。通过式(7)和式(8)分别定义最大池化和平均池化的数学表达式：

(7)

(8)

式中：

xm——得到图像的滑动窗口n个像素点中的第m个像素点；

m——在滑动窗口中的位置。

池化方式是将xm映射到对应的统计值。

通过联合两者的优点，将最大池化方式和平均池化方式分别以权重相加得到新的池化方式——最大—均值池化。其数学表达式可表示为：

(9)

式中：

α+β=1。

3.2.4 激活函数设计为了解决ReLU激活函数存在的“神经元死亡”和输出偏移问题，提高网络模型的分类性能，提出一种基于ReLU激活函数与Tanh激活函数改进的激活函数TReLU。其数学表达式：

(10)

式中：

α——可调参数。

3.2.5 参数优化方法反向传播技术的使用使得深层神经网络的训练成为可能，基本原理是通过实际输出与期望输出计算出误差，并采用梯度下降法计算出误差函数相对于权值参数的梯度；然后在损失函数梯度的反方向上更新权值，假设有m个数据样本{(x1,y1),…,(xm,ym)}，对于单个样本(x,y)的损失函数定义为：

(11)

式中：

ω——连接权值；

b——偏置；

hω,b(x)——网络实际输出；

y——网络的期望输出。

对于整个样本数据集m的整体损失函数可以表示为：

(12)

式中：

ω——权值矩阵；

nl——网络层数；

sl——对应网络层神经元数目；

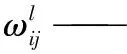
λ——权值衰减参数。

梯度下降法在计算梯度时只进行了一次权值更新，所以处理大量数据时其收敛速度很慢。针对上述问题提出了几种优化梯度下降法的方法。

(1)随机梯度下降法：随机梯度下降法(SGD)的基本原理是参数更新都是随机从训练集中选取[14]，更新迭代公式：

θ=θ-η·∇θJ(θ;xi;yi)，

(13)

式中：

η——学习率；

xi、yi——训练样本；

θ——训练参数。

随机梯度下降法的优点在于频繁的参数更新使得参数间具有高方差，这有助于网络收敛到最优解。但缺点是参数的更新都是随机从训练集中选取，每次的参数更新方向具有随机性，增加了网络的迭代次数，使网络收敛速度变得缓慢。

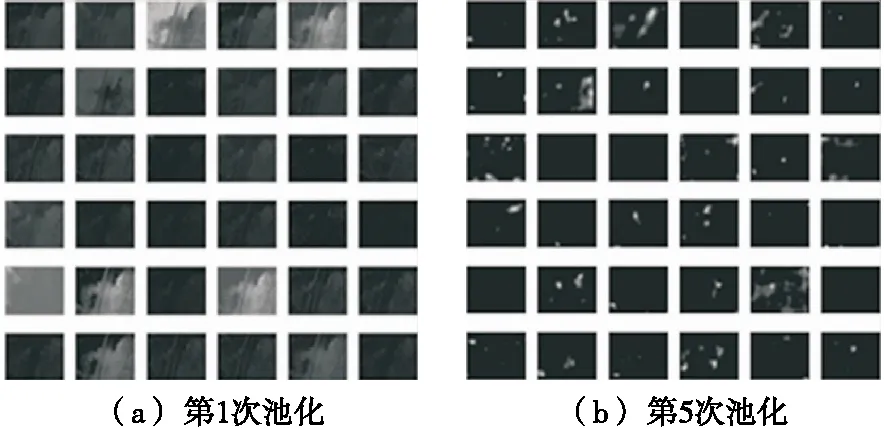
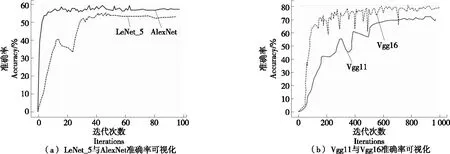
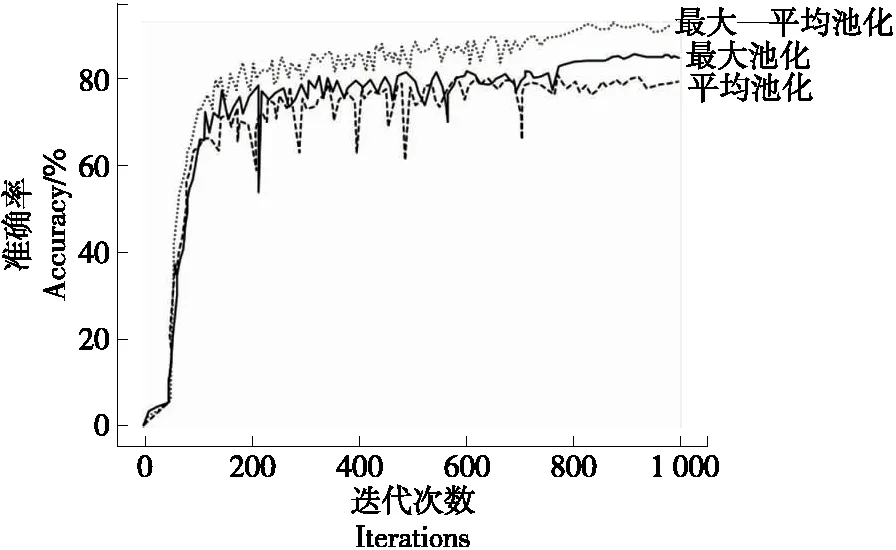
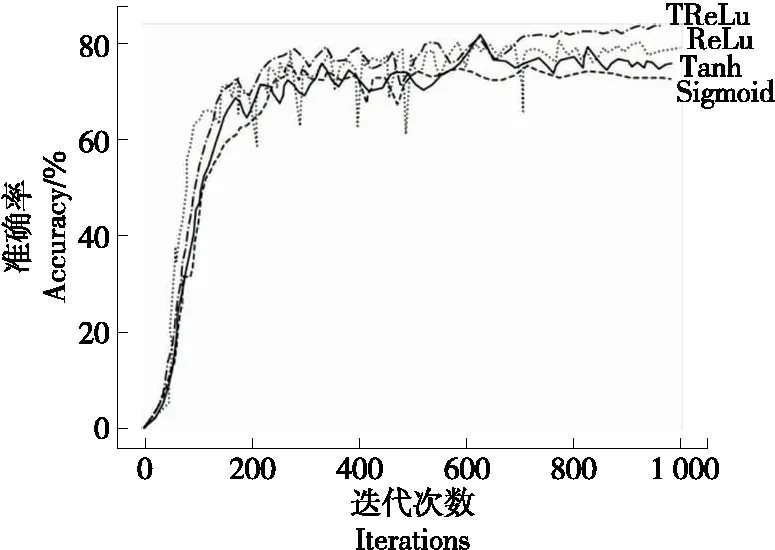
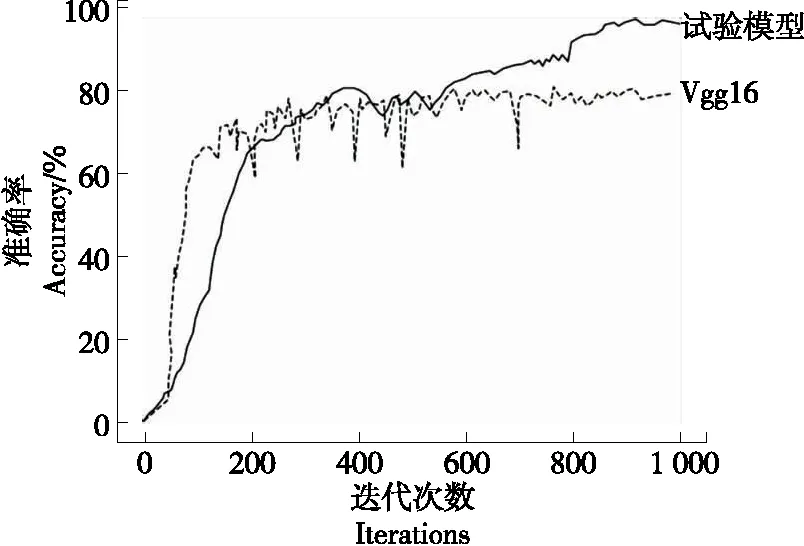
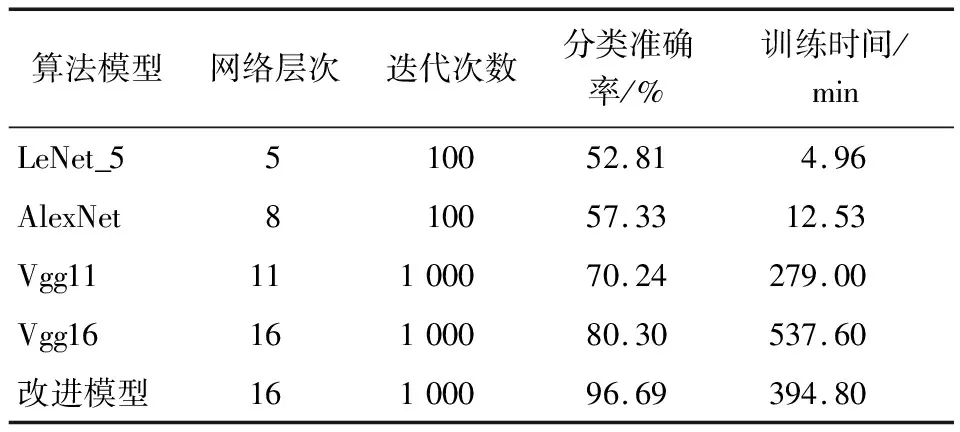
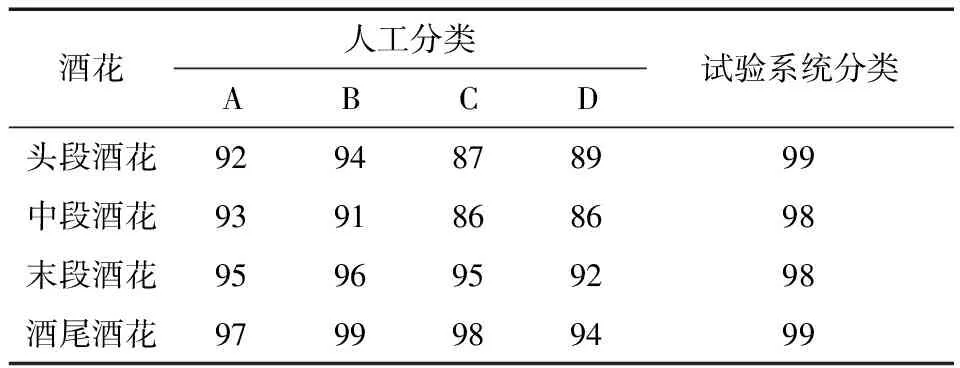
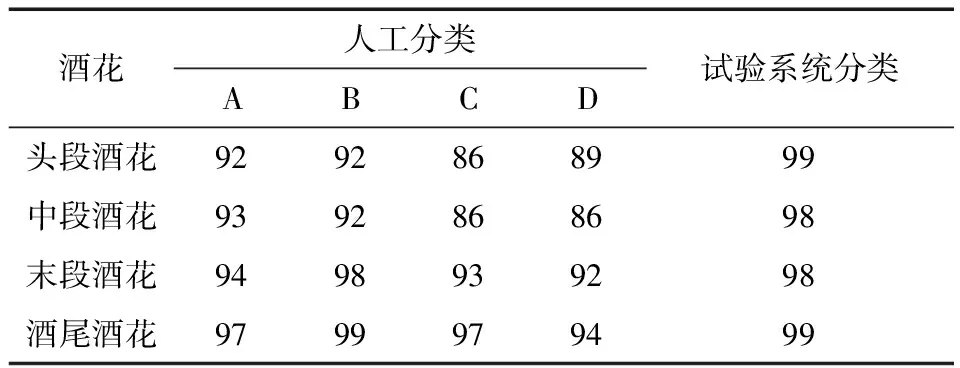
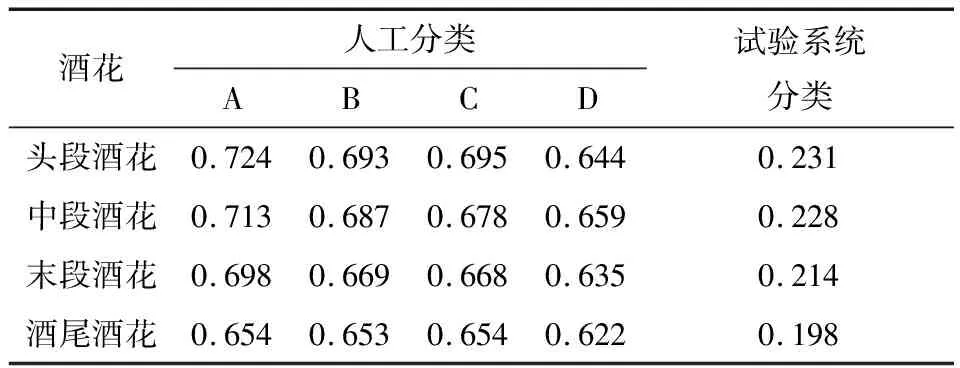
(2)小批次随机梯度下降法：小批次随机梯度下降法的提出是为了缓解随机梯度下降法中网络迭代次数增加和网络收敛速度缓慢的问题，在参数更新速度和更新次数间取得一个平衡[15]，在参数每次的更新过程中会从训练集中随机选取m(m

θ=θ-η·∇θJ(θ;xi:i+m;yi:i+m)，

(14)

式中：

η——学习率；

xi:i+m、yi:i+m——训练样本；

θ——训练参数动量因子方法。

由于梯度下降法在应用过程中伴随着高方差振荡，这使得网络很难稳定收敛，因此研究者[16]提出了动量技术来缓解网络收敛不稳定的问题，数学表达：

vt=μvt-1+η∇θJ(θ)，

(15)

θ=θ-vt，

(16)

式中：

μ——0～1的动量因子；

vt-1——上一次的更新值。

选用小批次随机梯度下降法，加入动量因子对小批次随机梯度下降法，减少计算量，加快网络收敛。

3.3 最终模型结构

文中改进模型是基于Vgg16大框架下进行改进，该模型结构框图如图8所示。

在图8中，卷积核初始化方式采用基于权重的迁移学习，池化方式采用改进后的最大—均值池化方式，激活函数采用改进后的TReLU激活函数。

图8 改进模型结构

4 试验结果分析

4.1 试验平台

试验基于操作系统windows 1064，处理器Intel(R)core(TM)i5-8300H CPU @ 2.30GHZ，内存8.00 GB，显卡NVIDIA GeForce GTX 1050的开发平台，采用python + tensorflow + pycharm作为开发环境。

4.2 试验结果及其分析

整个试验部分使用的数据集，如无特别说明都采用以下数据集，从构建的酒花数据集中选取头段酒花、中段酒花、末段酒花、酒尾酒花图片各1 000张。其中70%作为训练集，30%作为测试集，图片大小为544×960×3。

模型采用改进Vgg16+迁移学习，图像输入要经过5次池化，由模型结构可以推出第1，2，3，4，5次池化的特征图个数分别为64，128，256，512，512。由于篇幅有限文中展示第1次和第5次池化后的部分特征图，如图9所示。1∶1特征融合图，如图10所示。

图9 池化后的特征图

由图10可知，最初卷积提取到的特征比较全面，图像纹理边缘信息比较清楚，随着卷积的深入，特征图越来越抽象。第1次池化后特征提取的信息比较全面，特征融合过后能够看见较清楚的酒花。第5次池化后图像变得模糊，高级特征肉眼不可见，特征融合后图像也比较抽象，肉眼基本无法看见酒花。

图10 1∶1特征融合图

4.2.1 经典模型分类结果为了验证现有经典模型对白酒酒花的分类效果，直接将预处理后的酒花图像输入到模型中，对其准确率和迭代步数进行比较。试验仿真结果如图11所示。

由图11(a)可以看出，LeNet_5、AlexNet网络深度浅，分别是5层和8层，在迭代次数较少的情况下就达到饱和，对于一些简单的分类任务能够达到很高的准确率。但酒花分类准确率远低于人工分类，达不到分类精度要求。由图11(b)可以看出，随着卷积网络深度的加深，分类准确率逐渐提高，但仍然达不到酒花分类的精度要求，且相应的训练时间也变长。

图11 经典模型分类结果

4.2.2 基于改进池化方式的准确率对比为验证改进池化方式的有效性，在传统Vgg16框架的基础上，改变不同的池化方式，验证其在白酒酒花分类的准确率。试验结果如图12所示。

单一的池化方式不能完全考虑图像特征信息，平均池化更多地保留了图像的背景信息，忽略了图像中的纹理信息，相反最大池化则更多地保留了纹理信息，因为酒花特征对纹理要求高，从图12可以看出最大池化的准确率略大于平均池化的。但两种方法对酒花分类准确率明显低于改进的池化方法，因为改进的方法综合考虑了背景与纹理信息。

图12 不同池化方式准确率对比

4.2.3 基于改进激活函数的准确率对比为验证改进激活的有效性，在传统Vgg16框架的基础上，使用不同的激活函数，验证其在白酒酒花分类的准确率。试验结果如图13所示。

图13 不同激活函数准确率对比

Sigmoid函数与Tanh函数容易产生梯度消失的情况，ReLU函数在反向传播过程中会出现神经元死亡。从图14可以看出，改进的激活函数分类准确率高于其他几种激活函数。

4.2.4 最终模型与传统Vgg16模型准确率对比最终模型结构包括Vgg16框架+迁移学习+改进池化方式+改进激活函数，为验证改进模型的有效性，将其与原始Vgg16模型进行对比。试验结果如图14所示。

从图14可以看出，基于Vgg16改进的卷积神经网络模型，对白酒酒花数据集分类准确率有明显的提升，未改进前分类准确率为80.30%，改进后分类准确率为96.69%，改进后的分类准确率能够达到白酒生产的实时性要求。改进模型与传统模型试验结果对比如表4所示。

图14 改进模型准确率

从表4可以看出，LeNet_5、AlexNet网络深度浅，训练时间短，分类准确率低，Vgg11和Vgg16随着层数增加分类准确率明显提高，但训练时间较长，改进模型在分类准确率与训练时间取得了一个平衡，且分类准确率高于其他几种分类模型。

表4 改进模型与传统模型试验结果对比

4.2.5 人工分类对比试验从头段酒花、中段酒花、末段酒花、酒尾酒花分别选取100张组成人工分类和试验系统分类对比的数据集。将400张酒花图片的标签隐藏并且将图片随机排序，从生产线上请2位经验丰富的摘酒师傅A和B，再请2位年轻的摘酒师傅C和D对此次试验数据集进行2次分类，第1次分类试验结果如表5所示。

第2次试验使用同样的数据集，告知4位摘酒师傅数据集已经改变，试验分类结果如表6所示。

从表5和表6可以看出，无论是人工分类还是试验系统分类在没有时间的要求下分类准确率基本都能达到90%以上；经验不同的员工分类准确率高低不同，同一工人在不同时间准确率也会有波动，人工分类具有不稳定性，而机器视觉的分类精度高且稳定，因此试验系统分类算法相比人工分类具有一定的优越性。