基于GAPSO-TS 的多基地无人机航路-时间协同规划*

杨川力，宁 芊*，陈炳才，雷印杰

（1.四川大学电子信息学院，成都 610065；2.大连理工大学计算机科学与技术学院，辽宁 大连 116024）

0 引言

由于军事侦察任务的复杂性越来越高，侦察方法朝着多无人机合作的方向逐渐发展［1］，因此，多无人机协同规划十分重要。并且多种无人机协作作战是无人机在战场上作战的主要形式［2］，多无人机要综合考虑任务点分配，无人机通信，编队保持，碰撞避免，雷达威胁，以及时间等问题。因此，多无人机的航路规划比单无人机航路规划更加复杂和困难。时间协同对于多无人机执行搜索，攻击等任务是极其重要的，可以有效提高任务完成率［3］。

目前，很多研究都是关于单无人机的航路规划，如某些经典算法细胞分解法（CD）、人工势场法（APF）等算法［4］。还有一些智能反应算法，如遗传算法（GA）、粒子群优化算法（PSO）［5］。遗传算法是由Holland 于20 世纪70 年代初提出，目前，该算法已经在各个领域得到应用［6］。文献［7］把遗传算法和概率自动结合，解决无人机在未知空域中路径规划实时性和适用性不足的问题。文献［8］混合了A*算法和遗传算法，提高了基本遗传算法的稳定性和效率。粒子群算法（PSO）是一种基于自然现象的启发式算法，采用了鱼群和鸟群等生物的社会行为，粒子群算法结构简单，便于实现，但收敛速度慢，容易陷入局部最优［9］。文献［10］引入QPSO 算法，对基本PSO 算法进行改进，提高了全局搜索能力。遗传粒子群算法（GAPSO）混合了遗传算法和粒子群优化算法，该算法首先计算适应度函数值，对群体中的个体按适应度函数值的大小进行排序，再采用PSO 算法对群体中的优秀个体进行提高，提高以后的个体被保留并进入下一代，其他适应度函数值差的个体则被淘汰。对已经提高的优秀个体再通过选择交叉和变异步骤得到剩下的个体［11］。

本文同时考虑航路规划和时间协同规划，引入了禁忌搜索算法（Tabu-Search）到GAPSO 中，提出一种遗传粒子群算法和禁忌搜索算法组合的GAPSO-TS 算法，由于GAPSO 算法是基于群体的优化算法，而禁忌搜索算法是基于个体的［12］，组合算法保证了搜索的多样性和全局性。

由于各个无人机距任务点距离不同，不能保证所有的无人机都能在协同时间内到达目的地，所以，需要对不满足条件的无人机重新规划航路。目前主要有两个方面来解决此问题，一是以变步长来调整无人机的协同时间；二是以延长航路来达到时间协同［13］。本文对于不满足协同时间的无人机，设计了以协同时间或协同航程为约束的适应度函数，重新规划航路，以此保证所有无人机都能在最短时间内同时到达目标点。

1 无人机航路规划问题建模

1.1 问题描述

面对多基地多无人机最短时间同时到达目标点的任务需求，本文研究多无人机时间协同规划问题。单无人机在执行任务的过程，会碰到很多威胁，包括雷达、地形障碍、防空火炮等。如图1 所示，仿真实验中设定的场景包括了威胁区域、起点、任务点、地形。多无人机规划是在单无人机规划的基础上建立的。

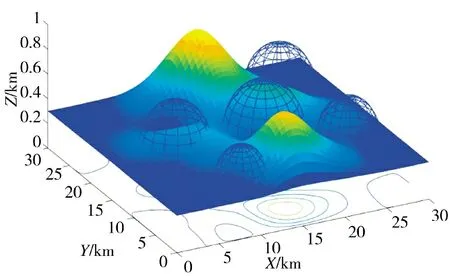
图1 无人机飞行环境

威胁区域用定义为蓝色半球体，威胁区域的中心坐标为（x，y，z），第i 个威胁区域的半径为Ri。地形由山丘和平原组成。

1.2 航行代价评估

式（1）为单无人机航迹规划时的适应度函数，式（2）为多无人机协同规划时，对无法协同的无人机设计的新适应度函数。

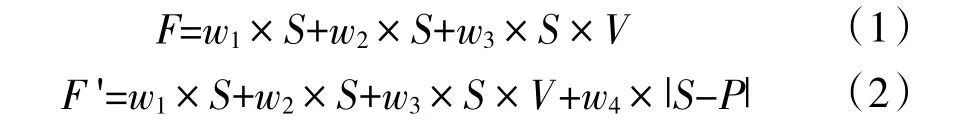
1）油耗代价：w1×S

w1是油耗的权重，S 是该航路的实际长度。

2）高度代价：w2×H

w2是高度代价的权重，H=∑Hi，表示所有航路点的高度代价的总和，Hi表示航路点i 的高度代价，用式（3）来计算，Hmax、Hmin为最高和最低飞行高度，h是当前航路点的高度，Cdestory是惩罚因子。

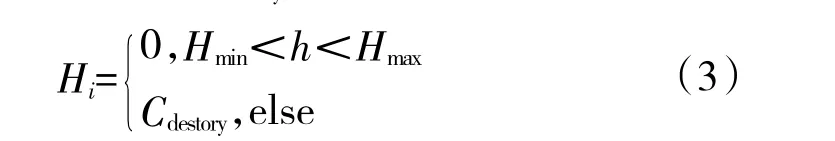
3）威胁代价：w3×S×V

w3是威胁代价的权重，S 是实际航路的长度，V 是所有航路点的威胁系数，Vij是第k 段航路中第i 个点到第j 个威胁区域的威胁系数。总的威胁系数是每段航路k 上的各点的威胁系数取平均值，再对所有航路的威胁系数进行求和，用式（4）计算。

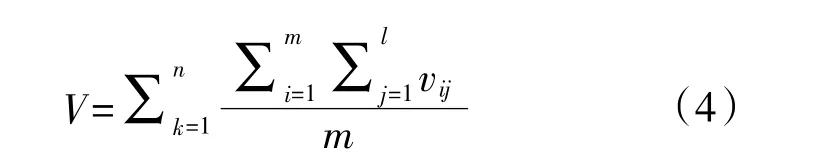
vij用式（5）计算，其中，Dij是点Pk，m到威胁j 的直线距离，Rj是威胁j 的半径，如下页图2 所示。

图2 航迹威胁图

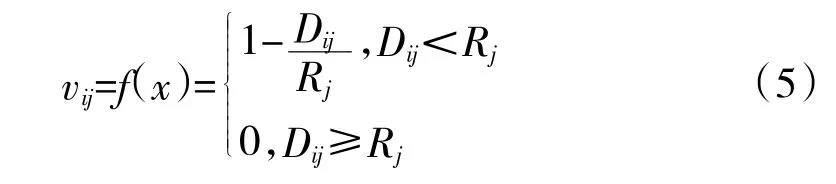
4）重新规划航路代价：w4×|S-P|

w4航路约束代价的权重，S 是实际规划航路的长度，P 是根据最短协同时间设计的航路约束计算方式，tc是协同时间，Vmax是无人机最大运行速度，cs是航路约束系数。

2 基于GAPSO-TS 的航路规划模型

GAPSO 算法是把GA 和PSO 算法结合起来，利用PSO 粒子间的相互联系可以快速成熟的特点和GA 交叉、变异的特点，提高算法的收敛速度和精度［11］。在多无人机规划中，需要进一步提高算法的收敛速度和精度，本文在GAPSO 算法的基础上引入了禁忌搜索算法（Tabu-Search）。

禁忌搜索算法是对个体进行优化，通过搜索个体的邻域来获取最优解，并将已经访问过的邻居放入禁忌表，防止重复访问导致其陷入搜索循环，同时，会特赦禁忌表中的优良状态来保证搜索的多样性与全局性［14］。

2.1 状态空间模型

本文通过无人机在第i 个航路点的航偏角αi、俯仰角βi和飞行时间Ti建立极坐标系（α，β，T）与三维坐标系（x，y，z）的状态空间模型，极坐标转换为三维坐标用式（7）计算。

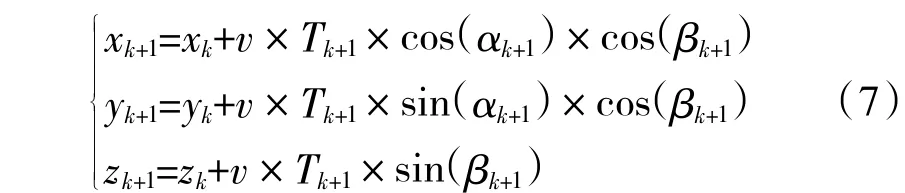
（xk+1，yk+1，zk+1）表示三维空间中第k+1 段航路的坐标点，αk+1、yk+1、Tk+1分别是第k+1 段航路的航偏角和俯仰角以及每一段航路的运行时间，v 是无人机的平均飞行速度，（xk，yk，zk）是第k 段航路的三维坐标。使用极坐标初始化航路可以保证转角满足约束和航路平滑。

2.2 基本PSO 模型

假设一个粒子有D 维搜索空间，总共有n 个粒子，第i 个粒子的状态空间描述用向量Pi=

2.3 交叉和变异操作

采用浮点数交叉和变异［15］。设P1、P2是待交叉的粒子，交叉因子为Cp，子代为S1、S2，设α={αi1，…，αiD}，β={βi1，…，βiD}，T={Ti1，…，TiD}。则P1、P2的交叉操作为式（10），其中，x 是α、β、T 基因中的任意一个，S1（x）表示编号为1 的子代中的x 基因，P1（x）表示编号为1 的父代中的x 基因，S2（x）、P2（x）同上。

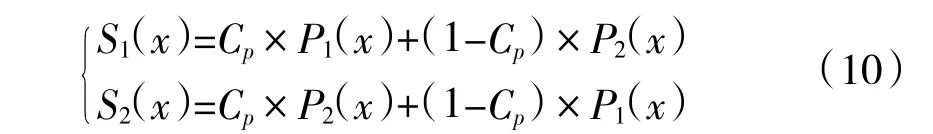
设变异因子为Cm，随机数r，变异操作用式（11）来计算变异后的结果。其中，xmax为基因x 的最大值，xmin为基因x 的最小值，S（x）为子代染色体的x 基因。

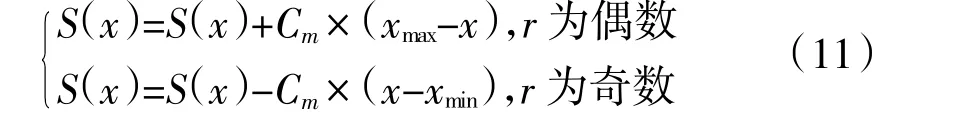
2.4 GAPSO-TS 算法步骤

1）初始化种群数为NP，粒子维数D，最大迭代次数tmax，随机初始化粒子的速度和状态。

2）根据式（1）计算粒子的适应度值，并更新历史最优和全局最优。

3）对全局最优引入TS 算法进行优化。

4）按适应度对所有粒子排序，保留前NP/2 的粒子，舍弃后NP/2 的粒子。

5）对前NP/2 的粒子进行交叉和变异操作。

6）判断是否满足迭代终止条件，满足，则输出最优解；否则，返回第2）步，算法流程如下页图3 所示。

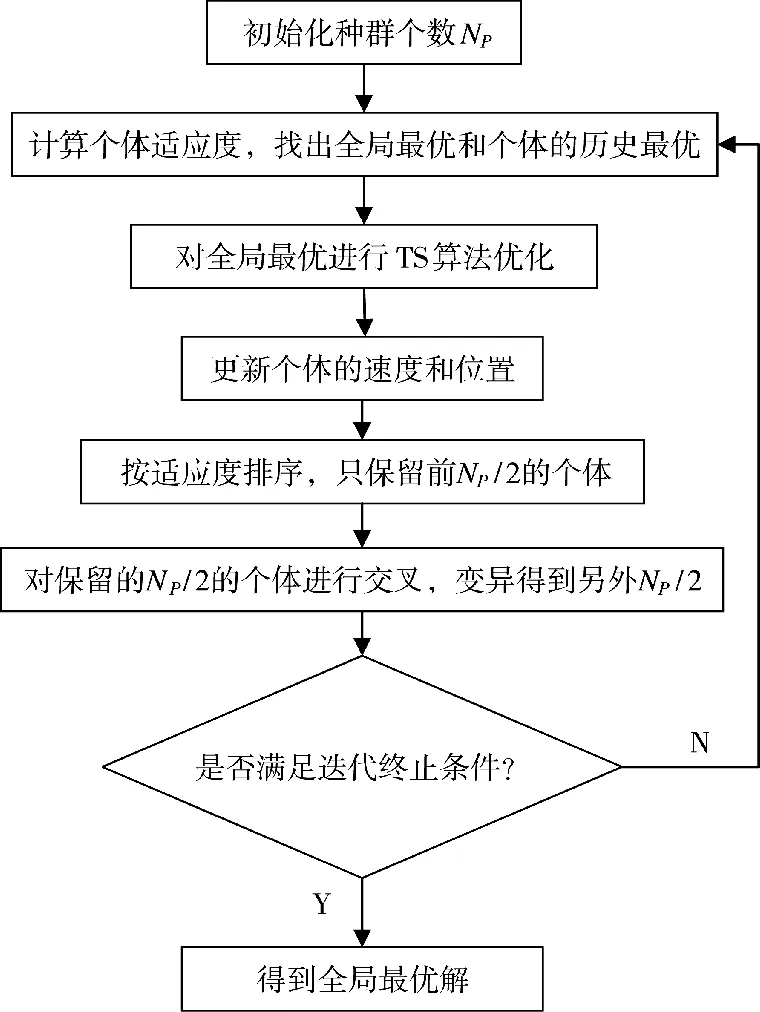
图3 GAPSO-TS 算法流程图

3 多无人机协同规划

3.1 多无人机协同规划模型

多无人机协同规划采用分层规划的模型，先对多个无人机用GAPSO-TS 算法进行航迹预规划，再进行协同规划，如图4 所示。

图4 是无人机协同规划模型，分为顶层协同规划层和底层无人机航迹规划层，先对每架无人机用GAPSO-TS 算法进行预规划，然后根据无人机飞行速度范围，把［Tmin，Tmax］时间窗口传递给协同规划层。

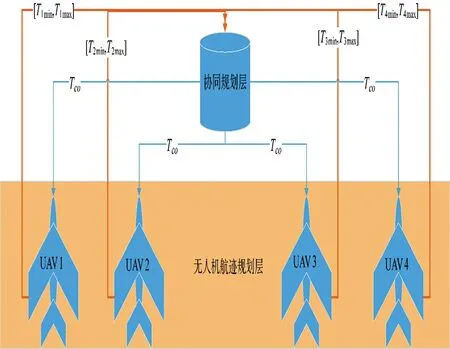
图4 多无人机协同规划模型

协同规划层根据各个无人机的时间集来计算协同时间，取协同时间为时间交集的下界，再把协同时间传递给各个无人机进行速度调整。若没有协同时间，则根据最短时间到达目的地原则，选取最长航路的无人机最短规划时间作为协同时间，对无法满足协同时间的无人机以协同时间为约束，变换适应度函数，进行航迹重规划。

3.2 多无人机协同规划算法

4 单机航路规划和多机航路规划仿真

4.1 仿真环境

在IntelCorei5（TM）-7500@3.4 GHz，8 G 内存的硬件，Matlab 仿真软件环境下进行仿真实验。场景参数由下页表1 所示。

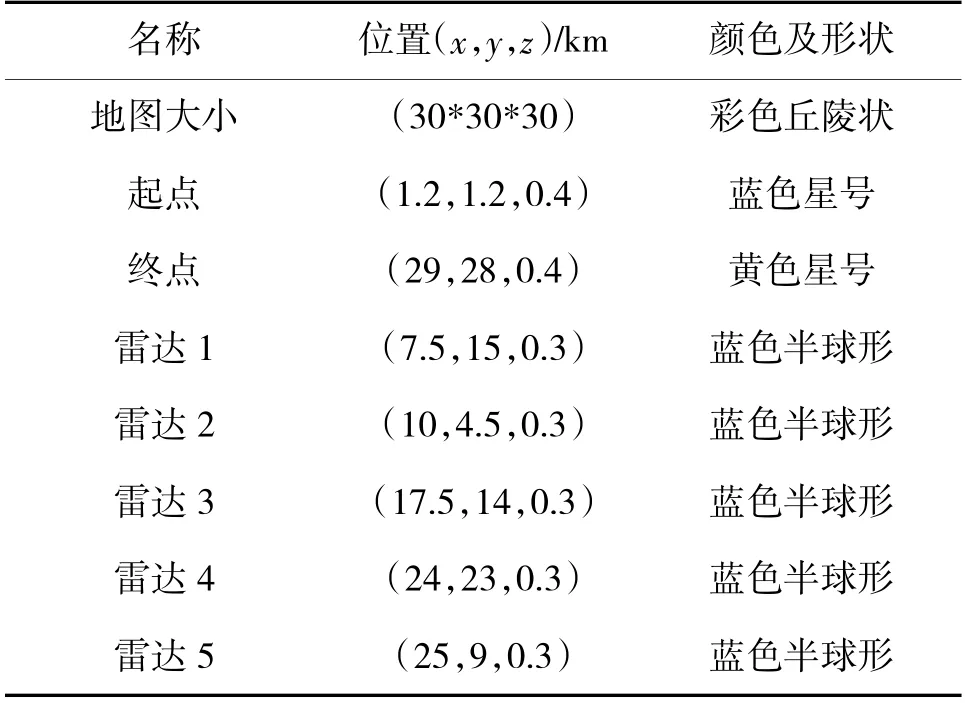
表1 场景参数表

4.2 单无人机三维空间仿真结果与分析

把GAPSO-TS 算法、标准PSO 与GAPSO 算法作对比，仿真结果如图6～图8 所示。

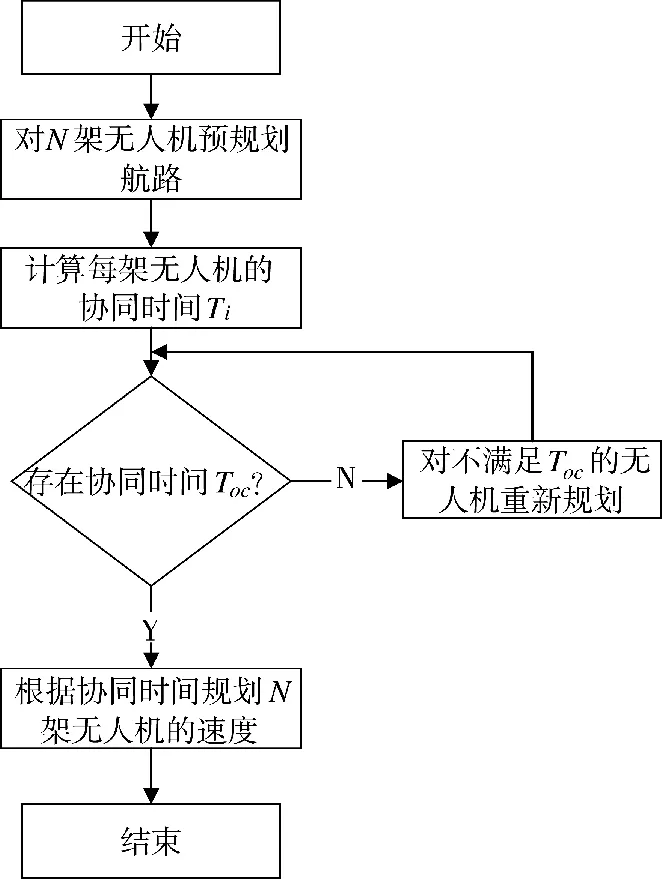
图5 多基地无人机协同规划流程图

从图8 分析，GAPSO 算法由于收敛很快，导致局部最优，PSO 算法收敛速度次于GAPSO 因此，种群多样性丰富，随着迭代次数增加，适应度精度比GAPSO 高，GAPSO-TS 算法继承了GAPSO 收敛快的特点以及禁忌搜索的多样性，在收敛速度和精度上都有所提高。从图6、图7 中3 组算法运行的结果看，PSO 算法运行的航迹通过爬高绕过威胁，GAPSO 和GAPSO-TS 算法的航迹相似，也避开了威胁，但GAPSO-TS 算法的航迹高度更低，说明GAPSO-TS 的全局寻优能力高于GAPSO。

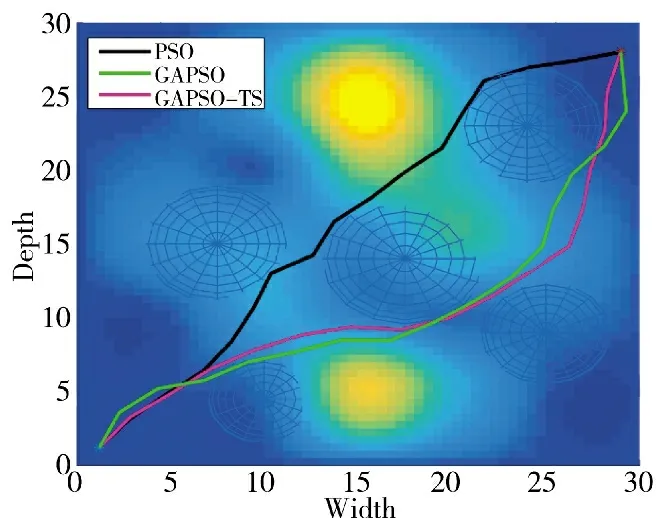
图6 GAPSO-TS，PSO，GAPSO 算法航迹比较俯视图

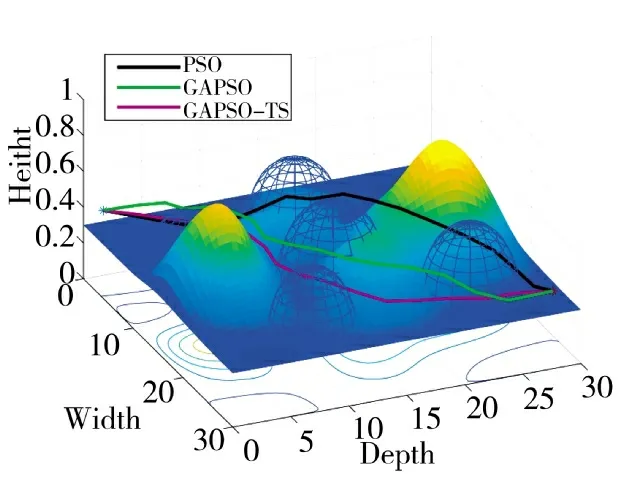
图7 GAPSO-TS，PSO，GAPSO 算法航迹比较侧视图

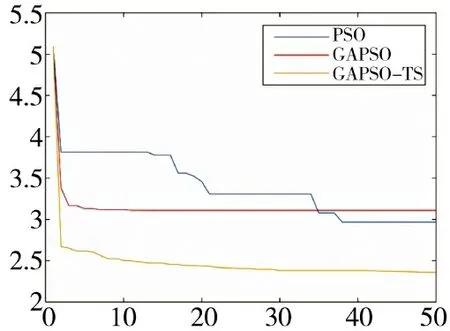
图8 GAPSO-TS，PSO，GAPSO 适应度比较图

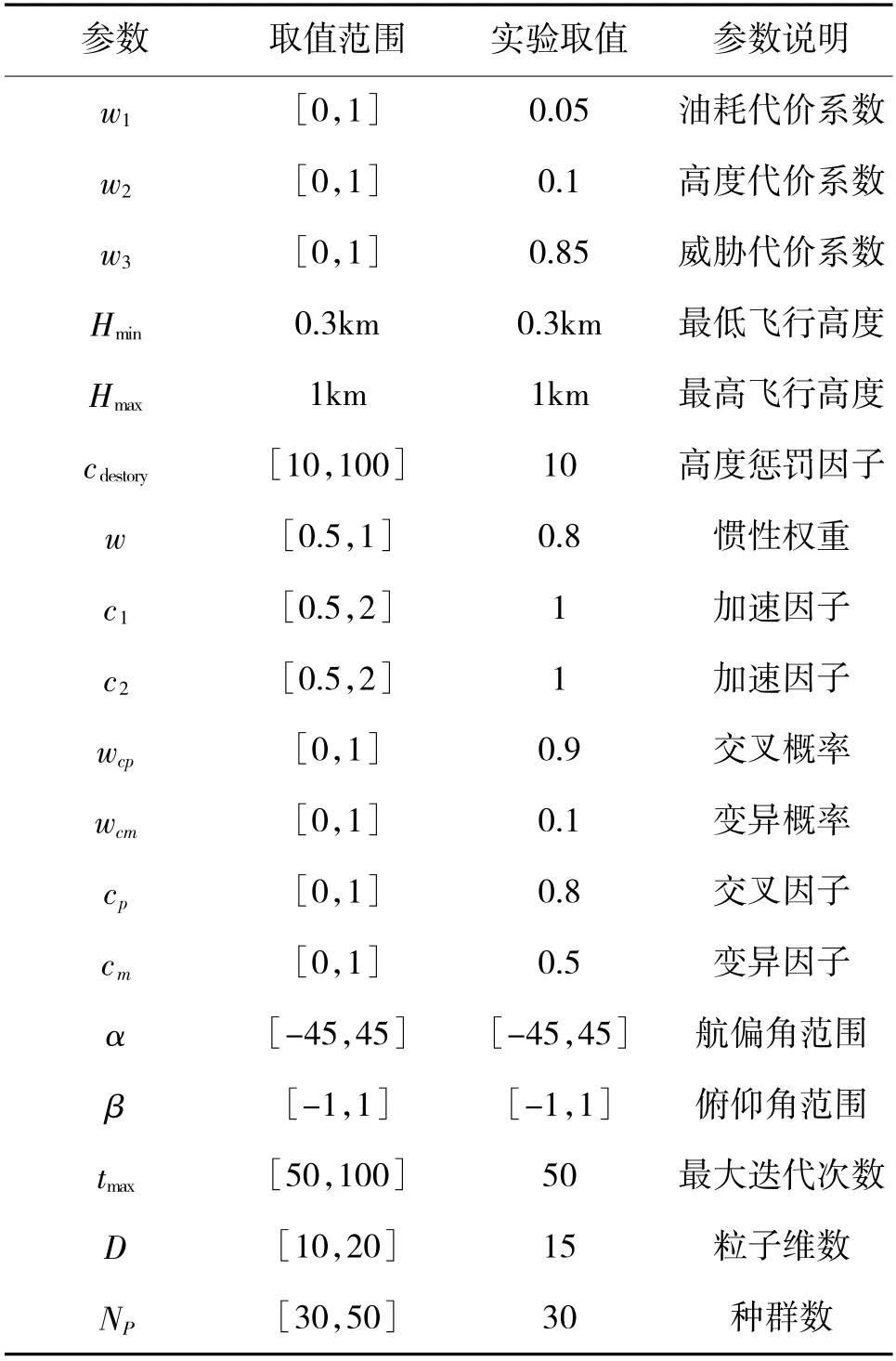
表2 实验参数表

表3 是 做10 次 实 验 的 结 果，PSO、GAPSO、GAPSO-TS 算法的适应度都用式（1）来计算，标准差公式用式（11）来计算，其中，σ 为标准差，n 设为10，fi是第i 次实验的适应度值，f 是平均适应度值，收敛速度定义为f（i）与f（tmax）之间的误差为10%时的最小迭代次数的倒数。GAPSO-TS 算法在精度上比PSO 算法提升了14%，比GAPSO 算法提高了25%，从标准差来看，GAPSO-TS 算法的稳定性要优于PSO 和GAPSO 算法。

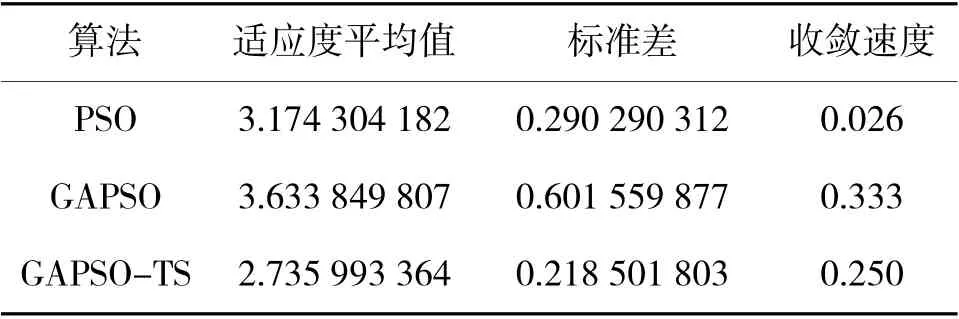
表3 航迹规划适应度比较

4.3 多无人机三维空间协同规划仿真参数设置

为了验证多无人机协同算法的性能，假设4 架无人机从不同位置出发，到达相同目的地。地形、雷达参数如表1 所示，多无人机协同规划模型参数见下页表4。

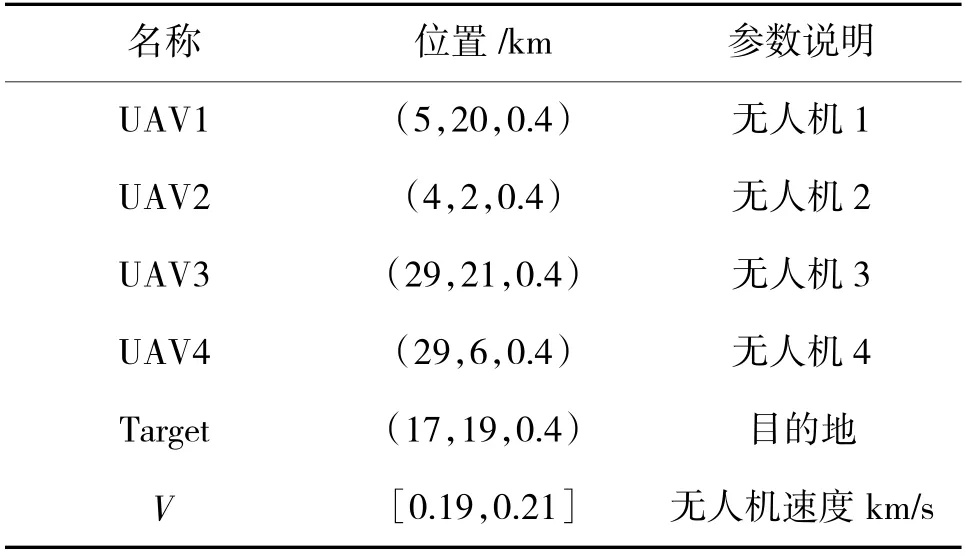
表4 无人机参数

4.4 多无人机协同规划仿真结果与分析

4.4.1 多无人机协同规划仿真实验

通过下页图9、图10 可以看出，各个无人机从起点到目标点完成了航路规划，从图11 和表5 的实验结果中看到，协同时间为86.058 07 s，UAV3 的最大飞行时间为69.978 27 s，不满足时间协同的要求，所以要重新规划，UAV3 重新规划的适应度函数设为式（2），式（2）中航路约束系数cs用来限制航路长度，通过设置不同大小的cs作对比来验证式（2）的有效性。

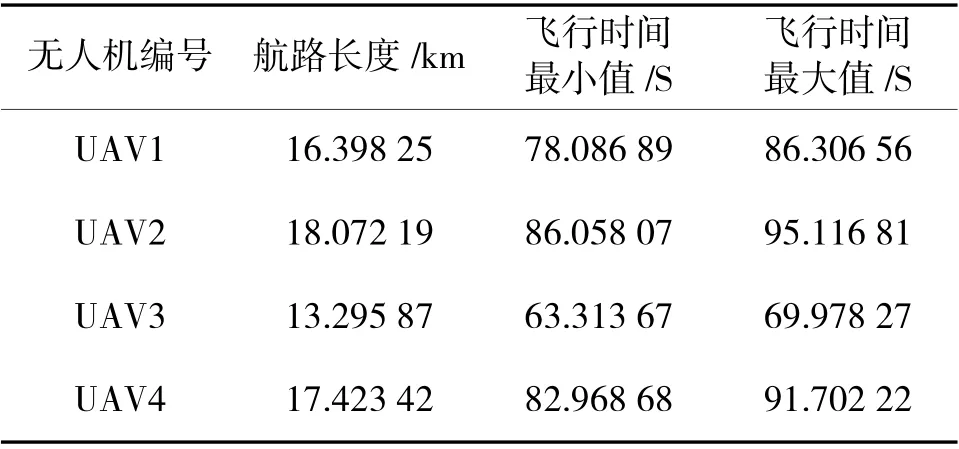
表5 各无人机航迹规划时间

图9 多基地无人机协同规划航迹侧视图

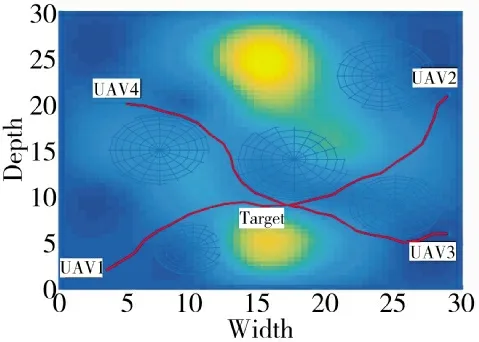
图10 多基地无人机协同规划航迹俯视图

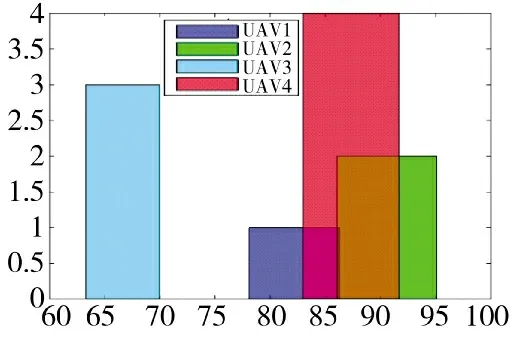
图11 多基地无人机时间窗口

4.4.2 cs=1 时的无人机协同规划仿真

UAV3 重新规划的轨迹如图13 中的黑色虚线所示所示，从图中可以看出UAV3 的航迹延长了，从图12 来看，UAV3 的航迹沿着地形航行来增加航路距离，结合表6 和图14 来看，根据最长航迹最短时间设为协同时间的原则，协同时间设为86.05 s，而UAV3 重新规划的最大飞行时间是86.06 s，大于协同时间，验证了协同规划的有效性。

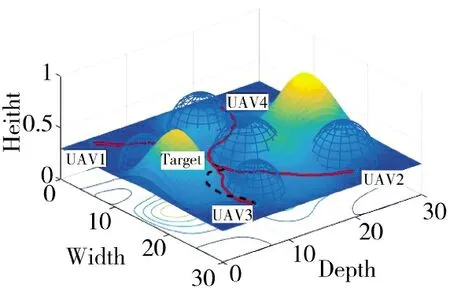
图12 UAV3 重规划侧视图

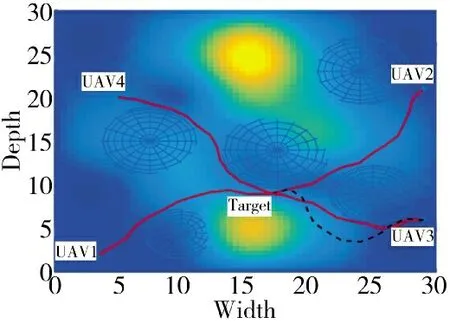
图13 UAV3 重规划俯视图

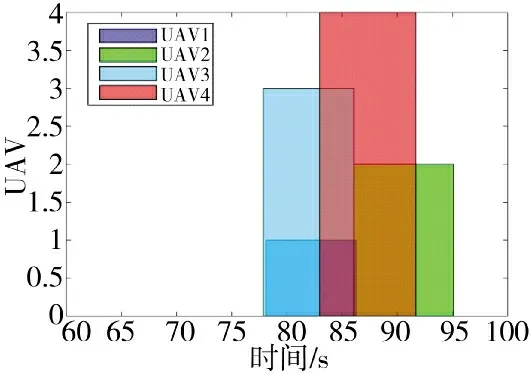
图14 重规划多基地无人机时间窗口

表6 各无人机航迹规划时间

4.4.3 cs=1.02 时的无人机协同规划仿真

当cs=1.02，UAV3 重新规划的航路是图16 中的绿色虚线所示，从图15 中的绿色虚线看出，UAV3重新规划的航路跟随了地形的同时并延长了航路，根据表6 和表7 对比发现，cs=1 时，UAV3 航路长度为16.351 66 km，cs=1.02 的UAV3 航路长度为16.681 12 km，在航路长度上略有增加，从图15 容易看到UAV3 的时间窗口相对于图14 右移了一点，增加了裕量，这样可以保证协同到达的稳定性。对比实验的结果验证了式（2）的有效性。

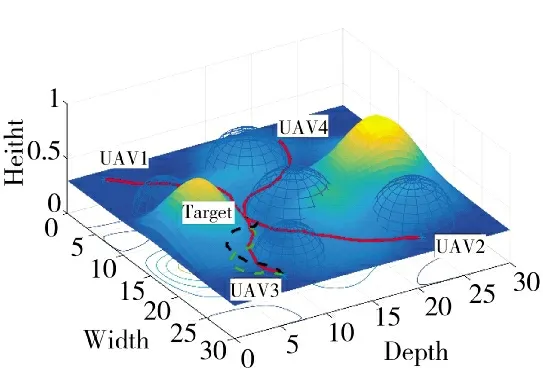
图15 UAV3 重规划侧视图

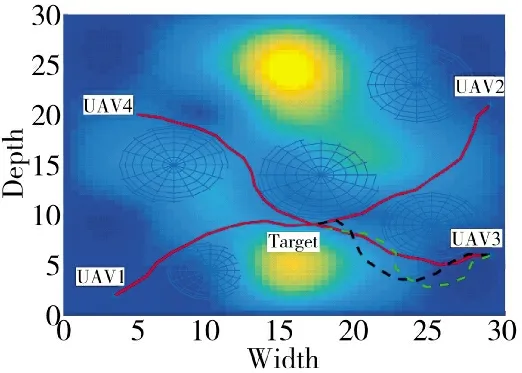
图16 UAV3 重规划俯视图

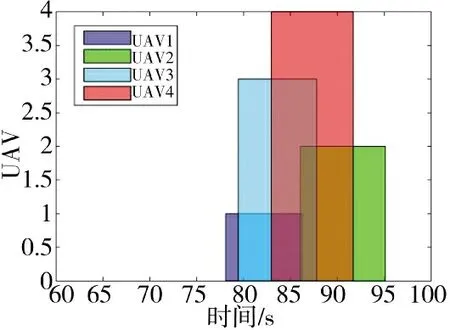
图17 重规划多基地无人机时间窗口

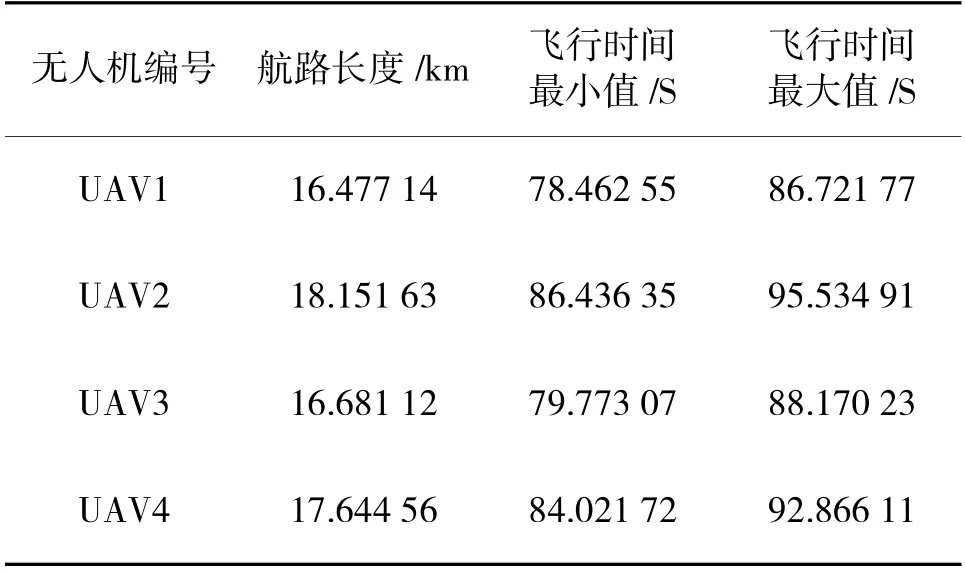
表7 重规划后的各无人机规划时间

5 结论

本文通过引入禁忌搜索算法，提升了GAPSO算法的收敛速度和精度，通过对比实验，验证了GAPSO-TS 算法的有效性。

通过建立多无人机分层模型，设计了新的适应度函数，对不满足时间协同的无人机进行重规划，能够实现多基地无人机目的地集结的时间同步，证明了多无人机时间协同规划算法的有效性。复杂环境中的多机规划是一个多变量、多状态、多约束、多目标的复杂系统规划问题，本文还存在不足，可以在本文的基础上运用马尔科夫链等随机过程模型，进一步将生存状态模型与评估、威胁模型与评估等与航路-任务规划相结合。