基于特征建模的模型恢复抗饱和控制*
2021-11-17郭瑞科
郭瑞科 胡 军
北京控制工程研究所,北京 100190
0 引言
工程实践中,控制器往往通过执行机构驱动被控对象,而执行机构自身的物理或者能量约束决定了其输出存在限制,如果控制器给出的控制指令超出了该限制,会导致控制器的输出和被控对象的输入不一致,也就是存在控制输入饱和约束。从执行机构角度看,就是执行器存在饱和非线性约束,当控制系统发生执行器饱和时,可能会导致控制动态性能变差,甚至闭环系统不稳定。通过设计抗饱和补偿器恢复闭环系统控制性能和闭环系统稳定性,是一种行之有效的抗饱和控制方法[1]。
常见的抗饱和控制方法有直接线性抗饱和(Direct Linear Anti-Windup, DLAW)和模型恢复抗饱和(Model Recovery Anti-Windup, MRAW)[2]。DLAW方法通过求解线性矩阵不等式来设计抗饱和补偿器以保证一定的控制性能和闭环系统稳定性,往往会转化为规模较大的线性矩阵不等式,计算量大,设计较复杂。MRAW方法中抗饱和补偿器使用与被控对象相同的模型,并且补偿器的求解不依赖于控制器,设计简单,有较大的设计自由度[3]。
目前基于MRAW方法的抗饱和设计研究主要针对连续对象,研究离散系统的较少[4-8]。Zaccarian等针对开放水道控制系统中调节水流的闸门存在饱和约束的临界稳定系统,分别考虑了控制器和被控对象在连续和离散时间情况下的抗饱和设计问题,给出了临界饱和系统的MRAW抗饱和补偿器设计算法[9]。Ramos等研究了重复控制中的模型恢复抗饱和问题,设计了不受控制器影响的简单低阶抗饱和补偿策略,给出了基于最优控制的抗饱和增益求解线性矩阵不等式条件[10]。谭翠兰等针对并网逆变器控制中容易出现积分饱和的现象,设计了分别补偿控制量和输出反馈量的离散MRAW抗饱和补偿器[11]。刘田禾等在建立高超声速飞行器姿态控制切换系统模型的基础上,提出抗饱和切换控制方法,通过求解一系列LMI来设计静态抗饱和补偿器[12],但求解数量众多的LMI会增加计算负担。类似的,杜立夫等人针对高超声速飞行器纵向模型,设计了基于鲁棒控制的抗饱和补偿器,也存在求解复杂LMI的问题[13]。韩少君等针对火星飞机操纵机构存在控制能力受限问题,提出基于扩张状态观测器的符合抗饱和策略,这种设计方法会增加控制器设计的复杂度[14]。前述基于MRAW抗饱和设计都是针对低阶线性离散系统设计,鲜有涉及非线性系统或者高阶被控对象,即使针对部分此类对象设计MRAW抗饱和补偿器,也会由于补偿器与被控对象使用相同的动态,有较大的设计复杂度和难度。
吴宏鑫和胡军提出了根据对象动力学特性、环境特征和控制性能要求相结合的特征建模思想,用简单低阶控制器实现满足控制性能指标的目标。针对一类复杂的高阶对象或者非线性系统,考虑位置保持或者跟踪的控制要求,特征模型可以用二阶或者一阶时变差分方程描述[15]。基于特征建模的黄金分割控制在满足增益约束条件下,保证了二阶差分特征模型参数未知情况下的反馈稳定性问题,解决了一般自适应控制在启动和过渡阶段参数未收敛所遇到的控制难点,设计简单,参数鲁棒性好[16]。但基于特征模型的黄金分割控制器所针对的对象模型没有考虑执行器存在饱和的情况。当不考虑执行器饱和现象,常规设计的控制器在执行器发生饱和时将会导致控制性能变差或者闭环系统不稳定。
本文提出将基于特征建模的黄金分割控制和MRAW抗饱和策略相结合的抗饱和控制方法。针对传统MRAW抗饱和方法难以处理高阶对象或者非线性对象的问题,利用二阶差分特征模型的简洁形式,以及具有在同样控制输入作用下,对象特征模型和实际对象在输出上是等价的、在稳定情况下输出是相等的等优点,在抗饱和设计中用二阶特征模型取代原被控对象,求解抗饱和补偿器中的反馈增益。将传统的离散线性MRAW抗饱和策略推广到一类高阶对象和非线性系统中,扩展了其应用范围,简化了这类系统抗饱和补偿器设计,可以更好地应用于工程实践。
1 问题描述
1.1 系统定义
根据特征建模理论,工程中常见的线性定常高阶对象式(1),以及飞行器姿态动力学方程中常用到的一类相对阶为2的单输入单输出最小相位非线性系统式(2),在满足一定采样周期的条件下,当要实现位置保持或位置跟踪控制时,其特征模型可以用一个二阶时变差分方程式(3)描述。
(1)
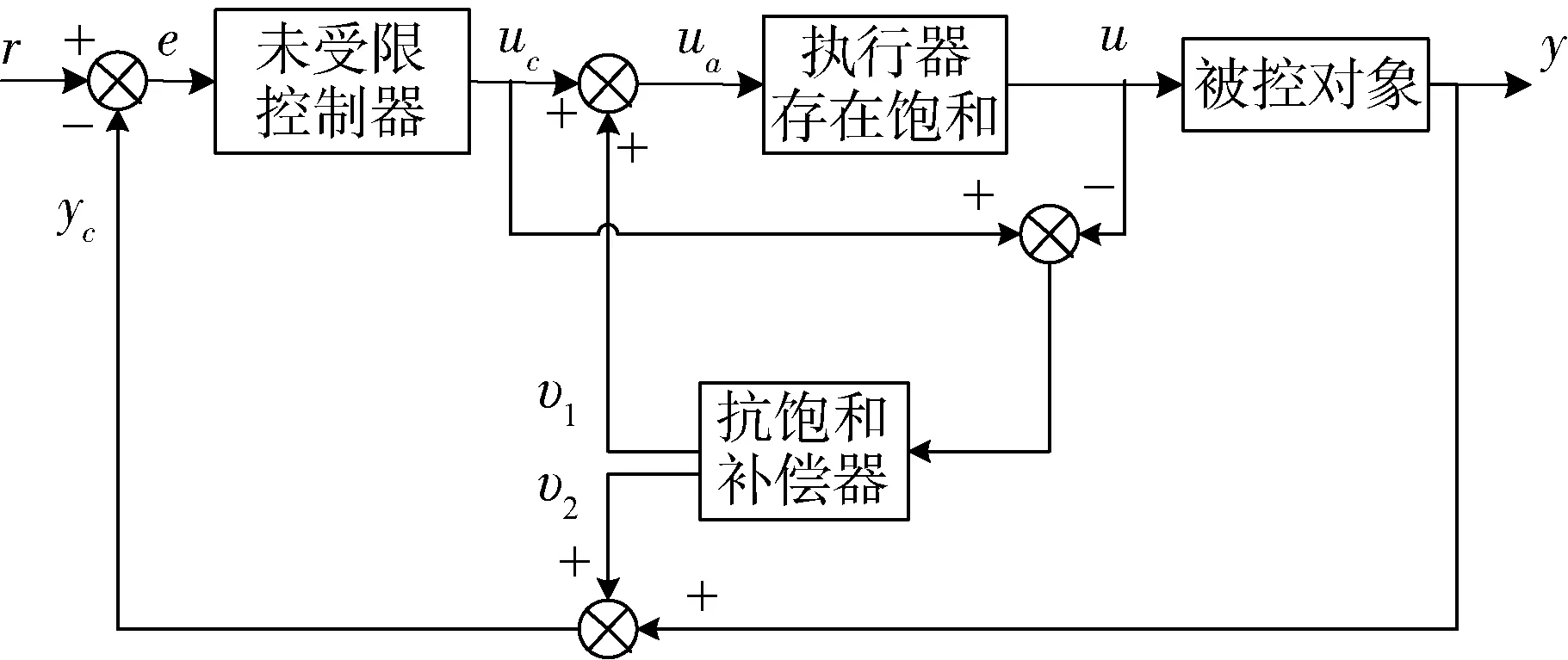
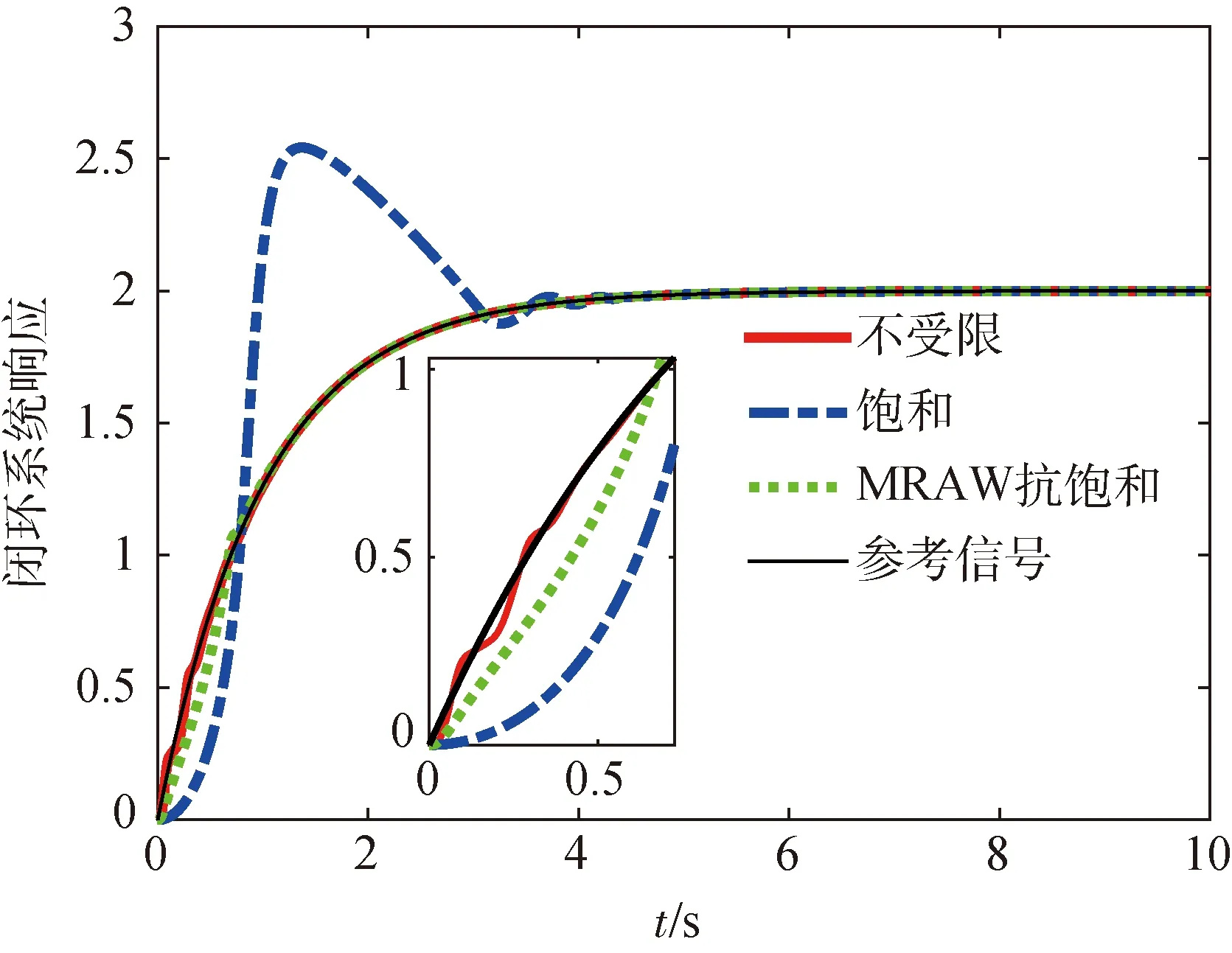
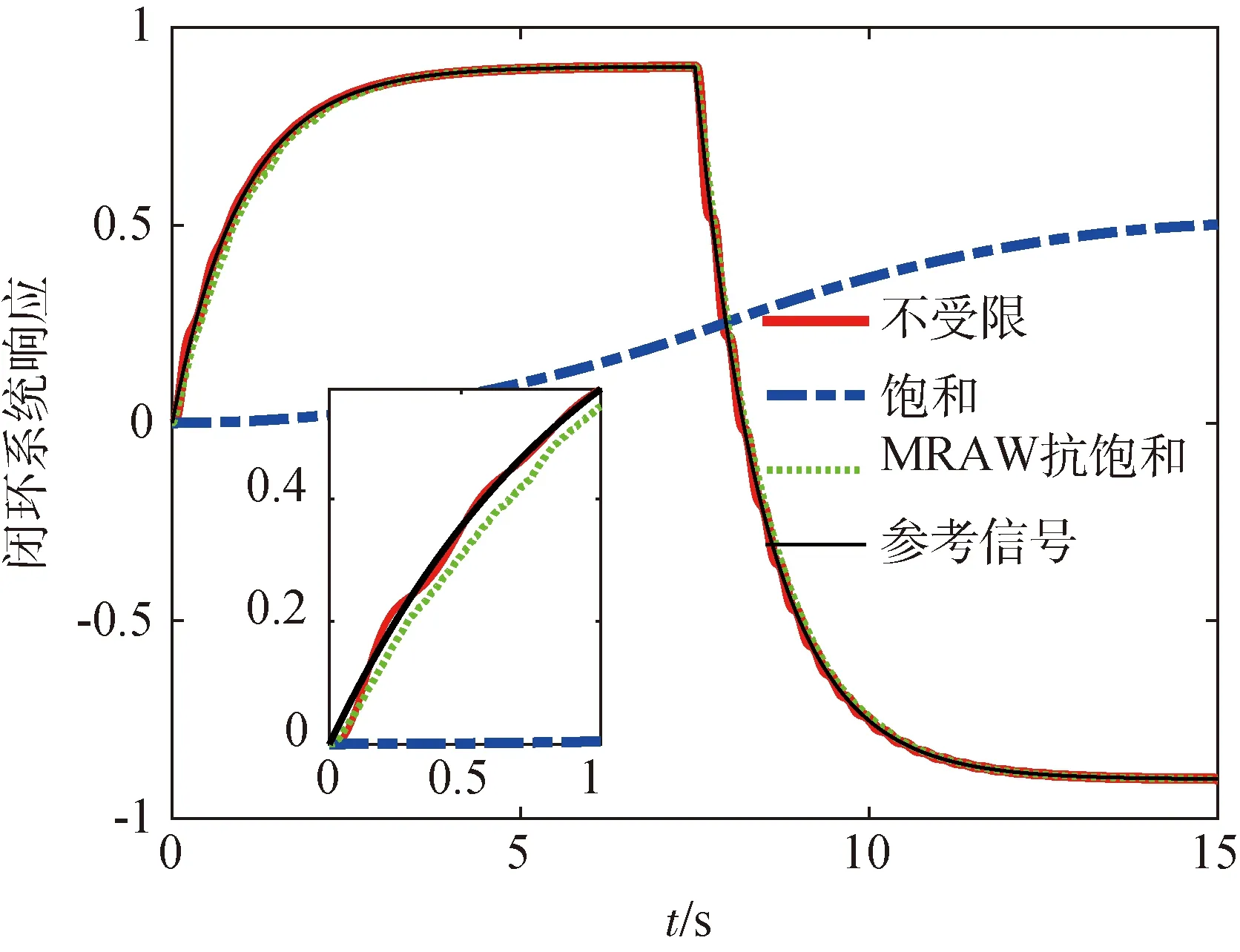
其中ai(i=0,1,…,n-1),bj(j=0,1,…,m)是定常的系统参数,m,n(m (2) 其中,x=[x1,x2]T∈R2,z∈Rm是系统的状态变量,并且x和z分别对应系统的外动态和内动态;u∈R是系统的控制输入,y∈R是系统的量测输出;a(x,z),b(x,z)和f0(x,z)均为系统的不确知非线性函数。 y(k+1)=f1(k)y(k)+f2(k)y(k-1)+g0(k)u(k) (3) 其中,y(k+1)为特征模型输出特征变量;y(k),y(k-1)是系统输出特征变量,也是系统实际输出变量;u(k)为系统输入控制特征变量,也是实际对象输入控制变量;f1(k),f2(k)和g0(k)为特征模型的特征参量,其范围可事先确定,并且在已知闭凸集内[15]。 基于特征模型的自适应控制器设计,在建立对象的特征模型后,需要对特征模型参数即特征参量进行在线估计。记特征模型参数向量 θ(k)=[f1(k)f2(k)g0(k)]T 数据向量 φ(k)=[y(k)y(k-1)u(k)]T 则特征模型(3)可记为 y(k+1)=θT(k)φ(k) (4) 参数辨识的梯度投影算法为 (5) 参考文献[15]中定理8.4和定理9.5,对系统设计自适应黄金分割控制器式(6),作为系统控制输入未受限时的标称控制器,可以保证闭环系统稳定并满足性能要求。 u(k+1)= (6) 式中,l1=0.382,l2=0.618,e(k)=y(k)-yr(k),yr(k)为参考输入。 令xp(k+1)≜[y(k)y(k+1)]T,则可将特征模型式(3)写成状态空间形式: (7) 其中, 当被控对象的控制输入存在饱和非线性时,也就是控制输入满足 (8) 需要设计合适的模型恢复抗饱和补偿器,用于补偿闭环系统发生饱和时的控制输入以及系统输出,保证发生饱和时闭环系统的控制性能和稳定性。 模型恢复抗饱和是指,从不存在控制输入饱和约束的控制器角度看,设计的抗饱和补偿器恢复了不存在控制输入饱和的系统模型。根据抗饱和设计流程,首先设计的标称控制器在不存在控制输入饱和约束时,闭环系统输出可以很好地跟踪输入指令信号,也就是具有良好的动态输出响应性能。由此可以知道存在控制输入饱和约束的抗饱和闭环控制系统在有约束的情况下应该如何响应。通过完全复制被控对象模型,MRAW抗饱和补偿器使饱和系统的闭环响应和未饱和系统闭环响应尽可能相同。 常用的MRAW方法框图如图1所示。 图1 MRAW控制结构框图 在处理高阶对象或者非线性对象时,MRAW方法同样是复制此类模型,设计复杂度却大大增加。 根据抗饱和设计流程,首先设计不考虑控制输入饱和的基于特征模型的自适应黄金分割控制器,可以得到稳态时的特征模型。根据特征建模理论,在稳定情况下,对象特征模型和实际对象在输出上是相等的。因而可以在MRAW中使用稳态特征模型取代原被控对象来求解抗饱和补偿器,用线性MRAW抗饱和方法实现高阶对象或者非线性对象的抗饱和设计。 稳态时对象特征模型记为 (9) 其中, 这种补偿器的设计可以归结为构造一个状态反馈控制器,可以使饱和系统的响应趋向于期望的响应。设计如式(10)的模型恢复抗饱和补偿器,用于补偿闭环系统发生饱和时的控制输入,整个闭环系统框图如图2所示。 图2 基于特征模型的模型恢复抗饱和控制框图 (10) 上述抗饱和补偿器的输入为执行器输出与输入之差,输出分别为补偿信号υ1和υ2。补偿信号υ1使用抗饱和补偿器的状态通过修正控制器的控制输出来恢复系统退出饱和时的性能;而补偿信号υ2通过修正被控对象输出反馈,补偿由于控制量饱和引起的输出损失,衡量饱和状态下闭环系统实际输出与不存在执行器饱和的理想输出之间的偏差。因而需要选取合适的抗饱和增益K,使υ2尽可能小以获取较好的跟踪性能,且闭环系统稳定。 由控制结构图2可知,存在式(11)和(12)约束 u(k)=sat(ua(k))=sat(uc(k)+υ1(k)) (11) yc(k)=y(k)+υ2(k) (12) 为了分析包含抗饱和补偿器的闭环系统稳定性和性能,定义状态变量ζ(k)=xp(k)+xaw(k),系统输出ζ(k)=y(k)+υ2(k),因而由式(7)和式(10)可以得到包含抗饱和补偿器的闭环系统的状态方程 (13) 下面分析系统(13)的内稳定性,给定渐进稳定的被控对象,只要保证饱和函数和抗饱和补偿器组成的部分是稳定的,那么包含抗饱和补偿器的整个闭环系统就是稳定的。 定理1 给定不存在饱和约束的稳定闭环系统和设计好的抗饱和增益K,如果存在,P=PT>0,W=WT>0使得下述矩阵不等式成立,那么饱和函数和抗饱和补偿器组成的部分从输入uc到状态xaw是l2稳定的。 (14) 证明: 1)扇形饱和函数约束条件 (15) 由式(11)知,ua,k=uc,k+υ1,k=uc,k+Kxaw,k,代入到式(15),可得 (16) 2)l2稳定性证明 (17) 考虑饱和非线性式(16),代入式(17),可得 (18) 由线性矩阵不等式(14)可知,存在足够小的ε>0,使得下式成立 因而存在 (19) 对式(19)采用完全平方变换,可得 (20) 由式(20)容易得到 (21) 因而存在足够大的γ>0,使得式(22)成立 (22) 将式(22)两边从0到∞相加,可以得到 (23) 由于Lyapunov函数V(xaw,∞)≥0,可知 (24) 因而函数和抗饱和补偿器组成的部分从输入uc,k到状态xaw,k是l2稳定的 3)转化为线性矩阵不等式 式(14)是非线性矩阵不等式,可以通过Schur补引理和等价变换转化成容易求解的线性矩阵不等式。 由式(14)可得 (25) 式(25)用Schur补可得 (26) 式(26)左右同时乘以对角阵diag(I,P-1,W-1),可得 (27) 令Q=P-1,U=W-1,Ω=KQ,则式(27)可以写成 (28) 因而式(14)的矩阵不等式可以转化为式(28)的线性矩阵不等式,证毕。 前述分析了给定抗饱和补偿增益K,由整个闭环系统的内稳定性,可知求解下述的可行性线性矩阵不等式,即可求得抗饱和补偿增益。 Q=QT>0,U=UT>0,Ω=KQ,γ>0。 (29) 考虑被控对象 跟踪参考输入yr=2,控制输入限制M=1,采样周期T=0.005s。 设计自适应黄金分割控制器,然后根据设计的黄金分割自适应控制器,设计线性MRAW模型恢复抗饱和补偿器,所求的抗饱和增益K=[0.0308-0.0334]。 因而所求解的MRAW抗饱和补偿器为 控制结果如图3所示。不存在控制输入饱和时,所设计的自适应黄金分割控制器经过较短时间的调整,能使系统输出较好的跟踪参考信号,当存在控制输入限制时可以看到控制性能急剧变差,此时加上MRAW抗饱和补偿器之后,系统能够重新很好地跟踪参考信号,通过局部放大图可以看到,存在抗饱和补偿器时的闭环系统瞬态响应较不受限系统有一定的提升。可知针对此非线性系统,设计自适应黄金分割控制器,进而基于特征模型设计线性MRAW抗饱和补偿器,可以实现执行器饱和时的控制性能恢复。 图3 闭环系统响应 文献[17]中的被控对象是带有对称挠性帆板卫星的俯仰轴动力学的简化模型: 其中,J为卫星转动惯量,ω为俯仰角速度,Tt为控制力矩,G=[g1g2]T,为挠性模态与卫星俯仰运动的耦合系数矩阵,q=[q1q2]T为模态坐标,Λ=diag(Λ1,Λ2),为约束模态频率。 采样时间0.005s,模型参数: J=3732kg·m2 Λ1=Λ2=diag(0.1979,0.7000,1.2087)×2π 跟踪通过低通滤波器的方波信号,控制输入限制M=30,同样先设计自适应黄金分割控制器,可以满足不存在输入饱和时的控制要求,进而设计MRAW抗饱和补偿器。 控制结果如图4所示,可以看到采用MRAW抗饱和补偿器之后,系统闭环响应可以较好地跟踪参考信号,但是在调整阶段还是存在一定的性能损失。 图4 带有挠性帆板的卫星俯仰轴响应 设计了将基于特征建模的黄金分割控制和MRAW抗饱和策略相结合的抗饱和控制方法。针对传统MRAW抗饱和方法难以处理高阶对象或者非线性对象的问题,利用二阶差分特征模型的简洁形式,以及具有在同样输入控制作用下,对象特征模型和实际对象在输出上是等价的,在稳定情况下输出是相等的等优点。在抗饱和设计中用二阶特征模型取代原被控对象,求解抗饱和补偿器中的反馈增益。这样就将传统的离散MRAW抗饱和策略推广到一类高阶对象和非线性系统中,扩展了其应用范围,简化了这类系统抗饱和补偿器设计,可以更好地应用于工程实践。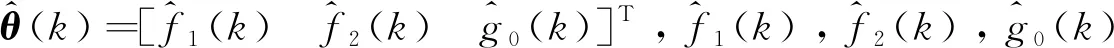
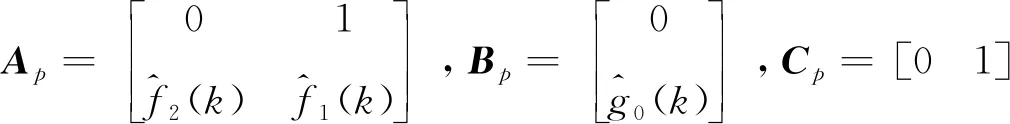
1.2 模型恢复抗饱和设计
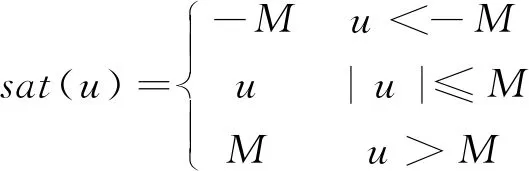
2 基于特征建模的MRAW方法
2.1 线性MRAW设计

2.2 稳定性分析
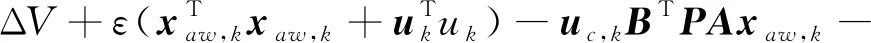
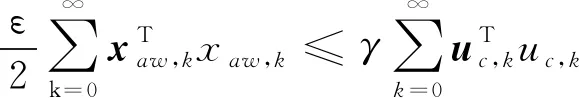
3 仿真校验
3.1 非线性对象
3.2 带有挠性帆板的卫星俯仰轴控制
4 结 论
