适合一类动目标插拔操作的机械臂变阻抗控制方法

张玲俊 刘 磊,2 王 勇,2

1. 北京控制工程研究所，北京 100190 2.空间智能控制技术重点实验室，北京 100190

0 引言

航天器在轨服务是指在空间通过人、机器人或两者协同完成涉及延长各种航天器寿命、提升执行能力的一类空间操作[1-2]。机械插拔是在轨服务的重要操作形式，广泛应用于失效模块的维修和更换、精细组装以及在轨加注等。对于精细插拔操作任务，在手眼相机引导机械臂末端接插件与插座接触后，视觉由于受到遮挡不能继续提供有效的测量信息，机械臂需要完成盲插拔操作。在许多工程问题中，特别是在机械臂的位姿存在误差或目标测量不准确的情况下，插拔操作不可避免地与环境存在接触。此时，由于环境的约束，采用单纯的位置控制会因为机械臂末端微小的位姿偏差失去接触或产生巨大的接触力，这将直接影响操作任务的完成，并且极有可能损坏环境或损伤机械臂。因此，需要引入力反馈，通过柔顺控制使机械臂具有柔顺性。柔顺性(也称顺应性)是指能够对外界接触环境变化顺从的适应能力[3-4]。柔顺控制分为被动柔顺控制和主动柔顺控制。相较于由机械装置产生的被动柔顺控制，主动柔顺控制是通过设计适当的控制器使整个系统呈现所需的表观惯性、表观阻尼和表观刚度，以达到柔顺交互的目的。

根据系统的因果关系，主动柔顺控制的实现方式分为阻抗控制和导纳控制[5]。很多学者针对机械臂动力学模型不确定、环境刚度未知或变化的问题以及在插拔操作过程中存在的其它实际应用问题进行了大量研究。文献[6-9]关注于机械臂动力学系统模型的不确定问题。当环境刚度存在较大变化时，Christian Ott等[9]提出统一导纳控制和阻抗控制的控制策略。Seul Jung[10]等将环境建模为固定刚度的弹簧，由环境位置和交互力求解环境刚度，以此解决环境刚度未知的问题。廖琳静[11]提出基于反馈位置和基于控制时间的两种修正因子模型，解决了只通过调节参数不能同时满足较小稳态误差和超调量的问题。董悫[12]提出了一种虚拟弹簧平衡位置可变的控制方法，解决了虚拟弹簧项所产生的阻抗力影响系统稳定的问题。针对形状特征和位置未知的交互环境，段星光等[13]基于阻抗控制建立了安全空间以及安全姿态角的运动约束。DuanJinjun等[14]提出了一种自适应变阻抗控制方法调整阻尼参数，使机械臂在斜坡和复杂表面上运动时力跟踪误差达到预期的效果。但是，上述文献对操作对象(或称为环境)存在不确知动态变化的关注较少。

空间机械臂在进行空间操作的过程中，服务星先通过对接与目标星固连为一个整体，然后再进行插拔操作。但是由于服务星与目标星之间锁紧装置刚度不够等原因，意外扰动将引起目标星(含插座)和服务星(含机械臂及接插件)之间出现相对运动，并且相对运动状态不确知。这时，插拔对象不再静止，而是一个运动状态不确定的动态系统。相比于插座运动状态确知的插拔过程，动目标盲插拔存在两个主要问题：1)在插拔操作的法线方向上，插座相对于机械臂末端存在不确知的相对运动，导致机械臂末端受到较大的接触力或失去接触，需要控制机械臂末端保持与插座的柔顺随动，称为不确知动目标的柔顺跟随问题；2)在插拔操作的方向上，插座位置固定但不确知，机械臂与插座底部的碰撞会带来反复刚性跳动问题，导致在插座底部机械臂末端长时间不能稳定，需要控制机械臂末端与插座底部实现快速稳定接触，称为插座底部反复碰撞问题。

为了使机械臂与具有不确知运动的插座交互时具有柔顺行为，阻抗参数需要随插座运动状态的动态变化而变化。在大多数情况下交互作用力可以表征交互过程的特性，因此通常根据力觉测量信息动态调整阻抗参数，主要有1)构造函数方法，比如文献[15]。2)自适应方法，比如文献[14]和[16-17]；3)智能调节方法，比如基于路径积分的改进策略算法(Policy Improvement with Path Integrals，PI2)[18]、概率推理学习控制算法(PILCO)[19]等强化学习算法；4)类人/仿人方法，比如通过阻抗学习(Impedance Learning)迭代地调节机械臂期望的刚度、阻尼矩阵以获得期望的阻抗模型[7]，以及在康复机器人相关领域的许多研究者比如肖志业[20]开展了将人的运动控制技能向机器人传递的研究。

结合现有阻抗控制及变阻抗算法相关的思想，本文开展了适用于插座运动状态不确知的盲插孔操作的变阻抗控制方法研究。针对不确知动目标的柔顺跟随问题和插座底部反复碰撞问题，本文分别提出了变阻抗柔顺随动控制算法和变阻抗稳定接触控制算法，实时调节阻抗参数，并通过了实验验证，未来可用于空间不确知动态插拔对象的精细插拔等操作任务。

1 阻抗模型建立

Hogan基于“不可能设计一种控制器使物理系统在环境中呈现出与纯粹物理系统不同的行为”的假设，使用等效物理系统描述整个受控系统，提出了两个动态交互系统在物理上必须互补的结论[5]。因此，为了避免因果冲突，在任意一个自由度上，当环境表示为导纳时，应使整个机械臂系统具有阻抗特性，反之亦然。

完整机械臂系统(包含硬件和软件)是非线性系统，运动变量和力变量之间具有不可逆的因果约束关系，阻抗和导纳是系统不可互换的特性表示[14]。存在不确知运动的可移动插座具有受运动约束的惯性物体的性质：以交互力为输入来确定相应的运动响应，所以具有导纳特性，故而被控机械臂整体应该具有阻抗特性。很显然，基于阻抗控制的整个机械臂系统满足阻抗特性(输入是期望位姿等运动量，输出是力/力矩)，从而保证与导纳特性环境的物理兼容性。

机械臂末端接插件和插座之间的交互作用模型很难找到确切的显式表达或找到确切关系，建立之后也难以准确地实现参数辨识，所以需要将机械臂末端建立为阻抗模型来解决这一问题。阻抗模型通常采用二阶的形式，简化为一端固定的“质量——阻尼——弹簧”系统，如图2所示。

图1 阻抗和导纳示意图

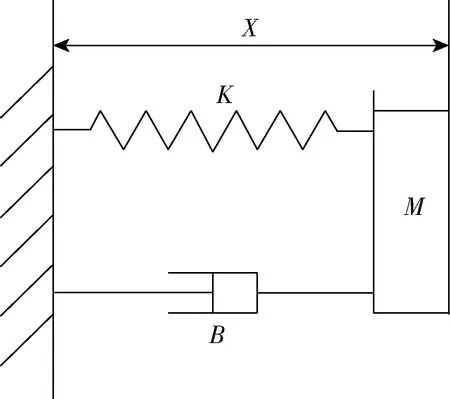
图2 阻抗模型

数学模型为

(1)

2 变阻抗控制器设计

图3 阻抗控制结构图

通常将阻抗参数设定为对角正定矩阵以实现机械臂在笛卡尔空间中各个坐标轴方向的解耦控制。因此，可以不失一般性地只分析其中一个自由度，令fd、fe、m、k、b分别表示Fd、Fe、M、B、K中的元素，由式(1)可得闭环系统方程为

(2)

式中，e=x-xd。

由于插座刚度很大，可以将其简化为一个刚度为ke的线性弹簧，插座的初始位置用xe表示。因此，机械臂末端与环境的接触力为

fe=ke(xe-x)

(3)

由式(2)可以写出闭环系统传递函数为

(4)

由于底层关节空间的控制可以达到很高的精度，分析时认为输入和输出的位置、速度和加速度一样。因此，将式(3)代入式(2)，考虑到式(4)，力误差可以表示为

(5)

当机械臂末端与插座之间交互达到稳态时，力稳态误差为

(6)

由式(6)可以得出稳态时力跟踪误差为0需要满足的条件是xd=xe-fd/ke或k=0。由于环境的刚度ke和初始位置xe无法准确估计，这里选择将刚度参数设置为k=0，于是有

(7)

此时，机械臂末端阻抗模型可等效为质量-阻尼系统。

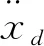
(8)

实际应用的时候将连续的闭环系统方程式(8)离散化，改写为：

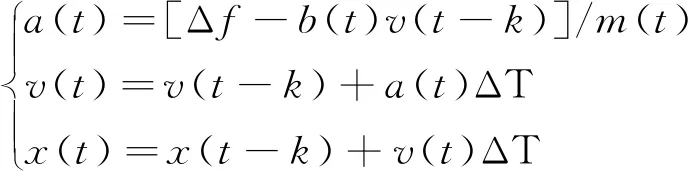
(9)

其中，x、v、a分别表示机械臂末端的位置、速度和加速度，ΔT是机械臂控制器的控制周期，k是控制器的采样周期。

2.1 变阻抗柔顺随动控制算法

机械臂柔顺跟随不确知运动插座的控制目标是使机械臂末端快速跟随插座运动，且将二者之间的接触力控制在指定范围以内。机械臂末端跟随插座的不确知运动的效果越好，二者之间的接触力越小，理想的跟随效果是机械臂不改变插座运动状态且能柔顺跟随插座运动。阻抗参数调节的难点在于大阻抗参数使得机械臂系统稳定但不够柔顺；小阻抗参数使得机械臂系统柔顺但不够稳定。

本文研究的重点不是寻孔，因此设定初始状态为机械臂末端的接插件和插座的孔壁已经接触。由于盲跟随不确知运动的过程中容易丢失插座的位置，所以设定接插件与插座之间保持恒定期望接触力fd随动。

存在不确知动态变化的插座运动可以简化为方向、幅值、频率单一变化的叠加。因此，按照时间序列依次取一定的时间间隔可以将插座不确知运动状态分割成多个局部静止状态的集合。很显然，当插座没有对接插件施加作用力时，机械臂末端是大阻尼才能使机械臂具有更强的稳定性；当目标插座相对接插件运动并向其施加接触力时，机械臂末端是小阻尼才能柔顺跟随。所以，当插座的运动参数是时间的函数时，只有阻抗参数也随之连续变化才能更好地柔顺随动。

将式(8)中的b修改为b+Δb，于是变阻抗柔顺随动控制的闭环系统方程为

(10)

将式(10)离散化后，可得

(11)

由于插座运动状态不确知，故只考虑实际接触力的大小而不考虑方向。为了实现柔顺跟随效果，当fd>0时，具体的阻尼参数的调节方法为

Δb(t)=δ(fd-|fe(t-k)|)

(12)

式中，δ是更新系数，k是控制器的采样周期。

由式(11)和式(12)可知，阻尼参数在实际接触力为0的时最大，为b+δfd。当环境施加给机械臂作用力小于期望作用力时，机械臂的阻尼较大，以恒定接触力与插座壁面一侧保持接触，二者相对静止；当环境施加给机械臂的作用力大于期望接触力且方向相同时，或者环境施加给机械臂一个与期望接触力反方向的作用力时，不管接触力的幅值大或小都可以快速响应并柔顺跟随。

2.2 变阻抗稳定接触控制算法

在接近插座底部的过程，机械臂同时具有自由空间和接触空间的运动，在与插座底部交互过程中存在反复碰撞问题。难点在于，固定参数的阻抗控制策略不能有效解决从自由空间运动突变为接触运动时存在的反复碰撞问题。在同样的期望作用力牵引下，如果选择较小的质量和阻尼参数，插拔速度快，非常柔顺，但难以与插座稳定接触，反复碰撞问题显著；如果选择较大的质量和阻尼参数，插拔速度慢，碰撞产生的力峰值小，但是反复碰撞问题依然存在。本文提出的变阻抗稳定接触控制算法包含机械臂接近插座底部过程中自由空间的控制和末端与插座底部接触后的接触空间的控制，且在两种空间里控制策略无需切换，实现了机械臂无论在自由空间运动还是接触空间运动时力和运动都能综合控制，可以适应插座位置在插拔操作的方向上固定但具有不确性的插拔操作。

当机械臂在自由空间运动时，实际接触力fd为0，期望接触力fd可以视为“虚拟力”，机械臂在-fd的驱动下运动。假设机械臂末端在初始时刻静止，对式(8)进行求解可得

(13)

(14)

由式(13)和式(14)可知，在期望接触力fe的作用下，机械臂末端在自由空间的运动速度的大小随着时间增加单调递增，而加速度的大小随时间增加单调递减。如果惯性参数和阻抗参数固定不变的话，力与运动之间的关系是不变的。只要存在由接触空间运动不断切换为自由空间运动的情况，经过一段时间之后，机械臂末端总会以较大的速度反复撞击插座底部。这也表明，只设定一个期望接触力不能满足机械臂末端与插座底部快速稳定接触的插拔任务要求。

为了解决机械臂末端夹持固定的接插件与插座底部接触之后既难以稳定接触也不能最终收敛到期望的接触力这个问题，设定一个随接触力超过阈值而不断累积计数的计数器count，并令速度和加速度随count累积同比降低，所以具体的阻抗参数的调节方法如下

(15)

式中，k为控制器的控制周期，gm和gb分别为惯性惩罚系数和阻尼惩罚系数。随着惩罚项增加，惯性参数和阻尼参数都相应地增加一定的幅度。这意味着在下一次控制周期将以更低的加速度和速度从自由空间切换为接触空间，最终使得加速度、速度、位置的修正量为0，从而达到快速稳定接触的目标。

3 实验验证

3.1 实验条件

简化实际接插件和插座的真实复杂结构为零件和安装孔(直孔)。物理实验系统主要由六自由度的UR10机械臂、六维力/力矩传感器、零件、安装孔、工控机等组成，如图4所示。UR10机械臂有位置和速度2种运动控制模式，考虑到运动的快速性和轨迹的光滑性，选择了速度控制模式。

图4 物理实验装置图

在插拔操作过程中，由安装在机械臂手腕处六维力/力矩传感器检测机械臂末端与插座接触状态的变化。通过力/力矩传感器可以获得沿传感器坐标系3个坐标轴方向的力矢量的3个分量和绕传感器坐标系3个坐标轴方向的力矩矢量的3个分量，将其转化为机械臂末端工具坐标系下的分量表示为

F=[fxfyfzτxτyτz]T

(16)

在后续实验中实际接触力用式(16)表示，UR10机械臂的工具坐标系选择默认设置：以工具中心点(TCP)为原点，沿最后一个关节的轴向方向为z轴。控制器的控制周期设为ΔT=0.04s，控制器每运行一次进行一次采样并保存实验数据，所有实验结果图的横坐标为采样点。

3.2 实验结果

3.2.1 验证变阻抗柔顺随动控制算法

本小节通过“变阻抗柔顺随动实验”来验证变阻抗柔顺随动控制算法是否解决了不确知动目标的柔顺跟随问题，并且借助安装孔运动相同以比较接触力大小和接触力不变以比较跟随运动两组“固定阻抗随动实验”，分析本文所提出的变阻抗柔顺随动控制算法相比于固定阻抗随动算法带来的柔顺性能提升。安装孔模拟往复运动，以工具坐标系y轴方向为例进行实验验证。

(1)变阻抗柔顺随动实验

按照式(11)和式(12)进行“变阻抗柔顺随动实验”，设定惯性参数m为0.1，阻尼参数的初始值b为1.5，更新系数δ为100，期望接触力fd为3N，实验效果为图5～7。

结合图5～7分析，从第127个采样点到第164个采样点，实际接触力fe>3N，阻尼参数b+Δb随接触力减小，机械臂末端实现了沿工具坐标系y轴负方向的跟随运动；从第203个采样点到第252个采样点，实际接触力fe<-3N，阻尼参数b+Δb随接触力减小，机械臂末端实现了沿工具坐标系y轴正方向的跟随运动；从第284采样点到第307个采样点，实际接触力fe>3N，阻尼参数b+Δb随接触力减小，机械臂末端再次实现了沿工具坐标系y轴负方向的跟随运动；从第308个采样点到第321个采样点，实际接触力fe为0，阻尼参数修正量Δb在0.3附近，阻尼参数b+Δb增加，此时机械臂基本静止。

对比图5和图6发现，阻尼参数修正量Δb根据期望力fd和实际接触力绝对值|fe|的差值进行实时修正。通过图5和图7可知，机械臂可以良好跟随速度介于±0.05m/s之间的安装孔运动，接触力可以控制在±20N的范围以内。

图5 机械臂沿工具坐标系y轴的实际接触力

图6 沿工具坐标系y轴的阻尼参数修正量Δb

图7 机械臂末端在工具坐标系下的加速度、速度和位置

(2)固定阻抗随动实验

首先，进行第一组固定阻抗随动的对比实验，保持安装孔运动方向、幅值、频率与第一组实验相同，以比较零件与安装孔之间的接触力大小。设置期望接触力fd为3N，惯性参数为0.1，阻尼参数为1.5，并保持不变，实验结果为图8和图9。

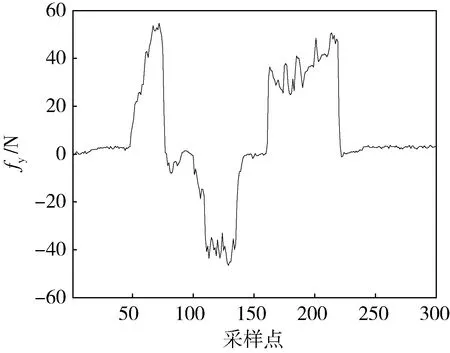
图8 机械臂沿工具坐标系y轴的实际接触力

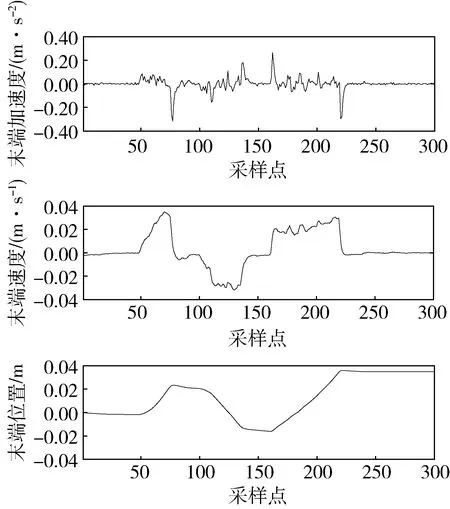
图9 机械臂末端在工具坐标系下的加速度、速度和位置

与图5相比，图8中沿机械臂末端工具坐标系y轴的传感器读数明显增大，比如在第73个采样点实际接触力的峰值高达54.7N，约为变阻抗控制时接触力大小的3倍。这表明在相同运动的情况下，变阻抗柔顺随动算法可将接触力控制在更低范围，明显优于固定阻抗随动效果。

然后，进行第二组固定阻抗随动的对比实验，保持接触力大小不变以比较安装孔跟随运动。设置期望接触力fd为3N，惯性参数为0.1，阻尼参数为1.5，并保持不变，实验效果为图10和图11。

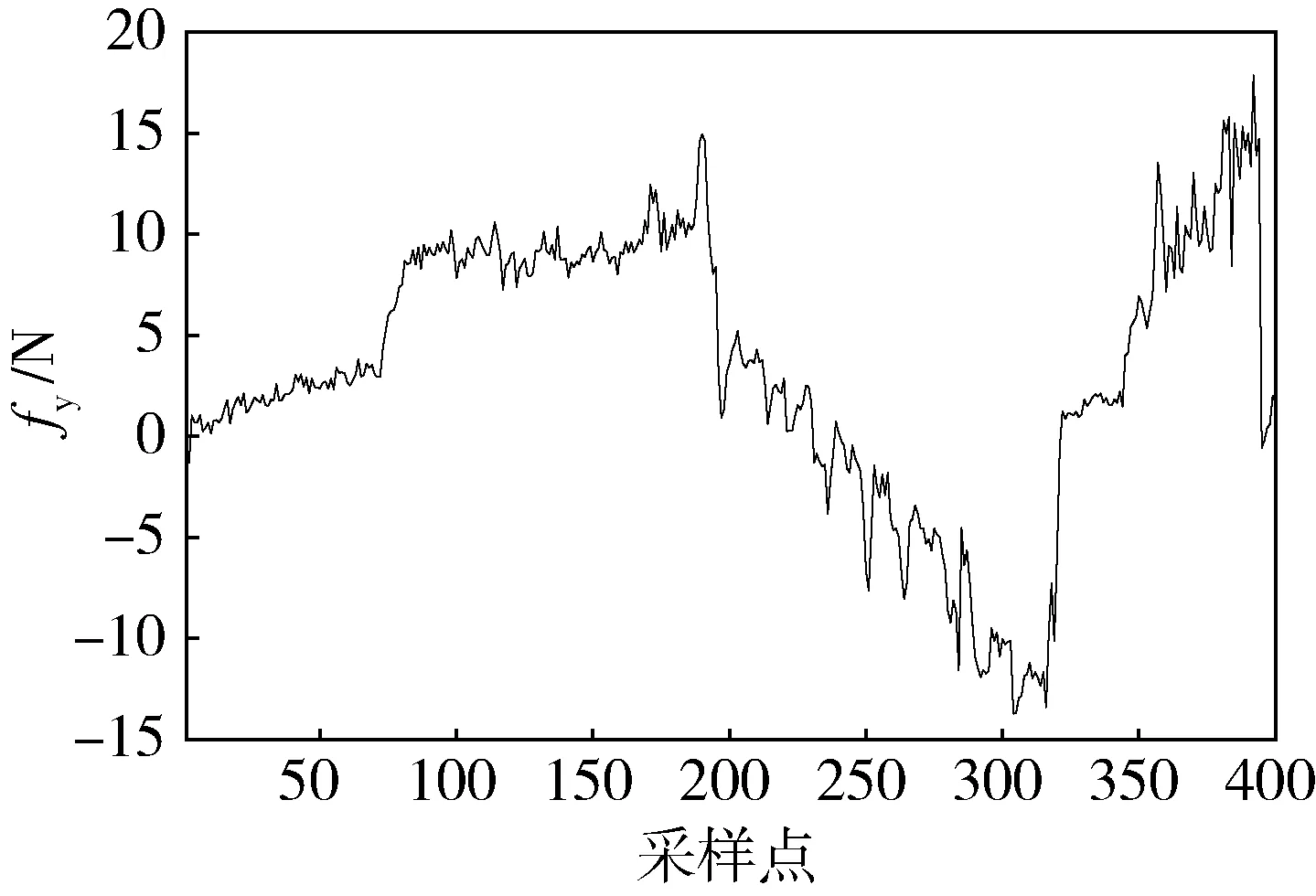
图10 机械臂沿工具坐标系y轴的实际接触力

图11 机械臂末端在工具坐标系下的加速度、速度和位置

虽然图5和图10接触力变化的峰值均在±20N的范围以内，但是相比于图6，图11中安装孔运动速度在±0.01m/s，约为变阻抗柔顺随动实验可以跟随的速度大小的1/5。这表明如果将接触力控制在相同的范围，变阻抗柔顺随动算法可以跟随更快速度的安装孔运动，其随动效果明显优于固定阻抗随动算法。

3.2.2 验证变阻抗稳定接触算法

本小节通过“变阻抗接触实验”验证变阻抗稳定接触算法是否解决了机械臂与插座底部接触后的反复碰撞问题并验证所提出算法的适应性，借助“变阻抗接触实验”与“固定阻抗接触实验”对比分析本文提出的变阻抗稳定接触算法带来的性能提升。以工具坐标系z轴方向为例进行实验。

(1)变阻抗接触实验

按照式(9)和式(15)进行变阻抗稳定接触控制算法的验证实验，设定期望接触力为8N，初始的惯性参数为0.1，初始的阻尼参数为1.5，gm=0.1，gb=1.5，实验效果为图12～14。

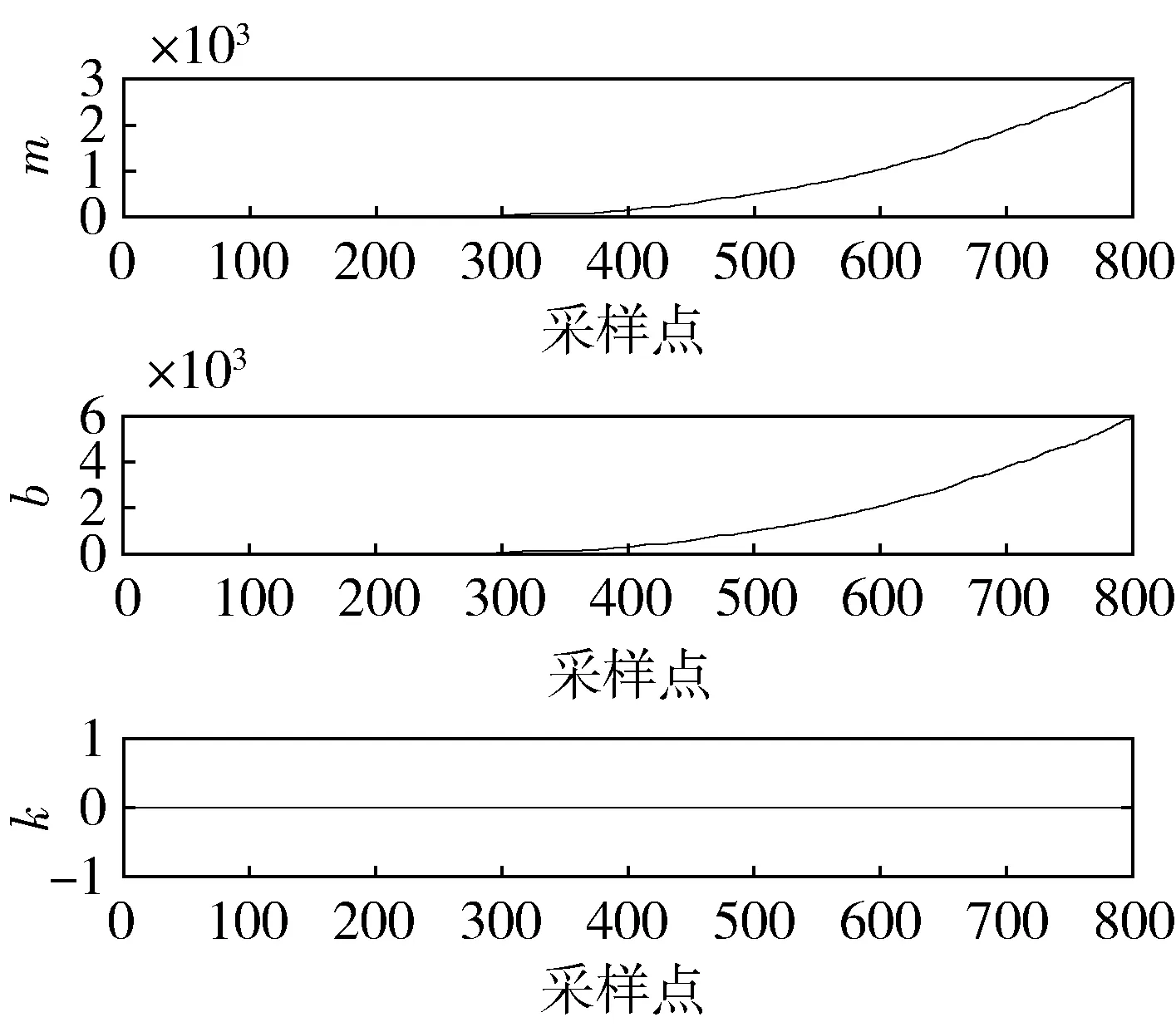
图12 阻抗参数变化情况

图12说明在插拔实验中，惯性参数m(t)和阻尼参数b(t)随着接触力超过设定阈值次数count的增加而逐渐增加。图13说明随着count的增加，当惯性参数m(t)和阻尼参数b(t)累加到一定程度时，机械臂末端的加速度和速度为0，位置不变。在图14中，虚线表示的是机械臂末端工具坐标系下的期望接触力fd，可以看出实际接触力最终稳定在期望接触力±1N范围以内。实验结果说明变阻抗稳定接触算法可以解决盲插拔操作中机械臂末端零件与安装孔底部反复碰撞问题。

图13 机械臂末端在工具坐标系下的加速度、速度和位置

图14 机械臂沿工具坐标系z轴的实际接触力

保持实验设置相同，将安装孔的位置沿插拔操作方向随机降低一定距离以进一步验证变阻抗稳定接触控制算法的适应性，实验结果为图15～17。

图15 阻抗参数变化情况

图16 机械臂末端在工具坐标系下的加速度、速度和位置

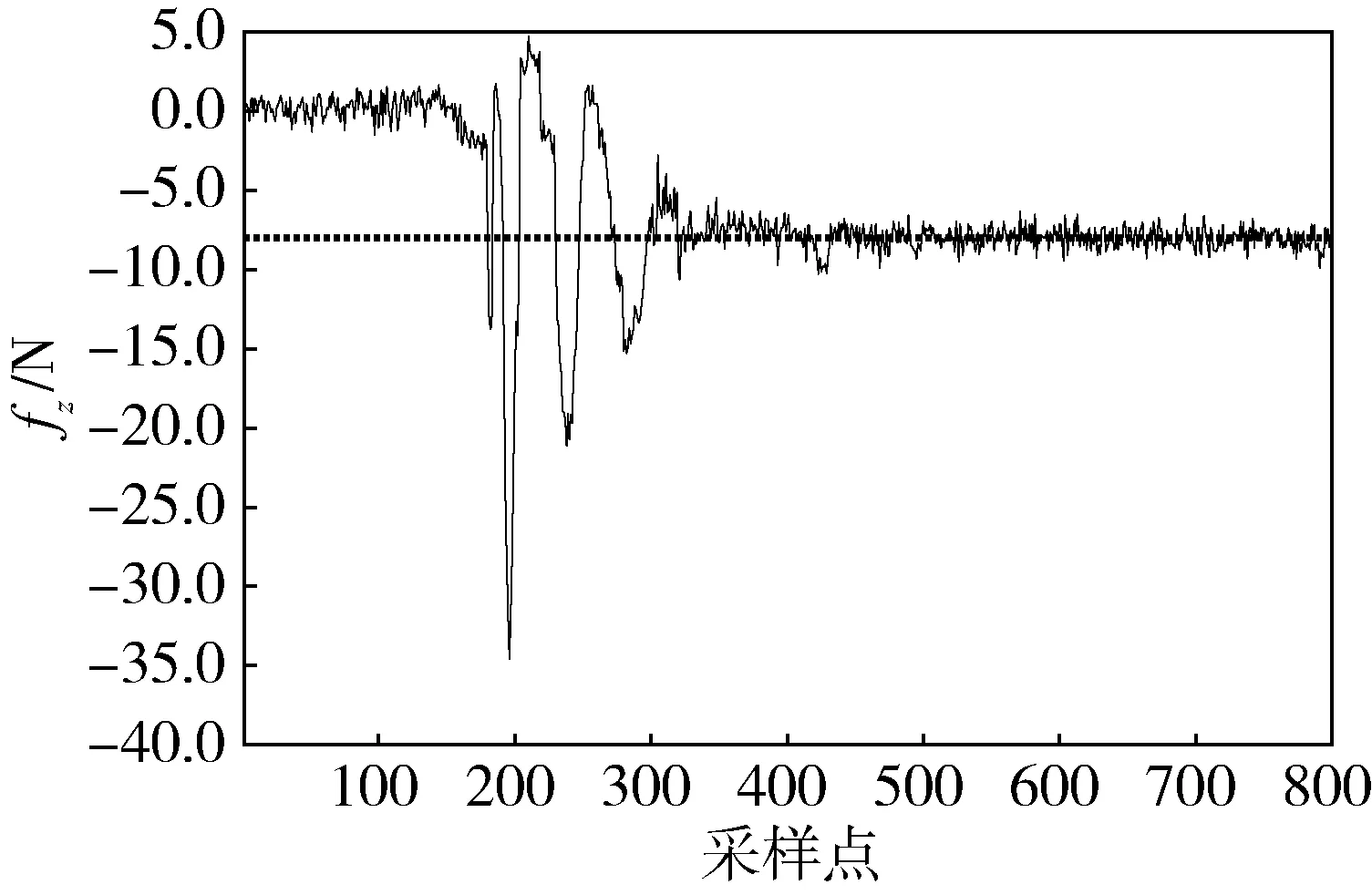
图17 机械臂沿工具坐标系z轴的实际接触力

图15～17的实验结果说明变阻抗控制策略实现了机械臂在自由空间以期望接触力为“虚拟牵引力”运动，经过孔底短暂交互调整后，在接触空间快速稳定在期望接触力范围之内。变阻抗稳定接触控制算法是在期望接触力的作用下控制机械臂运动到安装孔的底部，且可以适应插拔操作目标位置的不确知情况。

(2)固定阻抗接触实验

固定阻抗接触的对照实验设定期望接触力为8N，惯性参数为0.1，阻尼参数为1.5，实验效果见图18～19。从图18～19可以看出，机械臂初始时静止，之后在自由空间中以期望接触力为驱动力向下运动，自从接触到孔底后，频繁在接触空间和自由空间之间切换，重复碰撞——弹起的模式，实际接触力长时间难以稳定。很显然，变阻抗稳定接触算法解决了机械臂与插座底部接触后的反复碰撞问题。

图18 机械臂沿工具坐标系z轴的实际接触力

图19 机械臂末端在工具坐标系下的加速度、速度和位置

4 结论

本文将不确知的插座运动分成了沿插拔操作的法线方向和沿插拔操作的方向2种，分别针对不确知动目标盲插拔操作任务中的不确知动目标的柔顺跟随问题和插座底部反复碰撞问题进行了研究，使机械臂在未知动态变化环境中表现出良好柔顺性。首先，本文设计了变阻抗柔顺随动控制算法，根据交互作用力实时调整阻尼参数，满足了插拔过程中柔顺跟随安装孔运动的要求，将接触力控制在期望范围。其次，设计了变阻抗稳定接触控制算法，根据碰撞累计次数增加适当的惩罚项进行阻抗参数调节，使零件可以与安装孔快速稳定接触，有效解决了从自由空间运动突变为接触运动时由于碰撞导致的刚性跳动问题。

本文提出的两种变阻抗控制算法实现了在精细操作过程中阻抗参数的实时优化，使机械臂更好地适应插拔操作任务，灵活地应对环境的动态性和不确定性，其中变阻抗柔顺随动控制算法适用于不确知动目标的柔顺跟随问题，变阻抗稳定接触控制算法适用于插座底部反复碰撞问题。这两种简单的调节策略便于在真实的机械臂上使用，为未来面向空间操作的机械臂开展在轨服务提供了可行的控制方法。后续将进一步引入智能控制方法以提升不确知动目标柔顺跟随的性能，并针对柔顺跟随过程中的反复碰撞问题开展相关研究。