一种基于参数在线辨识的最优再入制导算法*
2021-11-17尤志鹏郑宏涛
尤志鹏 杨 勇 郑宏涛 刘 刚
中国运载火箭技术研究院,北京 100076
0 引言
近年来以X-37B、IXV等为代表的升力式可重复使用飞行器得到越来越广泛的关注。这种飞行器既能够实现在轨长时间运行,又能够实现水平着陆,并且具备良好的可重复使用能力,有力带动了先进制导控制等技术的发展,成为近年来的研究热点[1-2]。
良好的再入制导律设计对提升飞行性能具有显著作用。基于标准轨迹的再入制导是当前应用最广泛的升力式再入制导方法,众多学者对基于标准轨迹的再入制导算法进行了深入研究。文献[3]通过设计阻力加速度-能量参考曲线和航迹偏航角-能量参考轨迹,同时规划飞行器纵向运动和横向运动,提出衍化加速度再入制导律。可在线调整标准阻力加速度剖面,具有较强的自适应能力,可以应用于大横程再入飞行的情况。文献[4]在速度-高度剖面内设计参考轨迹,可在线预测待飞航程及飞行时间,可实现时间协同再入制导。文献[5]设计了一种基于阻力加速度倒数-能量的飞行剖面,利用三次样条描述阻力加速度倒数剖面并周期性更新,具有良好的工程应用潜力。文献[6]设计了一种通过跟踪阻力加速度-能量剖面,并在末端引入航迹倾角控制实现航迹倾角终端要求,能够得到较高的制导精度。
飞行器制导控制系统正在走向智能化,“会学习”成为其显著特征[7]。而飞行器感知能力是“会学习”的重要能力支撑,实现再入参数不确定性在线辨识,对提升再入制导效果具有较大影响。不确定性参数在线辨识技术经过多年的发展,已经形成较为完备的方法体系。文献[8]研究了基于卡尔曼滤波的气动参数辨识问题,对比了扩展卡尔曼滤波算法(EKF)、无迹卡尔曼滤波(UKF)和简化UKF三种滤波估计算法,结果显示三种算法均可实现较高估计精度。文献[9]利用扩展卡尔曼滤波对飞行过程中三维风场进行辨识,实现了很高的辨识精度。文献[10]利用飞试数据对发射段风场进行辨识,辨识得到的风场与气象观测得到的风场具有良好的相似度。文献[11]在研究火星再入的过程中,利用嵌入式大气数据系统(FADS)与惯导系统耦合,成功辨识出火星再入过程中大气密度、动压、风速等参数。随着器载传感器及计算机技术发展,参数辨识辅助制导控制系统设计得到了较多关注。
但是,文献[3-6]剖面规划均更着重于剖面可行而非最优。文献[8]研究了气动参数辨识问题,文献[9-10]主要研究飞行环境参数的辨识问题,但对于大气和气动参数均存在偏差的参数辨识问题,文献[8-10]均未开展研究,文献[11]虽然能够实现对火星再入过程中大气及气动参数的联合辨识,但算法设计较为复杂,精度尚待提升。借鉴参数优化技术的设计思想,提升剖面规划最优性,并通过参数辨识,在线获取不确定性参数偏差,可改善再入制导效果,但当前,对基于气动及大气参数联合在线辨识并通过跟踪最优飞行剖面实现再入制导的研究仍较少,相关算法尚待进一步开发。
本文提出一种基于参数在线辨识的最优再入剖面规划与制导算法。首先在速度-高度剖面内设计分段解析飞行剖面,通过参数优化设计在线迭代获取飞行剖面分段点及设计参数,获得满足总吸热量最小的参考飞行剖面;其次,利用反馈线性化的方法求解制导指令并通过航迹倾角偏差进行修正,实现飞行剖面跟踪,并通过观测的过载、动压、俯仰角等参数,在线辨识飞行过程中状态及气动参数和大气环境参数,利用辨识结果修正模型及制导指令中的参数偏差,提高制导精度;最后,通过待飞航程与待飞航程预测值偏差决定是否进行剖面重新规划,并通过倾侧角符号反转实现横向制导。与前人研究相比,本文所规划的飞行剖面不但能够满足航程要求,且总吸热量最小,对飞行过程中参数偏差具有良好的辨识能力,可为升力式再入飞行器飞行轨迹设计及指标论证提供参考。
1 最优飞行剖面规划
1.1 再入运动方程
假设地球是均质圆球,三维质点再入运动无量纲方程为:
(1)
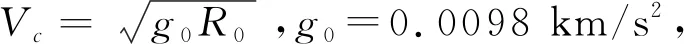
L=ρ(VcV)2SrefCL/(2mg0)
(2)
D=ρ(VcV)2SrefCD/(2mg0)
(3)
式中:ρ表示大气密度,Sref和m分别表示参考面积和飞行器质量,CL和CD分别表示升力系数和阻力系数。
1.2 再入约束
再入过程约束主要包括动压约束、热流约束、过载约束,以及平衡滑翔约束。如下所示:
(4)
(5)
n=|Lcosα+Dsinα|≤nmax
(6)
(7)
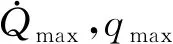
末端约束主要包含末端高度、末端速度、末端经纬度约束,表示为h(Vf)=hf,θ(Vf)=θf,φ(Vf)=φf,这里hf,θf和φf分别表示末端飞行高度、末端经度和末端纬度。
1.3 剖面拟合
在高度-速度剖面内,可以将高度拟合为速度的多项式或多项式的分段。分段拟合能够得到性质更好的飞行剖面,通过合理的段数划分,使拟合得到的飞行剖面变化平稳,设计灵活性更大。本文在高度-速度剖面内将高度拟合为两段三次多项式形式。即
(8)
式中:V0和Vf表示剖面规划的初始点及末端点,href(V)表示不同速度下参考高度待确定系数,一共有8个,且有一个分段点Vm待确定。高度对速度的导数如式(9)所示
(9)
由式(9)可见,在初始速度、高度、航迹倾角给定的条件下,初始点高度对速度导数即可确定。同样,对于末端点,高度和速度满足终端约束时,若末端航迹倾角确定,则末端高度对速度的导数也可通过上式确定。同时,为保证两段参考轨迹过渡平稳,需保证两段剖面连接点处高度相等,且高度随速度变化率相等。至此,约束条件确定了6项。而待求解参数包含8个拟合系数及一个切换点,需要进一步考虑其他约束,从而完全确定参考剖面。
1.4 剖面参数确定
通过1.3节方法,可以获得一组飞行剖面,待确定参数有3个。强约束仅剩下航程约束,为求解出所有待定参数,可选择优化某种指标函数,使之达到最优化。本文对总吸热量进行优化,总吸热量表达式为
(10)
由于本文飞行剖面设计过程中采用飞行速度作为自变量,因此将总吸热量转换成以速度为自变量的积分形式,即
(11)
使总吸热量最小,即使式(11)达到最小。在设计剖面下,有
(12)
式中:γref表示标准飞行剖面对应的航迹倾角。
再入过程中,待飞航程随速度变化的表达式为
(13)
因而航程约束可以表达为
(14)
(15)
式中:hmin(v1),hmax(v1)分别表示速度v1下速度-高度再入走廊下边界和上边界。hmin(v2),hmax(v2)分别表示速度v2下速度-高度再入走廊下边界和上边界。
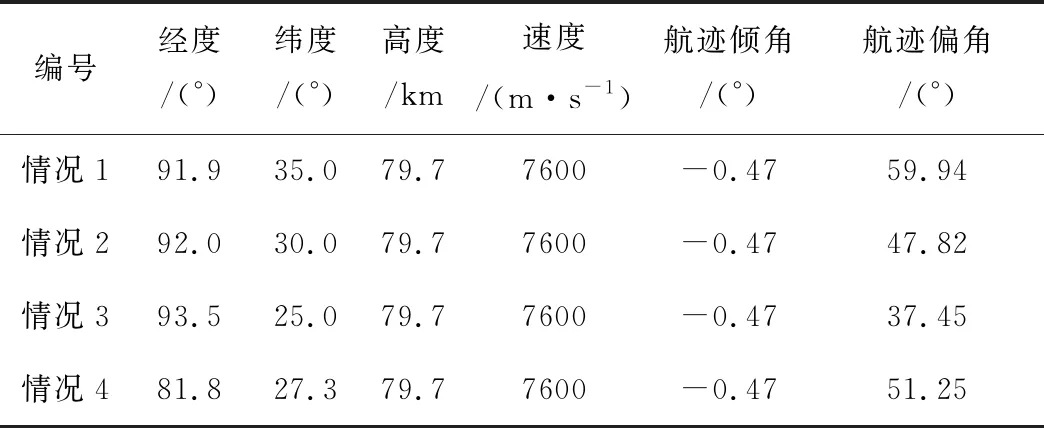
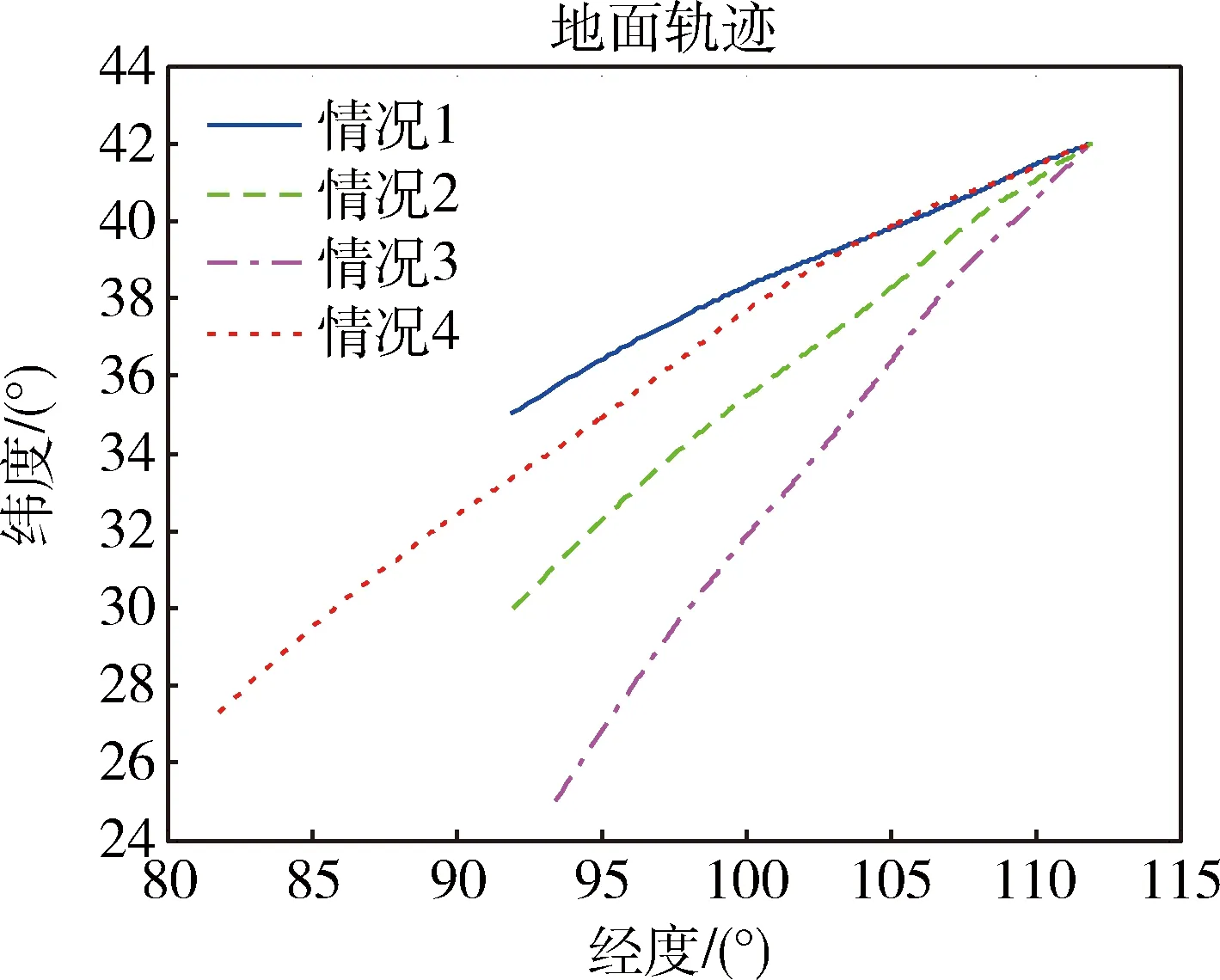
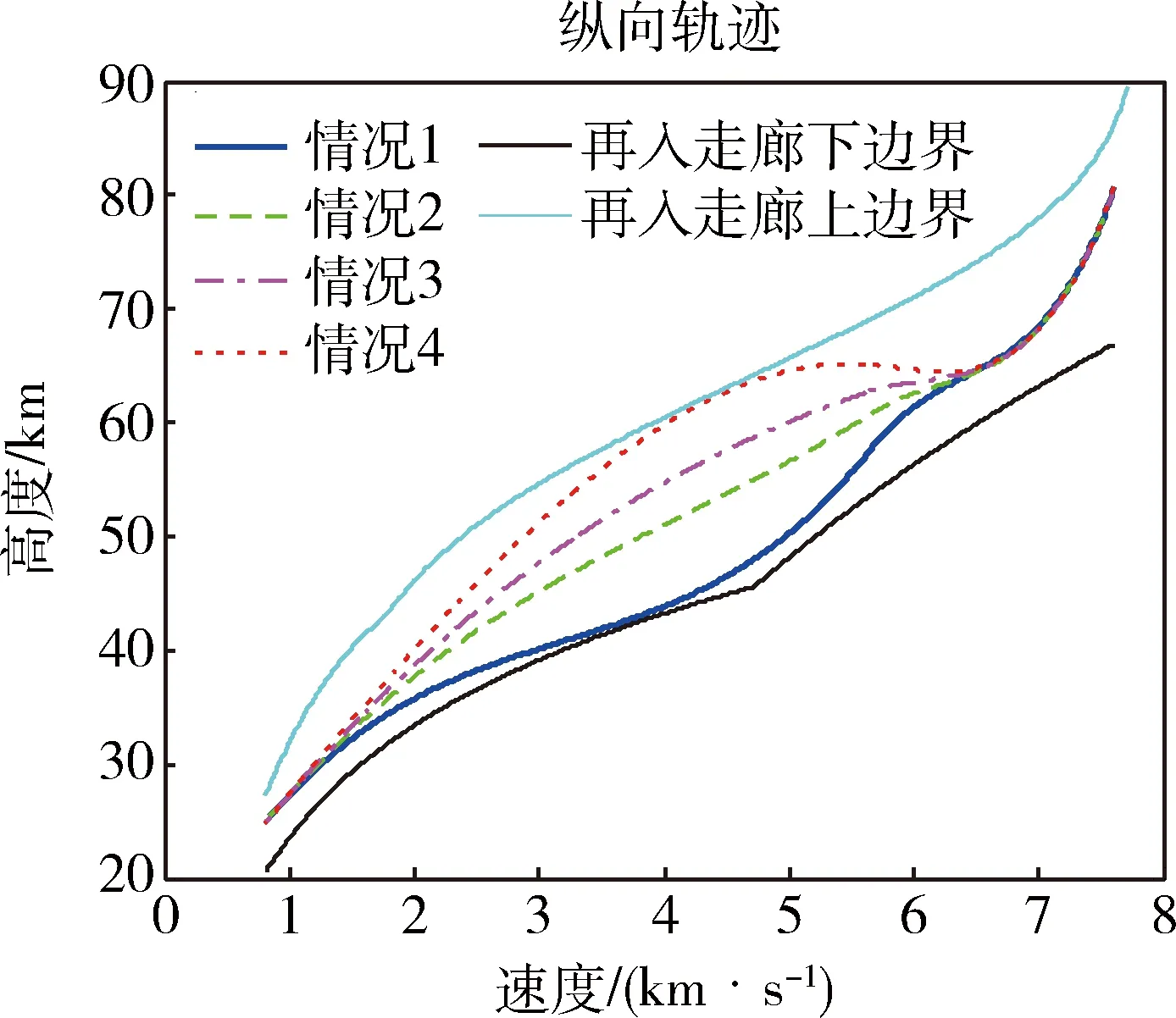
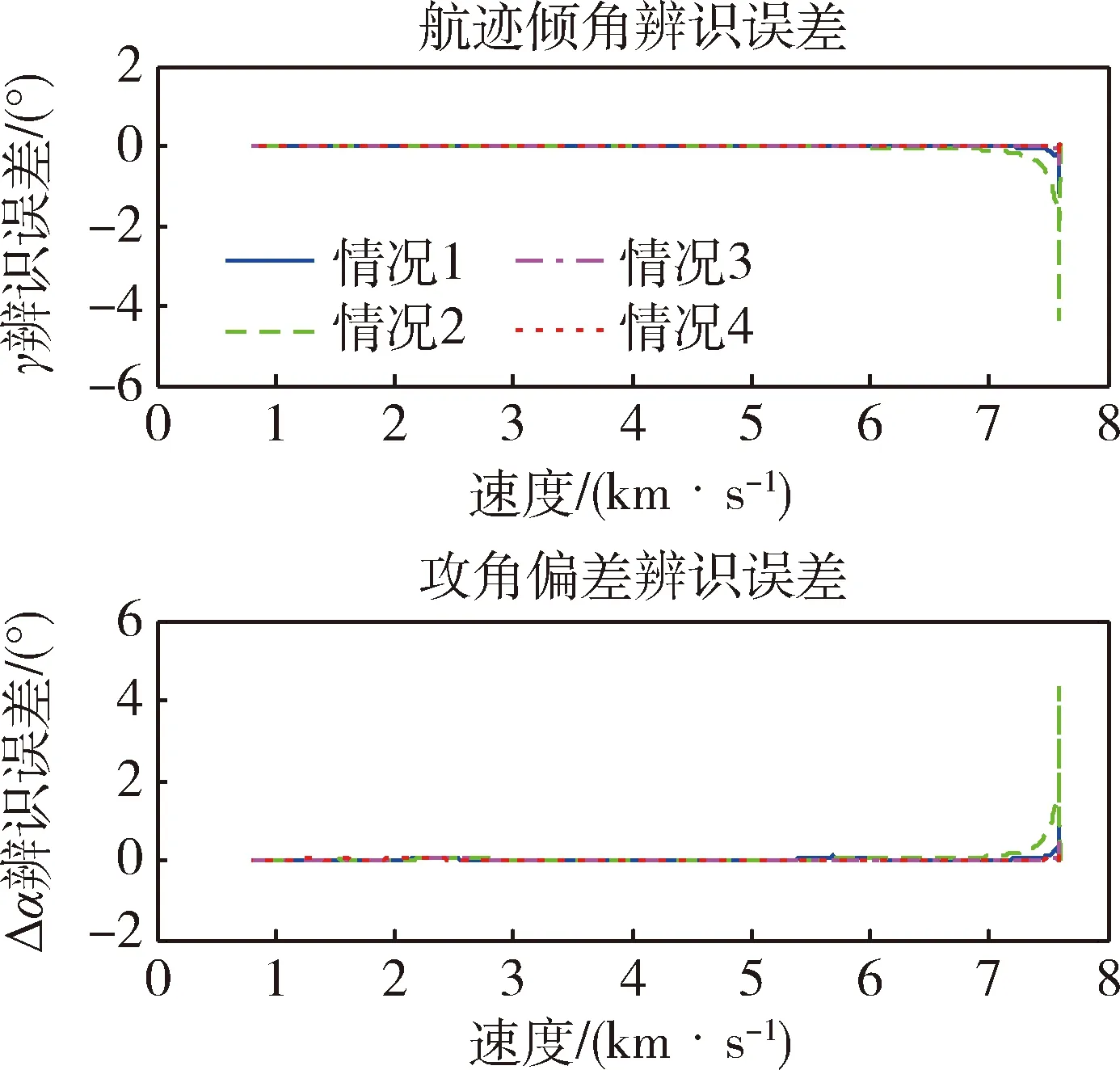
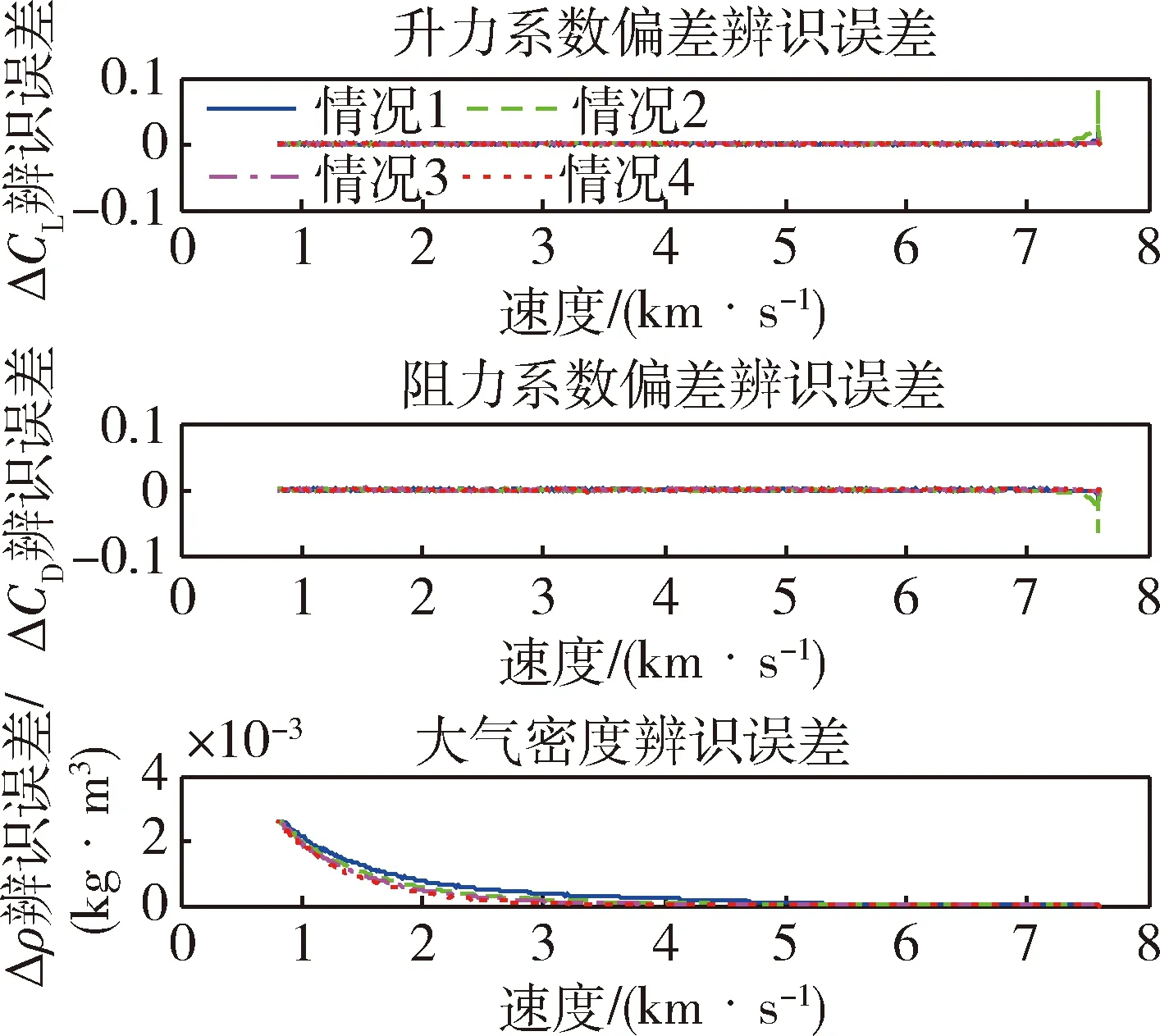
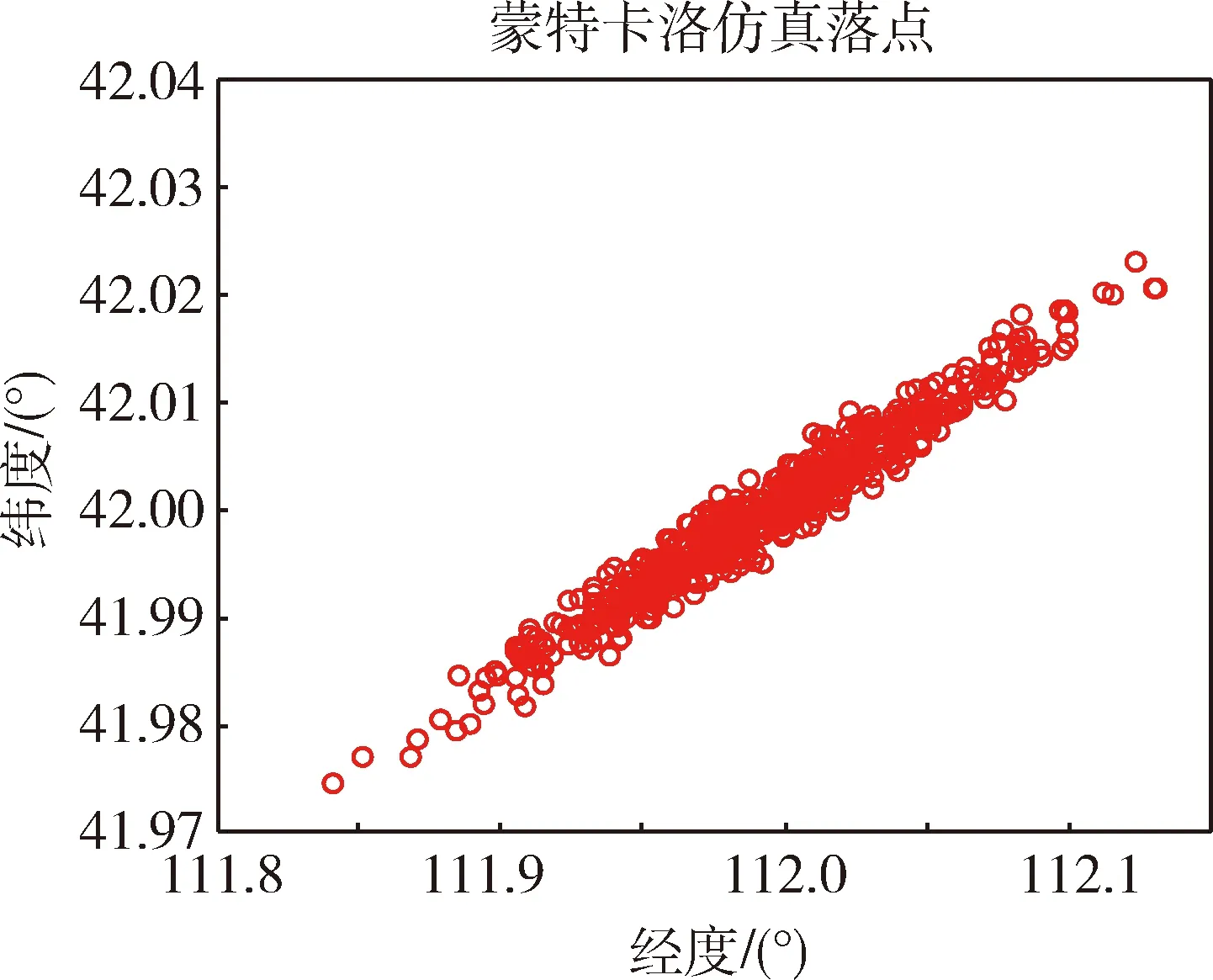
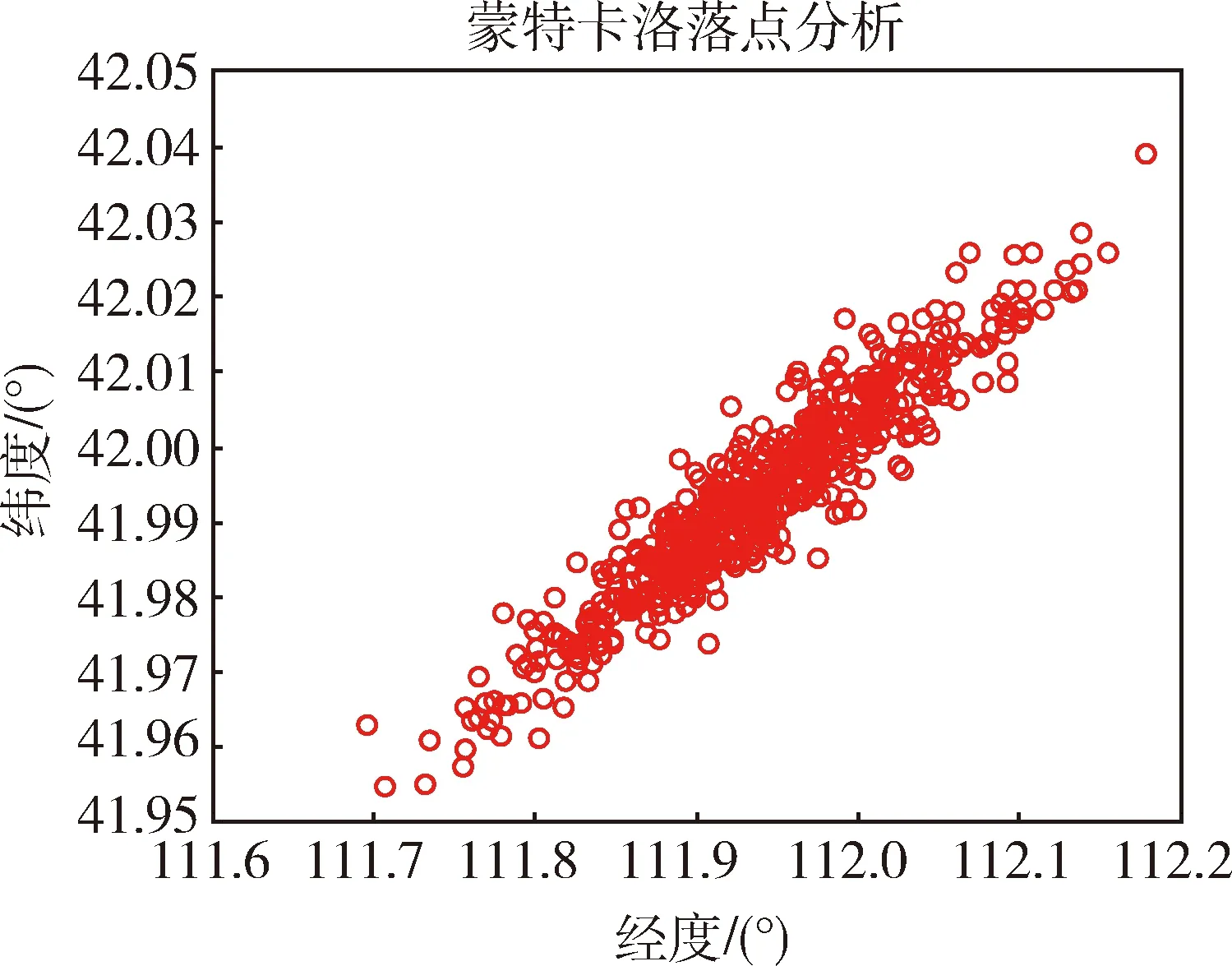
求解上述优化问题,可得两个设计点对应的高度及两个剖面的分界点速度。待求解问题中,式(11)和(15)均存在积分项,可以利用数值求积分公式转化成解析表达式形式[12]。记V0 δV=(Vf-V0)/N,Vi=Vi-1+δV (16) 记 (17) (18) 则式(15)可表达为 (19) 记 (20) (21) (22) 这里Vmin和Vmax是Vm的搜索边界。 可采用非线性数值规划算法求解上述问题,本文通过序列二次规划算法对该问题进行求解。 利用反馈线性化进行倾侧角指令求解,首先将高度对速度二次微分,可以得到 (23) 式中: (24) (25) (26) 式中:j表示第j个制导周期。标准轨迹跟踪可通过设计二阶环节跟踪器实现,即 (27) 式中:ζ和ω分别是阻尼比和自然频率。 通过式(27)形成的制导指令,可实现对标准轨迹的跟踪,但仿真发现,其收敛较慢,导致剖面更新次数增多,制导误差较大。分析式(12)可知,在标准H-V飞行剖面下,在任意速度下,航迹倾角与高度对速度变化率均是一一对应的。在式(27)形成的制导律的基础上,进一步调整倾侧角,使航迹倾角迅速收敛于标准飞行剖面对应的航迹倾角γref,即迅速实现对dhref/dV的跟踪,可改善制导的动态过程,避免跟踪过程中的振荡。使实际航迹倾角收敛于标准飞行剖面对应的航迹倾角,即实现 (28) 即 (29) 式(29)中,γ即在制导律(27)作用下产生的航迹倾角。进一步调整后的倾侧角记为σcmd。由式(29)可得 (30) 式中:Lref和Dref表示参考剖面对应的无量纲升力和阻力,K为大于0的正数,M表达为 (31) 式(30)得到的制导律可提高收敛速度,当偏差较小时,M影响较小,当实际飞行剖面收敛于标准飞行剖面时,式(30)产生的制导指令与式(27)相同。 从式(30)可见,需要反馈的参数中,升力、阻力、航迹倾角受气动参数偏差扰动及大气密度、风速扰动较大。为进一步提升制导精度,可对偏差量进行在线辨识。影响较大的待辨识参数主要包括升力系数偏差ΔCL、阻力系数偏差ΔCD、大气密度偏差Δρ和攻角偏差Δα。将偏差导数视为白噪声增广进入纵向状态方程即形成连续的状态方程,其中,ε1,…,ε6是互不相关高斯白噪声,L*,D*是受到扰动后的升力和阻力,分别计算如下 (32) (33) (34) 将(32)离散即得到滤波估计的状态方程。观测量包括高度、法向过载、轴向过载以及俯仰角,FADS等技术的发展使得动压可测。因此可得到观测方程,如式(35)所示。 (35) 系统噪声协方差矩阵记为Qk,测量噪声矩阵为Rk。至此建立了辨识扰动不确定性参数的状态方程和观测方程,它们均是非线性的,利用EKF算法进行参数辨识,由于偏差预测模型准确度较差,为得到更准确的辨识结果,本文采用渐消记忆的扩展卡尔曼滤波算法实现不确定参数的辨识[13]。至此,可得到每个制导周期内不确定性参数辨识的辨识结果,利用辨识得到的结果对运动模型、倾侧角指令及装订的攻角指令进行修正,提高制导精度。 横向制导通过改变倾侧角符号实现,表达如下 (36) 式中:航向角偏差计算如下 Δψ=ψ-ψLOS (37) ψLOS即当前位置至目标点的理想视线角,计算如下 (38) 至此,已经完成基于不确定参数在线辨识的最优再入剖面规划与制导算法设计。基本过程如图1所示。图1中,R表示待飞航程,Rpred表示待飞预测航程。 图1 算法流程 基于X-33模型进行仿真验证,该飞行器质量37363 kg,参考面积149.4 m2,仿真再入过程中,攻角(°)按马赫数装订,如下 (39) 首先对4种不同航程下的算例进行仿真验证。它们初始再入位置不同,但是交班点经纬度均为(112°,42°),交班点高度为24.87 km。升力系数、阻力系数、大气密度、攻角偏差如表2所示。 表1 初始条件 表2 参数偏差 情况1~4仿真结果如图2~4所示,图2表示经纬度变化曲线,可见均能精确到达预定目标。图3展示了高度随速度变化曲线,可直观看出,若达到较远航程,相同速度下,需要飞行高度更高。情况1由于预定航程较短,曲线已非常接近约束下边界,而情况4曲线由于航程较长,已经非常接近于平衡滑翔约束。图4是考虑了偏差及航迹倾角反馈后的制导指令。 图2 地面轨迹 图3 速度-高度曲线 图4 制导指令 图5 攻角偏差及航迹倾角辨识误差 图6 升阻力系数偏差及大气密度偏差辨识误差 图5~6表示情况1~4对表2所示偏差的辨识结果,可见对航迹倾角、攻角、升阻力系数偏差辨识结果均能快速收敛,但对大气密度偏差辨识误差逐渐增大,主要原因是大气密度偏差随飞行高度降低呈指数式增加,滤波结果呈现出滞后效应。进一步分析可发现该辨识误差占大气密度的比例呈逐渐收敛至0的趋势,因此该辨识误差对制导精度的影响逐渐降低。 为全面检验算法性能,引入初始参数偏差和状态参数偏差进行蒙特卡洛打靶仿真。蒙特卡洛打靶加入的随机偏差项如表3所示。 表3 蒙特打靶偏差项 加入不确定性辨识环节并根据式(30)产生制导指令,落点分布如图7所示,可见交班点在目标点附近,且偏差散步较小,展现出良好的适应性。若不对不确定性参数进行在线辨识,且制导指令根据式(27)产生,则偏差散布较大,且偏差较大,如图8所示。 图7 加入辨识及附加反馈后的打靶仿真交班点 图8 未加入辨识和附加反馈的打靶仿真交班点 对于最优飞行剖面规划及参数不确定条件下的制导问题,本文利用分段多项式拟合速度-高度飞行剖面,并利用序列二次规划求解得到满足总吸热量最优的拟合参数。通过反馈线性化方法并附加航迹倾角偏差反馈形成的制导指令能够保证对所设计飞行剖面的跟踪,且飞行过程中的参数偏差可以通过渐消记忆卡尔曼滤波进行准确辨识,提高了制导精确性。仿真表明本文算法适应性强,不确定性参数在线辨识并修正制导指令可有效提升制导精度。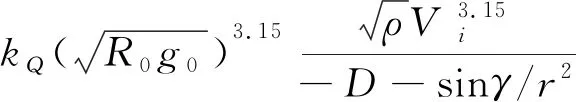
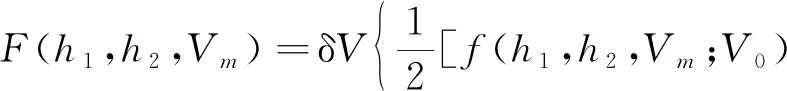

2 最优飞行剖面跟踪制导
2.1 倾侧角指令
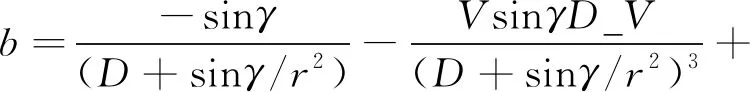
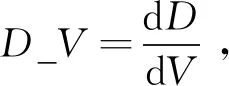
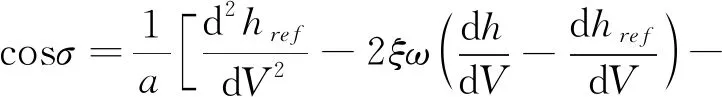
2.2 不确定性参数在线辨识
2.3 横向制导指令

3 仿真校验


4 结论
