功能梯度压电压磁圆柱轴对称的静力学响应
2021-11-17汪文帅
谢 军,李 星,汪文帅
(宁夏大学数学统计学院,银川 750021)
功能梯度材料(FGM)作为一种新型智能复合材料,最早是由日本科学家平井敏雄于1984 年提出,其特点是连续改变材料微观组成,即材料内部成分呈一定比例,宏观性能表现为连续且平稳变化,可最大限度缓和由机械作用引起的应力不均,降低结构内部应力集中、能够提高材料的断裂韧性,延长器件的寿命[1-2]。自从功能梯度材料被提出,由于其良好的性能,受到社会各界的关注。此外,压电压磁材料是智能材料系统中的一类主要材料,具有电磁弹多场耦合效应,应用前景极其广泛[3-5]。由于工程技术的需求,压电压磁器件被制成各种形状。球形、柱形压电压磁壳作为压电压磁器件的重要一类,在降低器件密度和放大其传感和制动特性方面优于其他结构的器件[6-7]。将功能梯度材料与压电压磁材料进行结合,可发挥各自的优势,极大地优化材料的性能,对新型智能材料性能的设计与利用有着重要的意义。
在功能梯度纯弹性材料的研究方面学者们进行了深入研究。Gao 等[8-9]采用了Frobenius 方法、同伦分析法求解功能梯度材料板中的声表面波问题。球形、柱形作为典型的结构,假设弹性模量按特定的函数变化,学者可用特殊函数法实现结构的力学响应分析。最常见梯度特性假设形式有幂函数形式[10-11]和指数函数形式[12],基于这样的假设,学者们通过欧拉方程、超几何函数以及级数等方法得到功能梯度材料圆柱、球壳应力分布解析解。目前单一热/电/磁场载荷下的功能梯度材料的力学相应问题已有系列研究成果。Li等[13-14]分析得到功能梯度压电柱型/球壳的静态响应的解析解;并针对任意径向非均质特性的材料,借助积分方程方法实现了电势与应力的分布数值求解。Chen 等[15]通过引入新的位移函数和应力函数,对静态压电叠层空心球的电弹性耦合问题进行研究。Yildirim[16]基于球对称假设,得到了幂函数梯度变化的球壳在稳态热载荷和内外压力载荷作用下弹性场的解析解。赵伟东等[17]应用虚功原理和变分法推导了均匀变温场中的功能梯度圆底扁球壳在均布外侧压力作用下的位移型几何非线性控制方程,运用打靶法计算获得了球壳轴对称变形的数值结果。对于功能梯度压电/压磁材料,Wang 等[18]通过引入新的因变量,采用分离变量技术,将非均匀的磁弹性空心圆柱的瞬态响应转化为Volterra 积分方程,得到了位移、应力以及磁势的完全解。Nemtollah 等[19]得到了功能梯度厚壁旋转球形压力容器在均匀的磁场内承受轴对称的机械载荷和热载荷下位移、应变和应力的解析解。此外,文献[20 - 21]假设材料特性是特殊函数,研究功能梯度压电/压磁材料中梯度系数对波的色散曲线,电磁耦合系数的影响。Shi 等[22]研究了正交异性功能梯度环形双材料结构中弧形界面裂纹的动力学行为。
以上文献研究的是单场载荷下的功能梯度材料的力学响应,对于功能梯度电磁弹材料的多物理场响应问题,时朋朋等[23]基于材料参数按幂函数梯度变化,研究多种不同场作用下功能梯度压电压磁空心球壳的耦合问题,但是多种不同场作用下功能梯度压电压磁空心圆柱的耦合问题没有研究。基于相同的幂函数梯度特性假设,本文研究弹性、电势、磁势等多种物理场载荷作用下功能梯度压电压磁空心圆柱的多场耦合静力响应,得到了功能梯度压电压磁空心圆柱内位移、应力、电势、磁势物理量的解析解。数值验证了不同边界条件作用下,功能梯度压电压磁空心柱体会产生正(逆)压电,正(逆)压磁,以及正(逆)磁电效应。同时发现,通过调整梯度参数及圆柱尺寸大小可使功能梯度压电压磁器件达到最优性能。并通过与功能梯度压电压磁空心球壳响应的比较,分析球壳与空心圆柱几何结构特点对应力、电势、磁势物理量分布的影响规律。
1 基本方程
考虑功能梯度压电压磁空心圆柱,引入柱坐标 (r,θ,z),其中z轴为空心圆柱的轴,圆柱厚度为b-a,这里a为空心圆柱的内半径,b为外半径。本文假设圆柱足够长,只考虑径向加载的情况,即位移、电势和磁势仅仅是关于r的函数。这种情况下,功能梯度压电压磁空心圆柱本构方程为[24]:
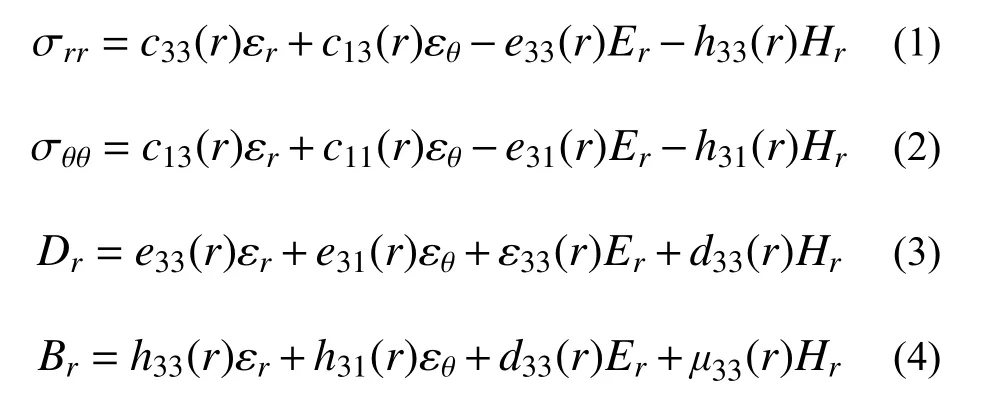
式中: σrr(εr)、σθθ(εθ)分别为空心圆柱径向应力(应变)、环向应力(应变)分量;Dr为电位移分量;Er、Hr、Br分别代表电场、磁场以及磁感应强度;cij、ei j、ε33、hij、d33、μ33依次为弹性、压电、介电、压磁、磁电耦合和磁导率系数。本文假设这些材料参数以幂函数梯度变化[25]:

2 边界条件
对于压电压磁材料而言,一般有多种边界条件,最常见的有力载荷边界条件、电场边界条件和磁场边界条件以及含以上两(三)种物理场的混合边界条件。本文考虑了三种边界条件,分别如下:空心圆柱内表面承受压力作用 (Case A),空心圆柱内外表面存在电势差 (Case B),以及空心圆柱内外表面存在磁势差 (Case C)。对应边界条件表示为:


这里Case A 对应传感器模型,即对压电压磁材料来说,施加载荷产生电场和磁场,Case B 和Case C 分别对应电场和磁场作动器模型,即电势差作用产生应力和磁场,以及磁势差作用产生应力和电场。
3 问题通解



4 数值算例分析
首先,这里对本文得到的解析解进行验证。令式(1)~式(4)中h33=h31=d33=0,并采用与文献[13]相同的其他材料和结构参数,则本文的解析解退化为文献[13]中给出的功能梯度压电空心圆柱的解析解。
图1 与图2 给出本文解析解的退化结果与前人的解析解的对比。可以看出,两种解析解得到的圆柱应力、电势的结果完全一致,即基于本文解析解的退化解与前人解[13]完全吻合。
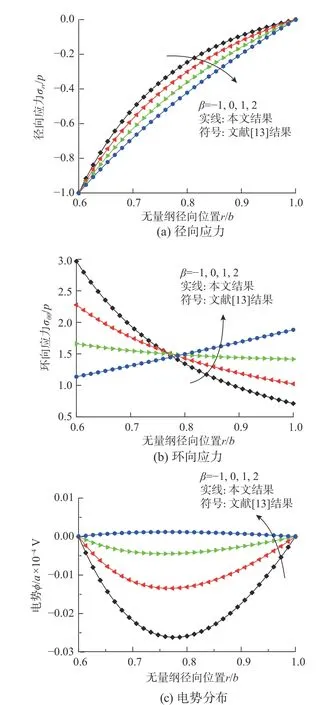
图1 功能梯度压电空心圆柱沿厚度方向的应力、电势分布:p=c33×10-4 MPa, a/b=0.6Fig. 1 Stress and electric distributions along thickness direction of FGPE hollow cylinder: p= c33×10-4 MPa, a/b=0.6

图2 功能梯度压电空心圆柱沿厚度方向的应力、电势分布:V=(106×a)V, a/b=0.6Fig. 2 Stress and electric distributions along thickness direction of FGPE hollow cylinder:V =(106× a )V, a/b=0.6
下面,选择常见的复合材料BaTiO3-CoFeO4进行数值分析,材料参数见表1。

表1 BaTiO3-CoFeO4 材料参数Table 1 Material parameters of BaTiO3-CoFeO4
对于空心圆柱,其应力、电势和磁势的数值模拟结果如下所述。
图3 给出功能梯度压电压磁空心圆柱传感器内部受压(Case A)作用下,应力、电势以及磁势沿径向分布。由图3(a)及图3(b)看出,径向应力受梯度参数 β的变化影响较小,而环向应力受影响要大的多,所以环向应力过大会引起此类传感器的破坏。图3(a)可看出,当参数 β增大时,径向应力也逐渐增大。图3(b)发现 β对环向应力变化趋势影响很大,无论梯度参数 β的正负,环向应力绝对值都随厚度r增大而递减,且环向应力随着 β增大而逐渐平缓。这也说明,在设计此类传感器过程中,注意选择恰当的梯度参数不仅有效降低结构内部的环向应力,也可以让变化趋势趋于平缓,从而避免因过高环向应力而产生结构破坏。图3(c)和图3(d)给出了 β ∈[-0.5,1]下压电压磁空心圆柱传感器的电势、磁势分布。当空心圆柱传感器受到载荷时,内部产生应变,在内外表面上产生符号相反的电荷,进而引起内部电势变化;同时也引起内部磁势和磁场的变化,这称为压电效应与压磁效应。传感器受力变形所产生的电势差与所受载荷大小成正比。相对非功能梯度压电压磁( β =0的情况)材料,梯度参数大于零相当于整体弹性系数增大,这样相同载荷下的形变减小,因此 β逐渐增大时,电势会减小。从图中发现,在r/b=0.7附近,电势以及磁势绝对值均达到极大值,这也经常导致结构的破坏。这些响应结果由纯载荷作用产生。同时看出梯度参数对磁响应影响很大,这意味着磁势曲线对 β很敏感。简要总结,这些结果表明,适当调整梯度系数,可以获得所需的电磁力耦合性能。
图4 给出作为作动器的空心圆柱内部受到电激励时(Case B 内外部存在电势差),空心圆柱各个物理量沿径向的变化情形。将电信号输入压电压磁圆柱作动器,从图4(a)、图4(b)以及图4(d)发现,圆柱内部存在非零的力学响应和磁势响应,即逆压电效应、正磁电效应。从图4(a)、图4(b)中发现,与Case A 不同,当此类作动器输入电信号时,结构内部产生的环向应力要比径向应力敏感的多,且随 β的增大,环向应力绝对值也增大,这是引起器件破坏的重要因素。图4(c)可以看出,空心圆柱内部电势随 β增大而减小。图4(d)在无量纲位置r/b=0.7附近,磁势绝对值均达到最大值。类似于图3,从图4 中同样发现通过调节 β有效的防止因环向应力过大引起柱体破坏,提高器件寿命。

图3 功能梯度压电压磁空心圆柱体传感器内受机械载荷下磁电弹响应的径向分布(Case A):p=1×106 MPa, a/b=0.5Fig. 3 Radial distribution of magneto-electro-elastic sensor under mechanical load inside FGPEPM hollow cylinder(Case A): p=1×106 MPa, a/b=0.5
图5 给出作为作动器的空心圆柱内部受到磁励时(Case C 内外部存在磁势差),空心圆柱的各个物理量沿径向的分布规律。类似于图4,当存在磁信号时,由图5(a)、图5(b)以及图5(c)发现,作动器内部产生非零力学响应及电势响应,称之为逆压磁效应和逆磁电效应。从图5(a)看出,在无量纲位置 0.65 <r/b<0.7附近,径向应力达到最大。由图5(c)看出,结构内部电势绝对值随 β的增大而先增大,在无量纲位置r/b=0.7处,电势有最大值,后随之减小,从图5(d)可知磁势随 β的增大而减小。当圆柱输入电或相关磁载荷时,由式(1)~式(4)知电磁参数在问题求解过程中的地位是对立的,因此,图4(a)~图4(d)中的结果在形态上分别与图5(a)~图5(d)几乎一致。图5 结果同样表明 β对此类复合材料的多场耦合性能产生巨大影响。

图4 内外表面电势差下功能梯度压电压磁空心圆柱体的磁电弹力响应分布(Case B):V=100 V, a/b=0.5Fig. 4 Distribution of magneto-electro-elastic response value of FGPEPM hollow cylinder under potential difference between inner and outer surfaces (Case B): V=100 V, a/b=0.5

图5 内外表面磁势差下功能梯度压电压磁空心圆柱体的磁电弹力响应分布(Case C):Q=100 A, a/b=0.5Fig. 5 Distribution of magneto-electro-elastic response value of FGPEPM hollow cylinder under magnetic potential difference between inner and outer surfaces(Case C): Q=100 A, a/b=0.5
图6~图8 给出空心圆柱传感器内部受机械载荷、电激励、磁激励时不同空心圆柱尺寸(即厚度)对逆压电、逆压磁、逆压磁以及逆压电效应响应的影响。这里梯度参数β 分别取-1 和1,比较图6发现,在不同尺寸下电势与磁势都有峰值,从图7发现,当 β取-1 与1 时,电势与磁势的变化趋势相同,且不同尺寸下应力与磁势都有峰值。同时发现,随着无量纲尺寸的增大,其峰值向右平移且峰值的大小都逐渐减小。比较图8(a)与图8(c)、图8(b)与图8(d)发现,梯度参数 β值的正负不影响径向应力与电势变化趋势,只影响其取值的大小,且对其值的影响较大。从图6~图8 看到,不同边界条件下,不同厚度对功能梯度空心圆柱的力场、电场以及磁场有较为明显的影响,这也表明给定梯度参数时,调整圆柱尺寸可得到最优的电磁力耦合性能。

图6 空心圆柱尺寸对压电和压磁效应响应的影响(Case A):p=1×107 MPaFig. 6 Influence of hollow cylinder size on response of piezoelectric and piezomagnetic effects (Case A): p=1×107 MPa

图7 空心圆柱尺寸对应力和磁电效应的影响(Case B):V=100 VFig. 7 Influence of hollow cylinder size on stress effect and magnetoelectric effect (Case B): V=100 V
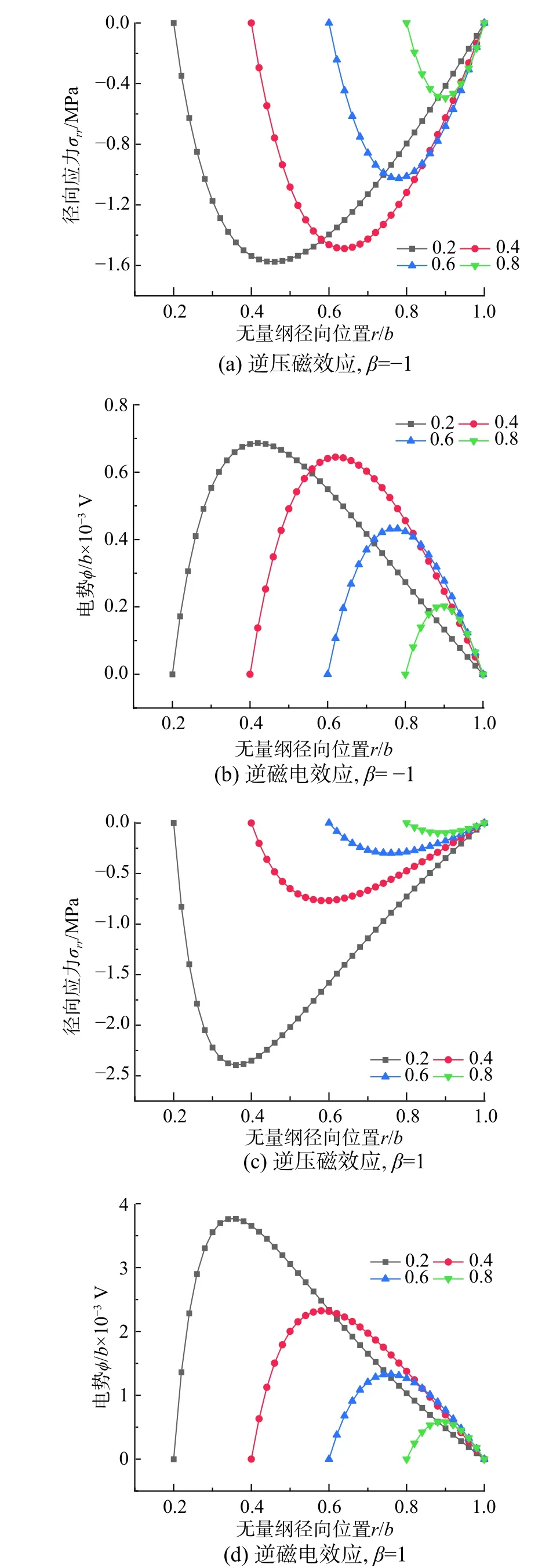
图8 空心圆柱尺寸对应力和逆磁电效应的影响(Case C):Q=100 AFig. 8 Influence of hollow cylinder size on stress effect and piezoelectricity effect (Case C): Q=100 A
下面给出文献[23]情况A 中压电压磁空心球壳的应力、电势与磁势分布图,并与图3 压电压磁空心圆柱的应力、电势与磁势分布进行对比。比较图3 和图9,可以发现,当对压电压磁材料施加机械载荷时,对于径向应力的大小和变化规律而言,空心圆柱与球壳保持基本一致。图3(b)和图9(b)表明,空心圆柱的环向应力的绝对值几乎是球形壳的两倍。此外,随着梯度参数 β增加,空心圆柱/球壳的环向应力沿厚度趋于均匀。从图3(c)和图9(c)可以看出,在相同的梯度参数 β参数下,空心圆柱的电势绝对值大于球壳中的绝对值,其极值出现在r/b=0.65 附近;随着梯度参数 β增加,电势绝对值的最大值将减小。从图3(d)和图9(d)可以看出,在磁势分布中,梯度参数对压电压磁空心圆柱磁势分布有很大影响,对球壳磁势分布的影响较小。

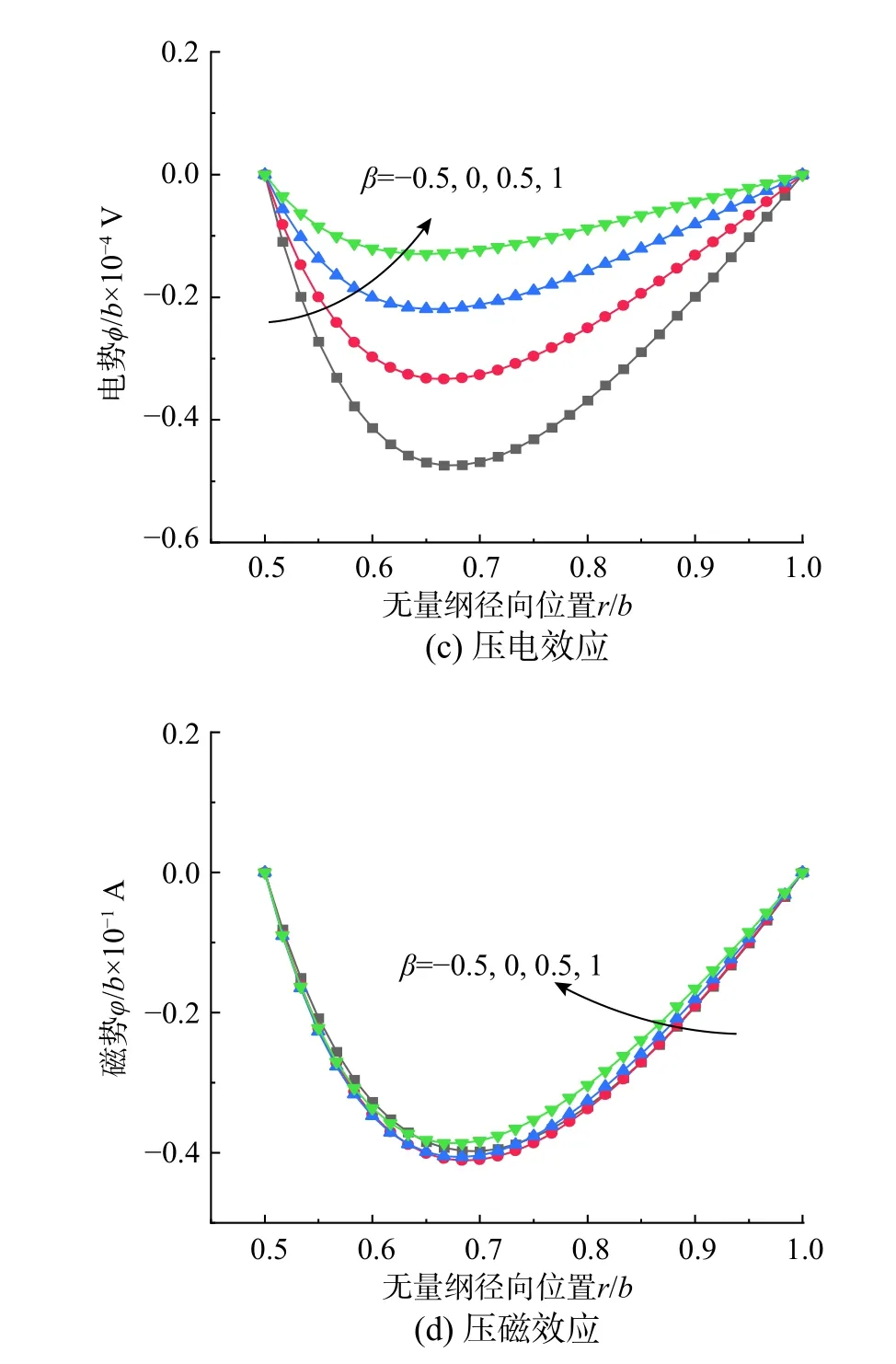
图9 功能梯度压电压磁空心球壳传感器内受纯机械载荷下磁电弹响应的径向分布(Case A):p=1×107 MPa, a/b=0.5Fig. 9 Radial distribution of magneto-electro-elastic sensor under pure mechanical load inside FGPEPM spherical shell(Case A): p=1×107 MPa, a/b=0.5
5 结论
基于经典弹性理论,本文假设功能梯度空心圆柱的物理参数沿径向呈幂函数变化,研究了功能梯度压电压磁空心柱体在三种边界条件作用下结构内部电磁力多场耦合响应,得到应力、电势和磁势等物理量的解析解,最后分析了梯度参数和空心圆柱厚度对应力、电势和磁势分布的影响。文章的结果可以退化到均匀压电压磁空心柱体的解析解以及弹性材料空心圆柱的解析解。通过数值算例,对BaTiO3-CoFeO4复合材料进行了数值计算与模拟,图解得到了应力分量、电响应、磁响应的分布。从数值结果中发现,为了能更好地避免由应力过大而引起的柱体的开裂,提高压电压磁器件的准确性和使用寿命,建议通过调整梯度参数,这样可降低环向应力分布,使之趋于稳定,同时发现当功能梯度空心圆柱梯度参数给定时,通过调节尺寸可减小应力的峰值,也起到相同作用。总而言之,对于功能梯度压电压磁空心圆柱,选择不同的梯度参数以及不同尺寸大小都会大大影响压电压磁空心柱体的电磁力耦合性能,因此调整梯度参数与尺寸可使功能梯度压电压磁器件达到最优的磁电弹多场耦合性能,同时提高材料的力学性能。
附录:

