不同海况下立管参数对中国灯笼型CALM系统的影响研究
2021-11-17张大朋赵博文王少鹏
张大朋,严 谨,赵博文,王少鹏,李 俊
1.广东海洋大学海洋工程学院,广东湛江 524088
2.浙江大学海洋学院,浙江舟山 316021
3.杭州艾美依航空制造装备有限公司,浙江杭州 324100
4.宁波欧佩亚海洋工程装备有限公司,浙江宁波 315000
虽然单点系泊系统的研究成果较多,针对中国灯笼型CALM系统的研究却寥寥无几[1-6],由于呈中国灯笼形状分布的水下立管的扭矩在不同海况下对CALM系统整体的影响有所不同,并且考虑到管内流效应的存在,对CALM系统动力响应的影响会变得更加复杂,因此本文将重点探究水下立管存在管内流的情况下中国灯笼型CALM系统的动态响应。
1 计算理论
1.1 管内流效应
大部分情形下,管道的管内流效应是可以忽略不计的。然而对于密度较高且流速较快的管内液体,其对管道力学特性产生的影响是不可忽视的。除重力之外,管内流同时还会带来三个附加力,即离心力、由于管内流流速与立管截面转动角速度相互耦合而产生的科氏力以及由于液体的黏性而导致的液体摩擦力[7]。可以通过穿过管道某一节点的流体来计算该处的离心力。流体穿过某节点时瞬时方向的单位矢量记为μi,穿出时记作μo,对于管道分段之间的节点来说,μi代表节点前分段的方向,μo代表节点后分段的方向,但值得注意的是,对于末端不受任何约束的缆绳两端的节点来说,μi、μo所代表的意义是相同的[8-10]。
因此流入、流出某一节点的瞬时速度矢量可分别表示为 Viμi、Voμo,Vi和 Vo分别为数值大小,因此流入部分的动量对于时间的导数为同样流出部分的动量对于时间的导数为从而可得作用在该点的离心力为[11-13]:

式中:Fc1为作用在凝集质量点上的离心力,kN;ρ为立管内液体密度,t/m3;Vi、Vo为流入、流出管道某节点流体速度的大小,m/s;So、Si分别为出入口截面面积,m2。
由于管道各个分段的运动导致了其内部液体科氏力的产生,因此对于任意两个相邻的节点Nj、Nj+1之间的管道分段来说,可以利用全局坐标系G-xyz和固结在Nj点上局部坐标系L-xyz来描述其内部液体的运动,向量μ的方向与Nj指向Nj+1的方向一致。
从液体相对局部坐标系的流动速度νL可得出全局坐标系下的流动速度νG的表达式:
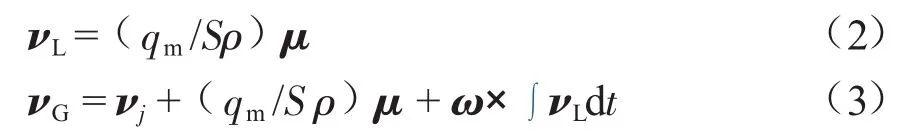
式中:νL、νG的速度单位均为m/s;μ表示单位速度向量方向;S为立管的内部横截面积,m2。
因此在全局坐标系下管道某一节点的加速度可表示为:
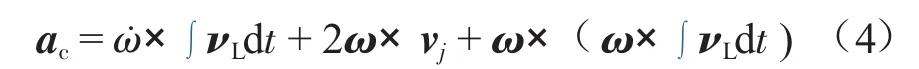
式中:ω为移动坐标系相对于固定坐标系的转动角速度,rad/s;ac为节点加速度,m2/s。
该表达式中第二部分为科氏力所引起的加速度分量,因此科氏力的表达式为:

式中:l为分段长度,m;qm为单位长度的管内流液体质量,t/m;O表示向量vj+1-vj与单位向量μ之间的夹角,(°)。
1.2 海洋管道与CALM浮标的水动力特性计算原理
在对海洋管道进行计算分析时,假定其为挠性结构。采用凝集质量法对海洋管道进行建模,考虑重力、浮力、张力等,将管道离散为凝集质量模型,由若干个连续的、无质量分段和处于各分段中点处的节点组成。每个分段是一个连续的、无质量的缆索元,只考虑其轴向和扭转特性,将其模拟为轴向、旋转弹簧和阻尼器的组合体。而节点集中了两个相邻分段各一半的质量,力和力矩都作用于节点上。关于凝集质量法的详细推导情况,笔者在文献[14-16]及个人专著[17]进行了详细的推导,这里不再展开。CALM浮标在OrcaFlex中可以被看做是6自由度的Spar浮标,通过将相关的水动力特性参数及几何尺寸赋予Spar浮标后即可对CALM浮标的水动力特性进行计算。立管及CALM浮标的具体参数取自文献[18]。
2 数值模型
中国灯笼型立管CALM系统模型如图1所示,模型中的CALM浮标所处海域水深为28 m,系统由一个CALM浮标以及系固在浮筒上的锚链、立管、系船缆及漂浮软管组成,其中两根立管的轮廓沿自身缆长呈中国灯笼形状分布。浮筒高6.166 m,重1 970.0 kN,重心位于距底部5.5 m处,系泊系统由呈向外散射的6根锚链组成,原油经过CALM浮筒输送至水下立管底部,水下软管从CALM浮标底端延伸至海床处,软管两端分别安装有隔离阀加固结构[18]。
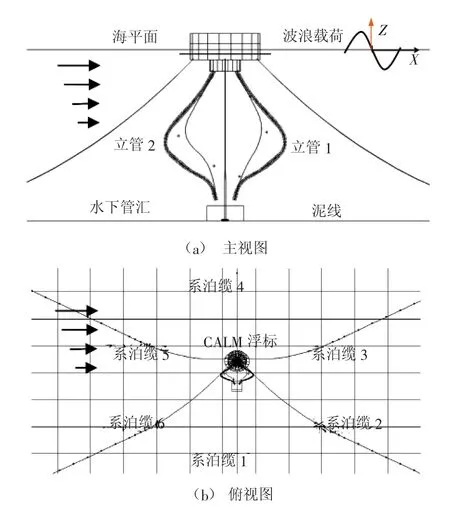
图1 中国灯笼型立管CALM系统模型示意
3 算例分析
文中在探究CALM系泊系统的动态响应时,海况是主要的环境变量。根据文献[19-20]中对海况的描述,载荷方向为350°,选取其中三种海况考察水下立管的扭矩对系泊系统整体的影响,海况参数见表1。

表1 海况参数
3.1 水下立管的扭矩对系统整体的影响
不同海况下CALM浮标的运动谱密度如图2所示。
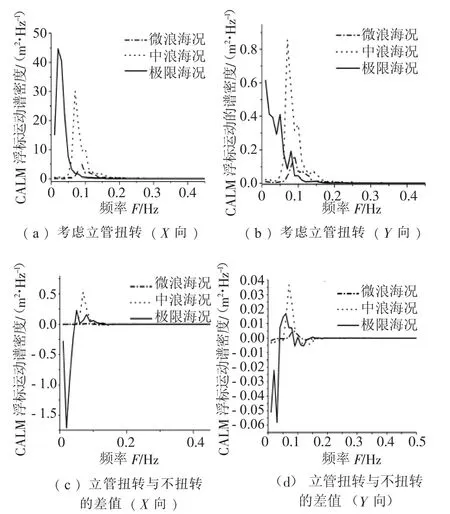
图2 不同海况下CALM浮标的运动谱密度
图2(a)、(b) 两图表示考虑了水下立管扭转作用时,CALM浮标在X、Y方向的运动谱密度分布情况。对比图2(a)、(b) 可知,由于环境外载荷方向均为350°,因此CALM浮标在X方向的运动谱密度值较大,在(a)图中,随着海况的不断恶劣,相应谱密度峰值在不断地增加,与此同时与该峰值相对应的频率却在不断减小,CALM浮标在该方向的运动回复周期增长;值得注意的是,在(b)图中,CALM浮标在极端海况下沿Y方向的运动谱密度要小于中等海况下的相应谱密度,这说明了该海况下的浮标在各自由度的运动方面具有比其他海况更强的耦合程度。
图2(c)表示CALM浮标在X方向考虑水下立管的扭转作用时谱密度减去不考虑该作用时谱密度的差值;而图2(d)为相同海况下Y方向的谱密度的差值。观察图2(c)、(d) 两图可知,在极端海况下,立管扭转作用的存在一定程度地减少了CALM浮标运动谱密度,但同样可以看到,中等海况下扭矩的存在增加了CALM浮标的运动谱密度,这说明在不同海况下,立管扭转作用的存在对于CALM浮标运动的影响是不断变化的,后续讨论中为使得计算结果更加精确,所有算例中的水下立管均处在中浪海况且考虑其自身扭矩条件。
图3为中浪海况下考虑扭转与不考虑扭转时两根立管曲率的差值沿长度方向的变化。

图3 中浪海况下考虑扭转与不考虑扭转时两根立管曲率差值沿长度方向的变化
观察图3可知,对于背浪侧的立管1而言,扭矩对其曲率的影响基本上可以忽略,但对于迎浪侧的立管2来说,扭矩的存在能够有效地减少立管在X、Y方向沿立管长度方向分布的曲率。这表明,扭矩使得立管2尽量稳定在了其处于静平衡位置时的垂直面内;观察立管1与立管2的曲率差值,可以明显地发现,在X、Y方向上,扭矩加强了两立管在空间形态上的对称性,值得注意的是,在Y方向,扭矩对两立管对称性的加强作用要明显高于X方向。这对减少立管的不必要损坏以及增加CALM系统的整体稳定性具有重要意义。
3.2 管内流对中国灯笼型立管系统动力响应的影响
图4为管内流流速的对称性对CALM浮标运动谱密度的影响。图4中(3 m/s,3 m/s) 表示立管1和立管2的管内流流速是对称分布的,其值均为3 m/s;(0 m/s,3 m/s) 表示立管1和立管2的管内流流速是非对称分布的,其值分别为0m/s、3m/s。CALM浮标的运动谱密度曲线显示,由于风浪流等外载荷以X方向为主,因此浮标的运动也以该方向为主,因此对比(a)、(b)两图可以发现:X方向运动谱密度峰值远高于Y方向。在该曲线图中,非对称管内流对CALM浮标在X、Y方向的运动产生的影响基本一致。非对称的管内流加剧了浮标原有的谱密度峰值,但是对于其峰值所对应频率的影响很小,在两根立管的管内流流速分布对称均为3 m/s时,其浮标的运动谱密度值要小于非对称管内流流速条件下的管内流。以上结果说明,在相同时间内,运输同样质量的原油或其他液体的情况下,两根立管的管内流流速对称能够降低CALM浮标的运动谱密度,对于降低CALM浮标的运动剧烈程度有一定的积极意义。
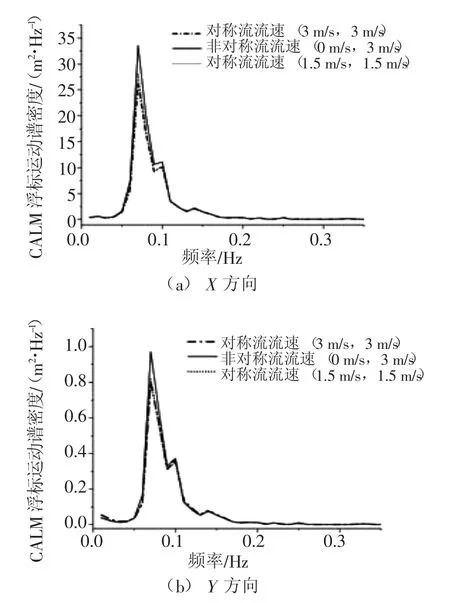
图4 管内流流速的对称性对CALM浮标运动谱密度的影响
图5为管内流流速的对称性对立管张力谱密度的影响。对比立管不同管内流流速下立管的有效张力谱密度曲线可以发现,在立管1和立管2靠近浮筒端的有效张力谱密度曲线中,管内流流速非对称时立管靠近浮筒端有效张力谱密度峰值并未随其管内流流速的降低而有所减小,而是在0.24 Hz时其张力谱密度峰值要高于对称管内流时的立管张力谱密度,且在立管2末端有效张力谱密度曲线中,非对称管内流作用下在各频率处的立管张力谱密度均大于同等海况下的对称管内流流速时的立管张力谱密度。这种现象表明,管内流的不对称分布,不仅会对立管2的靠近浮筒端张力产生影响,而且还会加剧立管1近浮筒端的有效张力。进一步对比图5(c)、(d)两图可知,对于非对称管内流(0m/s,3m/s)及对称管内流(3 m/s,3 m/s) 时的计算结果来说,迎浪侧的立管2的末端张力谱密度要远高于背浪侧的立管1末端的张力谱密度。
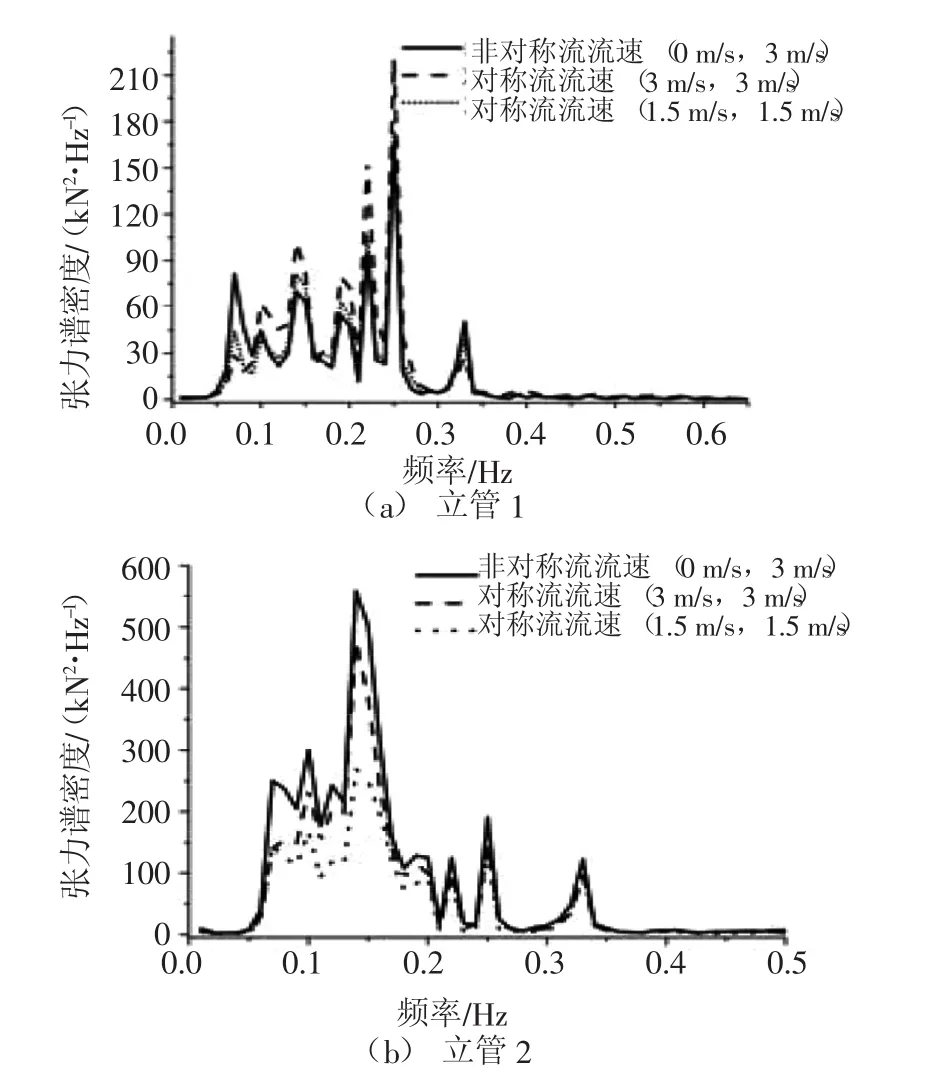
图5 管内流流速的对称性对立管张力谱密度的影响
值得注意的是,为实现在相同时间内输送同等质量的管内液体的目的,不管从CALM浮标的运动约束方面,还是近浮筒端立管末端有效张力方面来说,采用对称管内流流速(3 m/s,3 m/s)的方式输送液体都要优于非对称的输送方式。
图6为对称管内流流速对CALM浮标运动谱密度的影响。结合前面的计算结果可知,在中国灯笼型CALM立管系统中立管的管内流采用对称流动具有一定的优势,其力学特性和动力学特性方面的优点都十分显著。因此以下部分将围绕管内流为对称性流动时进行相关探讨。根据工程实际情况,管内液体为重油,取其密度为1.2 t/m3,管内流流速控制在0~3 m/s范围内。

图6 对称管内流流速对CALM浮标运动谱密度的影响
观察图6可知,随着管内流流速的增加,立管对CALM浮标在X、Y方向上运动约束也在逐步加强,图4中所示的对称流动的两个示例即可很好地说明这点,由于随着立管内液体流速的增加,液体所产生离心力的增加,立管两端的有效张力也随之增加,在这种情况下,虽然CALM浮标的运动能够得到有效约束,但这都是以增大立管的末端张力为前提的,这说明管内流流速越大,对立管近浮筒端的接头结构造成破坏的可能性越强。
图7(a)表示当管内流为对称管内流时,随着管内流流速的变化立管1和立管2近浮筒端有效张力的极值分布情况。观察图7(a)可知,随着管内流流速的增大,两根立管末端张力也随之增加,但是立管2的增长趋势要明显大于立管1,结合图7中的CALM浮筒运动谱密度逐渐降低这一事实,迎浪侧的立管2在CALM浮标运动的约束方面起到了主要作用。图7(b)、(c) 表示随着管内流流速的增加,立管在X、Y方向上的运动投影极值分布情况。对比图7(b)、(c) 两图可知,在X方向上,管内流流速的增加对该极值几乎没有影响;与X方向的结果相反的是,在Y方向,随着管内流流速的增加,立管2逐渐向Y轴负方向运动,这加剧了CALM浮标系泊系统整体的不对称性,这也是图7(a) 中立管2末端有效张力最大谱密度增加趋势比立管1大很多的主要原因。因此,综合图7可知,随着管内流流速的增加,会导致迎浪侧的立管2在环境外载荷方向的法向产生更大的运动分量,这种运动分量的产生会对立管近浮筒端接头的结构强度产生一定的破坏。
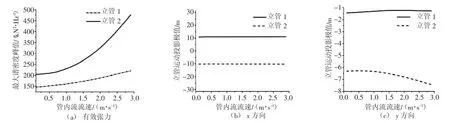
图7 对称管内流流速对立管动力学特性的影响
4 结论
采用凝集质量法计算了简化模型中系泊缆以及立管的有效张力,利用Stiffener Attachment模块等效替代立管末端的加固构件。在JONSWAP谱波浪的作用下,探究了水下立管的扭矩、立管管内流的非对称流动及对称流动时液体的流速对CALM系统的影响,结论如下:
扭矩对CALM浮标运动谱密度的影响是随着海况不断变化的,在工程实际中应根据当地海况条件找到适用于该系统的立管最佳扭矩;扭矩对背浪侧的立管1的曲率及运动极值的影响基本可以忽略,对于迎浪侧的立管2来说其曲率及沿X、Y方向的运动极值受到了很好的约束,尤其在靠近立管中点分段处约束效果最明显。
不管从CALM浮标的运动约束方面,还是近浮筒端立管末端有效张力方面来说,相同时间内输送同等质量的管内液体,采用对称输送的方式都要优于非对称的输送方式。
当管内流分布为对称管内流时,随着管内流流速的增加,CALM浮标的运动谱密度能得到一定程度的约束,但这是以增加水下立管(以立管2为主) 的末端张力为前提的,这不利于立管与CALM浮标接头处的结构稳定;对于背浪侧的立管1而言,管内流流速的增加对其各方向的运动极值几乎没有影响,随着管内流流速的增加,迎浪侧的立管2会在环境外载荷方向的法向产生运动分量,这种运动分量的产生显然会对立管近浮筒端接头的结构强度产生一定的破坏。
