“穿越沙漠”中的最大资金剩余量问题探究

余 馨，陈 云，俞旭燕

（徐州工程学院 a. 金融学院； b. 信息工程学院， 江苏 徐州 221018）

现有一种“穿越沙漠”游戏：玩家可根据一张地图，在沙漠中从起点出发行走至终点，沙漠中有晴朗、高温、沙暴三种天气情况，玩家可利用初始资金购买一定数量的水和食物，也可在矿山、村庄补充资金或资源，最后在规定的时间内到达沙漠终点，并尽可能保留更多的资金。整个游戏共六个关卡，每个关卡的参数设定、天气状况、路线地图都不相同[1]。本文拟对2020 年全国大学生数学建模大赛B 题“穿越沙漠”中的最大资金剩余量问题进行研究。

1 解决问题一的动态规划算法

赛题一包括第一关和第二关，在规定的时段内每天天气状况事先全部已知。

1.1 动态规划与状态转移

动态规划的前提是状态转移。在沙漠行走，离不开水和食物资源。玩家在每天的资源保有量基础上做决策，将决定下一天的资源剩余量，形成状态转移。

玩家选择停留、行走或挖矿，对资源的消耗量分别是基础量的 1、2、3 倍，故设 i=1，2，3，xki∈（1，0）表示第 k 天对 i 的选择与否。

记αj、βj（j=1，2，3）为晴朗、高温、沙暴天气对水和食物的基础消耗量，ykj∈（1，0）表示第 k 天是否为第j 种天气，这均为已知参数[1]。

又设A、B 为在起点购买水和食物的数量，ak、bk为第k 天在村庄购买水和食物的数量。

计算第n 天水和食物的剩余量Sn和Wn：

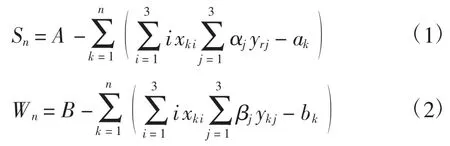
在时间递增的情况下，可运用式（1）、（2）不断更新玩家所处位置并计算下一天水和食物的保有量。

1.2 已知天气状态的最大资金剩余量模型

变量设置：f 表示剩余资金量；T 表示从起点到终点的历时天数，t 表示挖矿天数；其他设置同1.1 节。

目标函数为资金剩余量：

优化方向为max f。其中：f0=10 000 元为初始资金，c 为给定的挖矿基础收益，d=10 表示在村庄补充资源需支付基准价格2 倍的资金。

在问题一中，c=1 000 元/天。

根据游戏规则[1]设置约束条件：

体现资源不能耗尽。要求恰在终点处耗尽，即ST=WT=0，有利于最大化f max。

体现负重上限约束。初始时刻也受此约束，而达到3A+2B=1 200 可对f max 提供保障。

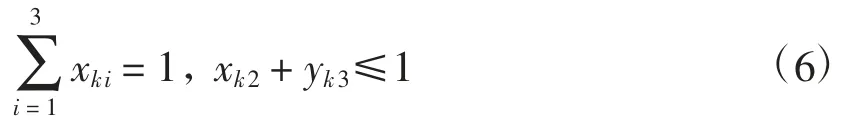
体现0-1 变量的单一选择性，以及沙暴天气不能行走。

体现所耗时间的限制。问题一中T0=30 天。

1.3 第一关的求解

30 天内天气状态已知[1]，玩家选择的行走状态分成3 种：停留、行走和挖矿。用动态规划求解第一关，需建立状态转移方程[2]。

方程中的变量解释：time 为时间，time-1 为前一时刻的时间状态，v 表示水与食物的质量，i 为水的消耗量，j 为食物的消耗量。Need 为消耗，_s表示水的属性，_w 表示食物属性，s′为增加的水质量，w′为增加的食物质量。下面分不同情况建立四维DP 状态转移方程。

第一种情况，天气不是沙暴时选择行走：

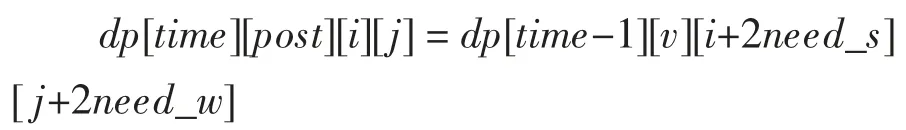
表示下一时刻的水与食物的消耗量在前一时刻水消耗量的基础上增加两倍基础消耗。

第二种情况，路过村庄时玩家选择补给水与食物：

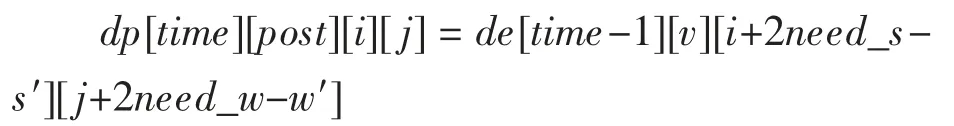
表示所耗资金为原先两倍，时间不增加。其中增加的补给量为负数，消耗量为正数。

第三种情况，路过矿山时，选择挖矿：

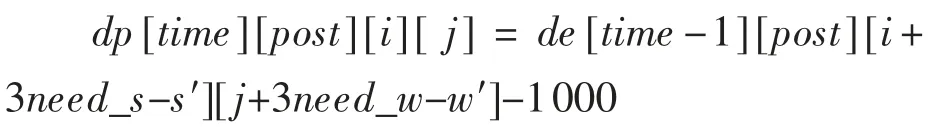
表示当天不能挖矿，下一状态停留在原地，并获基础收益。

第四种情况，停在原地：

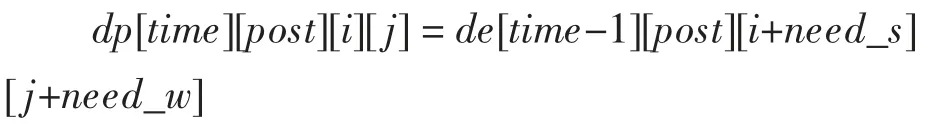
此时，只有一倍基础消耗，时间增加，位置不转移。

运用Java 进行编译，运算结果如表1 所示。最大资金剩余量为10 470 元。具体行走路径如图1 所示。

图1 第一关的具体路径

表1 第一关的部分运算结果

运算结果显示，玩家从出发到终点耗时24天。其中晴天出现7 次，6 次选择行走；高温天气出现12 次，5 次选择挖矿；沙暴天气出现5 次，其中1 次选择挖矿（沙暴天气必停，但可挖矿），4 次选择停留。

1.4 第二关的求解

第二关地图[1]的区域排列类似于矩形分布，从起点1 到矿山30 的最短路径需要走7 步。由相邻区域的交换律可知，固定步数时，7 块相邻区域等效，故可剔除以下属于冗杂多余的区域：

3，4，5，6，7，8，11，12，13，14，15，16，20，21，22，23，24，31，32。

起点到村庄需要8 步，故删除以下区域：

17，25，33，34，41，42，49，50，51，57，58，59。

村庄到终点删去绕行区域：40，48。

运用1.3 节的状态转移方程，代入目标函数，运用Java 进行编译，运算结果如表2 所示，最大资金剩余量为12 730 元。具体行走路径如图2所示。

图2 第二关的具体路径

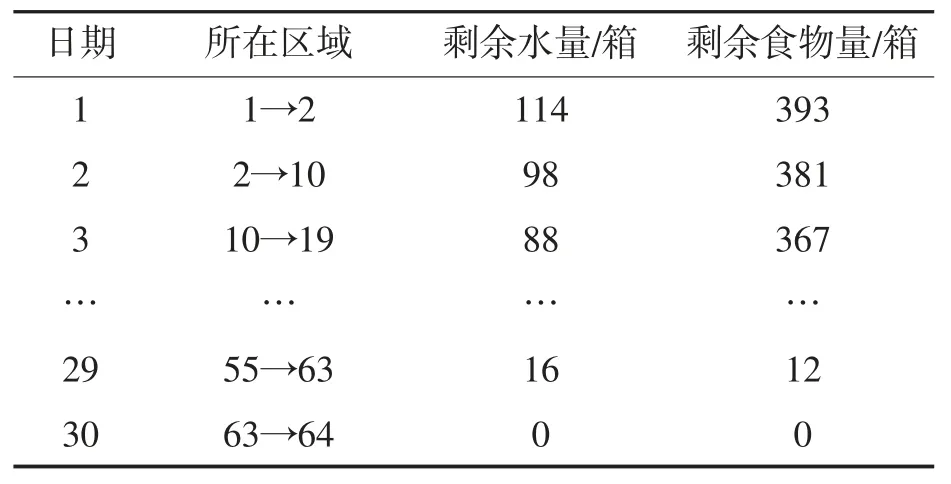
表2 第二关的部分运算结果

玩家的策略为：矿山较远，挖矿前要补资源，所以先到村庄，后到矿山。挖矿6 天折返回村庄又补资源，再经2 步到第二座矿山挖矿7 天，然后2步到达终点。

2 解决问题二的遗传算法

问题二包括第三关和第四关，玩家仅知道当天的天气状况，可据此决定当天的行动方案。

2.1 马尔科夫链天气预测模型

根据当天的天气状况，可利用马尔科夫链模型预测未来的天气状况。

以不出现沙暴的第三关[1]为例。设当天为晴天时，下一天是晴天和高温的概率分别为p 和1-p；当天为高温时，下一天是高温和晴天的概率分别为 p′和 1-p′，则称

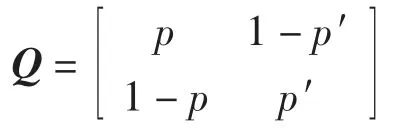
为一阶状态转移概率矩阵。其中的概率值满足0.1的梯度下降规则，即

若初始的状态概率分布为P0，则n 天后的状态概率分布为Pn=QnP0。当n 趋向于无穷时，Pn趋于恒定。这表明，用马尔科夫链对天气状态进行预测，与初始状态无关。

2.2 问题二的最大资金剩余量模型

问题二的优化模型与问题一相同，仍为式（1）～（7），只是部分已知参数有所不同[1]：第三关的挖矿基础收益为c=200 元/天，行走限时为T0=10天；第四关则仍为 c=1 000 元/天，T0=30 天。

此外，第三关的地图中有矿山但没有村庄，故只针对资金进行补充，不考虑资源补给，即所有的ak=bk=0；第三关不出现沙暴天气，所有yk3=0，涉及的下标仅取j=1，2 即可。

2.3 第三关的求解

先用Java 模拟出不同概率下设定的1 000 组数值解，多次尝试之后得出各种结果，再用遗传算法[3-4]，搜索出不同组中10 日天气情况不同的最优资金剩余量[5]。遗传算法的具体过程如下。

Step1：编码方案

行为状态的染色体个体为三进制串，以0、1、2分别表示停留、行走和挖矿。天气状态的染色体个体为二进制串，以0、1 分别表示晴天和高温。

Step2：种群初始化

随机生成1 000 组染色体，根据梯度下降原理，设定晴朗天气出现的概率为不同的p，高温天气则为对应的1-p。

具体以p=0.7 为例，利用马尔科夫预测模型[6-7]求解10 日内不同天气的数学期望。

Step3：初始群体的确定

种群规模N=1 000，交叉概率Pc=0.9，变异概率Pm=0.1，迭代次数m=1 000；

本文所选取的初始化群体为Java 在限定区间内随机模拟生成。按照这种解法，可以选出1 000 组个体组成解。

Step4：适应度函数

适应度函数即目标函数（3）。计算随机模拟的1 000 组天气状况下的最大资金保留量，计算每个个体的适应值Fitness 相当于通过自变量求得适应度函数的值，然后判断是否应删除质量差的个体。

Step5：约束检验

检验约束条件（4）～（7），剔除不合格的行为状态。

Step6：评价个体适应度

对不同组天气状态所生成的二进制串和人的行为方式进行解码处理，可得到不同天气状态下的表现型，由个体表现型计算对应个体的目标函数值。根据适应度函数最大的条件，求出个体适应度。

Step7：选择函数

运用最佳保留选择，随机概率设定为0.95。将当前种群中适应度最高的个体放到下一种群中。

Step8：个体的交叉与变异

从染色体串中选择NPc 个个体进行交叉选项，本文交叉方法为部分染色体段进行交叉，并检查交叉结果是否满足合法性，即在不同天气状态下玩家所对应的方式能否正确表示，若不符合则再次交叉或取消该操作。

Step9：循环

变异是根据变异概率更改染色体串中某个值使之变为不同天气状态和人的行为状态。

完成交叉变异后，代入适应度函数，选择再生个体，适应度高的个体即剩余资金留用数量高的被留下，一直进行循环。

Step10：终止计算

满足停止准则时终止计算，输出最优结果。

运用遗传算法进行具体运算[8]，设置初始晴天出现的概率为0.7。迭代1 000 次后最大资金剩余量为9 189，4 天的天气情况为“高温，高温，高温，晴朗”。

考虑是否要挖矿：挖矿需绕道两天，至少多付出 55×2×2 ＝220 元（晴天），而挖矿一天收益最多为200－55×3 ＝35 元（晴天），10 天中至多有5 天可以挖矿，获得收益的上限为35 × 5 ＝175元。由于收益小于付出，所以放弃挖矿。第三关的具体行走路径如图3 所示。

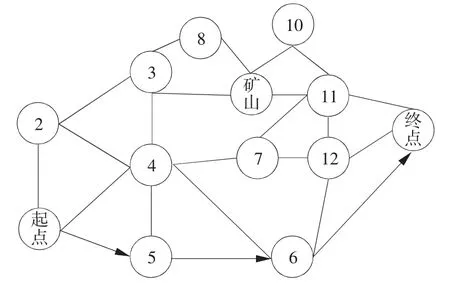
图3 第三关的具体路径

综上，一般情况下第三关玩家的最佳策略为：晴天必行走，出现高温则停留，若连续两天都是高温，则用马尔科夫链分析第三天的天气情况，经状态转移概率计算[9-10]，当第三天晴朗概率超过高温50 %时选择行走，否则继续停留。

2.4 第四关的求解

第四关既有矿山，也有村庄，且出现沙暴天气的概率较小[1]。求解方法与第三关相仿。

设置初始沙暴出现概率为0.1（较低值），运用Java 仿真模拟，沙暴出现的概率为0.1～0.4，依据收益的数学期望，经遗传算法求解，得到最大资金剩余量为1 1265 元，8 天的天气情况为“沙暴3天，晴朗 4 天，高温 1 天”。

分析求解结果，可得最佳策略：晴朗必走，出现高温适合停留，若连续出现高温天气，第一天选择停留，根据贝叶斯概率分布可得未来一天各种天气出现的概率，若出现高温天气的概率超过0.64 则停留，若低于0.64 则行走，遇沙暴时停留，有矿山则挖矿。