层次分析法在择偶问题中的应用研究

刘广会 叶丽丽 任朝

（1.白城师范学院，吉林 白城 137000；2.白城市洮北区民生中学，吉林 白城 137000）

一、确定择偶影响因素

由于选择合适配偶的情景设计要考虑的因素众多，因此在建立模型过程中，为增加实例研究结果准确性，设计《大学生择偶偏好调查问卷》，并对白城师范学院365 名同学进行了问卷调查，其中参与问卷调查的男性共94 人、女性共271 人。现以某一女性择偶为例，需从三名优质男性中挑选一位作为男朋友，根据现有择偶偏好研究及问卷调查结果（表1），以外貌特征、学历、财政收入、家庭背景、责任心为准则层，模拟三名男性基本情况（表2），并邀请测试者、婚介有经验者和心理学业界专家对三名男性的五项指标进行一对一比较，评价结果构造为成对比较矩阵。

表1 女性择偶偏好调查结果

表2 三名男性的基本情况

二、构造层次结构模型

从上述分析中，三个层次的要素也十分明显，最上层目标层为：最终挑选一位优质男性；中间准则层为：外貌特征、学历、财政收入、家庭背景、责任心；最下层方案层为：三名男性，构建层次结构模型如下。

三、构造成对比较矩阵

根据上述层次结构，采取1—9 比较尺度，构建准则层择偶影响因素相对于目标层的成对比较矩阵A，并将其根据（i,j= 1,2,...,n）按列归一化。

四、计算权向量并做一致性检验

用算术平均法求权向量，将A按列归一化后，按行求和，再将所求得和向量归一化，即可得准则层对目标层的权向量 w(2)。

求得矩阵最大特征根为

五、计算组合权向量并做组合一致性检验

在上述计算中，已求得准则层对目标层的权向量 w(2)。同样对待选择对象在各个择偶标准中的相对重要性进行判断，构建各个方案的成对比较矩阵，用B1,B2,B3,B4,B5分别表示P1,P2,P3对准则层外貌特征、学历、财政收入、家庭背景、责任心的优越性，可得：

对于每一个成对比较矩阵Bk,(k= 1,2,3,4,5)，都可以按照算术平均法（和积法）计算出权向量，分别记为，按照上述定义与公式可计算出方案层对目标层的每一个成对比较矩阵的最大特征根kλ(k= 1,2,3,4,5)、一致性指标CIk(k= 1,2,3,4,5)、一致性比率CRk(k= 1,2,3,4,5)，并对每一个成对比较矩阵做一致性检验（表3）。

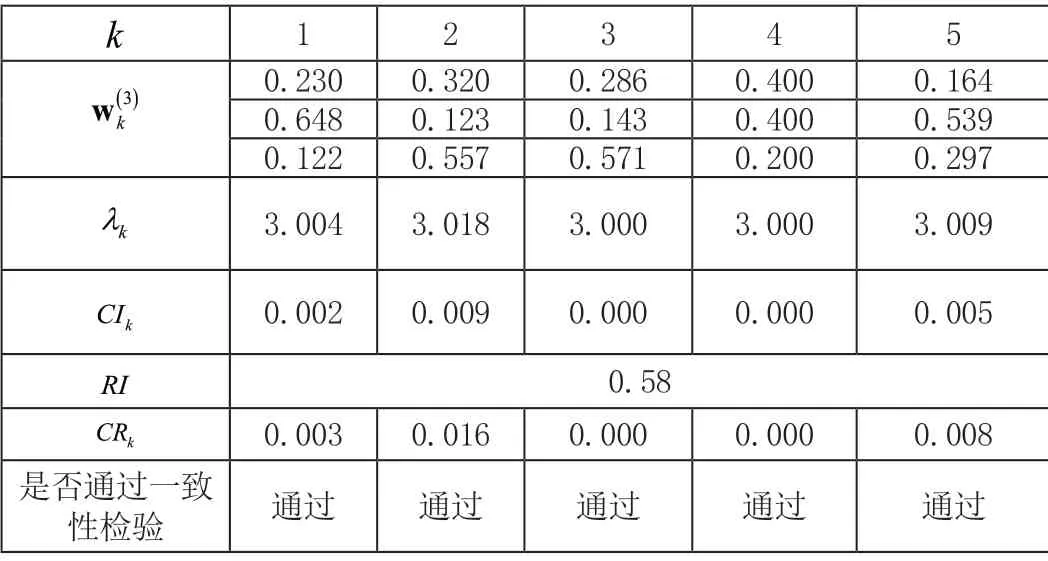
表3 第三层（方案层）计算结果

经计算，B1,B2,B3,B4,B5均通过一致性检验，证明所列比较矩阵符合标准。下面由准则层各个择偶影响因素对目标层的权向量w(2)和各个方案对各择偶影响因素的权向量，计算各个方案对目标层的组合权向量，称之为w(3)。

计算结果表明，三名男性所占的权重分别为：0.225，0.333，0.363。

下面对所求得的三位被选择男性对组合权向量一致性检验，以确定组合权向量是否可以作为最终的决策依据。

定义方案层的组合一致性指标为

定义方案层的组合随机一致性指标为

定义方案层对目标层的组合一致性比率为

CR=CR(2)+CR(3)= 0.009+0.005= 0.014 <0.1

组合一致性检验通过，所得组合权向量 w(3)可以作为最终决策的依据。

六、结果分析评价

择偶问题模型中准则层的影响因素确定是根据现有择偶偏好研究及择偶偏好调查结果所确定的，准则层与方案层对总目标的优先权重是根据被测试者以及婚介有经验者所列出的成对比较阵得出的，结果通过一致性检验具有可行性。

女性择偶实例最终首选方案是选择第三位男性。其中三位男性的权重分别为：0.225，0.333，0.363。由准则层权重计算结果不难看出，责任心是女性择偶最看重的，权重系数为0.405，其次是收入与学历，权重分别为0.253 与0.139，最后是家庭与外貌，权重为0.077 与0.048。由层次分析可知，测试者选择外貌较差、家庭背景一般，但责任心较强、收入与学历较高的男性的几率比较大。

从以上分析可以看出，利用层次分析法不但能够选出适合自己的配偶，而且还可以对各个配偶人选进行排序，定量分析与定性分析相结合，为择偶问题提供有效且可靠的依据，从而为当代青年建立稳定幸福家庭提供更具科学性的建议。

结论

本文利用层次分析法，最终发现在女性择偶过程中，责任心最重要的，其次是收入与学历，最后是家庭与外貌；在男性择偶过程中，责任心最重要的，其次是眼缘与工作能力，最后是外貌和学历。