基于有限元仿真的不同截面轨道炮特性分析
2021-11-17李海元栗保明
张 威,李海元,栗保明
(南京理工大学瞬态物理国家重点实验室,江苏 南京 210094)
1 引言
轨道炮是具有重大发展前景的新概念武器。轨道炮由一对平行金属导轨、电枢、弹丸、身管以及高功率脉冲电源组成[1]。身管结构是影响轨道炮性能的因素之一,选择合适的结构可以提高发射精度,减少炮膛损耗,增加轨道炮寿命以及可靠程度。在电枢高速状态下,轨道受到电磁力作用下产生瞬态变形,从而影响枢轨之间的电接触性能。国内外学者对轨道炮发射过程中轨道的受力与变形开展了研究。Tzeng[2]将弹性基础梁引入电磁发射装置轨道的力学模型中,给出了控制方程的数值解。张益男[3]求出了轨道在电磁力作用下横向变形的通解和内力的具体形式,同时分析了不同地基弹性系数对变形的影响。李鹤[4]指出了不同轨道截面的形状会对发射电流产生影响,从而抑制或者加重轨道的烧蚀。
目前国内外对轨道的振动或变形研究,大都基于将轨道视为施加了电磁力或电枢作用的弹性梁结构,重点计算电磁力或电枢作用中的一项,从而忽略了电枢与轨道之间的摩擦力。同时关于如何从结构上减少变形也少有论述。针对上述的不足,建立了身管-轨道-电枢模型,引入结构之间的摩擦力,同时考虑电枢与电流同时对轨道的作用,利用软件仿真计算,分析两种不同轨道发射时的身管反应,找出轨道结构影响身管变形的多种因素。
2 理论分析
轨道炮基本原理图如图1所示。

图1 轨道炮原理及坐标系示意图
轨道通电后,轨道附近产生磁场,电枢在磁场中受到安培力的作用,加速至离开轨道,发射过程完成。建立如图1所示坐标系,并以右上角标区分各构件:电流流入轨道为R+,流出轨道为R-,电枢为A。根据毕奥-萨伐尔定律[5]以及安培力法则,将所有通电区域分解为无数电流元,再积分各构件受到的电磁力。以单侧轨道受到的电磁力为例,电流流入轨道中任一点(XR+,YR+,ZR+),电枢内任一点(XA,YA,ZA)。该侧轨道受到电枢的电磁力为:
(1)
其中,μ0为真空磁导率;R为源点到场点的矢径,即(XR+-XA,YR+-YA,ZR+-ZA);J为体电流密度;电枢电流元体积dτA=dXAdYAdZA。
同理,对侧轨道对电流流入轨道的电磁力应为
(2)
在式(1)中,由于轨道的电流都集中在电枢后方,轨道Z坐标值必然小于电枢Z坐标值,故电枢对轨道的作用力始终向内(X方向)。而当电流存在速度趋肤效应以及大电流趋肤效应时,内侧轨道会聚集更多的电流,使轨道内侧电磁力比外侧更强。由于电枢产生的磁场在轨道区域具有X方向的分量,进而导致轨道受到不止一个方向的电磁力。同理,在式(2)中,两侧轨道X坐标值差恒负,所求轨道电磁力方向为X负方向;轨道间距离更近的点|R|较小,受到的电磁力更大。电磁力均具有图1示三个方向的分量,其中X方向为主方向;轨道受到的全部电磁力中,存在指向轨道内侧的电磁力。
3 模型构建
3.1 物理模型建立
根据问题需要,建立两种轨道炮的物理模型。图2(a)所示为方形轨道模型,轨道截面形状为正方形;图2(b)所示为圆形轨道,每一侧圆环内侧截面积与方形轨道相同。电枢均为C型电枢。轨道外侧为绝缘材料,绝缘材料外被封装身管包裹。两种轨道选取相同厚度0.1m,相同的枢轨接触面积0.01m2,相近的轨道横截面积0.01m2,进行对比实验。

3.2 模型参数
方形轨道为0.1m*0.1m*1.5m的长方体,单侧体积为0.015m3,电流法向横截面积0.01m2。圆形轨道为部分圆环,内径为0.056m,外径为0.112m,单侧体积为0.01575m3,电流法向横截面积约为0.01m2。
方形电枢取体积0.1m*0.1m*0.15m长方体,之后内侧剖去约为0.000414m3的体积,得到体积约为0.001086m3的C型电枢。圆形电枢取体积0.0562π *0.15 m3的圆柱体,在内侧剖去体积约为0.000487m3的几何体,得到最终体积约为0.001013m3的C型电枢。电枢放置在尾部距离轨道底部1m处。
封装身管均采用圆柱形中空身管,绝缘材料圆柱半径为0.3m,高1.5m,剖去内部轨道与电枢所需空间后,圆形轨道对应绝缘材料体积0.373m3;方形轨道为0.374m3。最外层钢套外径为0.33m,内径0.3m,高1.5m,体积为0.088m3。
3.3 材料模型
仿真计算需要为模型提供材料参数。材料选择:轨道材料采用某种导电性能良好的铜合金;电枢需采用较轨道更软的导电金属,选择某种较轻质铝合金;绝缘材料选择环氧树脂,具体参照论文[6],环氧树脂具有较高的强度,也有很强的绝缘能力;封装身管为不锈钢。计算需要的材料属性如下表:
4 电磁力仿真计算
根据上一章建立的模型,利用Maxwell3D进行电流-电磁体积力的模拟计算。
4.1 荷载施加
边界条件设置:利用真空圆柱体包裹整个轨道炮模型,真空环境磁导率为1,电导率0。轨道末端截面与真空圆柱体截面重合。在此时间节点取电流大小为150kA;电流从轨道一侧截面流入,经电枢后由另一端截面流出。电枢速度大小对电流趋肤效应的深度有影响[7-8],电枢设置为静止对本研究电流分布影响不大。电枢放置于轨道发射方向1m处。环境温度设置为22℃。
4.2 轨道整体体积力分布情况
①方形轨道体积力分布图
②圆形轨道体积力分布图
观察图3、5,轨道受到的电磁力基本上集中在电枢后段,电枢前段轨道无电流,电磁力迅速降为0;轨道在电枢翼端尾部的附近电磁力最大,说明电流在这个区域汇集。根据第一节的结论,不论哪一种轨道,其内侧受体积力总大于外侧。从图中色度变化分析,方形轨道从内到外的电磁力降幅更明显,从1.22*107降至3.48*106N/m3;而圆形轨道幅度较小,从1.06*107到5.3*106N/m3;此外,对比图4、图6电磁力矢量图,圆形轨道在小部分区域电磁力升至最高点,整体电磁力峰值高,达到2.38*107N/m3,但最高点附近电磁力快速下降,其它区域电磁力分布较为平均,基本包括7.9*106到5.3*106N/m3范围内;方形轨道主要工作区域范围内电磁力变化范围较大,其数值在1.2*107到8.6*106N/m3,这部分数值整体大于前者,但整根轨道峰值仅到1.56*107N/m3,低于前者。
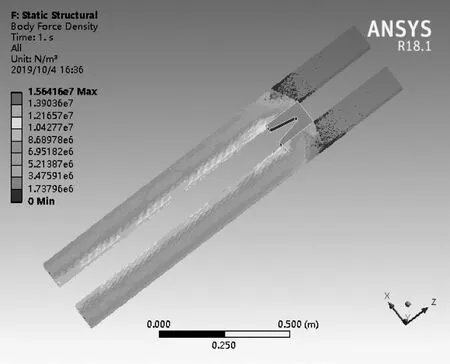
图3 方形轨道体积力分布情况图

图4 方形轨道体积力截面图

图5 圆形轨道体积力分布情况图

图6 圆形轨道体积力截面图
4.3 电枢整体体积力分布情况
将图7、图8对比,无论哪一种电枢,电流体积力都集中在两翼端前部连接处,这里的电流集中,电磁力较其它区域更大;方形电枢在这个区域电磁体积力在6.8*107到3.9*107N/m3范围内,少量区域电磁力水平逐渐升高至8.8*107N/m3;圆形电枢电流在集中处体积力在5.1*107到2.9*107N/m3范围内,同样也在部分区域电磁力升至6.6*107N/m3。电枢翼端方面,两种电枢电磁力在翼端尾部均逐渐减小,方形电枢电磁力逐渐减小到106N/m3便不再下降;而圆形电枢逐渐减小到0,通过输出全部大约46000个节点电磁力数据,发现其中约3%(1400个)电磁力为0,其余部分最低降至8*104N/m3。总体来看,方形电枢受到的总体积力合力在Z方向(发射方向)的值约为4542N,圆形电枢Z方向上的总合力约为4395N,圆形电枢推力略低3%。

图7 方形轨道电枢体积力分布图

图8 圆形轨道电枢体积力分布图
5 结构变形仿真计算
根据上一章得到的电磁体积力模型,建立结构-电磁耦合分析。
5.1 仿真环境设置
计算结构变形,首先设置材料属性。根据(表1)为各个构件设置材料属性。第二步设置接触类型,由于在静态模块下进行耦合,结构之间不能发生相对运动,同时结构之间也应存在摩擦力;设置摩擦类型为Rough,结构之间不发生相对滑动,结构间摩擦力可达到无限大。第三步按照1g/A的比例为电枢设置一定量的过盈接触,过盈量大小为2.4*10-7m,产生1500N的接触压力。第四步,为轨道与电枢导入电磁力,电枢位置与上一节相同。最后设置边界条件,将封装身管外层曲面设置为固定约束,即不发生变形,不产生位移;温度设在为22℃。分析算法选择Large Deflection大变形仿真,该算法包含非线性情况的仿真计算,对比线性算法可使结果更加精确。

表1 材料参数表
5.2 轨道变形情况
实际情况中,轨道变形具有三个方向的分量,其中影响枢轨接触的是X方向上的轨道形变;所示图中阴影部分为受外力变形前的状态,结构变形产生的偏移在图中表现有一定比例放大(放大2.5*104倍)。

图9 方形轨道变形云图
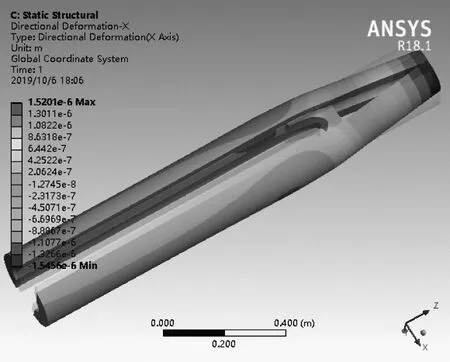
图10 圆形轨道变形云图
初步对比两种不同轨道的形变量,方形轨道最大值出现在电枢翼端附件,圆形轨道出现在轨道末端,圆形轨道最大值出现点并非轨道主要工作区域,但无论哪种轨道,其内侧形变量均大于外侧;在X方向上,轨道形变量最大值都在1.5*10-6m左右,两种轨道并无太大差别;从电枢翼端附近轨道来看,圆形轨道颜色更浅,推测形变量更小。
轨道沿发射方向,内侧轨道形变量平均值变化如图11。

图11 轨道内侧变形量
折线图表明,在电枢与轨道接触点以及轨道主要受电磁力影响的地方,圆形轨道的变形均低于方形轨道;在1.3m之后,圆形轨道产生了反向弯曲,而方形轨道则无限趋近原轨道位置。另外,不论是哪一种轨道,轨道扩张量最大的点都是出现在电枢后接近电枢的区域。总体上看,圆形轨道变化更加平稳。轨道主要的工作段在电枢附近以及轨道后方电流经过的地方。忽略圆形轨道前方收紧区域,取电枢位置(1m)处加上电枢长度(0.15m)处轨道的形变量,计算该区域形变量平均值,其中圆形轨道均值为9.90*10-7m,方形轨道为1.28*10-6m;圆形轨道形变量较方形轨道大约减少了23%。
5.3 轨道末端变形原因分析
上一节指出,圆形轨道末端产生收紧现象,而方形轨道则是趋近于原始轨道位置。为了探究原因,观测轨道在各个方向受到的应力的情况,发现在Z方向的正应力上,两种轨道产生了不同的应力表现,具体应力云图如图12。

图12 不同轨道应力对比图
所有云图经过处理,其中红色区域表示受到的正应力方向沿Z正方向,蓝色反之。可以明显看出,两种轨道受到的Z向正应力情况完全不同,在电枢前段,方形轨道内侧应力方向为正、外侧为负,而圆形轨道则完全相反;这就在两种轨道前端产生完全相反的力矩,其中方形轨道力矩向外且有其它结构阻止轨道向外扩张,圆形轨道力矩向内,轨道内部无阻挡;而在电枢后段,由于有电磁力的作用,轨道变形主要由电磁力控制。综上,由于轨道末端应力产生向内弯矩,使得圆形轨道末端向内收紧。
6 结果分析与讨论
1)圆形轨道在抗变形方面,效果优于方形轨道,相同发射条件下,截面形变量减少了23%。圆形轨道内侧受到的电磁力分布更加均匀、并处于较低范围,是轨道变形较为平缓的主要原因;方形轨道内侧轨道受电磁力均值较高,但峰值更低。
2)电枢推力上两种轨道无太大差别,说明发射效率方面,圆形轨道与电枢的组合不弱于方形轨道与电枢的组合。由于总体推力无差别,且方形电枢在对应区域电磁体积力高于圆形电枢(例如翼端、转角处),这说明方形电枢内部体积力下降更快,圆形电枢内部体积力更加均匀。另一方面,由于方形电枢内部小部分区域受到的电磁力远大于其它区域,施加更大电流则会放大这一缺陷,容易导致电枢局部变形过大而失效。从这一点看,圆形电枢应更适合大电流发射,在大电流发射情况下,电枢可以做到更小更轻,以减少寄生质量。
3)关于圆形轨道前段向内收紧的情况,由于设置模型时轨道只受到支持力与摩擦力;实际情况中,轨道由于变形也会压迫其它两个方向的包裹材料,进而有一个X方向的摩擦力抵抗向内的收紧。
总结:圆形轨道在主要接触方向上的变形小于方形轨道,可以提高轨道与电枢接触的稳定性,使得枢轨间紧密接触以减少放电烧蚀,提高轨道寿命。同时,电枢方面,圆形电枢对比方形电枢可以在不减少推力的情况下,使得电磁力分布更均匀,从此方面考虑圆形轨道更适合大电流发射。综上,圆形轨道结构可以减少由轨道的变形而失效的情况发生率。
