基于神经网络的布料机输送预报与仿真研究

周 鹏，郭菁菁，李 冬，于文达

(1.沈阳建筑大学科学技术研究院，辽宁 沈阳 110168；2.沈阳建筑大学交通工程学院，辽宁 沈阳 110168；3.沈阳建筑大学机械工程学院，辽宁 沈阳 110168)

1 引言

近年来，随着国家建筑产业的发展和技术的提升，装配式建筑成为建筑领域的发展热点。而混凝土预制构件是重要的装配式建筑品部件，其采用工业化生产方式。与现浇混凝土生产方式相比，在工厂中生产的预制混凝土构件具有安全、环保、耐用、可维护等诸多优点[1-3]，其需求量也越来越大。为提高预制购件的产量，大多数工厂选择购买国外的混凝土预制构件生产设备，这在很大程度上制约了我国高端装备制造业的发展和工程装备能力的提高，同时也增加了成本，成为我国预制装配建筑产业发展的瓶颈问题。因此，需要研发出适合我国国情的具有自主知识产权的混凝土预制构件生产设备。

螺旋式混凝土布料机是混凝土预制构件生产中的重要设备，目前主要采用人工控制方式进行布料生产[4-5]。面对预制混凝土构件生产方式的变革，原有混凝土布料机的人工控制方式已经无法满足产业发展需求，急需向自动化、信息化及智能化方向转变。

混凝土布料机螺旋输送量模型是实现自动化布料的重要模型，主要用于给出布料重量控制目标值，其计算精度直接决定布料重量控制系统的稳定性，也影响最终布料生产的构件重量精度。传统混凝土布料机螺旋输送量计算模型的很多参数均依靠经验确定，如物料堆积密度、填充系数等，导致现有模型输送量计算精度低，无法用于布料重量控制目标值的设定，进而也限制了产业升级进程。

人工神经网络方法可以高精度的逼近任意非线性函数，被广泛应用于模型预报[6]，如Yun S.W.等应用BP神经网络进行油藏预测，提高了油藏量预测的精度[7]；Islam Badar等应用BP神经网络进行非常短期的电能需求预测，取得了很好的效果[8]；Kamal U.A.等利用神经网络模型预测湖泊的水污染情况，结果表明神经网络模型的预测误差小于回归模型的预测误差[9]。上述应用案例为采用神经网络预报混凝土布料机螺旋输送量的可行性提供了有力支撑，为此，本文基于螺旋输送机理模型和BP神经网络基本原理，研究布料机的螺旋输送量智能预报方法，并通过实验对预报方法进行验证。

2 螺旋输送量机理预报模型

混凝土布料机分为摊铺式布料机和螺旋式布料机，与摊铺式布料机相比，螺旋布料机布料更精细，因此将对螺旋布料机输送量进行研究。螺旋布料机结构如图1所示。

图1 螺旋混凝土布料机结构图

在混凝土布料机输送混凝土的过程中，螺旋叶片在布料机布料口腔体中，通过旋转的方式不停推拨混凝土，使混凝土随着螺旋叶片上下翻滚，同时还会随着螺旋叶片的旋转沿轴向布料口出口方向运动，其单位时间内通过布料口出口横截面的混凝土体积即为螺旋输送量，行业内通常采用式(1)对螺旋输送量进行计算

Q=3600SρVz

(1)

式中：Q为布料机的螺旋输送量，S为螺杆中混凝土层的横截面积，m2；ρ为混凝土的堆积密度，t/m3；Vz为螺杆内混凝土的轴向输送速度，m/s。

料层横断面面积为

(2)

式中：D为螺旋叶片直径，m；d为螺旋轴直径，m；Ψ为填充系数；c为倾斜修正系数。

Vz按下式计算

(3)

式中：P为螺距，m；n为螺杆转速，r/min。

将式(2)和式(3)代入式(1)，得布料机螺旋输送量

Q=47ψPcnρ(D2-d2)

(4)

3 输送量BP神经网络预报建模

由于混凝土布料机的影响因素与输送量关系为非线性，而BP神经网络对非线性系统的预报效果很好，因此将采用BP神经网络进行布料机输送量的预报。BP神经网络分为信息的正向传播与误差的反向传播两个部分，本节将对这两个部分进行设计以实现输送量的智能预报。

3.1 输入信息的正向传递

BP神经网络读取布料机螺杆转速，螺距以及混凝土配比的输入数值后，按照正向传播方向，即依次经过输入层、隐含层和输出层的处理后，才能得出布料机输送量的预测值。所以，下面依次对此BP神经网络的输入层、隐含层和输出层进行设计。

1)输入层设计

输入层神经元个数对布料机输送量BP神经网络的稳定及预测准确度有重要影响，一般依据预测对象的影响因素来确定。

由螺旋输送量机理预报模型相关计算式(1)～(4)可知，布料机输送量的影响因素主要包括：摩擦系数、混凝土配比、填充系数、螺杆转速、螺距、螺杆外径和螺旋轴直径等。其中，摩擦系数与混凝土性质及螺杆材料有关，对于指定的混凝土布料机，其所采用材料是确定的，所以摩擦系数对布料机输送量影响主要由混凝土性质决定；因螺杆填充系数主要受螺杆转速和混凝土性质影响，所以可直接采用这两个因素代替螺杆填充系数计算布料机输送量[10]；因螺杆外径和内径相对于其它因素来说，对螺旋输送量影响明显偏小[11]，所以可忽略这两个因素对输送量的影响。综上，混凝土配比、螺杆转速和螺距这三个影响因素确定为布料机输送量BP神经网络的输入量，每个因素对应一个输入神经元。

为避免输入量物理单位不一致影响神经网络的预报效果，采用式(5)对螺距、螺杆转速和混凝土配比的值进行归一化处理

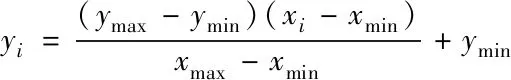
(5)

式中：xi为样本原始数据；xmin和xmax分别为所有数据中的最小值和最大值；ymin和ymax分别为输入数据规划范围的下限和上限，ymin=-1，ymax=1。

被归一化的输入数据被送入输入层神经元进行计算处理，输入层神经元计算采用logsig(log-sigmoid)作为传递函数，其传递函数计算式为

(6)

归一化后螺距、螺杆转速和混凝土配比分别为I1=[p1，p2，…，pn]，I2=[n1，n2，…，nn]，I3=[g1，g2，…，gn]，则输入层的输出为

(7)

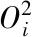
2)隐含层设计

隐含层设计包括隐含层的层数以及每层的神经元数的设计。据cybenko证明，拥有一层隐含层的神经网络即可逼近任何非线性函数[12]，所以布料机输送量BP神经网络的隐含层数选为1层。

对于隐含层神经元，其数量越多，不仅会使神经网络的函数映射越复杂，还会使网络收敛越慢、训练时间更长，甚至会导致神经网络出现过拟合，从而降低网络容错性。对于本文研究的螺旋输送系统，隐含不可避免的输送量影响因素还有螺杆的磨损b=[b1，b2，…，bn]，温度t=[t1，t2，…，tn]，螺杆振幅a=[a1，a2，…，an]等很多因素，它们之间的关系如式(8)所示

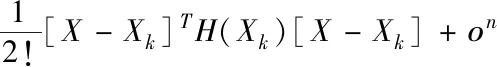
(8)

目前，隐含层神经元数量主要依据经验式(9)来计算

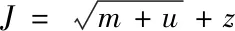
(9)

式中：J为隐含层神经元数；m为输入层神经元数；u为输出层神经元数；z为1～10之间的常数。

对于隐含层传递函数采用与输入层传递函数相同的形式，见式(10)所示，而其输出计算式为

i=1，2，3，j=1，2，…，J

(10)

2)输出层设计

因采用BP神经网络螺旋输送量模型预报的是布料机输送量，所以输出层神经元数量为1。输出层神经元的传递函数采用纯线性(purelin)函数，即采用式(11)来计算BP神经网络的螺旋输送量预报模型

(11)

式中：O为输出层神经元实际输出，wj为隐含层第j个神经元到输出层神经元的连接权值，其初始值通常也是随机产生，θ为输出层神经元的阈值。

3.2 误差的反向传播

BP神经网络采用误差反向传播方式调节各层权值，使网络输出值逐渐趋于目标值。具体做法是：求出输出节点误差，采用误差梯度下降法(trainlm)修正各层连接权值和阈值，由输出层到隐含层逐层修正，形成反向传播，经过多次反向传播修正，直至BP神经网络输出误差减少到指定目标精度范围内，输出最终预测结果。

1)输出层节点连接权值与阈值的修正

输出节点的均方误差为

(12)

式中，E为输出节点的均方误差；Ot为输出层神经元的期望输出，p为样本数。

均方误差对输出节点连接权值求导，得

(13)

E是多个Op的函数，各Op间相互独立。

设输出节点误差为δ=(Ot-O)，则

(14)

采用误差梯度下降法修正连接权值，则

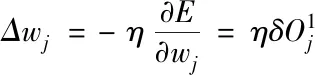
(15)

(16)

式中：η为学习速率，η∈(0，1)，k为训练步数。

均方误差对输出节点阈值求导，得

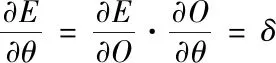
(17)

根据误差梯度下降法对阈值修正得

(18)

θ(k+1)=θ(k)+Δθ=θ(k)-ηδ

(19)

2)隐含层节点连接权值与阈值的修正

隐含层节点连接权值与阈值的修正方法与均方误差对隐含层节点连接权值求导，得

(20)

(21)

采用误差梯度下降法修正连接权值，则

(22)

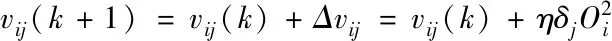
(23)

在对网络各层连接权值修正的同时，阈值也要被修正。均方误差对隐含层节点阈值求导

(24)

根据误差梯度下降法对隐含层阈值修正得

(25)

qj(k+1)=qj(k)+Δqj=qj(k)-ηδj

(26)

将修正后的连接权值和阈值代入式(10)和(11)并计算均方误差直至其小于0.001，输出布料机输送量的预测值。

综上，设计的三层BP神经网络螺旋输送量预报模型结构如图2所示，其输入层有3个神经元，它们对应的输入量依次为螺距、螺杆转速和混凝土配比，输出为布料机输送量。

图2 输送量BP神经网络结构

3.3 计算步骤

1)算法参数初始化。随机产生隐含层和输出层的阈值初始值、输入层到隐含层以及隐含层到输出层的连接权值初始值。

2)输入数据归一化处理。输入影响因素数据及其对应输出值构成的样本数据集，采用式(5)对样本输入数据进行归一化处理。

3)样本数据输入的正向传播计算。对样本输入影响因素，依次按照式(7)、(10)和(11)计算神经网络输出值，即螺旋输送量预报值。

4)误差计算与判断。按式(12)进行均方误差的计算，若均方误差小于目标误差，则将y=O代入式(5)，进行输出数据的反归一化处理，输出最终BP神经网络的输送量预报值；否则进行步骤5)，并重复步骤3)和4)。

5)连接权值和阈值的修正。按式(16)和(19)进行输出层连接权值和阈值计算，按式(23)和式(26)进行隐含层连接权值和阈值计算，并计算输送量。

图3 BP神经网络计算流程图

4 仿真研究

为验证布料机输送量BP神经网络预报模型的效果，对基于经验参数的传统螺旋输送量解析模型以及本文设计的布料机输送量BP神经网络预报模型进行仿真，并分析比较二者仿真效果。

为达到上述目的，首先对实验条件及样本数据的获取进行说明介绍；其次，对布料机输送量BP神经网络预报模型的结构参数进行调试优化；最后，进行实验对比并分析效果。

4.1 实验条件及样本数据获取

为实现后续BP神经网络螺旋输送量预报的仿真，需要样本数据和实验验证数据。由于预制构件厂的布料机体积大，很难准确对混凝土进行称重来评估布料机输送量BP神经网络的预报效果。因此按照容积5:1的比例对工厂布料机进行缩小，搭建了实验平台，使用PLC对螺杆转速等进行控制，并通过电子天平来测量布料机输送的混凝土重量。

实验平台的尺寸参数为：D=105mm，d=52mm，倾斜角度为0°。由倾斜角度及混凝土粒径查经验数据可确定螺杆修正系数c=1，填充率Ψ=0.3。

根据实验台参数，取螺距P=[90，100，105]mm，螺杆转速n=[15，30，50，60]r/min，以及四种行业内常用的混凝土配比。将以上三种因素的数据进行随机排列组合，取36组进行实验测出每组数据下不同的输送量值，作为样本数据。

从实验获得的36组数据中随机选择30组数据，用作BP神经网络的训练数据，剩余6组数据作为实验验证数据。并使用平均相对误差来表征预测误差。

4.2 BP神经网络结构参数调试优化

为使设计的BP神经网络螺旋输送量预报模型通过有限的训练达到较好的预报效果，分别对隐层神经元数量以及学习速度速率进行调试优化。

由第2节可知，本文设计BP神经网络螺旋输送量模型的输入层神经元数为3，输出层神经元数为1，代入式(7)可得隐含层神经元数范围区间为3～12。根据图2中建好的神经网络模型，固定学习速率为0.01，令隐含层神经元数J=[3，4，5，6，7，8，9，10，11，12]，使用随机选择的30组数据进行训练，剩余6组数据进行预测，逐个计算每个隐含层神经元数量对应的神经网络预测误差。所以每组仿真反复进行15次，记录15次仿真中最小的预测误差值，如表1所示。

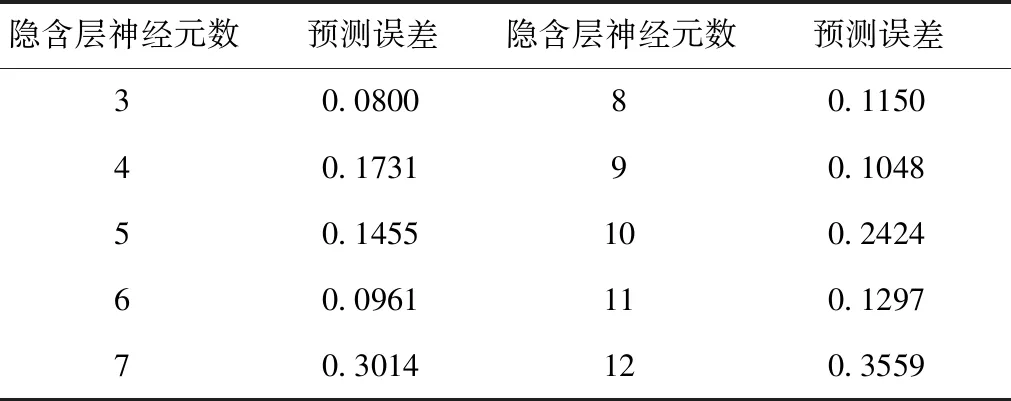
表1 不同隐含层神经元数下的预测效果

由表1中各个隐含层节点数量对应的预测误差可知，当隐含层节点数为3时，对应预测误差最小，所以，隐含层神经元数量确定为3。

在确定BP神经网络螺旋输送量预报模型的基础上，调试网络的学习速率，以提高神经网络在有限训练次数内的收敛速度及效果。学习速率一般采用试错法，其取值范围通常在0.001～0.8之间。为兼顾学习速率调节的快速性及效果，当其在0.001～0.01之间时，设置变化步长为0.001；当学习速率在0.1～0.8之间时，设置变化步长为0.01。根据图2中建好的神经网络模型，固定隐含层神经元数为3，使用随机选择的30组数据进行训练，剩余6组数据进行预测，逐个计算每个学习速率对应的神经网络预测误差。每组仿真反复进行15次，记录15次仿真中最小的且小于0.1的预测误差值，如表2所示。

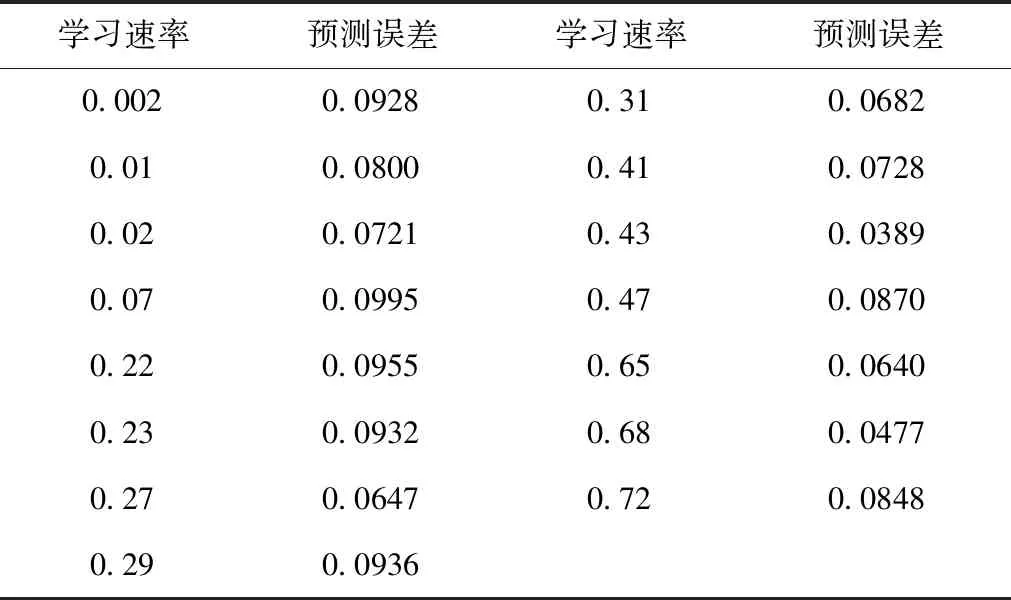
表2 不同学习速率下的预测效果

由表2知，当学习速率为0.43时预测误差为最小值，即0.0389，所以学习速率设置为0.43。

至此，布料机输送量BP神经网络模型参数已调试完成，对调试好的模型进行仿真，如图4所示。

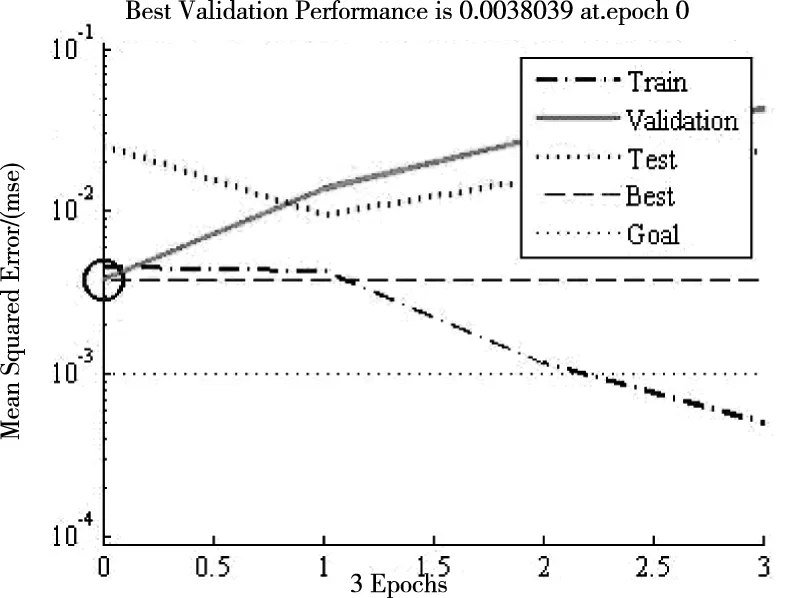
图4 仿真结果曲线

4.3 效果分析

采用剩余6组数据分别使用螺旋输送量机理预报模型式(4)和BP神经网络螺旋输送量预报模型进行预报，两个模型输出的预报结果与实际测量结果进行对比，如图5所示。螺旋输送量机理模型以及BP神经网络螺旋输送量模型预报值的平均相对误差如图6所示。

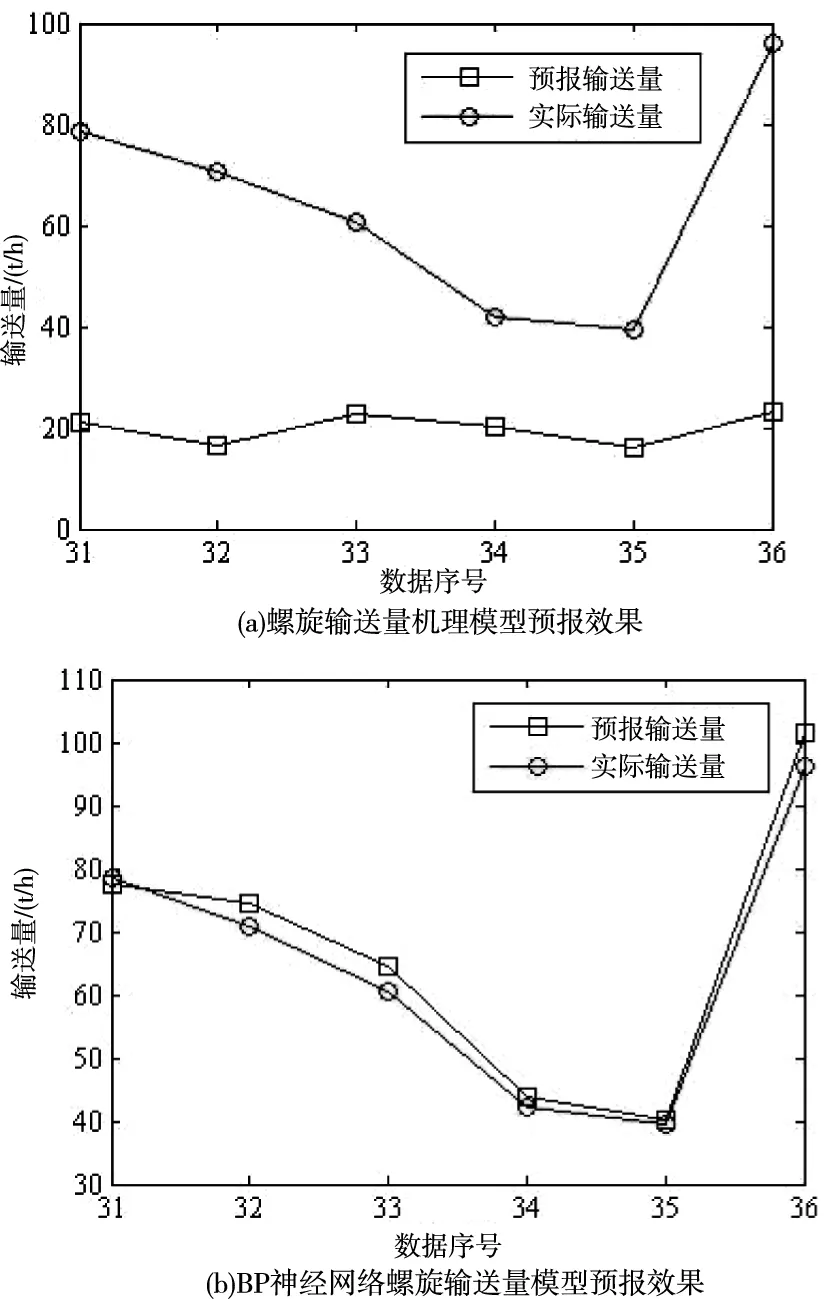
图5 螺旋输送量期望值与预报值对比效果图

图6 两种模型预报的平均相对误差对比图

从图5可以看出，BP神经网络螺旋输送量预报模型的预报值明显比螺旋输送量机理模型的计算值更接近实际输送量值。由图6可进一步看到，BP神经网络螺旋输送量预报模型的预测误差在0.0389附近波动；而机理预报模型的预测误差则波动较大。综上可知，基于BP神经网络的螺旋输送量模型预报精度明显高于基于经验数据的螺旋输送量机理预报模型，且预报值振幅小，计算结果更加稳定。

5 结论

预制构件混凝土布料机进行自动布料重量控制时，因基于经验值的螺旋输送量机理预报模型计算精度低，导致重量控制系统因缺少准确目标设定值而无法充分发挥其性能。为此，结合螺旋输送量预报机理，以输送物料性质、转速和螺距这三个主要影响因素为输入量，以螺旋输送量为输出，通过参数调试提出并建立了基于BP神经网络的螺旋输送量智能预报模型，其模型结构为3-3-1。在此基础上开展仿真，结果表明，与基于经验数据的螺旋输送量机理模型计算数据相比，基于BP神经网络的螺旋输送量预报精度高，且计算结果平稳性好，不会出现过大振动，体现出良好的准确性和稳定性，可用于混凝土布料重量自动控制系统目标值的设定，为预制混凝土构件重量的自动化和智能化控制奠定基础。