基于非线性空间及空间约束的遥感图像配准

王亚丽，赖惠成

(新疆大学信息科学与工程学院，新疆乌鲁木齐830046)

1 引言

图像配准[1]是将同一场景的不同时间，不同传感器或不同视点的两个或多个图像匹配[2]的过程[1]。它是许多遥感任务不可或缺的部分，例如变化检测，图像融合和环境监测等。基于特征的算法对图像灰度变化和遮挡具有较好的稳定性[2]，并且目前在遥感图像配准中使用最多，尺度不变特征变换(SIFT)[3]是经典方法。但是，对于遥感图像，由于非线性强度映射的显着差异，正确对应的数量不足以确认匹配精度[4]。为了克服这个问题，Kupfer等人[5]提出了一种快速模式搜索SIFT(MS-SIFT)算法，联合了特征点的尺度，方向和位置信息。Gong.M等人[6]提出了基于SIFT和互信息的由粗到精的图像配准算法。然而，这些方法仍然无法对齐具有大灰度差异的遥感图像对。闻等人[7]提出了增强特征匹配方法(PSO-SIFT)，匹配性能得到明显改善，但是使用高斯尺度空间，容易使边缘和细节变得模糊，导致特征点定位精度差，特征描述子区别度低。李[8]将非线性扩散技术应用在多光谱图像配准中，实验也表明非线性扩散滤波能够增加特征点检测和配准精度，然而该算法用加性算子分裂(AOS)方案[9]求解非线性方程的解析解，AOS方案需要在每个时间步骤求解大型线性方程组，比较耗时。

对此，本文提出了基于非线性尺度空间的改进SIFT遥感图像配准算法，用非线性扩散方程和快速显式扩散方法(FED)[10]构建空间，其优势在于保留了尺度空间图像的边缘和细节，同时提高了速率；改进的梯度计算方法克服了遥感图像的非线性强度差异问题；建立空间约束，改善了配准结果，使配准结果更精确。

2 SIFT算法[3]原理

2.1 特征点提取

首先高斯函数建立尺度空间并通过其相邻尺度之间的差与图像卷积建立高斯差分尺度空间，用作高斯拉普拉斯算子的近似。高斯差分尺度空间定义为

D(x，y，σ)=(G(x，y，kσ)-G(x，y，σ))*I(x，y)

(1)

其中k是常量，表示相邻尺度空间的倍数，在SIFT算法中常取值为21/3。然后与三维中的26个点比较，选择局部极值点作为候选关键点。用拟合三维二次函数精确候选特征点的位置与尺度，并且删除低对比度的候选特征点。

2.2 特征点描述

利用图像的梯度直方图，来确定每个关键点的主方向。像素的梯度幅度与梯度方向定义为

(2)

(3)

L表示特征点高斯尺度空间图像，然后，将坐标轴旋转为特征点的方向，旋转后以主方向为中心取8*8像素的领域，将其分成16个子块，并计算每个子块8方向的梯度幅值，形成128维的描述符。

2.3 特征点匹配

使用描述符上的最小欧几里德距离作为关键点匹配标准，有关SIFT的更多细节可以在文献[3]中找到。

3 本文算法

基于非线性尺度空间和改进SIFT的遥感图像配准主要包括以下几方面改进：

1)用非线性扩散方程和快速显式扩散方程构建非线性尺度空间。

2)用各向同性Sobel算子计算尺度空间中以及在求描述符过程中涉及到的梯度信息。

3)构建空间约束条件，包括点和线。

算法整体流程如图1所。

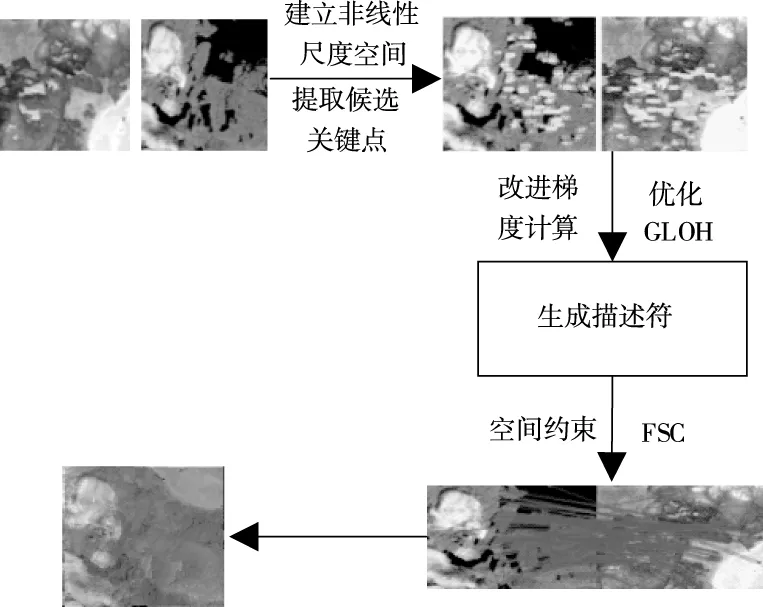
图1 配准流程图

3.1 构建非线性尺度空间

Nuevo等人[10]提出了一种快速多尺度特征检测和描述算法A-KAZE.该算法使用非线性扩散滤波器和快速显式扩散方程建立非线性尺度空间。

非线性扩散方程是

(4)

其中t是比例参数;div是散度操作符;∇表示梯度操作符c(x，y，t)是扩散系数，定义为

c(x，y，t)=g(|∇Lσ(x，y，t)|)

(5)

其中∇Lσ是高斯平滑后图像的梯度，g定义为

(6)

参数k是控制扩散水平的对比因子，确定必须保持或取消哪些边缘。它越大，保留的边缘信息越少。k值可以根据经验固定或从图像梯度直方图估计[11]，本文取k的经验值为梯度幅度统计直方图的70%百分位所对应的值。

由于非线性扩散方程(1)没有解析解，A-KAZE算法使用快速显式扩散(FED)算法获得近似解，并构建金字塔图像。使用FED算法对方程(1)离散化可以表示为

(7)

这里，A(Li)表示编码图像电导率的图像，τ表示时间步长，Li+1是根据前一级解决方案计算的，如下

Li+1=(I+τA(Li))Li

(8)

这里I表示单位矩阵，考虑到先验估计Li+1，0=Li，获得FED的周期为

Li+1，j+1=(I+τjA(Li))Li+1，j

j=0，……n-1

(9)

这里n表示显式扩散步骤的总数，τj代表相应的可变步长，如下

(10)

这里τmax是最大步长，不违反显式方案的稳定性条件更多细节可以在文献[10]中找到。

建立非线性尺度空间同SIFT算法类似，将非线性尺度空间离散化为O组，每组S层。定义空间中每层的图像尺度

σi(o，s)=σ02i+j/s;o∈[0，…O-1]，

s∈[0，…S-1]，i∈[0，…W-1]

(11)

其中σ0表示非线性尺度空间中第一组第一层图像的尺度，这里将其设置为1.6。W是平滑图像的总数;o和s分别是组数O和层数S的索引。值得注意的是，这里对图像要进行下采样，且一旦生成不同尺度的平滑图像，就执行相邻尺度之间的差异，然后同原SIFT一样提取候选关键点与精确定位。由于非线性扩散方程是按时间定义的，因此有必要将比例值转换为时间值，转换公式为

(12)

3.2 改进的梯度计算方法

在构建非线性尺度空间时，需要计算图像的梯度，一般可以通过一阶差分方法获得。然而，由于非线性强度映射的显着差异，正确对应的数量不足以确认匹配精度，因此，各向同性Sobel算子用于计算梯度的大小和方向，以改善描述符的灰度鲁棒性。首先由改进Sobel算子对图像L(x，y)进行卷积得到

Rx=H*L(x，y)，Ry=H′*L(x，y)

(13)

(14)

(15)

(16)

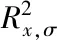
(17)

该算法优化了GLOH并生成新的特征描述符[12]。使用圆形邻域和对数极坐标生成特征描述符。根据关键点所在图像尺度σ对各圆环半径进行自适应调整，描述子中最大圆环半径R1为12σ，R2和R1的比值为0.73，R3和R1的比值为0.25，梯度方向在八个区间中量化，最后特征描述子为136维。

3.3 空间约束条件

首先初匹配用最近邻与次近邻比值法，并且距离比阈值dratio设置为0.9。然后通过快速抽样一致性(FSC)算法[13]计算初始变换参数，然后从两个角度构建空间约束条件。

1)点约束

正确的对应关键点应位于相应图像中的相同位置[14]。考虑到点坐标不可避免的误差，每个正确对应点之间的偏差误差应足够小。由文献[7]启示，定义位置欧式距离

PED(i)=(1+ep(i))ED(i)

(18)

其中ED(i)表示对应于关键点描述符的欧几里德距离。位置转换模型误差ep(i)定义为

(19)

其中T((x′i，y′i)，μ)是相似变换模型，μ是转换模型参数。

2)线约束

如果某匹配对是一对正确的匹配对，则该匹配对与其它点距离的比值应该不变，如图2所示，这称为距离比不变标准。在实验中，距离比不变准则用于得到最精确的结果。

(20)

这些空间约束逐一前进，逐渐缩小范围，最终得到确切的结果。最后用快速抽样一致性算法(FSC)算法从关键对中找到正确的对应关系完成图像配准。

图2 两个图像之间的空间约束

4 仿真校验与分析

4.1 测试数据

为了评估所提出的方法，测试了四组图像对。这些图像对如图3所示。第一对是来自美国地质调查项目的多光谱图像[7]，Lat /Long：69.6 /-92.7，240-m分辨率。选择来自波段5(传感器：Landsat-7 ETM+，日期：2000/7/24)的尺寸为614×611的区段作为参考图像。为了增加测试数据集的难度，在模拟旋转90°之后，选择来自第3频段(传感器：Landsat 4-5 TM，日期：1999/6/28)的尺寸为614×611的片段作为感觉到的形象。第二对是像素为617×593多光谱遥感图像对，其中参考图像是Landsat-7 ETM卫星于2004年4月12日提取的第三波段图像。待配准的图像是由Landsat 4-5 TM卫星于2006年6月15日提取的第五个波段图像。第三组图像来自巴西的256×256的遥感图像对，其中参考图像是SPOT传感器于1995年8月8日提取的第3波段图像，待配准的图像是1994年6月7日由TM传感器提取的第4波段图像。第四组图像是一对像素为600×500的SAR图像。

图3 遥感图像测试对

4.2 评估标准

1)匹配准确度：用相应匹配关键点之间的均方根误差(RMSE)[7]来定量评估配准性能，它可以表示为

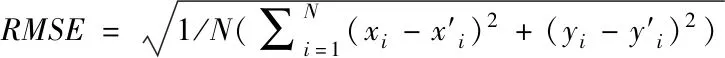
(21)

其中，(xi-yi)和(yi-y′i)是第i个匹配点的坐标，N代表匹配点的总数。

2)正确匹配的关键点数量[7]：由于提出的方法基于关键点，因此稳健性在很大程度上取决于关键点的数量。所以将正确匹配的关键点数量被用作评估所提出方法的稳健性的标准。因此当两种算法的RMSE彼此接近时，可以使用正确匹配的关键点数量进行进一步比较。

4.3 实验结果与分析

图4给出了非线性尺度空间和高斯尺度空间的简要比较，其中图4(a)是原始图像，图4(b)由高斯方程产生，图4(c)为非线性扩散方程产生，二者具有相同的比例。非线性尺度空间和高斯尺度空间之间的差异是显而易见的。随着尺度值的增加，高斯尺度图像变得越来越模糊，降低了特征点的定位精度，而非线性尺度图像具有相对轻微的模糊性，有助于提取更多关键点。

图4 高斯尺度与非线性尺度空间对比图

表1，表2，表3以及表4中分表显示了四组组测试图像对本文算法与SIFT算法[3]，SAR-SIFT[12]算法和PSO-SIFT[7]算法在匹配精度，正确匹配的关键点数和平均运行时间方面的实验比较结果。算法都在MATLAB R2016a下采用Intel core 3.20GHz处理器和8GB物理内存实现。注意，该算法执行十次，十个运行时间的平均值作为最终运行时间，*表示配准失败(RMSE>4)。

表1 第一组图像算法的比较

表2 第二组图像算法的比较

表3 第三组图像算法的比较

表4 第四组图像算法的比较

前三组测试图像对都是在不同的频带和不同的传感器设备中获取的，由于光谱带不同，遥感图像对之间存在一些不规则的强度映射关系。SIFT，SAR-SIF算法未能准确对齐三组测试图像对，PSO-SIFT算法可以精确配准三组测试对，但是PSO-SIFT算法与本文算法相比，在均方根误差相差不大的情况下，本文算法的正确匹配点对数远多于PSO-SIFT算法。可以看出本文算法可以准确配准具有不规则强度映射关系的多光谱遥感图像，也证明本文算法在配准性能上的优越性。

第四组测试图像对是一组SAR图像，SAR-SIFT算法是针对SAR图像提出的算法，具有一定的优越性，但是本文算法在正确匹配点对数上远超于SAR-SIFT算法，证明了本文算法可以准确配准SAR图像，也证明了本文算法对遥感图像配准的广泛性。

为了证明空间约束条件可以提高配准精度，改善配准性能，将有空间约束条件与未加空间约束的算法进行对比，如上表所示，构建约束条件后，获得了更多正确的匹配关键点数，均方根误差降低，对准精度提高。

图4显示了本文算法与PSO-SIFT算法特征点匹配的结果对比图，图4 (a)(c)(e)为PSO-SIFT算法在前三组测试图上匹配的结果，图4 (b)(d)(f)为本文算法的前三组测试图的匹配结果，可以看出本文算法的匹配效果明显优于PSO-SIFT算法。图4 (g)为SAR-SIFT算法对第四组图像的匹配结果，图4 (h)为本文算法对第四组图像的匹配结果图，可以看出本文算法对SAR图像的配准也有一定的改善。图6显示了所提出算法的棋盘式配准图像，可以看出两个图像的边缘以及区域都可以精确重叠，因此从直观方面可以判断配准结果是精确的，也再次证明提出的算法的准确性以及有效性。

图5 本文算法与PSO-SIFT算法以及SAR-SIFT算法匹配结果对比图

图6 棋盘拼接结果图

5 总结

本文为了实现遥感图像的精确配准，提高非线性灰度的鲁棒性，提出了基于非线性尺度空间的改进SIFT遥感图像配准方法。实验结果表明：①用非线性扩散方程和快速显式扩散方程生成遥感图像的多尺度表示，避免了高斯尺度空间的边界模糊，同时提高特征点定位精度；②用各向同性Sobel算子计算梯度幅值和方向，基于优化的GLOH生成特征描述符，克服了遥感图像对之间不规则以及复杂的强度变换关系，增加了正确匹配点对个数；③利用空间约束获得了更多正确的匹配关键点数和更高的对准精度。与现有技术方法相比，所提出的方法，配准性能得到明显改善。